红黑树的介绍与实现
前言
前面我们介绍了AVL树,AVL树是一棵非常自律的树,有着严格的高度可控制!但是正它的自律给他带来了另一个问题,即虽然他的查找效率很高,但是插入和删除由于旋转而导致效率没有那么高。我们上一期的结尾说过经常修改的话就不太适合AVL树了,而红黑树更加适合!OK,本期就来介绍一下赫赫有名的红黑树!
本期内容介绍
什么是红黑树
红黑树的实现
红黑树的效率分析以及应用
什么是红黑树?
红黑树是1972年由Rudolf Bayer发明的,当时被称为平衡二叉B树(symmetric binary B-trees)。后来,在1978年被 Leo J. Guibas 和 Robert Sedgewick 修改为如今的 " 红黑树 "。
红黑树是一种二叉搜索树,但在每个结点上增加了一个存储位表示结点的颜色,可以是红色或是黑色;通过对任何一条从根到叶子的路径上各个结点着色方式的限制,红黑树确保没有一条路径比其他的路径长出两倍,因而是接近平衡的!
OK,这就是一棵红黑树:
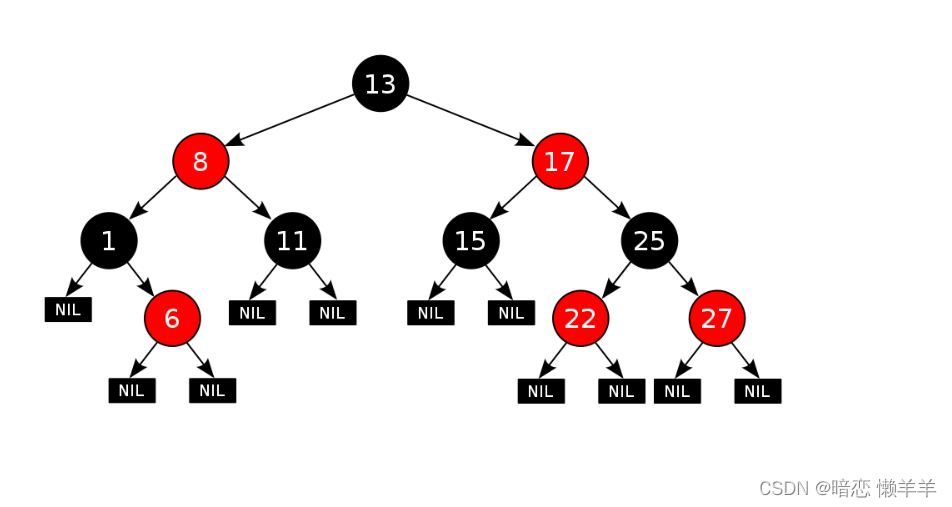
最长节点的路径就是一黑一红的交替,最短的就是两黑:
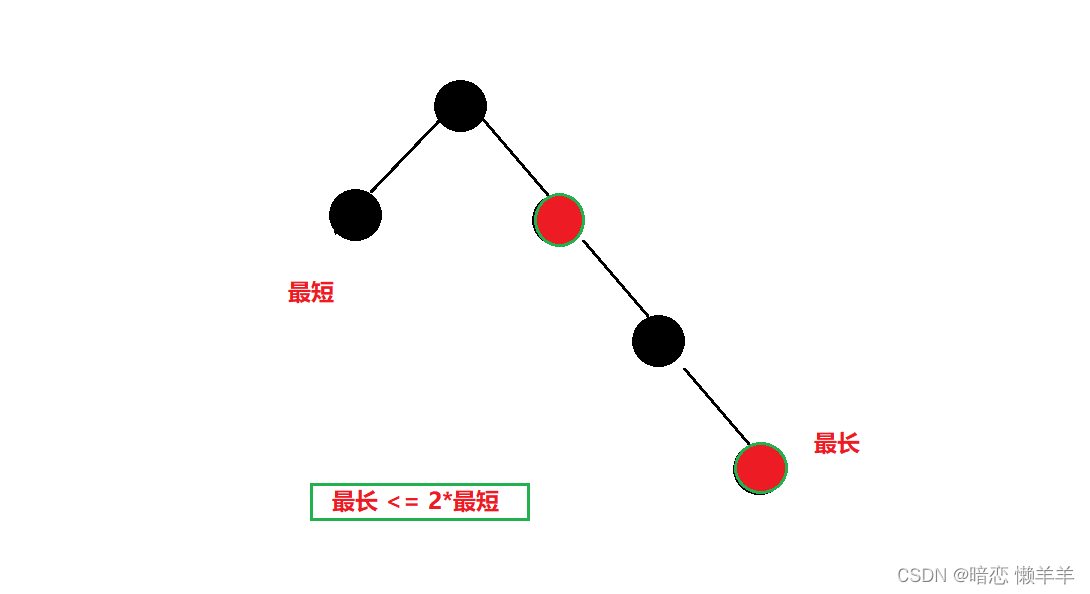
红黑树的性质
1、每个结点要么是红色,要么是黑色
2、根节点是黑色
3、如果一个结点是红色,则它的两个孩子结点是黑色
4、对于任意一个节点,从该结点到其所有的后代叶子结点的简单路径上,均包含相同的黑色结点
5、每个叶子结点就是黑色的(此处的叶子结点指的是空节点)
上面的这5条性质就是限制红黑树平衡的规则!其中4最重要的下来是3,基本所有的操作都是围着4进行的!!!
红黑树的实现
OK,上面介绍了红黑树是一种二叉搜索树,只不过是在每个结点添加了一个存储颜色的颜色位,所以它的大框架还是和搜索树一样的,所以我们就先搭一个框架出来!
enum Col//颜色
{RED,BLACK
};template<class K, class V>
struct RBTreeNode
{RBTreeNode<K, V>* _left;//左孩子RBTreeNode<K, V>* _right;//右孩子RBTreeNode<K, V>* _parent;//父结点pair<K, V> _kv;//数据域Col _col;//颜色RBTreeNode(const pair<K,V>& kv):_left(nullptr),_right(nullptr),_parent(nullptr),_kv(kv),_col(RED)//新插入的节点默认是红色{}
};template<class K, class V>
class RBTree
{typedef RBTreeNode<K, V> Node;
public:RBTree():_root(nullptr),_size(0){}private:Node* _root;//根节点size_t _size;//节点的数量
};思考:新插入的节点应该是红色还是黑色?为什么?
新插入的节点一定是红色!
因为新插入的节点是红色可能违反性质3,但一定不违反性质4!
如果新插入的是黑色,一定违反性质4,也就是在部分子路径上增加了黑色节点。所以插入的新节点一定是红色,即使红色违反了性质3也是比较好控制的!
OK,这里依旧是采用的三叉链,原因是方便找父亲:
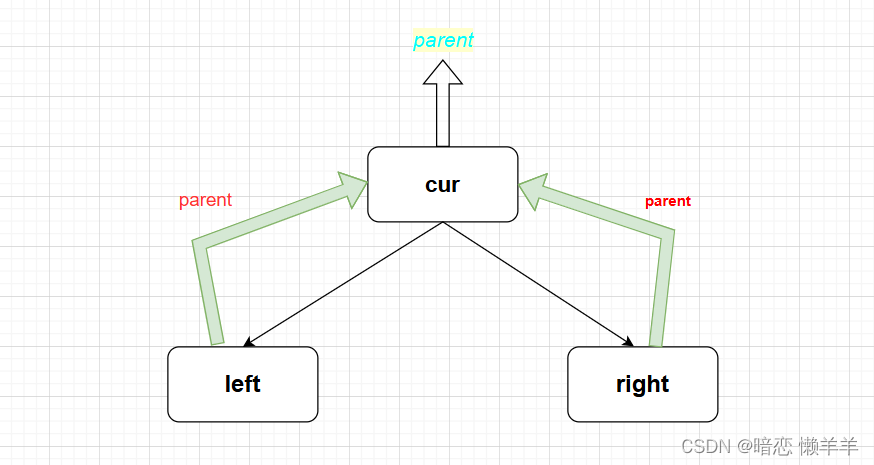
红黑树的插入
上面介绍了,红黑树的本质是一种二叉搜索树,所以先不管它的颜色和高度如何调节,先把搜索树的那一套给整出来:
bool Insert(const pair<K, V>& kv)
{Node* cur = _root;//当前节点Node* parent = nullptr;//插入位置的父亲//第一次插入if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;//根节点是黑色return true;}//寻找插入的位置while (cur){if (cur->_kv.first < kv.first)//插入节点的key比当前节点的key大{parent = cur;cur = cur->_right;//去右边找}else if(cur->_kv.first > kv.first)//插入节点的key比当前节点的key小{parent = cur;cur = cur->_left;//去左边找}else{return false;//插入的节点存在}}//找到插入位置cur = new Node(kv);//链接if (parent->_kv.first > cur->_kv.first){parent->_left = cur;}else{parent->_right = cur;}cur->_parent = parent;//颜色和高度调整//....return true;
}OK,还是先来验证一下当前的逻辑对不对,所以走个中序看看是不是有序即可:由于中序要根节点,而类外面是无法访问的,所以我们还是和以前一样搞成子函数或提供get和set方法;这里就搞成子函数了:
中序遍历
void _InOrder(Node* root)
{if (root == nullptr)return;_InOrder(root->_left);cout << root->_kv.first << ":" << root->_kv.second << endl;_InOrder(root->_right);
}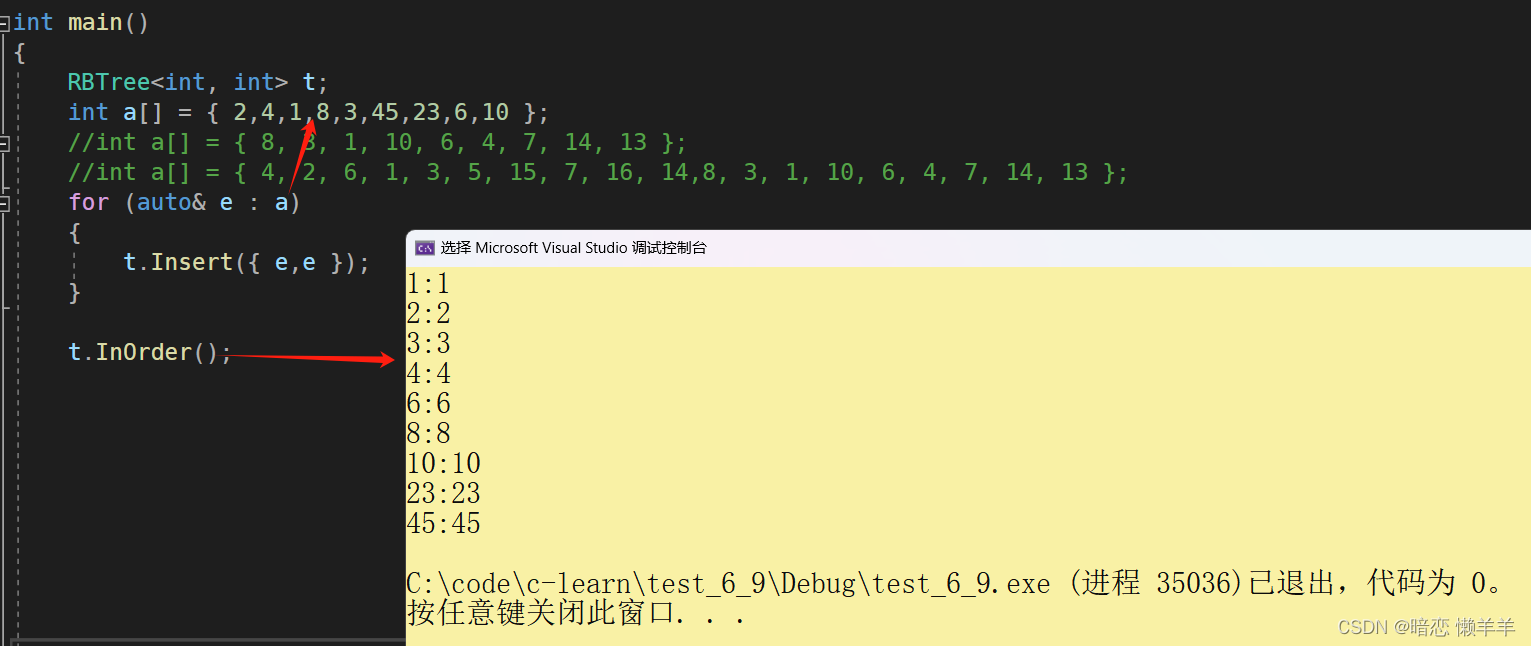
OK,没问题,下面我们就来讨论一下红黑树的维持平衡的方式:变色和旋转!
红黑树的变色和旋转
由于新插入的节点一定是红色的,此时分为两种情况,1、父亲为黑 2、父亲为红
如果父亲为黑,不违反任何性质,插入结束;
如果父亲为红,看看叔叔,此时叔叔有三类情况:1、叔叔存在且为红 2、叔叔不存在 3、叔叔存在为黑
如果,叔叔存在且为红:变色(将父亲和叔叔变黑色,将爷爷变红色),继续更新
如果,叔叔不存在或存在且为黑,旋转 + 变色(如果孩子是父亲的左/右,先对孩子父亲进行左/右旋,在对爷爷进行左/右)
OK,这里看着可能会有些迷,看看下面的导图会很清楚:
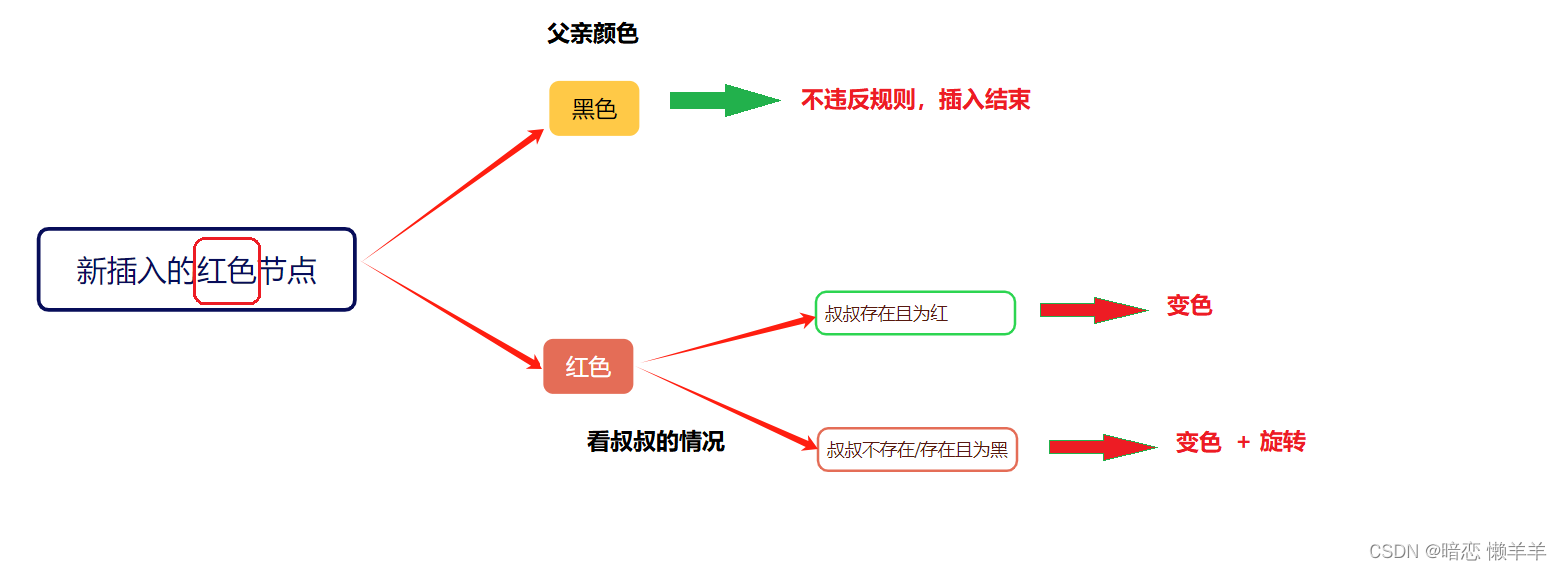
OK,理解了上述的表达,下面我来画图解释一下:
parent是黑色插入结束
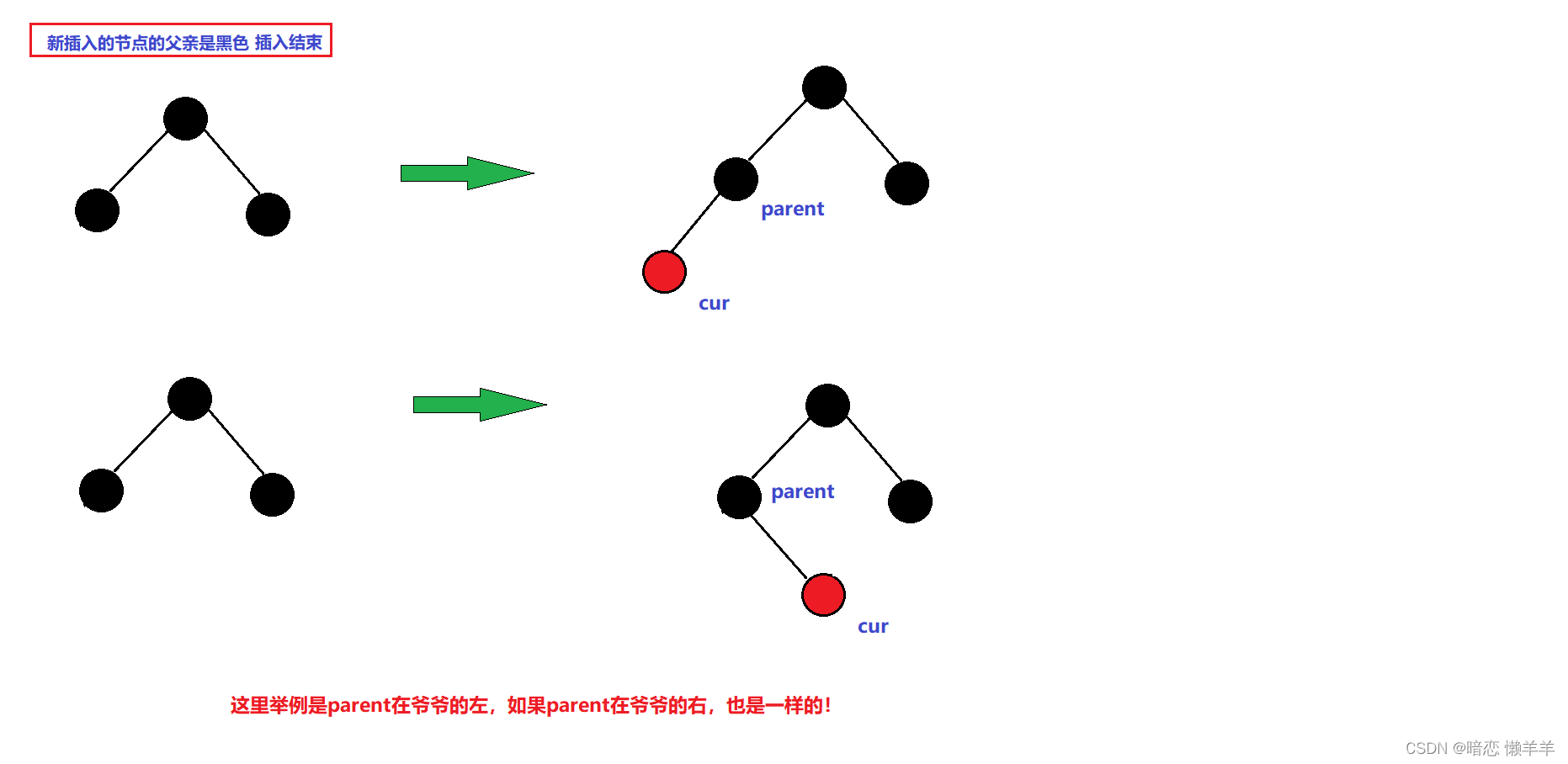
parent为红,叔叔存在且为红(变色)
父亲和叔叔变黑,爷爷变红,继续向上更新
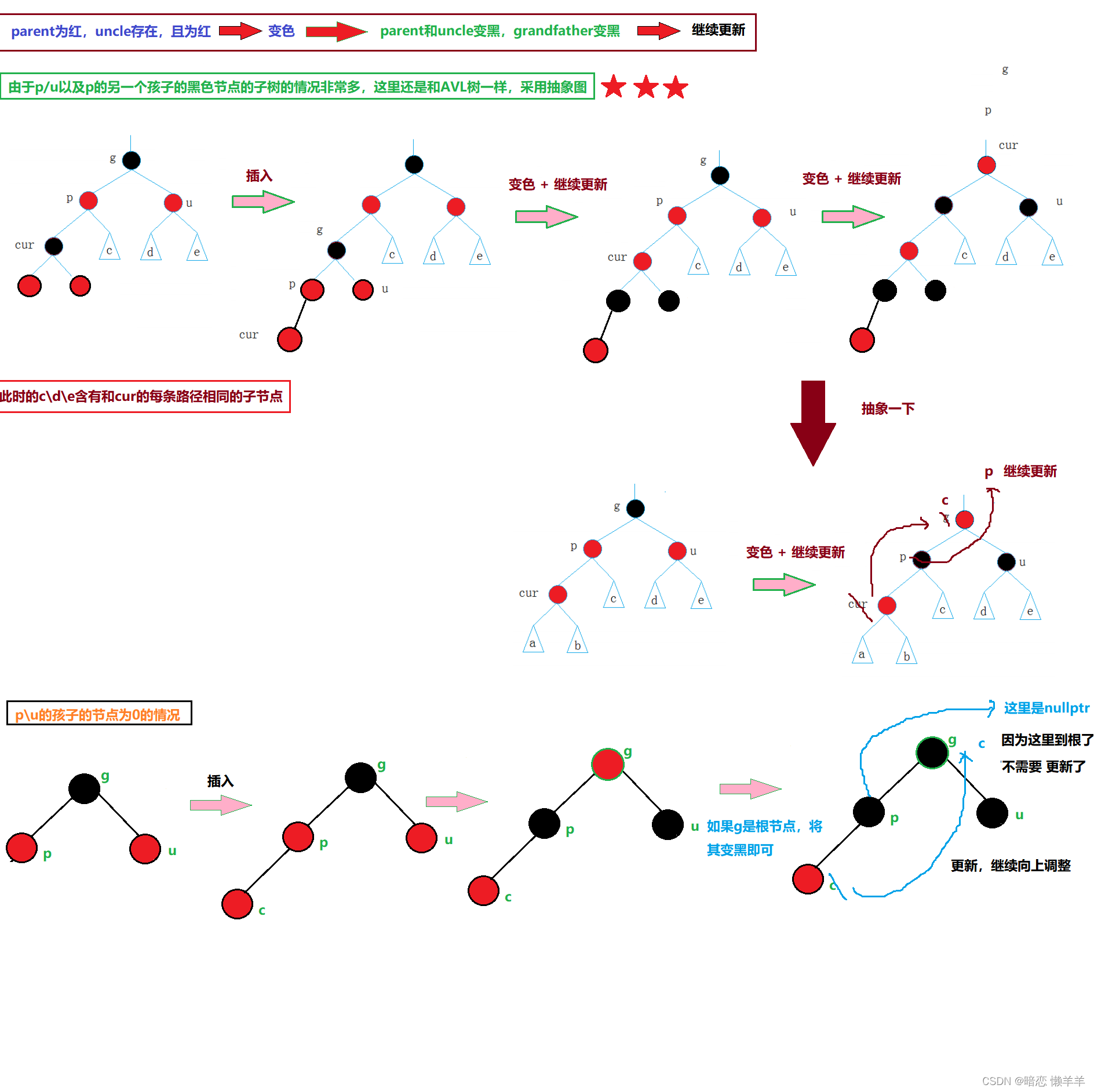
这里只画了parent在爷爷的左边的情况,如果parent在爷爷的右边和这个是一样的!
parent为红,叔叔不存在会存在为黑(变色 + 旋转)
如果parent在爷爷的左,且cur在父亲的左,对爷爷进行右单旋;
如果parent在爷爷的左,且cur在父亲的右,先对parent左单旋,在对爷爷进行右单旋;
如果parent在爷爷的右,且cur在父亲的右,对爷爷进行左单旋;
如果parent在爷爷的右,且cur在父亲的左,先对parent右单旋,在对爷爷进行左单旋;
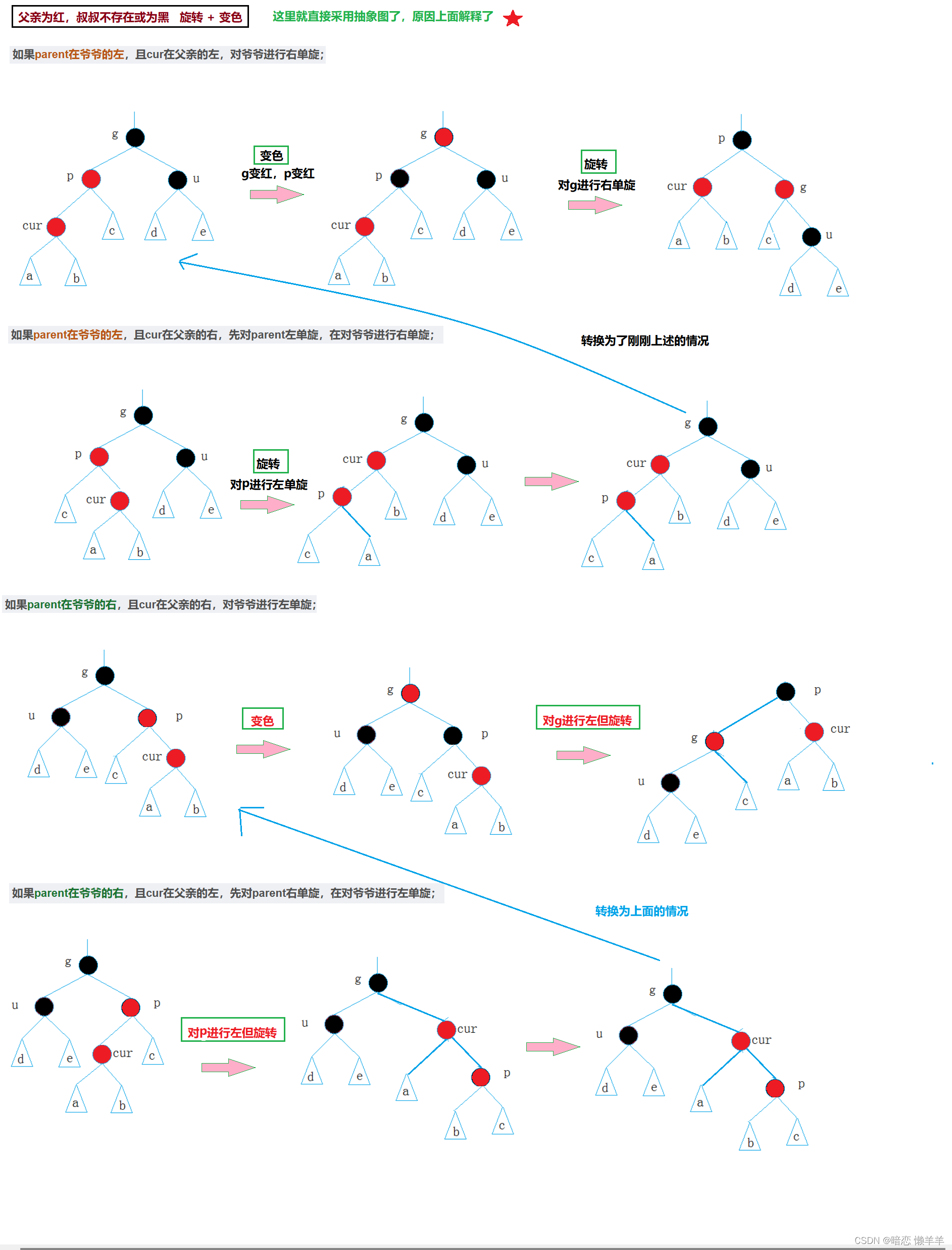
OK,废话不多说直接上代码:
bool Insert(const pair<K, V>& kv)
{Node* cur = _root;//当前节点Node* parent = nullptr;//插入位置的父亲//第一次插入if (_root == nullptr){_root = new Node(kv);_size++;//插入成功节点数+1_root->_col = BLACK;//根节点是黑色return true;}//寻找插入的位置while (cur){if (cur->_kv.first < kv.first)//插入节点的key比当前节点的key大{parent = cur;cur = cur->_right;//去右边找}else if(cur->_kv.first > kv.first)//插入节点的key比当前节点的key小{parent = cur;cur = cur->_left;//去左边找}else{return false;//插入的节点存在}}//找到插入位置cur = new Node(kv);//链接if (parent->_kv.first > cur->_kv.first){parent->_left = cur;}else{parent->_right = cur;}cur->_parent = parent;//颜色和高度调整while (parent && parent->_col == RED){Node* grandfather = parent->_parent;if (parent == grandfather->_left)//父亲在爷爷的左{Node* uncle = grandfather->_right;//叔叔就是父亲的右//父亲存在且为红 -> 变色if (uncle && uncle->_col == RED){grandfather->_col = RED;parent->_col = uncle->_col = BLACK;//继续向上调整cur = grandfather;parent = cur->_parent;}else//叔叔不存在或存在但为黑 -> 变色 + 旋转{if (cur == parent->_left)//cur在父亲的左{// g// p u// cRotateR(grandfather);//旋转parent->_col = BLACK;//变色grandfather->_col = RED;}else//cur在父亲的右{// g// p u// cRotateL(parent);//旋转RotateR(grandfather);cur->_col = BLACK;//变色grandfather->_col = RED;}break;//旋转后不需要再向上更新了}}else//parent在爷爷的右{Node* uncle = grandfather->_left;//叔叔在父亲的左//叔叔存在且为红 -> 变色if (uncle && uncle->_col == RED){grandfather->_col = RED;parent->_col = uncle->_col = BLACK;//继续向上调整cur = grandfather;parent = cur->_parent;}else//叔叔不存在或存在但为黑 -> 变色 + 旋转{if (cur == parent->_left)//cur在父亲的左 {// g// u p// cRotateR(parent);//旋转RotateL(grandfather);cur->_col = BLACK;//变色grandfather->_col = RED;}else{// g// u p// cRotateL(grandfather);//旋转parent->_col = BLACK;//变色grandfather->_col = RED;}break;//旋转后不需要再向上更新了}}}_root->_col = BLACK;//保证根节点永远是黑色_size++;//插入成功节点数+1return true;
}旋转
红黑树的旋转没有,AVL的复杂,只有左右单旋且没有平衡因子!整体的逻辑和AVL一样的,这里不在详细介绍了!
void RotateR(Node* parent)
{Node* subL = parent->_left;//父亲的左Node* subLR = subL->_right;//左子树的右Node* ppNode = parent->_parent;//parent的父节点,方便旋转后的链接parent->_left = subLR;//将左子树的右给父亲的做if (subLR)subLR->_parent = parent;subL->_right = parent;//parent做左子树的右parent->_parent = subL;if (parent == _root)//parent是根{_root = subL;//此时的新根就是subLppNode = nullptr;}else//parent不是根{//将新的根连接到ppNodeif (ppNode->_left == parent){ppNode->_left = subL;}else{ppNode->_right = subL;}subL->_parent = ppNode;}
}void RotateL(Node* parent)
{Node* subR = parent->_right;//父亲的右Node* subRL = subR->_left;//右子树的左Node* ppNode = parent->_parent;//parent的父节点,方便旋转后的链接parent->_right = subRL;//将右子树的左连接到parent的右if (subRL)subRL->_parent = parent;subR->_left = parent;//parent连接到subR的左parent->_parent = subR;if (parent == _root)//parent是根{_root = subR;//此时的新根就是subRppNode = nullptr;}else//parent不是根{//将新的根连接到ppNodeif (ppNode->_left == parent){ppNode->_left = subR;}else{ppNode->_right = subR;}subR->_parent = ppNode;}
}OK,我们验证一下,判断一下是否是平衡的:
是否平衡
先获取任意一条路径的黑色节点,然后通过dfs进行检查每个结点是不是符合红黑树的规则!
如果出现连续的红色节点,不符合!判断方式:当出现红色节点时,检查其父节点是否是红色的,如果是则不符合!
如走到空了,检查该条路径的黑色节点和一开始求出的是否一致,不一致则不符合!
当前节点符合,去检查其左右!
bool IsBalance()
{if (_root && _root->_col == RED){return false;//根为红,一定不是红黑树}int black = 0;//获取任意一条路径的黑色节点(这里是最左路)Node* cur = _root;while (cur){if (cur->_col == BLACK){black++;}cur = cur->_left;}return Check(_root, black, 0);
}bool Check(Node* root, const int black, int num)
{if (root == nullptr){//当走到叶子节点的时候和其他路径的黑色节点的个数不一样if (black != num){return false;}return true;}//存在连续的红色节点if (root->_col == RED && root->_parent && root->_parent->_col == RED){cout << root->_kv.first << " :存在连续的红色节点" << endl;return false;}//遇到黑色节点++if (root->_col == BLACK){num++;}//当前节点符合红黑树,它的左右子树也要都符合return Check(root->_left, black, num) && Check(root->_right, black, num);
}OK,验证一下:
OK,么有问题!下面把其他的接口补一下!
Size
由于我们提前记录了_size所以直接返回成员_size即可!
size_t Size()
{return _size;
}Find
和以前的搜索树一样,大了去右边找,小了去左边找!
Node* Find(const K& key)
{Node* cur = _root;while (cur){if (cur->_kv.first < key)//插入节点的key比当前节点的key大{cur = cur->_right;//去右边找}else if (cur->_kv.first > key)//插入节点的key比当前节点的key小{cur = cur->_left;//去左边找}else{return cur;//找到了}}return nullptr;//没找到
}
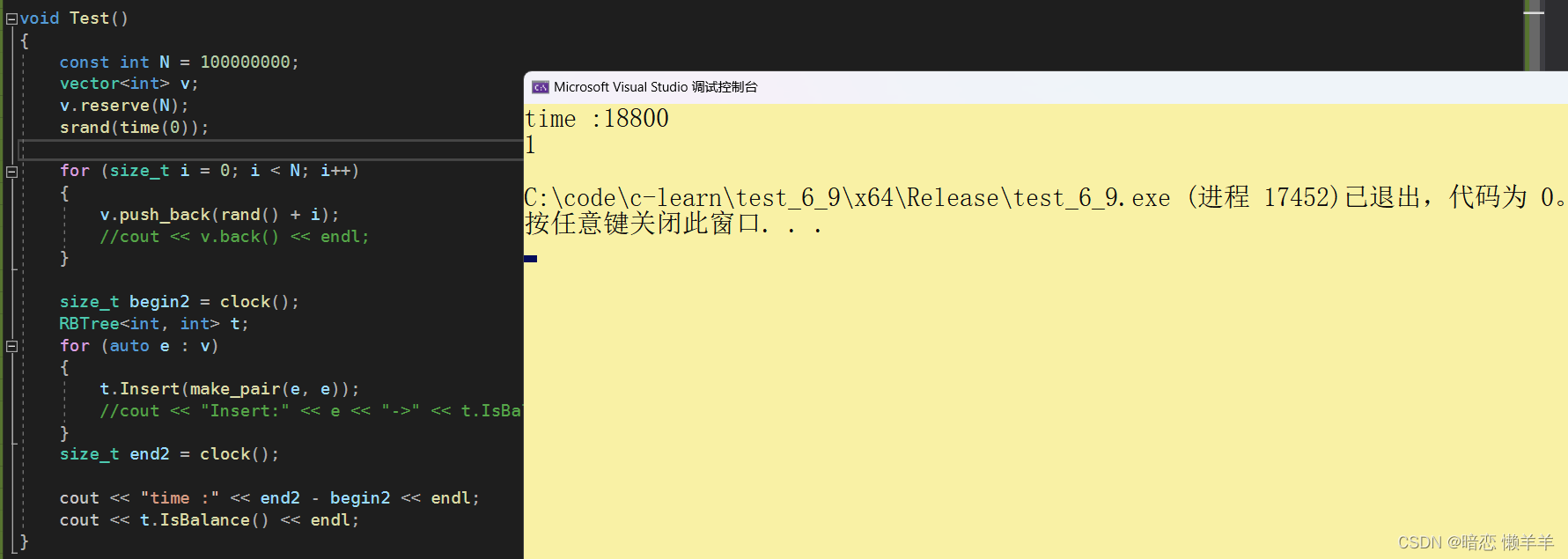
再来一组随机的测试用例:插入1亿个随机值,看看时间和是否平衡(注意这里一亿个节点在32位debug下可能内存空间不够,可以把他改成64的release地址空间大一点)
void Test()
{const int N = 100000000;vector<int> v;v.reserve(N);srand(time(0));for (size_t i = 0; i < N; i++){v.push_back(rand() + i);//cout << v.back() << endl;}size_t begin2 = clock();RBTree<int, int> t;for (auto e : v){t.Insert(make_pair(e, e));//cout << "Insert:" << e << "->" << t.IsBalance() << endl;}size_t end2 = clock();cout << "time :" << end2 - begin2 << endl;cout << t.IsBalance() << endl;
}
红黑树的删除:请参考这篇博客 :红黑树的删除
全部源码
#pragma onceenum Col//颜色
{RED,BLACK
};template<class K, class V>
struct RBTreeNode
{RBTreeNode<K, V>* _left;//左孩子RBTreeNode<K, V>* _right;//右孩子RBTreeNode<K, V>* _parent;//父结点pair<K, V> _kv;//数据域Col _col;//颜色RBTreeNode(const pair<K,V>& kv):_left(nullptr),_right(nullptr),_parent(nullptr),_kv(kv),_col(RED)//新插入的节点默认是红色{}
};template<class K, class V>
class RBTree
{typedef RBTreeNode<K, V> Node;
public:RBTree():_root(nullptr),_size(0){}bool Insert(const pair<K, V>& kv){Node* cur = _root;//当前节点Node* parent = nullptr;//插入位置的父亲//第一次插入if (_root == nullptr){_root = new Node(kv);_size++;//插入成功节点数+1_root->_col = BLACK;//根节点是黑色return true;}//寻找插入的位置while (cur){if (cur->_kv.first < kv.first)//插入节点的key比当前节点的key大{parent = cur;cur = cur->_right;//去右边找}else if(cur->_kv.first > kv.first)//插入节点的key比当前节点的key小{parent = cur;cur = cur->_left;//去左边找}else{return false;//插入的节点存在}}//找到插入位置cur = new Node(kv);//链接if (parent->_kv.first > cur->_kv.first){parent->_left = cur;}else{parent->_right = cur;}cur->_parent = parent;//颜色和高度调整while (parent && parent->_col == RED){Node* grandfather = parent->_parent;if (parent == grandfather->_left)//父亲在爷爷的左{Node* uncle = grandfather->_right;//叔叔就是父亲的右//父亲存在且为红 -> 变色if (uncle && uncle->_col == RED){grandfather->_col = RED;parent->_col = uncle->_col = BLACK;//继续向上调整cur = grandfather;parent = cur->_parent;}else//叔叔不存在或存在但为黑 -> 变色 + 旋转{if (cur == parent->_left)//cur在父亲的左{// g// p u// cRotateR(grandfather);//旋转parent->_col = BLACK;//变色grandfather->_col = RED;}else//cur在父亲的右{// g// p u// cRotateL(parent);//旋转RotateR(grandfather);cur->_col = BLACK;//变色grandfather->_col = RED;}break;//旋转后不需要再向上更新了}}else//parent在爷爷的右{Node* uncle = grandfather->_left;//叔叔在父亲的左//叔叔存在且为红 -> 变色if (uncle && uncle->_col == RED){grandfather->_col = RED;parent->_col = uncle->_col = BLACK;//继续向上调整cur = grandfather;parent = cur->_parent;}else//叔叔不存在或存在但为黑 -> 变色 + 旋转{if (cur == parent->_left)//cur在父亲的左 {// g// u p// cRotateR(parent);//旋转RotateL(grandfather);cur->_col = BLACK;//变色grandfather->_col = RED;}else{// g// u p// cRotateL(grandfather);//旋转parent->_col = BLACK;//变色grandfather->_col = RED;}break;//旋转后不需要再向上更新了}}}_root->_col = BLACK;//保证根节点永远是黑色_size++;//插入成功节点数+1return true;}Node* Find(const K& key){Node* cur = _root;while (cur){if (cur->_kv.first < key)//插入节点的key比当前节点的key大{cur = cur->_right;//去右边找}else if (cur->_kv.first > key)//插入节点的key比当前节点的key小{cur = cur->_left;//去左边找}else{return cur;//找到了}}return nullptr;//没找到}void InOrder(){return _InOrder(_root);}size_t Size(){return _size;}bool IsBalance(){if (_root && _root->_col == RED){return false;//根为红,一定不是红黑树}int black = 0;//获取任意一条路径的黑色节点(这里是最左路)Node* cur = _root;while (cur){if (cur->_col == BLACK){black++;}cur = cur->_left;}return Check(_root, black, 0);}private:void _InOrder(Node* root){if (root == nullptr)return;_InOrder(root->_left);cout << root->_kv.first << ":" << root->_kv.second << endl;_InOrder(root->_right);}void RotateR(Node* parent){Node* subL = parent->_left;//父亲的左Node* subLR = subL->_right;//左子树的右Node* ppNode = parent->_parent;//parent的父节点,方便旋转后的链接parent->_left = subLR;//将左子树的右给父亲的做if (subLR)subLR->_parent = parent;subL->_right = parent;//parent做左子树的右parent->_parent = subL;if (parent == _root)//parent是根{_root = subL;//此时的新根就是subLppNode = nullptr;}else//parent不是根{//将新的根连接到ppNodeif (ppNode->_left == parent){ppNode->_left = subL;}else{ppNode->_right = subL;}subL->_parent = ppNode;}}void RotateL(Node* parent){Node* subR = parent->_right;//父亲的右Node* subRL = subR->_left;//右子树的左Node* ppNode = parent->_parent;//parent的父节点,方便旋转后的链接parent->_right = subRL;//将右子树的左连接到parent的右if (subRL)subRL->_parent = parent;subR->_left = parent;//parent连接到subR的左parent->_parent = subR;if (parent == _root)//parent是根{_root = subR;//此时的新根就是subRppNode = nullptr;}else//parent不是根{//将新的根连接到ppNodeif (ppNode->_left == parent){ppNode->_left = subR;}else{ppNode->_right = subR;}subR->_parent = ppNode;}}bool Check(Node* root, const int black, int num){if (root == nullptr){//当走到叶子节点的时候和其他路径的黑色节点的个数不一样if (black != num){return false;}return true;}//存在连续的红色节点if (root->_col == RED && root->_parent && root->_parent->_col == RED){cout << root->_kv.first << " :存在连续的红色节点" << endl;return false;}//遇到黑色节点++if (root->_col == BLACK){num++;}//当前节点符合红黑树,它的左右子树也要都符合return Check(root->_left, black, num) && Check(root->_right, black, num);}private:Node* _root;//根节点size_t _size;//节点的数量
};
红黑树的效率分析以及应用
红黑树和AVL树的比较
红黑树和AVL树都是高效的平衡二叉树,增删改查的时间复杂度都是O(log_2 N),红黑树不追 求绝对平衡,其只需保证最长路径不超过最短路径的2倍,相对而言,降低了插入和旋转的次数, 所以在经常进行增删的结构中性能比AVL树更优,而且红黑树实现比较简单,所以实际运用中红黑树更多。
红黑树的应用
C++的STL库中的map/set/multimap/multiset底层都是红黑树实现的
一些Java的库;例如: TreeMap和TreeSet等
一些Linux的内核,例如:进程调度等
OK,本期分享就到这里,好兄弟,我们下期再见!
结束语:简单的事重复做,重复的是坚持做!
相关文章:

红黑树的介绍与实现
前言 前面我们介绍了AVL树,AVL树是一棵非常自律的树,有着严格的高度可控制!但是正它的自律给他带来了另一个问题,即虽然他的查找效率很高,但是插入和删除由于旋转而导致效率没有那么高。我们上一期的结尾说过经常修改…...

easyexcel将csv转为excel处理数字问题
使用easyexcel可以将csv格式的文件转为.xlsx文件,但是csv中有很多数字,比如:"123","12.34","-111",默认情况下会将其作为字符串写入.xlsx文件,就如同下面一样,字符类型的数字…...

DDMA信号处理以及数据处理的流程---随机目标生成
Hello,大家好,我是Xiaojie,好久不见,欢迎大家能够和Xiaojie一起学习毫米波雷达知识,Xiaojie准备连载一个系列的文章—DDMA信号处理以及数据处理的流程,本系列文章将从目标生成、信号仿真、测距、测速、cfar…...

爬虫实现思路
现在的人工智能太强大了,只要有问题,输入后就能给出大致的实现思路;我看了下确实没问题,只需要更改一些细节基本就能拿来就用;下面是我实验经历: 问题: c# 书写爬虫爬取按动物名称,…...
神经网络 torch.nn---Non-Linear Activations (ReLU)
ReLU — PyTorch 2.3 documentation torch.nn - PyTorch中文文档 (pytorch-cn.readthedocs.io) 非线性变换的目的 非线性变换的目的是为神经网络引入一些非线性特征,使其训练出一些符合各种曲线或各种特征的模型。 换句话来说,如果模型都是直线特征的…...
【微服务】使用kubekey部署k8s多节点及kubesphere
kubesphere官方部署文档 https://github.com/kubesphere/kubesphere/blob/master/README_zh.md kubuctl命令文档 https://kubernetes.io/zh-cn/docs/reference/kubectl/ k8s资源类型 https://kubernetes.io/zh-cn/docs/reference/kubectl/#%E8%B5%84%E6%BA%90%E7%B1%BB%E5%9E…...

目标检测数据集 - 垃圾桶满溢检测数据集下载「包含VOC、COCO、YOLO三种格式」
数据集介绍:垃圾桶满溢检测数据集,真实场景高质量图片数据,涉及场景丰富,比如城市道边垃圾桶满溢、小区垃圾桶满溢、社区垃圾桶满溢、农村道边垃圾桶满溢、垃圾集中处理点垃圾桶满溢、公园垃圾桶满溢数据等。数据集标注标签划分为…...
)
6.9总结(省赛排位赛1)
省赛排位赛1省赛排名赛1 - Virtual Judge (vjudge.net) 思路: 其实就是一个斐波拉契数列,当前项前两项之和,先将范围内的数全部存起来放进一个数组,再进行累加查询 代码: #define _CRT_SECURE_NO_WARNINGS 1 #incl…...

58.CountdownLatch
用来进行线程同步协作,等待所有线程完成倒计时。 构造参数用来初始化等待计数值,await方法用来等待计数归零,countDown方法用来让计数减一。 CountdownLatch普通使用 @Slf4j public class CountdownLatchDemo {public static void main(String[] args) {CountDownLatch c…...

Java数据结构准备工作---常用类
文章目录 前言1.包装类1.1.包装类基本知识1.2.包装类的用途1.3.装箱和拆箱1.3.1.装箱:1.3.2.拆箱 1.4 包装类的缓存问题 2.时间处理类2.1.Date 时间类(java.util.Date)2.2.DateFormat 类和 SimpleDateFormat 类2.3.Calendar 日历类 3.其他常用类3.1.Math类3.2.Rando…...

SD 使用教程
SD 换脸步骤 使用Stable Diffusion (SD) 进行换脸的基本步骤可以从以下几个方面概述,这里以一种常见的方式为例,结合了插件的使用来简化流程: 准备工作 安装必要的软件和插件:首先,确保你已经安装了Stable Diffusion…...

Sylar---协程调度模块
协程调度模块: 首先是协程任务类FiberAndThread,包括协程,函数,指定的线程;提供了五个构造函数,只传协程的智能指针,只传函数对象,传协程智能指针的指针,函数对象指针,还…...

iOS Hook 崩溃
0x00 崩溃重现 被 Hook 的类,是这样的: interface ViewController : UIViewController endimplementation ViewController - (void)loadView {[super loadView];NSLog("%s", __func__); }- (void)test {NSLog("%s", __func__); }-…...

区间预测 | Matlab实现LSTM-ABKDE长短期记忆神经网络自适应带宽核密度估计多变量回归区间预测
区间预测 | Matlab实现LSTM-ABKDE长短期记忆神经网络自适应带宽核密度估计多变量回归区间预测 目录 区间预测 | Matlab实现LSTM-ABKDE长短期记忆神经网络自适应带宽核密度估计多变量回归区间预测效果一览基本介绍程序设计参考资料 效果一览 基本介绍 1.Matlab实现LSTM-ABKDE长…...
相关笔记汇总)
linux内核下rapidio(TSI721)相关笔记汇总
1 驱动的安装 和 主要功能(doorbell, DMA, rionet)的简单测试 linux5.4 下使用rapidio(tsi721)的笔记记录_kernel-rapidio-CSDN博客 2 机理分析 linux内核下,rapidio网络系统建立的过程(枚举 和 发现)_linux rapidio-CSDN博客 linux内核下,(rapidio)T…...

从GPT-4到GPT-4o:人工智能的进化与革命
从GPT-4到GPT-4o:人工智能的进化与革命 近期,OpenAI推出了最新版本的人工智能模型——GPT-4o,引发了广泛的关注和讨论。在这篇文章中,我们将对GPT-4o进行全面评价,包括与前一版本GPT-4的对比分析,GPT-4o的…...

【Java】/*抽象类和接口*/
目录 一、抽象类和抽象方法 1.1 概念 1.2 特性 1.3 作用 二、接口 2.1 概念及定义 2.2 特性 2.3 实例:笔记本电脑 2.4 一个类可以实现多个接口 2.5 一个接口可以继承多个接口 2.6 Comparable接口 2.7 Comparator接口 2.8 Cloneable接口 2.9 浅拷贝和深…...
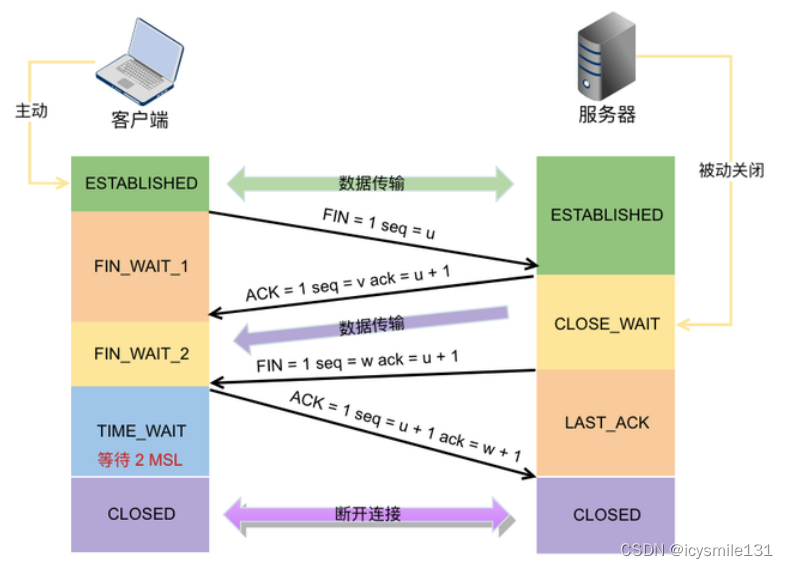
TCP/IP协议介绍——三次握手四次挥手
TCP/IP(Transmission Control Protocol/Internet Protocol,传输控制协议/网际协议)是指能够在多个不同网络间实现信息传输的协议簇。TCP/IP协议不仅仅指的是TCP 和IP两个协议,而是指一个由FTP、SMTP、TCP、UDP、IP等协议构成的协议…...
[C++]基于C++opencv结合vibe和sort tracker实现高空抛物实时检测
【vibe算法介绍】 ViBe算法是一种高效的像素级视频背景建模和前景检测算法。以下是对该算法的详细介绍: 一、算法原理 ViBe算法的核心思想是通过为每个像素点存储一个样本集,利用该样本集与当前像素值进行比较,从而判断该像素是否属于背景…...
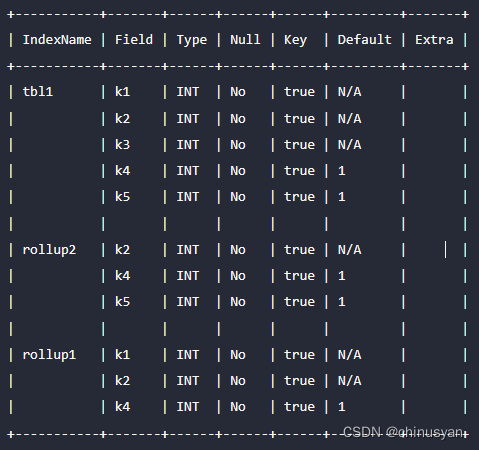
Apache Doris 基础 -- 数据表设计(模式更改)
用户可以通过schema Change操作修改现有表的模式。表的模式主要包括对列的修改和对索引的修改。这里我们主要介绍与列相关的Scheme更改。对于与索引相关的更改,可以查看数据表设计/表索引,查看每个索引的更改方法。 1、术语 基本表(Base Ta…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...
