【TensorFlow深度学习】值函数估计:蒙特卡洛方法与TD学习
值函数估计:蒙特卡洛方法与TD学习
- 值函数估计:蒙特卡洛方法与TD学习的深度探索
- 蒙特卡洛方法
- 时序差分学习(TD)
- Python代码示例
- 结论
值函数估计:蒙特卡洛方法与TD学习的深度探索
在强化学习的奇妙世界里,值函数估计扮演着至关重要的角色,它使智能体能够评估在特定状态下或执行特定动作后的长期收益。在这一框架下,蒙特卡洛方法和时序差分(TD)学习是两种核心策略,用于近似未来奖励的累计值。本文将深入解析这两种方法的原理,并通过Python代码示例,带你亲历它们在实践中的应用与差异。
蒙特卡洛方法
蒙特卡洛(Monte Carlo, MC)方法是一种基于采样的策略,它通过完整地运行多个试验(episode),直到结束,然后平均这些试验的回报来估计状态或状态-动作的价值。这种方法不需要模型,适用于 episodic 任务,并且在长期奖励占主导时特别有效。
时序差分学习(TD)
时序差分(Temporal Difference, TD)学习则是一种在线学习方法,它通过比较当前状态和下一个状态的预测值来更新估计值函数,即“时序差分”。TD方法可以在每个时间步进行更新,不必等待episode结束,因此能更快地收敛,尤其是在延迟奖励任务中。
Python代码示例
假设有一个简单的老虎机游戏环境,我们用MC和TD(0)方法估计状态值函数。
环境定义
class BanditEnv:def __init__(self, probabilities=[0.2, 0.5, 0.7]):self.probabilities = probabilitiesself.n_arms = len(probabilities)def step(self, action):if np.random.rand() < self.probabilities[action]:return 1 # Winelse:return 0 # Lose
蒙特卡洛方法示例
def mc_prediction(env, num_episodes, alpha=0.1):returns_sum = np.zeros(env.n_arms)n_a = np.zeros(env.n_arms)values = np.zeros(env.n_arms)for episode in range(num_episodes):chosen_arm = np.random.randint(env.n_arms) # 选择一个臂reward = 0for _ in range(100): # 假设episode长度为100步reward += env.step(chosen_arm)returns_sum[chosen_arm] += rewardn_a[chosen_arm] += 1values = returns_sum / n_areturn values
TD(0)学习示例
def td_prediction(env, num_episodes, alpha=0.1, gamma=0.9):values = np.zeros(env.n_arms)for episode in range(num_episodes):chosen_arm = np.random.randint(env.n_arms)reward = env.step(chosen_arm)values[chosen_arm] += alpha * (reward + gamma * values[chosen_arm] - values[chosen_arm])return values
结论
通过上述代码示例,我们可以直观感受到蒙特卡洛方法和TD学习的不同之处。蒙特卡洛方法需要等到episode结束后才更新,每一次更新基于整个episode的回报,因此更新频率低,但更直接反映实际收益;而TD学习则在每个步骤更新,利用即时反馈和当前估计的未来价值,更新更频繁,能更快地逼近真实值,尤其在长序列决策中优势明显。
在实际应用中,选择哪种方法取决于任务特性:对于episodic且较短的任务,蒙特卡洛可能更直接有效;而对于连续决策,需要快速反馈的场景,TD学习更合适。当然,现代强化学习中,往往结合二者优势,如TD(λ)算法,融合了MC的全局更新和TD的即时更新,以达到更优的性能。探索这些方法的边界与融合,正是强化学习魅力所在。
相关文章:

【TensorFlow深度学习】值函数估计:蒙特卡洛方法与TD学习
值函数估计:蒙特卡洛方法与TD学习 值函数估计:蒙特卡洛方法与TD学习的深度探索蒙特卡洛方法时序差分学习(TD)Python代码示例结论 值函数估计:蒙特卡洛方法与TD学习的深度探索 在强化学习的奇妙世界里,值函数估计扮演着至关重要的…...

成功解决ModuleNotFoundError: No module named ‘cv2’
成功解决ModuleNotFoundError: No module named ‘cv2’ 🌈 欢迎莅临我的个人主页👈这里是我深耕Python编程、机器学习和自然语言处理(NLP)领域,并乐于分享知识与经验的小天地!🎇 🎓…...

中国蚁剑 安装教程 2024年5月
2024/5/11 中国蚁剑 安装教程 一、下载中国蚁剑的加载器和核心源码(两个都要用到) github官方下载地址:https://github.com/AntSwordProject/ 参考文档:antSword/README_CN.md at master AntSwordProject/antSword GitHub 核…...
Golang-分离式加载器(传参)AES加密
目录 enc.go 生成: dec.go --执行dec.go...--上线 cs生成个c语言的shellcode. enc.go go run .\enc.go shellcode 生成: --key为公钥. --code为AES加密后的数据, ----此脚本每次运行key和code都会变化. package mainimport ("bytes""crypto/aes"&…...

速览三版HTTP的改进策略
HTTP(Hypertext Transfer Protocol)是互联网通信的基础协议,自从其第一个版本推出以来,经历了多个版本的改进,每个版本都针对之前的不足进行了优化和增强。以下是HTTP/1.1、HTTP/2和HTTP/3的主要改进总结: …...
 执行是下载,并没有打开新窗口显示html)
window.open(“.html“,“_blank“) 执行是下载,并没有打开新窗口显示html
window.open() 方法在浏览器中打开一个新窗口或者新标签页。如果你的 .html 文件被下载而不是在新窗口中打开,那可能是因为服务器的响应头设置了 Content-Disposition: attachment,这会导致浏览器把响应的内容作为一个文件下载。 如果你有权限修改服务器…...
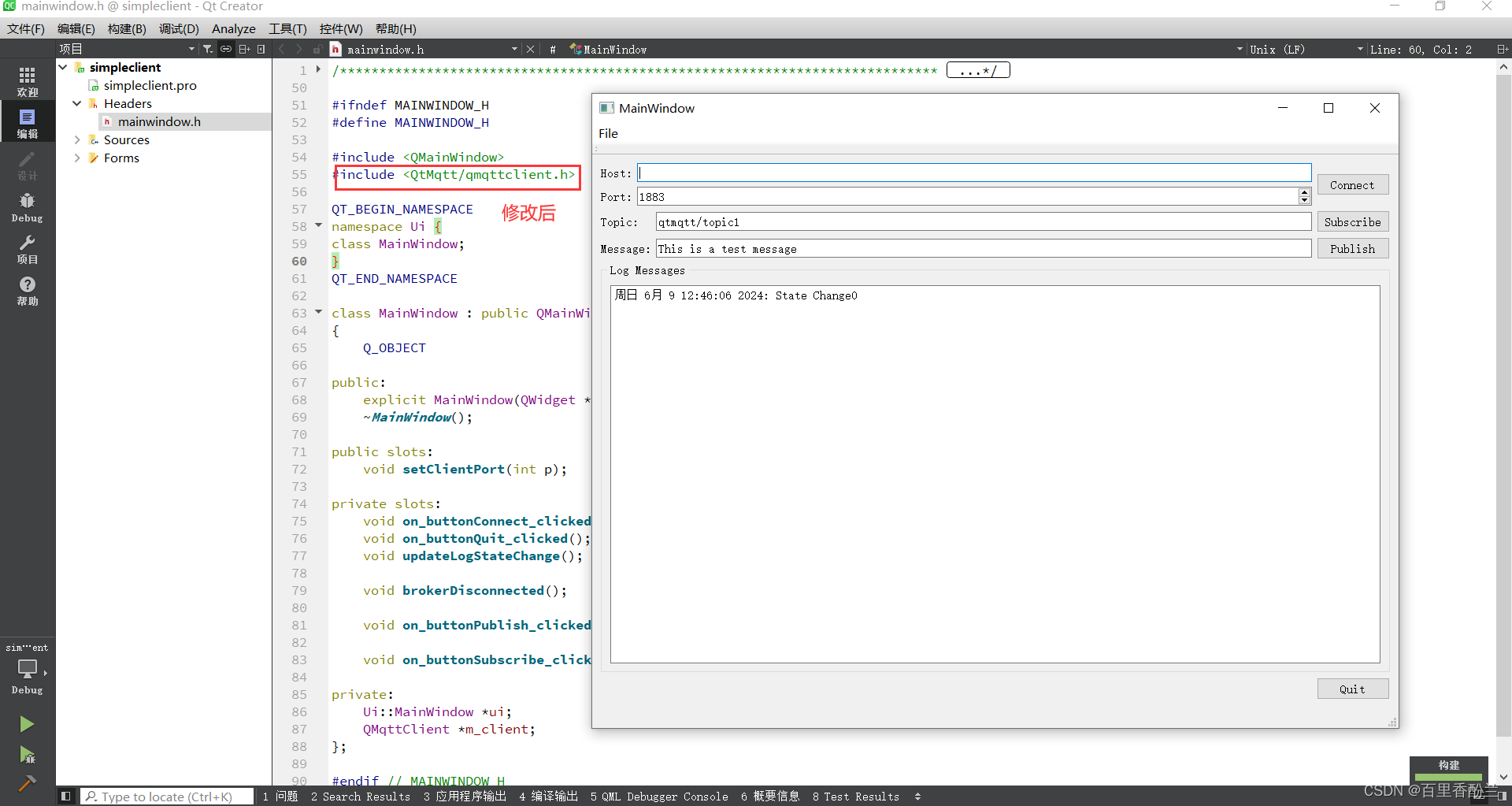
【QT5.14.2】编译MQTT库example的时候报No such file or directory
【QT5.14.2】编译MQTT库example的时候报No such file or directory 前几天导师让跑一下MQTT库,用的5.14.2版本的QT,于是就上网搜了一个教程:https://www.bilibili.com/video/BV1dH4y1e7hG/?spm_id_from333.337.search-card.all.click&v…...

【数据结构】前缀树(字典树)汇总
基础 {“a”,“abc”,“bac”,“bbc”,“ca” }的字典树如下图: 最主用的应用:一,字符串编码。二,位运算。 字符串编码 相比利用哈希映射编码,优点如下: 依次查询长度为n的字符串s的前缀时间复杂度是O(…...
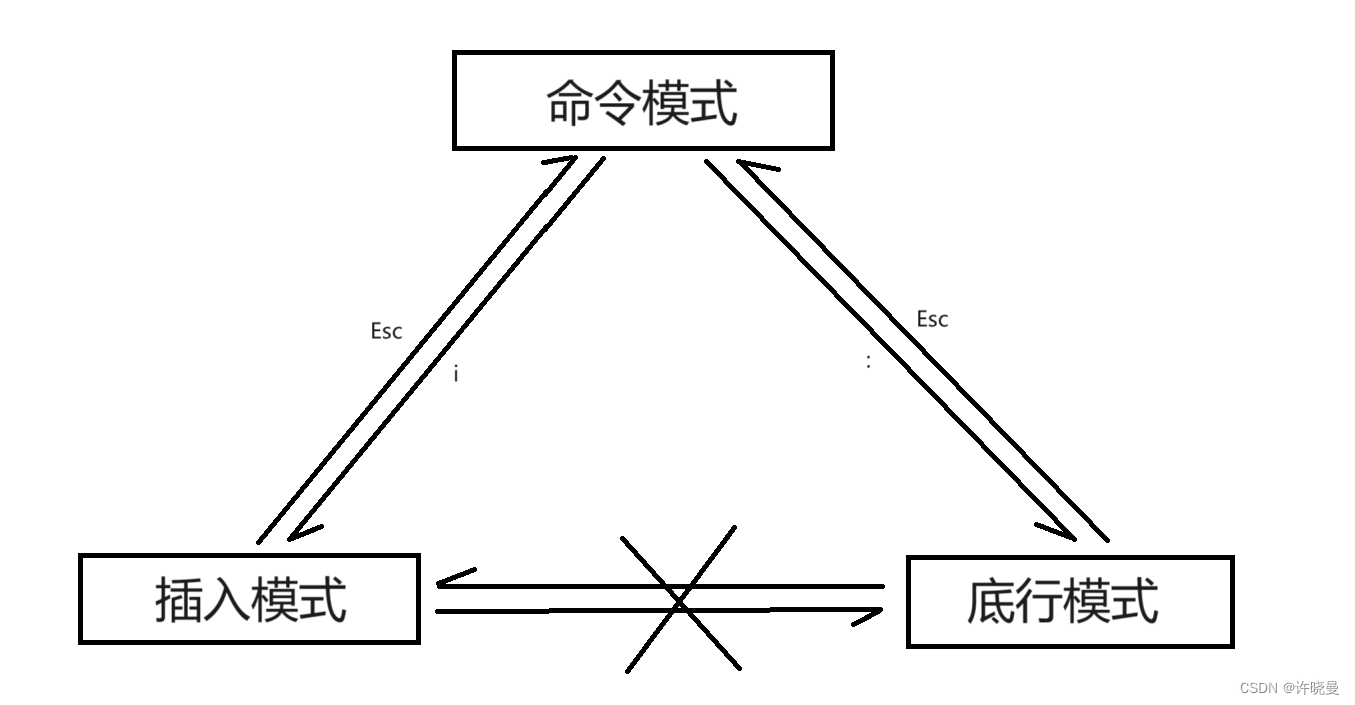
Linux:基础开发工具
文章目录 Linux 软件包管理器 yum什么是软件包关于rzsz查看软件包安装软件卸载软件安装扩展源 Linux 编辑器 vimvim的基本概念正常/普通/命令模式(Normal mode)插入模式(Insert mode)底行模式(last line mode) vim的基本操作[命令模式]切换至[插入模式][插入模式]切换至[命令模…...

HarmonyOS NEXT Push接入
接入HarmonyOS NEXT Push 推送功能,相比于 Android 真的是简单太多。不再需要适配接入各个厂家的推送 SDK,真是舒服。 1.开通推送服务与配置Client ID 1.1 创建应用获取Client ID 按照官方文档来就可以了:https://developer.huawei.com/co…...

如何快速入门Element-UI:打造高效美观的前端界面
Element-UI 是一款基于 Vue.js 的开源组件库,提供了丰富的 UI 组件,可以帮助开发者快速构建美观、响应式的前端界面。本文将详细介绍如何快速入门 Element-UI,包括环境搭建、组件使用、样式定制及常见问题解决方法,帮助你高效地使用 Element-UI 进行前端开发。 一、环境搭…...

Langchain的向量存储 - Document示例代码里的疑问
文章目录 前言一、语句分析二、 举例解释三、 完整代码总结 前言 之前的代码里有下面这句话,可能有看不明白的读者。 vectors [embeddings.embed(doc.page_content) for doc in docs]今天一起来看下这句话。 一、语句分析 这句话实际上是一个列表推导式&#x…...

Docker 教程-介绍-2
快速了解docker有什么。 Docker简介 Docker 是一个开源的应用容器引擎,基于Go语言开发,并遵循Apache 2.0协议。它允许开发者将应用及其依赖包打包进一个可移植的容器中,这些容器可以发布到任何支持Docker的Linux或Windows机器上,…...
 - 三语言AC题解(Python/Java/Cpp))
【2024最新华为OD-C/D卷试题汇总】[支持在线评测] 伐木工(200分) - 三语言AC题解(Python/Java/Cpp)
🍭 大家好这里是清隆学长 ,一枚热爱算法的程序员 ✨ 本系列打算持续跟新华为OD-C/D卷的三语言AC题解 💻 ACM银牌🥈| 多次AK大厂笔试 | 编程一对一辅导 👏 感谢大家的订阅➕ 和 喜欢💗 📎在线评测链接 伐木工(200分) 🌍 评测功能需要订阅专栏后私信联系清隆解…...

UltraScale+系列模块化仪器,可以同时用作控制器、算法加速器和高速数字信号处理器
基于 XCZU7EG / XCZU4EG / XCZU2EG • 灵活的模块组合 • 易于嵌入的紧凑型外观结构 • 高性能的 ARM Cortex 处理器 • 成熟的 FPGA 可编程逻辑 ,基于 IP 核的软件库 基于 Xilinx Zynq UltraScaleMPSoC 的 FPGA 技术,采用 Xilinx Zynq UltraScale&a…...
相比有哪些优势?)
Python与其他编程语言(如Java、C++)相比有哪些优势?
一、技术难点 在探讨Python与其他编程语言相比的优势时,技术难点在于如何全面、准确地把握并阐述这些优势。这需要对Python、Java、C等编程语言有深入的理解,包括它们的语法特性、应用领域、性能特点、开发效率等。 首先,Python的语法简洁明…...

Edge浏览器双击关闭标签页,双击关闭浏览器选项卡
设置》外观》自定义浏览器,开启“使用双击关闭浏览器选项卡” 设置里面搜索“双击”,这是最快的方式 鼠标滚轮单击 或者进入“设置”-“辅助功能” 呼吁已久的功能来了!Edge浏览器双击关闭标签页功能上线新 国产浏览器大多都有双击关闭标签页…...

C++ 贪心算法——跳跃游戏、划分字母区间
一:跳跃游戏 55. 跳跃游戏 题目描述:给你一个非负整数数组 nums ,你最初位于数组的 第一个下标 。数组中的每个元素代表你在该位置可以跳跃的最大长度。判断你是否能够到达最后一个下标,如果可以,返回 true ࿱…...

汽车数据应用构想(三)
上期说的,用数据去拟合停车信息的应用,那么类似的POI信息相关的场景其实都可以实现。今天讲讲用户使用频率也很高的加油/充电场景。 实际应用中,在加油场景中用户关心的通常还是价格。无论是导航还是各种加油APP/小程序,都已经很…...

体素技术在AI绘画中的革新作用
随着人工智能技术的不断进步,AI绘画已经成为艺术创作和视觉设计领域的一大趋势。在众多推动AI绘画发展的技术中,体素技术以其独特的优势,正在逐渐改变着我们对计算机生成图像的认识。本文旨在探讨体素技术在AI绘画中的应用与影响,…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...

数学建模-滑翔伞伞翼面积的设计,运动状态计算和优化 !
我们考虑滑翔伞的伞翼面积设计问题以及运动状态描述。滑翔伞的性能主要取决于伞翼面积、气动特性以及飞行员的重量。我们的目标是建立数学模型来描述滑翔伞的运动状态,并优化伞翼面积的设计。 一、问题分析 滑翔伞在飞行过程中受到重力、升力和阻力的作用。升力和阻力与伞翼面…...

Python竞赛环境搭建全攻略
Python环境搭建竞赛技术文章大纲 竞赛背景与意义 竞赛的目的与价值Python在竞赛中的应用场景环境搭建对竞赛效率的影响 竞赛环境需求分析 常见竞赛类型(算法、数据分析、机器学习等)不同竞赛对Python版本及库的要求硬件与操作系统的兼容性问题 Pyth…...

第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10+pip3.10)
第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10pip3.10) 一:前言二:安装编译依赖二:安装Python3.10三:安装PIP3.10四:安装Paddlepaddle基础框架4.1…...

Visual Studio Code 扩展
Visual Studio Code 扩展 change-case 大小写转换EmmyLua for VSCode 调试插件Bookmarks 书签 change-case 大小写转换 https://marketplace.visualstudio.com/items?itemNamewmaurer.change-case 选中单词后,命令 changeCase.commands 可预览转换效果 EmmyLua…...
之(六) ——通用对象池总结(核心))
怎么开发一个网络协议模块(C语言框架)之(六) ——通用对象池总结(核心)
+---------------------------+ | operEntryTbl[] | ← 操作对象池 (对象数组) +---------------------------+ | 0 | 1 | 2 | ... | N-1 | +---------------------------+↓ 初始化时全部加入 +------------------------+ +-------------------------+ | …...

【实施指南】Android客户端HTTPS双向认证实施指南
🔐 一、所需准备材料 证书文件(6类核心文件) 类型 格式 作用 Android端要求 CA根证书 .crt/.pem 验证服务器/客户端证书合法性 需预置到Android信任库 服务器证书 .crt 服务器身份证明 客户端需持有以验证服务器 客户端证书 .crt 客户端身份…...
