当前位置： 首页 > news >正文

CUDA 编程(1):使用Grid 和 Block分配线程

news 2026/2/10 0:17:01

1 介绍

1.1 Grid 和 Block 概念

核函数以线程为单位进行计算的函数，cuda编程会涉及到大量的线程(thread),几千个到几万个thread同时并行计算，所有的thread其实都是在执行同一个核函数。
在这里插入图片描述

  • 对于核函数(Kernel),一个核函数一般会分配1个Grid, 1个Grid又有很多个Block，1个Block中又有很多个thread，可以认为Grid和Block都是大量的thread组合：Grid > Block > thread。之所以这么划分，比如将Grid划分为多维的Block，Block划分为多维thread，它其实是为了帮助你快速索引对应的thread。
  • Grid 和Block是逻辑上意义的概念，它并不是在你的GPU硬件上实际存在的。

在这里插入图片描述
从上图可以看出，Block中有很多个thread,每个thread它都有自己的Registers和Local Memory。同时每一个Block中的thread，他们都是共享一个Shared Memory。同时一个Grid中的多个Bl

相关文章：

CUDA 编程(1):使用Grid 和 Block分配线程

1 介绍 1.1 Grid 和 Block 概念 核函数以线程为单位进行计算的函数，cuda编程会涉及到大量的线程(thread),几千个到几万个thread同时并行计算，所有的thread其实都是在执行同一个核函数。 对于核函数(Kernel),一个核函数一般会分配1个Grid, 1个Grid又有很多个Block，1个Bloc…...

编程日记 2024/6/10 11:59:48

ArcGIS for js 4.x FeatureLayer 加载、点选、高亮

安装arcgis for js 4.x 依赖&#xff1a; npm install arcgis/core 一、FeatureLayer 加载 代码如下&#xff1a; <template><view id"mapView"></view></template><script setup>import "arcgis/core/assets/esri/themes/li…...

编程日记 2024/6/10 11:57:46

倩女幽魂手游攻略：云手机自动搬砖辅助教程！

《倩女幽魂》手游自问世以来一直备受玩家喜爱&#xff0c;其精美画面和丰富的游戏内容让人沉迷其中。而如今&#xff0c;借助VMOS云手机&#xff0c;玩家可以更轻松地进行搬砖&#xff0c;提升游戏体验。 一、准备工作 下载VMOS云手机&#xff1a; 在PC端或移动端下载并安装VM…...

编程日记 2024/6/10 11:56:45

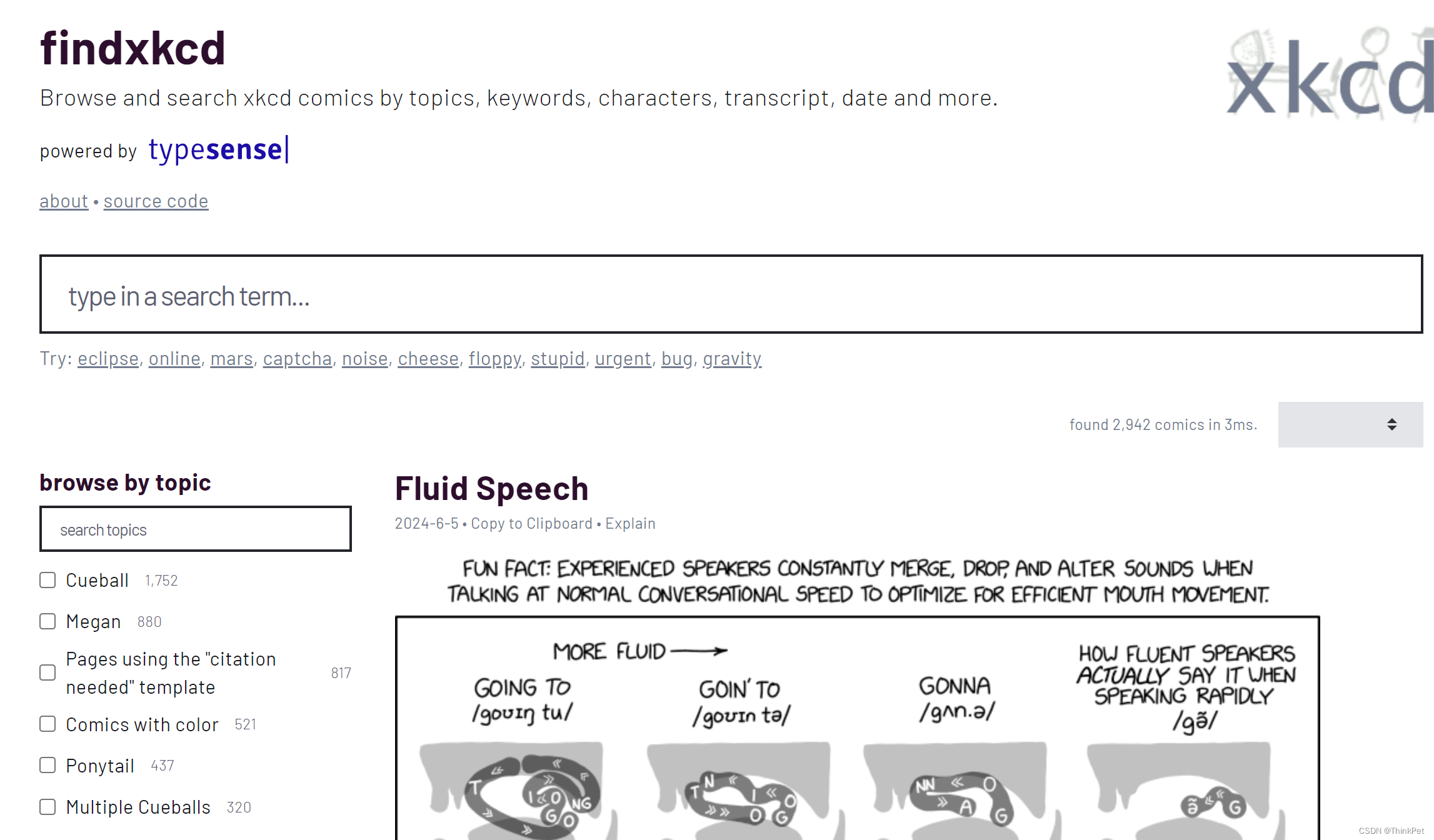
Typesense-开源的轻量级搜索引擎

Typesense-开源的轻量级搜索引擎 Typesense是一个快速、允许输入错误的搜索引擎&#xff0c;用于构建愉快的搜索体验。 开源的Algolia替代方案& 易于使用的弹性搜索替代方案 官网: https://typesense.org/ github: https://github.com/typesense/typesense 目前已有18.4k…...

编程日记 2024/6/10 11:54:43

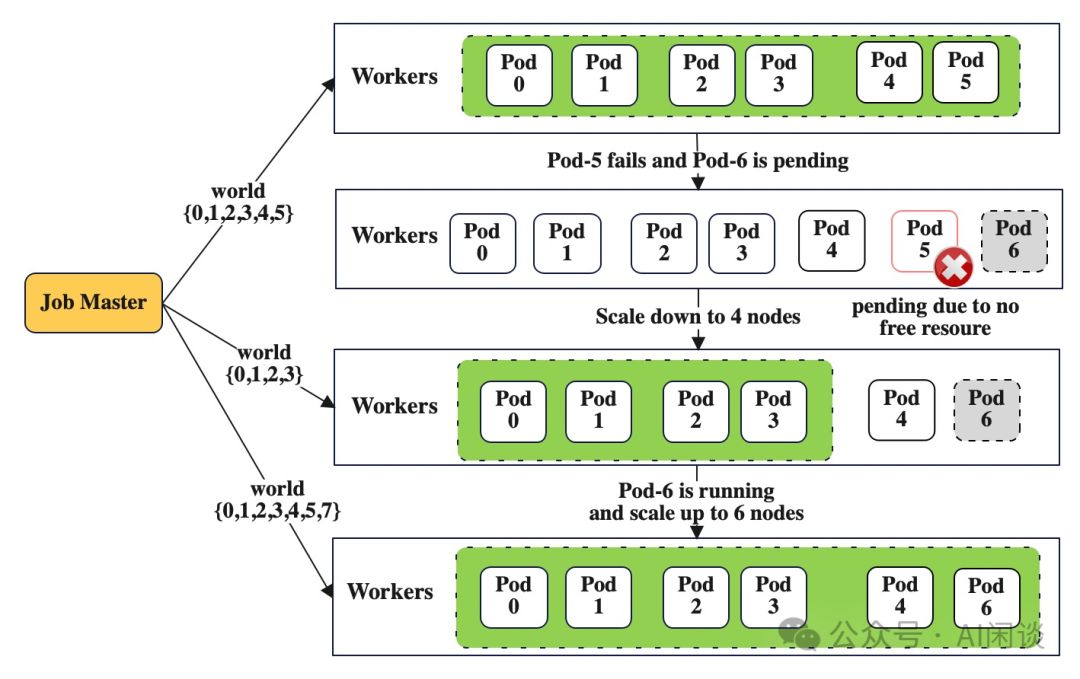
探索 LLM 预训练的挑战，GPU 集群架构实战

万卡 GPU 集群实战&#xff1a;探索 LLM 预训练的挑战 一、背景 在过往的文章中&#xff0c;我们详细阐述了LLM预训练的数据集、清洗流程、索引格式&#xff0c;以及微调、推理和RAG技术&#xff0c;并介绍了GPU及万卡集群的构建。然而&#xff0c;LLM预训练的具体细节尚待进一…...

编程日记 2024/6/10 11:53:42

高考分数查询结果自动推送至微信（卷II）

祝各位端午节安康&#xff01;只要心中无结&#xff0c;每天都是节&#xff0c;开心最重要&#xff01; 在上一篇文章高考分数查询结果自动推送至微信&#xff08;卷Ⅰ&#xff09;-CSDN博客中谈了思路&#xff0c;今天具体实现。文中将敏感信息已做处理&#xff0c;读者根据自…...

编程日记 2024/6/10 11:49:39

python类动态属性，以属性方式访问字典

动态属性能够用来描述变化的类&#xff0c;在实际应用中容易遇到用到。 import logging class Sample:def __init__(self):self.timeNoneself.sampleidNoneself.massNoneself.beizhu""self.num0self.items{}#字典属性def __getattribute__(self, attr): #注意&#…...

编程日记 2024/6/10 11:47:37

招聘在家抄书员？小心是骗局！！！

在家抄书员的骗局是一种常见的网络诈骗手段&#xff0c;旨在利用人们想要在家轻松赚钱的心理。这种骗局通常会以招聘兼职抄写员的形式出现&#xff0c;声称只需在家中抄写书籍即可赚取可观的收入。然而&#xff0c;实际上这背后隐藏着诸多陷阱和虚假承诺。 首先&#xff0c;这些…...

编程日记 2024/6/10 11:46:36

Pytorch学习11_神经网络-卷积层

1.创建神经网络实例 import torch import torchvision from torch import nn from torch.nn import Conv2d from torch.utils.data import DataLoaderdatasettorchvision.datasets.CIFAR10("../dataset_cov2d",trainFalse,transformtorchvision.transforms.ToTensor(…...

编程日记 2024/6/10 11:45:35

Qt实现程序单实例运行(只能运行1个进程)及QSharedMemory用法

1. 问题提出 在开发时&#xff0c;经常遇到这样的需求或场景&#xff1a;程序只能被启动一次&#xff0c;不能启动多次&#xff0c;启动多次会导致混乱&#xff0c;如&#xff1a;可执行程序用到文件指针、串口句柄等。试想如果存在多个同一个文件的句柄或同一个串口的句柄&…...

编程日记 2024/6/10 11:43:33

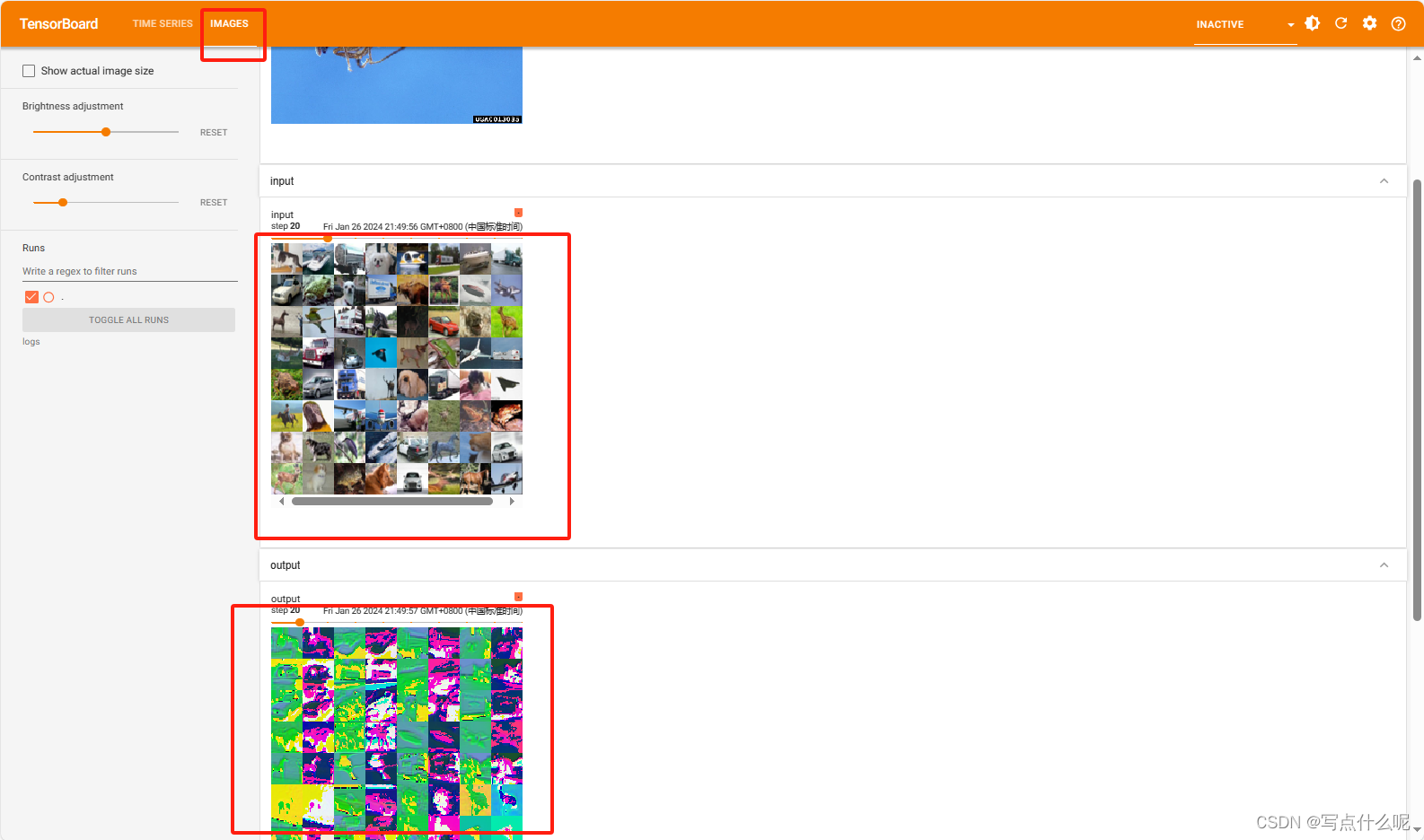
HTTP协议分析实验：通过一次下载任务抓包分析

HTTP协议分析 问&#xff1a;HTTP是干啥用的&#xff1f; 最简单通俗的解释&#xff1a;HTTP 是客户端浏览器或其他程序与Web服务器之间的应用层通信协议。 在Internet上的Web服务器上存放的都是超文本信息&#xff0c;客户机需要通过HTTP协议传输所要访问的超文本信息。 一、…...

编程日记 2024/6/10 11:42:32

http网络服务器

wwwroot(目录)/index.html <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>比特就业课</title>…...

编程日记 2024/6/10 11:41:31

使用C++结合OpenCV进行图像处理与分类

⭐️我叫忆_恒心&#xff0c;一名喜欢书写博客的在读研究生&#x1f468;‍&#x1f393;。 如果觉得本文能帮到您&#xff0c;麻烦点个赞&#x1f44d;呗&#xff01; 近期会不断在专栏里进行更新讲解博客~~~ 有什么问题的小伙伴 欢迎留言提问欧&#xff0c;喜欢的小伙伴给个三…...

编程日记 2024/6/10 11:36:26

探索 Noisee AI 的奇妙世界与变现之旅

日赚800&#xff0c;利用淘宝/闲鱼进行AI音乐售卖实操 如何让AI生成自己喜欢的歌曲-AI音乐创作的正确方式 抖音主播/电商人员有福了&#xff0c;利用Suno创作产品宣传&#xff0c;让产品动起来-小米Su7 用sunoAI写粤语歌的方法&#xff0c;博主已经亲自实践可行 五音不全也…...

编程日记 2024/6/10 11:35:26

【SCSS】use的详细使用规则

目录 use加载成员选择命名空间私有成员配置使用 Mixin重新赋值变量 use 从其他 Sass 样式表中加载 mixins、函数和变量&#xff0c;并将来自多个样式表的 CSS 组合在一起。use加载的样式表被称为“模块”。 加载成员 // src/_corners.scss $radius: 3px;mixin rounded {bord…...

编程日记 2024/6/10 11:33:23

数据结构（C）：二叉树前中后序和层序详解及代码实现及深度刨析

目录 &#x1f31e;0.前言 &#x1f688;1.二叉树链式结构的代码是实现 &#x1f688;2.二叉树的遍历及代码实现和深度刨析代码 &#x1f69d;2.1前序遍历 ✈️2.1.1前序遍历的理解 ✈️2.1.2前序代码的实现 ✈️2.1.3前序代码的深度解剖 &#x1f69d;2.2中序遍历 ✈…...

编程日记 2024/6/10 11:28:18

Win11可以安装AutoCAD2007

1、在win11中&#xff0c;安装AutoCAD2007&#xff0c;需要先安装NET组件。否则会提示缺少".net文件" 打开“控制面板”&#xff0c;点击“程序”&#xff0c;点击“程序和功能”&#xff0c;点击“启用或关闭Windows功能”&#xff0c;勾选“.NET FrameWork 3.5”&a…...

编程日记 2024/6/10 11:27:17

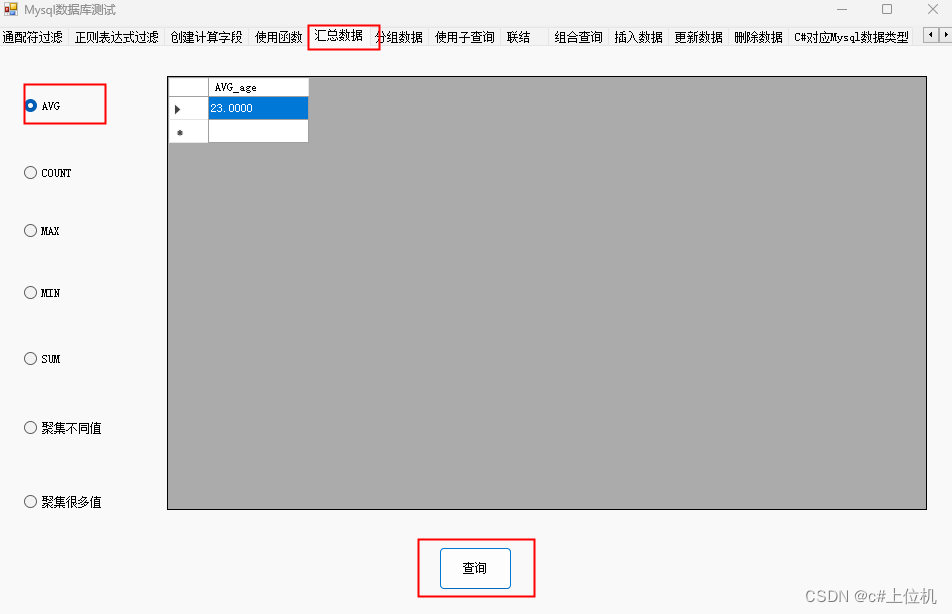
C#操作MySQL从入门到精通(14)——汇总数据

前言 我们有时候需要对数据库查询的值进行一些处理，比如求平均值等操作，本文就是详细讲解这些用法，本文测试使用的数据库数据如下： 1、求平均值 求所有student_age 列的平均值 string sql = string.Empty; if (radioButton_AVG.Checked) {sql = “select AVG( student_…...

编程日记 2024/6/10 11:25:16

【设计模式深度剖析】【2】【行为型】【命令模式】| 以打开文件按钮、宏命令、图形移动与撤销为例加深理解

&#x1f448;️上一篇:模板方法模式 | 下一篇:职责链模式&#x1f449;️ 设计模式-专栏&#x1f448;️ 文章目录 命令模式定义英文原话直译如何理解呢&#xff1f; 四个角色1. Command&#xff08;命令接口&#xff09;2. ConcreteCommand&#xff08;具体命令类&…...

编程日记 2024/6/10 11:24:15

【随手记】maplotlib.use函数设置图像的呈现方式

matplotlib.use() 函数用于设置 matplotlib 的后端&#xff0c;这会影响图形的呈现方式。不同的后端适用于不同的环境和需求。下面列出一些常用的后端及其描述&#xff1a; 常见后端参数 Agg: 参数&#xff1a;agg描述&#xff1a;基于Anti-Grain Geometry的后端&#xff0c;适…...

编程日记 2024/6/10 11:23:14

【kafka】Golang实现分布式Masscan任务调度系统

要求&#xff1a; 输出两个程序&#xff0c;一个命令行程序&#xff08;命令行参数用flag&#xff09;和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽&#xff0c;然后将消息推送到kafka里面。 服务端程序&#xff1a; 从kafka消费者接收…...

编程新知 2026/2/8 20:41:58

STM32+rt-thread判断是否联网

一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

编程新知 2025/9/23 20:06:08

在WSL2的Ubuntu镜像中安装Docker

Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包&#xff1a; for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

编程新知 2026/2/4 16:23:56

Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement

Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement 1. LAB环境2. L2公告策略2.1 部署Death Star2.2 访问服务2.3 部署L2公告策略2.4 服务宣告 3. 可视化 ARP 流量3.1 部署新服务3.2 准备可视化3.3 再次请求 4. 自动IPAM4.1 IPAM Pool4.2 …...

编程新知 2026/2/5 17:29:21

全面解析数据库：从基础概念到前沿应用​

在数字化时代&#xff0c;数据已成为企业和社会发展的核心资产&#xff0c;而数据库作为存储、管理和处理数据的关键工具&#xff0c;在各个领域发挥着举足轻重的作用。从电商平台的商品信息管理&#xff0c;到社交网络的用户数据存储&#xff0c;再到金融行业的交易记录处理&a…...

编程新知 2025/9/19 11:48:17

对象回调初步研究

_OBJECT_TYPE结构分析 在介绍什么是对象回调前&#xff0c;首先要熟悉下结构 以我们上篇线程回调介绍过的导出的PsProcessType 结构为例&#xff0c;用_OBJECT_TYPE这个结构来解析它&#xff0c;0x80处就是今天要介绍的回调链表&#xff0c;但是先不着急&#xff0c;先把目光…...

编程新知 2026/1/26 18:44:47

node.js的初步学习

那什么是node.js呢&#xff1f; 和JavaScript又是什么关系呢&#xff1f; node.js 提供了 JavaScript的运行环境。当JavaScript作为后端开发语言来说&#xff0c; 需要在node.js的环境上进行当JavaScript作为前端开发语言来说&#xff0c;需要在浏览器的环境上进行 Node.js 可…...

编程新知 2025/11/18 1:57:23

AT模式下的全局锁冲突如何解决？

一、全局锁冲突解决方案 1. 业务层重试机制&#xff08;推荐方案&#xff09; Service public class OrderService {GlobalTransactionalRetryable(maxAttempts 3, backoff Backoff(delay 100))public void createOrder(OrderDTO order) {// 库存扣减&#xff08;自动加全…...

编程新知 2026/1/10 0:03:14

分布式光纤声振传感技术原理与瑞利散射机制解析

分布式光纤传感技术&#xff08;Distributed Fiber Optic Sensing&#xff0c;简称DFOS&#xff09;作为近年来迅速发展的新型感知手段&#xff0c;已广泛应用于边界安防、油气管道监测、结构健康诊断、地震探测等领域。其子类技术——分布式光纤声振传感&#xff08;Distribut…...

编程新知 2026/2/6 13:13:32

【见合八方平面波导外腔激光器专题系列】用于干涉光纤传感的低噪声平面波导外腔激光器2

----翻译自Mazin Alalus等人的文章 摘要 1550 nm DWDM 平面波导外腔激光器具有低相位/频率噪声、窄线宽和低 RIN 等特点。该腔体包括一个半导体增益芯片和一个带布拉格光栅的平面光波电路波导&#xff0c;采用 14 引脚蝶形封装。这种平面波导外腔激光器设计用于在振动和恶劣的…...

编程新知 2026/2/5 22:21:59