当前位置： 首页 > news >正文

FiRa标准UWB MAC实现（三）——距离如何获得？

news 2026/2/10 23:02:44

继续前期FiRa MAC相关介绍，将FiRa UWB MAC层相关细节进一步进行剖析，介绍了UWB技术中最重要的一个点，高精度的距离是怎么获得的，具体使用的测距方法都有哪些，原理又是什么。为后续FiRa UWB MAC的实现进行铺垫。

3、测距方法

3.1 SS-TWR

SS-TWR为Single-Sided Two-Way Ranging（SS-TWR，单边双向测距），提供了一种简单的来回测距的方法，通过在协调器与Responder之间消息的往返即可以古迹两个设备之间的飞行时间，进而基于飞行时间估计两个设备之间的距离。

SS-TWR
在实现中，Device B在收到Device A信息之后，发送应答消息，并记录自身的发射时间信息；Device A，收到Device B的接收时间戳，两个设备之间通过记录整个过程中的4个时间戳信息，可以得到 T r o u n d T_{round} Tround​与 T r e p l y T_{reply} Treply​，进而可以得到飞行时间估计，得到两者之间的距离。

T ^ p r o p = 1 2 ( T r o u n d − T r e p l y ) \hat T_{prop} = \frac{1}{2}(T_{round}-T_{reply}) T

相关文章：

FiRa标准UWB MAC实现（三）——距离如何获得？

继续前期FiRa MAC相关介绍，将FiRa UWB MAC层相关细节进一步进行剖析，介绍了UWB技术中最重要的一个点，高精度的距离是怎么获得的，具体使用的测距方法都有哪些，原理又是什么。为后续FiRa UWB MAC的实现进行铺垫。 3、测距方法 3.1 SS-TWR SS-TWR为Single-Sided Two-Way Ra…...

编程日记 2024/6/10 13:54:50

基于百度翻译API的火车头PHP翻译插件，可以翻译HTML片段

关于火车头的百度翻译插件，相信大家在火车头官网或网上都能找到相关代码，百度翻译插件是PHP写的，就一个PHP文件，简单灵活，不受火车头软件版本限制，任何有PHP插件权限的火车头版本都可以使用。但是百度API翻…...

编程日记 2024/6/10 13:52:49

mysql高级用法常用函数

mysql高级用法 1、自定义排序 select * from movies order by field(actors, 成龙, 靳东, 刘亦菲, 范冰冰); // 字段中存在null值 select * from movies order by field (coalesce(actors,null),成龙, 靳东, 刘亦菲, 范冰冰,null)2、空值NULL排序（ORDER BY IF(ISN…...

编程日记 2024/6/10 13:51:48

【打印100个常用Linux命令】

#!/bin/bash 定义一个函数，用于打印100个常用Linux命令 print_commands() { echo “以下是一些常用的Linux命令：” echo “----------------------------------” echo “1. pwd - 显示当前工作目录” echo “2. ls - 列出当前目录下的文件和文件夹” …...

编程日记 2024/6/10 13:49:46

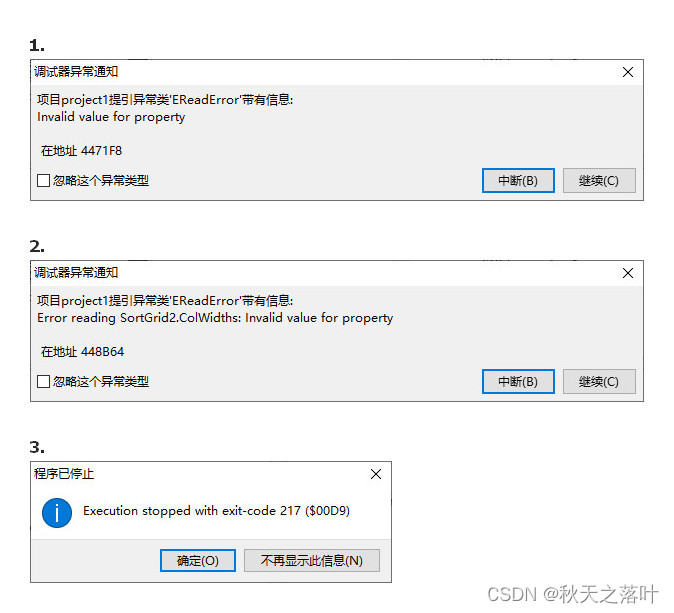
友情提示：lazarus的tsortgrid.autofillcolumns存在BUG

直接在tsortgrid的属性中设置autofillcolumns为true，会提示：123个错误。即使修改为false，编译运行照样会出现上述错误。唯一解决的办法就是删除sortgrid重新添加一个。 代码设置SortGrid1.AutoFillColumns : TRUE不受影响。...

编程日记 2024/6/10 13:48:45

github的个人readme文件

一个好的svg图: Simon-He95/profile-3d-contrib/profile-season-animate.svg at 4281d9f46e3d5416bd8f8cc5779157bfdaa8589d Simon-He95/Simon-He95 GitHub 请访问他的主页从提交记录就可以看到这个立体的登录github的图...

编程日记 2024/6/10 13:42:39

java面试题： HashMap、HashSet 和 HashTable 的区别

HashMap 常用方法 HashMap 是一个基于哈希表的 Map 接口的实现。它允许使用 null 值和 null 键。 java 复制 // 创建一个HashMap HashMap<KeyType, ValueType> map new HashMap<>(); // 添加元素 map.put(key, value); // 获取元素 ValueType value map.get…...

编程日记 2024/6/10 13:41:38

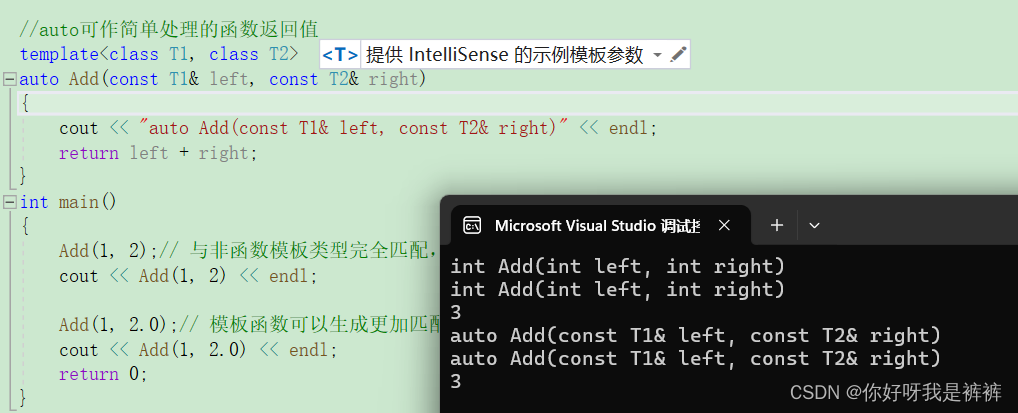
CPP初级：模板的运用！

目录 一.泛型编程 二.函数模板 1.函数模板概念 2.函数模板格式 3.函数模板的原理 三.函数模板的实例化 1.隐式实例化 2.显式实例化 3.模板参数的匹配原则 四.类模板 1.类模板的定义格式 2.类模板的实例化 一.泛型编程 泛型编程&#xff1a;编写与类型无关的通用代码…...

编程日记 2024/6/10 13:40:37

排序---基数排序

前言 个人小记 一、简介 基数排序是一种非比较排序&#xff0c;所以排序速度较快&#xff0c;当为32位int整数排序时&#xff0c;可以将数分为个位十位分别为2^16,使得拷贝只需要两轮&#xff0c;从而达到2*n&#xff0c;然后给一个偏移量&#xff0c;使得可以对负数排序。以…...

编程日记 2024/6/10 13:39:36

“新高考”下分班怎么分？

来自安徽的张女士告诉我&#xff1a;上一年孩子升入了高中&#xff0c;但没想到才高一&#xff0c;孩子就面临了一个困难的挑选&#xff1a;312”分班&#xff01; 什么是312”分班呢&#xff1f;许多人或许不明白&#xff0c;便是要求学生在高一入学时&#xff0c;针对于3门必…...

编程日记 2024/6/10 13:38:36

二叉树的层序遍历-力扣

本题是二叉树的层序遍历&#xff0c;通过一个队列来控制遍历的节点&#xff0c;二叉树每层的节点和上一层入队的节点个数是相同的&#xff0c;根据这一点编写循环条件。 /*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* …...

编程日记 2024/6/10 13:37:35

N32G45XVL-STB之移植LVGL(lvgl-8.2.0)

目录 概述 1 软硬件介绍 1.1 软件版本信息 1.2 ST7796-LCD 1.3 MCU IO与LCD PIN对应关系 2 认识LVGL 2.1 LVGL官网 2.2 LVGL库文件下载 3 移植LVGL 3.1 准备移植文件 3.2 添加lvgl库文件到项目 3.2.1 src下的文件 3.2.2 examples下的文件 3.2.3 配置文件路径 3.2…...

编程日记 2024/6/10 13:34:31

【设计模式】创建型设计模式之 原型模式

介绍 原型模式是一种创建型设计模式&#xff0c;主要用于创建重复的对象&#xff0c;而无需重新初始化它们&#xff0c;从而提高效率并简化对象的创建过程。此模式的核心思想是利用已存在的对象实例&#xff0c;通过复制&#xff08;克隆&#xff09;的方式来生成新的对象&…...

编程日记 2024/6/10 13:33:30

【类型商店】字符字符串（下）

啊&#xff0c;哈喽&#xff0c;小伙伴们大家好。我是#Y清墨&#xff0c;今天呐&#xff0c;我要介绍的是字符与字符串。 导语 前两期&#xff0c;我们已经懂得了概念&#xff0c;今天来看些函数。 正题 一.增加或连接 &#xff08;1) 后面增加() string s1,s2; //定义 s…...

编程日记 2024/6/10 13:32:29

『 Linux 』内存管理与文件系统

文章目录 交换分区页与页框(页帧)交换分区与内存之间的交换操作系统如何管理内存物理地址转换页号与页内偏移量 内存管理,文件系统与文件管理之间的联系 交换分区 在Linux的安装过程中,用户将会被提示创建一个交换分区; 这是一个特殊的分区,其大小可以由用户根据系统内存需求和…...

编程日记 2024/6/10 13:28:23

线性代数|机器学习-P8矩阵低秩近似eckart-young

文章目录 1. SVD奇异值分解2. Eckart-Young2.1 范数 3. Q A Q U Σ V T QAQU\Sigma V^T QAQUΣVT4. 主成分分析图像表示 1. SVD奇异值分解 我们知道&#xff0c;对于任意矩阵A来说&#xff0c;我们可以将其通过SVD奇异值分解得到 A U Σ V T AU\Sigma V^T AUΣVT&#xff0…...

编程日记 2024/6/10 13:25:18

平面设计神器CorelDRAW2021精简版，你值得拥有！

亲爱的设计师小伙伴们&#xff0c;今天我要为大家种草一款神奇的软件——CorelDRAW平面设计软件2021精简版&#xff01;&#x1f929;✨作为一名专业的图形设计师&#xff0c;我深知一个好工具对于我们的工作有多么重要。而这款软件简直就是我们设计师的救星&#xff01;&#…...

编程日记 2024/6/10 13:22:15

kafka是什么？

Kafka是一个由Apache软件基金会开发的开源流处理平台&#xff0c;最初由LinkedIn公司开发&#xff0c;使用Scala和Java编写。它是一个高吞吐量的分布式发布订阅消息系统&#xff0c;可以处理消费者在网站中的所有动作流数据&#xff0c;如网页浏览、搜索和其他用户行为等。Kafk…...

编程日记 2024/6/10 13:21:14

ABC351

C 栈的应用 #include<bits/stdc.h>using namespace std;stack<int>stk;int main() {int n;cin>>n;for(int i1;i<n;i){int a;cin>>a;while(!stk.empty()&&astk.top()){stk.pop();a;}stk.push(a);}cout<<stk.size()<<endl;retur…...

编程日记 2024/6/10 13:20:12

base上海，数据科学，数据挖掘，数据分析等岗位求收留

裁员了&#xff0c;base上海&#xff0c;数据科学&#xff0c;数据挖掘&#xff0c;数据分析等岗位&#xff0c;期望30k~40k&#xff0c;求推荐求收留 1&#xff0c;6年数据算法工作&#xff0c;做过指标体系搭建&#xff0c;用户画像&#xff0c;货品定价&#xff0c;社区分析…...

编程日记 2024/6/10 13:18:10

日语AI面试高效通关秘籍：专业解读与青柚面试智能助攻

在如今就业市场竞争日益激烈的背景下&#xff0c;越来越多的求职者将目光投向了日本及中日双语岗位。但是&#xff0c;一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧&#xff1f;面对生疏的日语交流环境&#xff0c;即便提前恶补了…...

编程新知 2026/2/8 4:37:01

深入剖析AI大模型：大模型时代的 Prompt 工程全解析

今天聊的内容&#xff0c;我认为是AI开发里面非常重要的内容。它在AI开发里无处不在&#xff0c;当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗"&#xff0c;或者让翻译模型 "将这段合同翻译成商务日语" 时&#xff0c;输入的这句话就是 Prompt。…...

编程新知 2026/2/8 20:42:53

云计算——弹性云计算器（ECS）

弹性云服务器&#xff1a;ECS 概述 云计算重构了ICT系统&#xff0c;云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台&#xff0c;包含如下主要概念。 ECS&#xff08;Elastic Cloud Server&#xff09;&#xff1a;即弹性云服务器&#xff0c;是云计算…...

编程新知 2025/8/16 21:50:27

SciencePlots——绘制论文中的图片

文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了&#xff1a;一行…...

编程新知 2025/9/8 13:50:07

边缘计算医疗风险自查APP开发方案

核心目标：在便携设备（智能手表/家用检测仪）部署轻量化疾病预测模型，实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

编程新知 2026/2/10 13:18:55

FFmpeg 低延迟同屏方案

引言 在实时互动需求激增的当下&#xff0c;无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作&#xff0c;还是游戏直播的画面实时传输&#xff0c;低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架&#xff0c;凭借其灵活的编解码、数据…...

编程新知 2025/11/4 6:26:59

vue3 字体颜色设置的多种方式

在Vue 3中设置字体颜色可以通过多种方式实现&#xff0c;这取决于你是想在组件内部直接设置&#xff0c;还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法&#xff1a; 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

编程新知 2026/2/4 20:47:44

反射获取方法和属性

Java反射获取方法 在Java中&#xff0c;反射&#xff08;Reflection&#xff09;是一种强大的机制&#xff0c;允许程序在运行时访问和操作类的内部属性和方法。通过反射&#xff0c;可以动态地创建对象、调用方法、改变属性值&#xff0c;这在很多Java框架中如Spring和Hiberna…...

编程新知 2025/11/9 2:57:17

C# 类和继承(抽象类)

抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

编程新知 2026/1/29 16:25:24

2025盘古石杯决赛【手机取证】

前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来&#xff0c;实在找不到&#xff0c;希望有大佬教一下我。 还有就会议时间&#xff0c;我感觉不是图片时间&#xff0c;因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

编程新知 2026/1/29 17:12:17