排序---基数排序
前言
个人小记
一、简介
基数排序是一种非比较排序,所以排序速度较快,当为32位int整数排序时,可以将数分为个位十位分别为2^16,使得拷贝只需要两轮,从而达到2*n,然后给一个偏移量,使得可以对负数排序。以下是一个非正确(自以为正确)的基数排序优化和未优化的比较。(注意:这可是对1000万的数据排序!前几个排序都是10万的数据!)
二、代码
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <time.h>
#define MAX_ARR 10000000
#define swap(a,b)\
{\__typeof(a) __c=a;\a=b,b=__c;\
}
#define TEST(func,arr,l,r)\
{\printf("test:%s \t",#func);\int n=r-l;\int* t=(int*)malloc(sizeof(int)*n);\long long a=clock();\func(t,l,r);\long long b=clock();\if(check(t,n))printf("OK %lldms\n",(b-a)*1000/CLOCKS_PER_SEC);\else printf("FAIL\n");\free(t);\
}int check(int *t,int n)
{for(int i=1;i<n;i++){if(t[i-1]>t[i])return 0;}return 1;
}int * init_arr(int n)
{int*arr=(int*)malloc(sizeof(int)*n);for(int i=0;i<n;i++){if(rand()%2)arr[i]=-rand()%10000000;else arr[i]=rand()%10000000;}return arr;
}
int *cont,*temp;
void PO_radix_sort(int *arr,int l,int r)
{int k=65536;//2^16memset(cont,0,sizeof(int)*k*2);for(int i=l;i<r;i++){if(arr[i]<0)cont[k+abs(arr[i]%k)]++;//理论个位else cont[arr[i]%k]++;}for(int i=1;i<k;i++)cont[i]=cont[i-1]+cont[i];for(int i=r-1;i>=l;i--){if(arr[i]<0)temp[--cont[abs(arr[i]%k)]]=arr[i];else temp[--cont[arr[i]%k]]=arr[i];}memcpy(arr+l,temp,sizeof(int)*(r-l));memset(cont,0,sizeof(int)*k*2);for(int i=l;i<r;i++){if(arr[i]<0)cont[k+abs(arr[i]/k)]++;//理论十位else cont[arr[i]/k]++;}for(int i=1;i<k;i++)cont[i]=cont[i-1]+cont[i];for(int i=r-1;i>=l;i--){if(arr[i]<0)temp[--cont[abs(arr[i]/k)]]=arr[i];else temp[--cont[arr[i]/k]]=arr[i];}memcpy(arr+l,temp,sizeof(int)*(r-l));return ;
}
void radix_sort(int *arr,int l,int r)
{int k=65536;//2^16int *cont_1=(int *)malloc(sizeof(int)*k*2);int *temp_1=(int *)malloc(sizeof(int)*(r-l));memset(cont_1,0,sizeof(int)*k*2);for(int i=l;i<r;i++){if(arr[i]<0)cont_1[k+abs(arr[i]%k)]++;//理论个位else cont_1[arr[i]%k]++;}for(int i=1;i<k;i++)cont_1[i]=cont_1[i-1]+cont_1[i];for(int i=r-1;i>=l;i--){if(arr[i]<0)temp_1[--cont_1[abs(arr[i]%k)]]=arr[i];else temp_1[--cont_1[arr[i]%k]]=arr[i];}memcpy(arr+l,temp_1,sizeof(int)*(r-l));memset(cont_1,0,sizeof(int)*k*2);for(int i=l;i<r;i++){if(arr[i]<0)cont_1[k+abs(arr[i]/k)]++;//理论十位else cont_1[arr[i]/k]++;}for(int i=1;i<k;i++)cont_1[i]=cont_1[i-1]+cont_1[i];for(int i=r-1;i>=l;i--){if(arr[i]<0)temp_1[--cont_1[abs(arr[i]/k)]]=arr[i];else temp_1[--cont_1[arr[i]/k]]=arr[i];}memcpy(arr+l,temp_1,sizeof(int)*(r-l));free(cont_1);free(temp_1);return ;
}int main()
{srand((unsigned)time(0));int *arr=init_arr(MAX_ARR);cont=(int*)malloc(sizeof(int)*65536*2);temp=(int *)malloc(sizeof(int)*MAX_ARR);TEST(radix_sort,arr,0,MAX_ARR); TEST(PO_radix_sort,arr,0,MAX_ARR); free(arr);free(cont);free(temp);return 0;
}
三、测试结果
test:radix_sort OK 284ms
test:PO_radix_sort OK 302ms
四、优化错误原因
1.内存局部性: radix_sort 在每次调用时都会分配新的内存,这可能意味着它使用的内存更有可能在CPU的缓存中,因为它是最近分配的。相比之下,PO_radix_sort 使用的是预先分配的全局数组,这些数组可能不在缓存中,尤其是在程序运行了其他代码之后。内存局部性差可能导致更多的缓存未命中,从而降低性能。
2.内存碎片: 如果程序在调用 PO_radix_sort 之前已经运行了一段时间,全局数组可能会在物理内存中分散开来,这增加了内存访问的开销。而 radix_sort 动态分配的内存更有可能是连续的,这有助于提高访问速度。
3.编译器优化: 动态分配的内存可能使得编译器能够更好地优化 radix_sort 函数,因为编译器知道这些内存是局部的,并且其生命周期仅限于函数调用。全局变量通常更难以优化,因为它们必须在整个程序的生命周期内保持有效。
4.多次函数调用: 如果 TEST 宏多次调用 PO_radix_sort,全局数组 cont 和 temp 不会在每次调用之间清除或重新初始化,这可能导致性能下降。而 radix_sort 每次调用都会得到新的内存,这确保了每次排序都是从一个干净的状态开始的。
5.内存分配策略: 操作系统的内存分配策略可能也会影响性能。例如,某些系统可能会更快地分配大块内存,而其他系统可能在处理多个小的分配时更有效率。
相关文章:

排序---基数排序
前言 个人小记 一、简介 基数排序是一种非比较排序,所以排序速度较快,当为32位int整数排序时,可以将数分为个位十位分别为2^16,使得拷贝只需要两轮,从而达到2*n,然后给一个偏移量,使得可以对负数排序。以…...
“新高考”下分班怎么分?
来自安徽的张女士告诉我:上一年孩子升入了高中,但没想到才高一,孩子就面临了一个困难的挑选:312”分班! 什么是312”分班呢?许多人或许不明白,便是要求学生在高一入学时,针对于3门必…...

二叉树的层序遍历-力扣
本题是二叉树的层序遍历,通过一个队列来控制遍历的节点,二叉树每层的节点和上一层入队的节点个数是相同的,根据这一点编写循环条件。 /*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* …...

N32G45XVL-STB之移植LVGL(lvgl-8.2.0)
目录 概述 1 软硬件介绍 1.1 软件版本信息 1.2 ST7796-LCD 1.3 MCU IO与LCD PIN对应关系 2 认识LVGL 2.1 LVGL官网 2.2 LVGL库文件下载 3 移植LVGL 3.1 准备移植文件 3.2 添加lvgl库文件到项目 3.2.1 src下的文件 3.2.2 examples下的文件 3.2.3 配置文件路径 3.2…...

【设计模式】创建型设计模式之 原型模式
介绍 原型模式是一种创建型设计模式,主要用于创建重复的对象,而无需重新初始化它们,从而提高效率并简化对象的创建过程。此模式的核心思想是利用已存在的对象实例,通过复制(克隆)的方式来生成新的对象&…...

【类型商店】字符字符串(下)
啊,哈喽,小伙伴们大家好。我是#Y清墨,今天呐,我要介绍的是字符与字符串。 导语 前两期,我们已经懂得了概念,今天来看些函数。 正题 一.增加或连接 (1) 后面增加() string s1,s2; //定义 s…...

『 Linux 』内存管理与文件系统
文章目录 交换分区页与页框(页帧)交换分区与内存之间的交换操作系统如何管理内存物理地址转换页号与页内偏移量 内存管理,文件系统与文件管理之间的联系 交换分区 在Linux的安装过程中,用户将会被提示创建一个交换分区; 这是一个特殊的分区,其大小可以由用户根据系统内存需求和…...

线性代数|机器学习-P8矩阵低秩近似eckart-young
文章目录 1. SVD奇异值分解2. Eckart-Young2.1 范数 3. Q A Q U Σ V T QAQU\Sigma V^T QAQUΣVT4. 主成分分析图像表示 1. SVD奇异值分解 我们知道,对于任意矩阵A来说,我们可以将其通过SVD奇异值分解得到 A U Σ V T AU\Sigma V^T AUΣVT࿰…...

平面设计神器CorelDRAW2021精简版,你值得拥有!
亲爱的设计师小伙伴们,今天我要为大家种草一款神奇的软件——CorelDRAW平面设计软件2021精简版!🤩✨作为一名专业的图形设计师,我深知一个好工具对于我们的工作有多么重要。而这款软件简直就是我们设计师的救星!&#…...

kafka是什么?
Kafka是一个由Apache软件基金会开发的开源流处理平台,最初由LinkedIn公司开发,使用Scala和Java编写。它是一个高吞吐量的分布式发布订阅消息系统,可以处理消费者在网站中的所有动作流数据,如网页浏览、搜索和其他用户行为等。Kafk…...

ABC351
C 栈的应用 #include<bits/stdc.h>using namespace std;stack<int>stk;int main() {int n;cin>>n;for(int i1;i<n;i){int a;cin>>a;while(!stk.empty()&&astk.top()){stk.pop();a;}stk.push(a);}cout<<stk.size()<<endl;retur…...

base上海,数据科学,数据挖掘,数据分析等岗位求收留
裁员了,base上海,数据科学,数据挖掘,数据分析等岗位,期望30k~40k,求推荐求收留 1,6年数据算法工作,做过指标体系搭建,用户画像,货品定价,社区分析…...

IC元器件
1.电阻: 电阻的作用: 1.与负载串联:做限流分压 2.电阻并联:将小功率电阻并联成大功率,防烧毁 2.电容: 电容就是两块金属板+中间的介质(相当于两个人坐在一起加上中间的空气…...

SQL159 每个创作者每月的涨粉率及截止当前的总粉丝量
描述 用户-视频互动表tb_user_video_log iduidvideo_idstart_timeend_timeif_followif_likeif_retweetcomment_id110120012021-09-01 10:00:002021-09-01 10:00:20011NULL210520022021-09-10 11:00:002021-09-10 11:00:30101NULL310120012021-10-01 10:00:002021-10-01 10:00…...
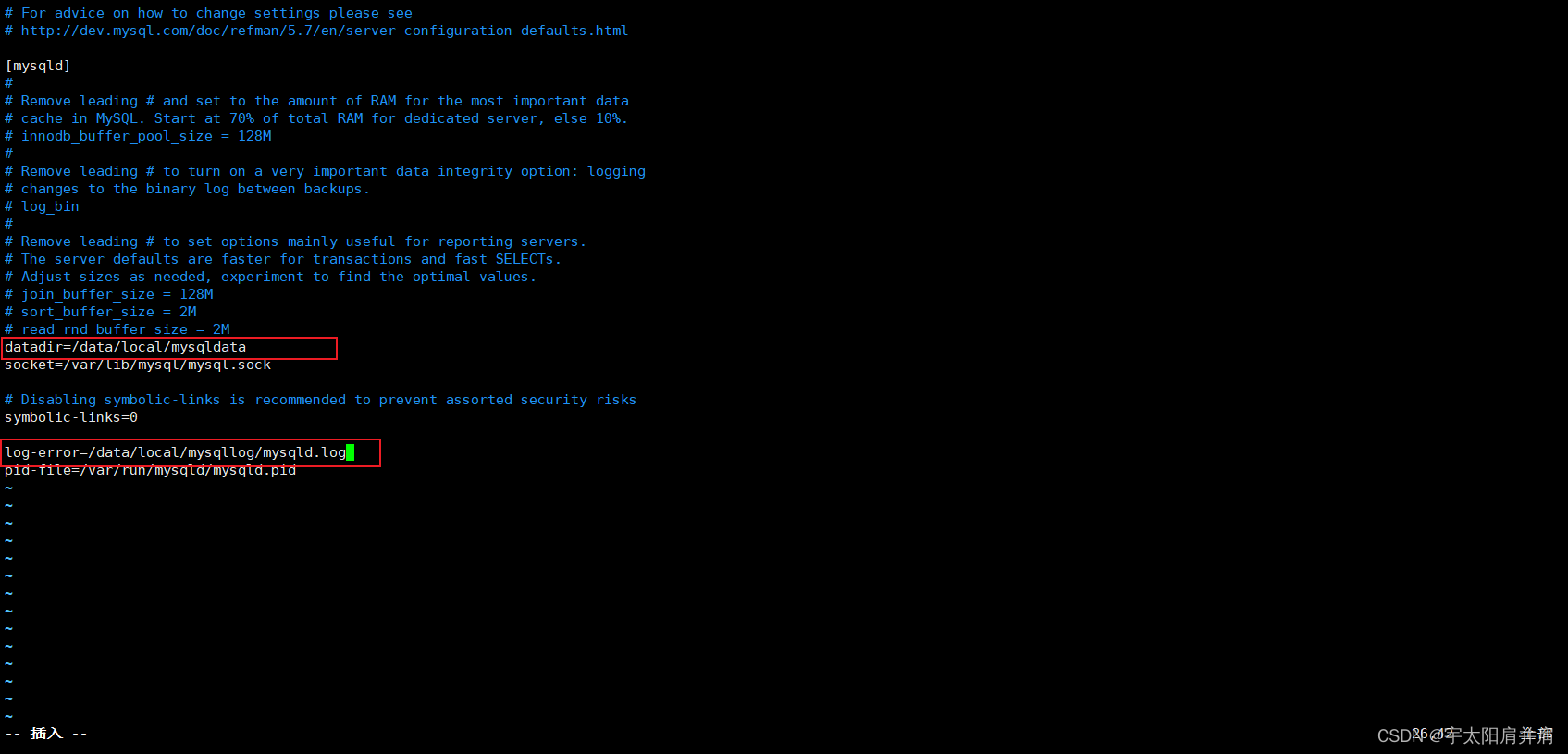
Linux安装MySQL教程【带图文命令巨详细】
巨详细Linux安装MySQL 1、查看是否有自带数据库或残留数据库信息1.1检查残留mysql1.2检查并删除残留mysql依赖1.3检查是否自带mariadb库 2、下载所需MySQL版本,上传至系统指定位置2.1创建目录2.2下载MySQL压缩包 3、安装MySQL3.1创建目录3.2解压mysql压缩包3.3安装解…...
外部排序快速入门详解:基本原理,败者树,置换-选择排序,最佳归并树
文章目录 外部排序1.最基本的外部排序原理2.外部排序的优化2.1 败者树优化方法2.2 置换-选择排序优化方法2.3 最佳归并树 外部排序 为什么要学习外部排序? 答: 在处理数据的过程中,我们需要把磁盘(外存)中存储的数据拿到内存中处理…...

人工智能和物联网如何结合
欢迎来到 Papicatch的博客 目录 🍉引言 🍉AI与IoT的结合方式 🍈数据处理和分析 🍍实例 🍈边缘计算 🍍实例 🍈自动化和自主操作 🍍实例 🍈安全和隐私保护 &…...

【JAVASE】JAVA应用案例(下)
一:抢红包 一个大V直播时,发起了抢红包活动,分别有9,666,188,520,99999五个红包。请模拟粉丝来抽奖,按照先来先得,随机抽取,抽完即止,注意:一个红包只能被抽一次,先抽或…...

【面试干货】 B 树与 B+ 树的区别
【面试干货】 B 树与 B 树的区别 1、B 树2、 B 树3、 区别与优缺点比较4、 总结 💖The Begin💖点点关注,收藏不迷路💖 在数据库系统中,B 树和 B 树是常见的索引结构,它们在存储和组织数据方面有着不同的设计…...

Socket编程权威指南(四)彻底解密 Epoll 原理
在上一篇文章中,我们优化了基于 Socket 的网络服务器,从最初的 select/poll 模型进化到了高效的 epoll。很多读者对 epoll 的惊人性能表示极大的兴趣,对它的工作原理也充满了好奇。今天,就让我们一起揭开 epoll 神秘的面纱&#x…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...
