线性代数|机器学习-P8矩阵低秩近似eckart-young
文章目录
- 1. SVD奇异值分解
- 2. Eckart-Young
- 2.1 范数
- 3. Q A = Q U Σ V T QA=QU\Sigma V^T QA=QUΣVT
- 4. 主成分分析图像表示
1. SVD奇异值分解
我们知道,对于任意矩阵A来说,我们可以将其通过SVD奇异值分解得到 A = U Σ V T A=U\Sigma V^T A=UΣVT,通过 Σ \Sigma Σ中可以看到只有r个非零的特征值,所以通过矩阵A奇异值分解可得如下表达式:
A = σ 1 u 1 v 1 T + σ 2 u 2 v 2 T + ⋯ + σ n u n v n T , σ 1 ≥ σ 2 ≥ ⋯ ≥ σ r \begin{equation} A=\sigma_1u_1v_1^T+\sigma_2u_2v_2^T+\cdots+\sigma_nu_nv_n^T,\sigma_1\geq \sigma_2\geq\cdots\geq\sigma_r \end{equation} A=σ1u1v1T+σ2u2v2T+⋯+σnunvnT,σ1≥σ2≥⋯≥σr
A k = σ 1 u 1 v 1 T + σ 2 u 2 v 2 T + ⋯ + σ k u k v k T , σ 1 ≥ σ 2 ≥ ⋯ ≥ σ k \begin{equation} A_k=\sigma_1u_1v_1^T+\sigma_2u_2v_2^T+\cdots+\sigma_ku_kv_k^T,\sigma_1\geq \sigma_2\geq\cdots\geq\sigma_k \end{equation} Ak=σ1u1v1T+σ2u2v2T+⋯+σkukvkT,σ1≥σ2≥⋯≥σk
A ∼ A k \begin{equation} A\sim A_k \end{equation} A∼Ak
- 上面的等式里面,我们希望通过前面k项的和来近似矩阵A,这就是
主成分分析PCA
2. Eckart-Young
如果矩阵B的秩为 k ,对于矩阵A和B的距离来说,矩阵A与子矩阵 A k A_k Ak(秩为k)的距离小于等于矩阵A与矩阵B之间的距离

- 假设我们有如下矩阵
A = [ 4 0 0 0 0 3 0 0 0 0 2 0 0 0 0 1 ] ; A 2 = [ 4 0 0 0 0 3 0 0 0 0 0 0 0 0 0 0 ] ; B = [ 3.5 3.5 0 0 3.5 3.5 0 0 0 0 1.5 1.5 0 0 1.5 1.5 ] \begin{equation} A=\begin{bmatrix} 4&0&0&0\\\\ 0&3&0&0\\\\ 0&0&2&0\\\\ 0&0&0&1 \end{bmatrix};A_2=\begin{bmatrix} 4&0&0&0\\\\ 0&3&0&0\\\\ 0&0&0&0\\\\ 0&0&0&0 \end{bmatrix};B=\begin{bmatrix} 3.5&3.5&0&0\\\\ 3.5&3.5&0&0\\\\ 0&0&1.5&1.5\\\\ 0&0&1.5&1.5 \end{bmatrix} \end{equation} A= 4000030000200001 ;A2= 4000030000000000 ;B= 3.53.5003.53.500001.51.5001.51.5 - 用python计算 ∣ ∣ A − B ∣ ∣ ≥ ∣ ∣ A − A k ∣ ∣ ||A-B||\geq ||A-A_k|| ∣∣A−B∣∣≥∣∣A−Ak∣∣
import numpy as npif __name__=="__main__":A=np.array([ [4,0,0,0],[0,3,0,0],[0,0,2,0],[0,0,0,1]],dtype='int16')A2=np.array([ [4,0,0,0],[0,3,0,0],[0,0,0,0],[0,0,0,0]],dtype='int16')B=np.array([ [3.5,3.5,0,0],[3.5,3.5,0,0],[0,0,1.5,1.5],[0,0,1.5,1.5]],dtype='int16')Aa2norm =A-A2AB2norm =A-Bprint(f"A={A}")print(f"A2={A2}")print(f"B={B}")print(f"Aa2norm={np.linalg.norm(Aa2norm,ord=2)}")print(f"AB2norm={np.linalg.norm(AB2norm,ord=2)}")
#A=[[4 0 0 0]
# [0 3 0 0]
# [0 0 2 0]
# [0 0 0 1]]
#A2=[[4 0 0 0]
# [0 3 0 0]
# [0 0 0 0]
# [0 0 0 0]]
#B=[[3 3 0 0]
# [3 3 0 0]
# [0 0 1 1]
# [0 0 1 1]]
#Aa2norm=2.0
#AB2norm=3.54138126514911
- 结果: ∣ ∣ A − B ∣ ∣ 2 = 3.54 , ∣ ∣ A − A 2 ∣ ∣ = 2.0 → ∣ ∣ A − B ∣ ∣ ≥ ∣ ∣ A − A 2 ∣ ∣ ||A-B||_2=3.54,||A-A_2||=2.0\rightarrow ||A-B||\geq||A-A_2|| ∣∣A−B∣∣2=3.54,∣∣A−A2∣∣=2.0→∣∣A−B∣∣≥∣∣A−A2∣∣
- 向量x乘以正交单位矩阵Q后长度不变,正交矩阵相当于将向量旋转,所以长度不变。
∣ ∣ x ∣ ∣ 2 = x T x = x T Q T Q x = ( Q x ) T Q x = ∣ ∣ Q x ∣ ∣ 2 \begin{equation} ||x||_2=x^Tx=x^TQ^TQx=(Qx)^TQx=||Qx||_2 \end{equation} ∣∣x∣∣2=xTx=xTQTQx=(Qx)TQx=∣∣Qx∣∣2
这就是主成分分析的原理,因为矩阵A里面有很多无用信息,用 A k A_k Ak 来代替 A
2.1 范数
-
向量 L 1 L_1 L1范数
∣ ∣ V ∣ ∣ 1 = ∣ v 1 ∣ + ∣ v 2 ∣ + ⋯ + ∣ v n ∣ \begin{equation} ||V||_1=|v_1|+|v_2|+\cdots+|v_n| \end{equation} ∣∣V∣∣1=∣v1∣+∣v2∣+⋯+∣vn∣ -
向量 L 2 L_2 L2范数
∣ ∣ V ∣ ∣ 2 = v 1 2 + v 2 2 + ⋯ + v n 2 \begin{equation} ||V||_2=\sqrt{v_1^2+v_2^2+\cdots+v_n^2} \end{equation} ∣∣V∣∣2=v12+v22+⋯+vn2 -
向量 L ∞ L_{\infty} L∞范数
∣ ∣ V ∣ ∣ ∞ = m a x ∣ v i ∣ \begin{equation} ||V||_{\infty}=\mathrm{max}|v_i| \end{equation} ∣∣V∣∣∞=max∣vi∣ -
我们假设在二维平面上,我们就三个范数进行图形形象表达:


-
小结,随着范数越大,图形由原来的菱形膨胀到了正方形,这个正方形就是极限了。这个思路真神奇!!!
-
L 1 L_1 L1函数范数跟向量 L 1 L_1 L1范数一样,通过 L 1 L_1 L1函数可以知道一个函数在指定区间内的体量 L 1 L_1 L1函数范数
L = ∑ i = 1 n ∣ y i − f ( x i ) ∣ \begin{equation} L=\sum_{i=1}^n|y_i-f(x_i)| \end{equation} L=i=1∑n∣yi−f(xi)∣ -
L 2 L_2 L2函数范数
L 2 L_2 L2损失函数表示测量和真实值之差的平方,就是我们之前一直用的最小二乘法。真神奇,居然都对上了,同一个问题,不同的角度。
L = ∑ i = 1 n ( y i − f ( x i ) ) 2 \begin{equation} L=\sum_{i=1}^n(y_i-f(x_i))^2 \end{equation} L=i=1∑n(yi−f(xi))2
矩阵 L 1 L_1 L1范数定义为每一列元素绝对值之和的最大值。具体步骤是:
1. 对矩阵A的每一列,求每个元素的绝对值之和
2. 找出所有列和中最大值 -
L 2 L_2 L2矩阵范数定义为矩阵A的最大奇异值,计算步骤:
1. 计算矩阵A的共轭转置,记为 A H A^H AH,得到 A H A , A A H A^HA,AA^H AHA,AAH
2. 计算矩阵 A A H , A H A AA^H,A^HA AAH,AHA的特征值,求出平方根后求得最大特征值为 L 2 L_2 L2范数 -
Frobenius-norm
∣ ∣ A ∣ ∣ F = σ 1 2 + σ 2 2 + ⋯ + σ r 2 \begin{equation} ||A||_F=\sqrt{\sigma_1^2+\sigma_2^2+\cdots+\sigma_r^2} \end{equation} ∣∣A∣∣F=σ12+σ22+⋯+σr2 -
Nuclear-norm
∣ ∣ A ∣ ∣ N = σ 1 + σ 2 + ⋯ + σ r \begin{equation} ||A||_N=\sigma_1+\sigma_2+\cdots+\sigma_r \end{equation} ∣∣A∣∣N=σ1+σ2+⋯+σr
3. Q A = Q U Σ V T QA=QU\Sigma V^T QA=QUΣVT
对于矩阵A来说,我们可以左乘以一个正交单位矩阵A,其特征值不变
Q A = ( Q U ) Σ V T \begin{equation} QA=(QU)\Sigma V^T \end{equation} QA=(QU)ΣVT
4. 主成分分析图像表示
我们来看看最小二乘法的图像,通过求y方向的最小值和来拟合曲线
L = ∑ i = 1 n ∣ y i − f ( x i ) ∣ → A T A x ^ = A T b → x ^ = ( A T A ) − 1 A T b \begin{equation} L=\sum_{i=1}^n|y_i-f(x_i)|\rightarrow A^TA\hat{x}=A^Tb\rightarrow \hat{x}=(A^TA)^{-1}A^Tb \end{equation} L=i=1∑n∣yi−f(xi)∣→ATAx^=ATb→x^=(ATA)−1ATb

- 主成分分析PCA 是通过先减去样本的均值后,根据点到直线的垂直距离来拟合直线。
相关文章:

线性代数|机器学习-P8矩阵低秩近似eckart-young
文章目录 1. SVD奇异值分解2. Eckart-Young2.1 范数 3. Q A Q U Σ V T QAQU\Sigma V^T QAQUΣVT4. 主成分分析图像表示 1. SVD奇异值分解 我们知道,对于任意矩阵A来说,我们可以将其通过SVD奇异值分解得到 A U Σ V T AU\Sigma V^T AUΣVT࿰…...

平面设计神器CorelDRAW2021精简版,你值得拥有!
亲爱的设计师小伙伴们,今天我要为大家种草一款神奇的软件——CorelDRAW平面设计软件2021精简版!🤩✨作为一名专业的图形设计师,我深知一个好工具对于我们的工作有多么重要。而这款软件简直就是我们设计师的救星!&#…...

kafka是什么?
Kafka是一个由Apache软件基金会开发的开源流处理平台,最初由LinkedIn公司开发,使用Scala和Java编写。它是一个高吞吐量的分布式发布订阅消息系统,可以处理消费者在网站中的所有动作流数据,如网页浏览、搜索和其他用户行为等。Kafk…...

ABC351
C 栈的应用 #include<bits/stdc.h>using namespace std;stack<int>stk;int main() {int n;cin>>n;for(int i1;i<n;i){int a;cin>>a;while(!stk.empty()&&astk.top()){stk.pop();a;}stk.push(a);}cout<<stk.size()<<endl;retur…...

base上海,数据科学,数据挖掘,数据分析等岗位求收留
裁员了,base上海,数据科学,数据挖掘,数据分析等岗位,期望30k~40k,求推荐求收留 1,6年数据算法工作,做过指标体系搭建,用户画像,货品定价,社区分析…...

IC元器件
1.电阻: 电阻的作用: 1.与负载串联:做限流分压 2.电阻并联:将小功率电阻并联成大功率,防烧毁 2.电容: 电容就是两块金属板+中间的介质(相当于两个人坐在一起加上中间的空气…...

SQL159 每个创作者每月的涨粉率及截止当前的总粉丝量
描述 用户-视频互动表tb_user_video_log iduidvideo_idstart_timeend_timeif_followif_likeif_retweetcomment_id110120012021-09-01 10:00:002021-09-01 10:00:20011NULL210520022021-09-10 11:00:002021-09-10 11:00:30101NULL310120012021-10-01 10:00:002021-10-01 10:00…...
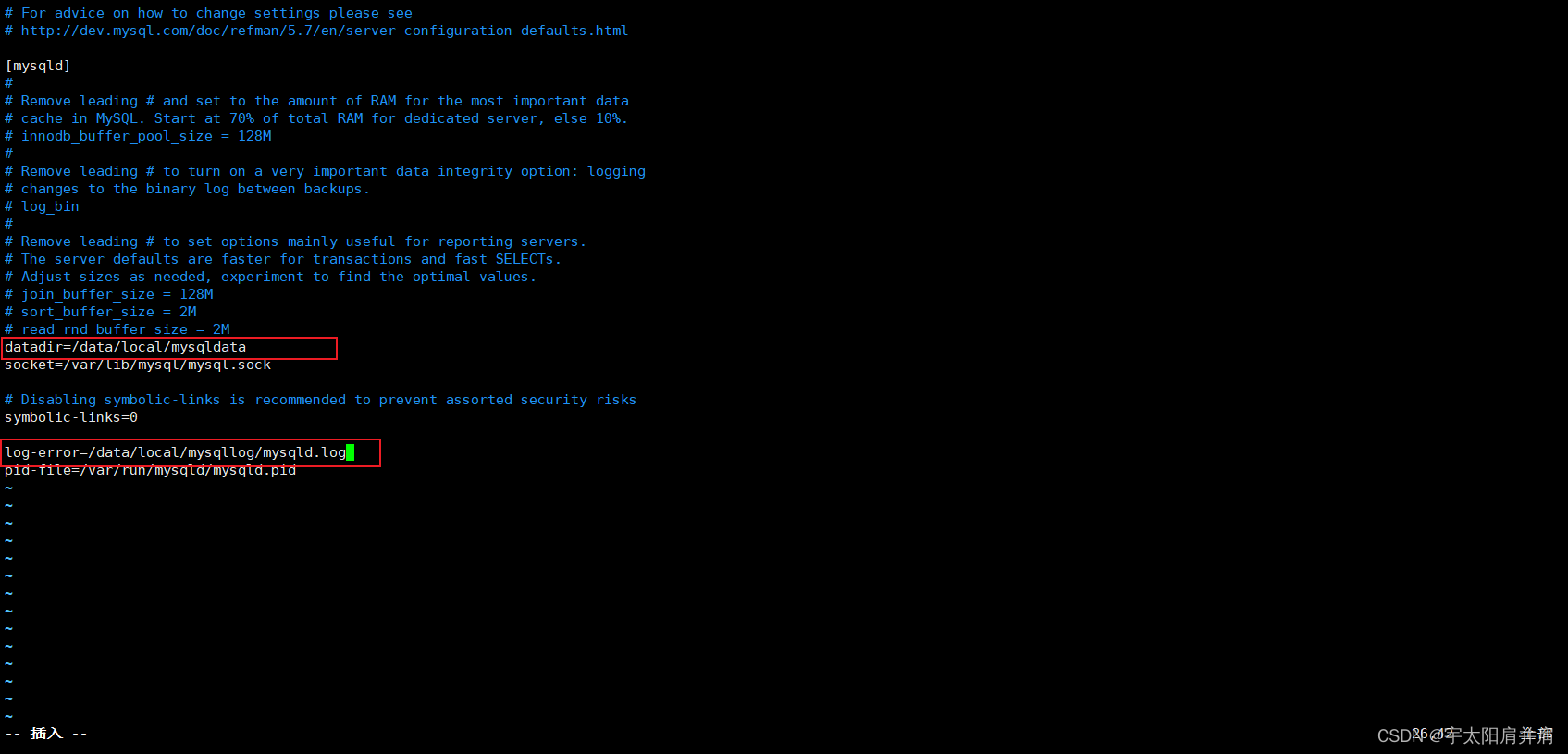
Linux安装MySQL教程【带图文命令巨详细】
巨详细Linux安装MySQL 1、查看是否有自带数据库或残留数据库信息1.1检查残留mysql1.2检查并删除残留mysql依赖1.3检查是否自带mariadb库 2、下载所需MySQL版本,上传至系统指定位置2.1创建目录2.2下载MySQL压缩包 3、安装MySQL3.1创建目录3.2解压mysql压缩包3.3安装解…...
外部排序快速入门详解:基本原理,败者树,置换-选择排序,最佳归并树
文章目录 外部排序1.最基本的外部排序原理2.外部排序的优化2.1 败者树优化方法2.2 置换-选择排序优化方法2.3 最佳归并树 外部排序 为什么要学习外部排序? 答: 在处理数据的过程中,我们需要把磁盘(外存)中存储的数据拿到内存中处理…...

人工智能和物联网如何结合
欢迎来到 Papicatch的博客 目录 🍉引言 🍉AI与IoT的结合方式 🍈数据处理和分析 🍍实例 🍈边缘计算 🍍实例 🍈自动化和自主操作 🍍实例 🍈安全和隐私保护 &…...

【JAVASE】JAVA应用案例(下)
一:抢红包 一个大V直播时,发起了抢红包活动,分别有9,666,188,520,99999五个红包。请模拟粉丝来抽奖,按照先来先得,随机抽取,抽完即止,注意:一个红包只能被抽一次,先抽或…...

【面试干货】 B 树与 B+ 树的区别
【面试干货】 B 树与 B 树的区别 1、B 树2、 B 树3、 区别与优缺点比较4、 总结 💖The Begin💖点点关注,收藏不迷路💖 在数据库系统中,B 树和 B 树是常见的索引结构,它们在存储和组织数据方面有着不同的设计…...

Socket编程权威指南(四)彻底解密 Epoll 原理
在上一篇文章中,我们优化了基于 Socket 的网络服务器,从最初的 select/poll 模型进化到了高效的 epoll。很多读者对 epoll 的惊人性能表示极大的兴趣,对它的工作原理也充满了好奇。今天,就让我们一起揭开 epoll 神秘的面纱&#x…...
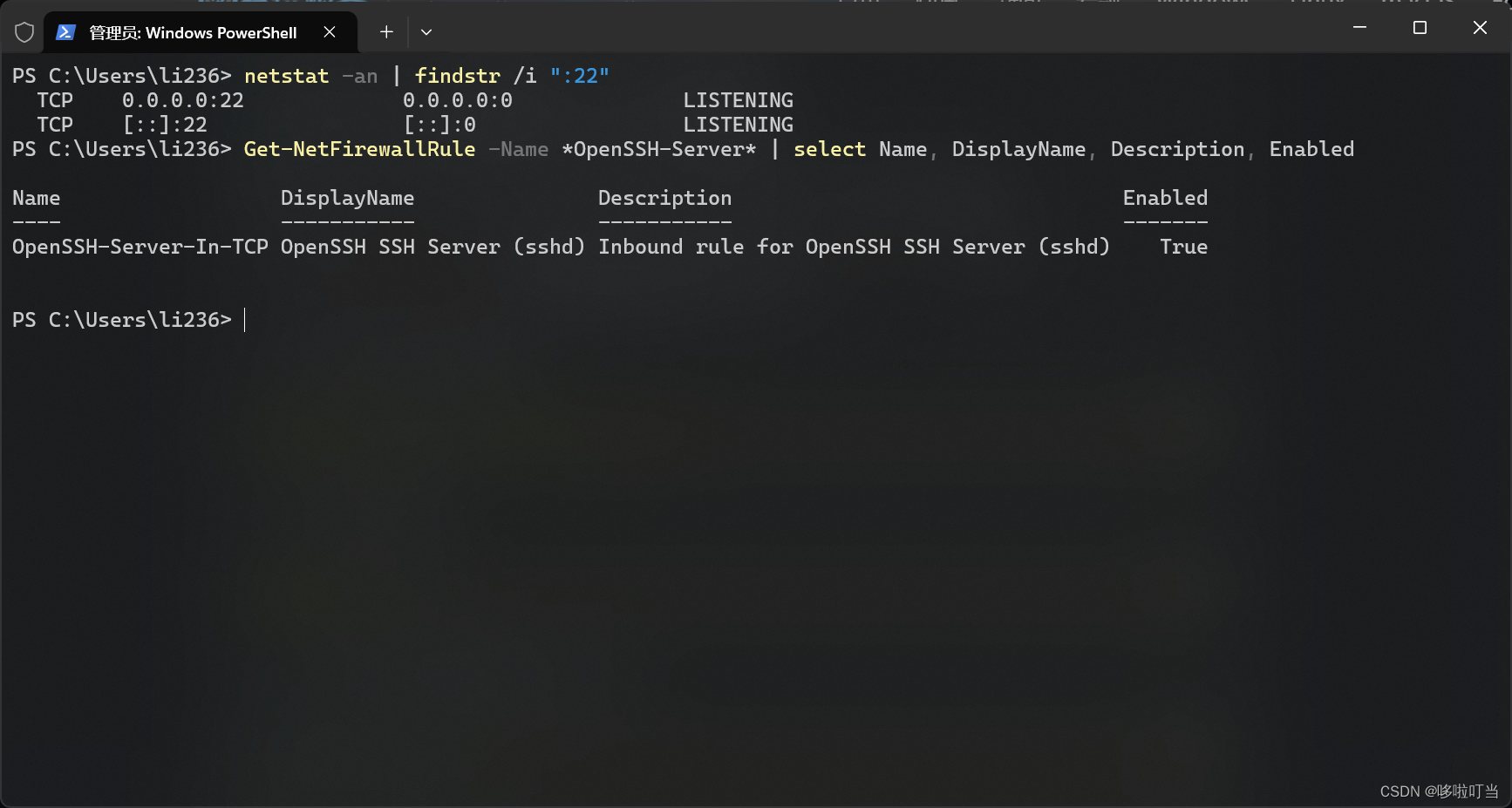
Windows开始ssh服务+密钥登录+默认启用powershell
文章内所有的命令都在power shell内执行,使用右键单击Windows徽标,选择终端管理员即可打开 Windows下OpenSSH的安装 打开Windows power shell,检查SSH服务的安装状态。会返回SSH客户端和服务器的安装状态,一下是两个都安装成功的…...

实体商铺私域流量打造策略:从引流到转化的全链路解析
在数字化时代,实体商铺面临着前所未有的挑战与机遇。随着线上购物的兴起,传统商铺如何吸引并留住顾客,成为了每个实体店家必须面对的问题。私域流量的打造,正是解决这一问题的关键所在。本文将从引流、留存、转化三个方面…...

实战 | 通过微调SegFormer改进车道检测效果(数据集 + 源码)
背景介绍 SegFormer:实例分割在自动驾驶汽车技术的快速发展中发挥了关键作用。对于任何在道路上行驶的车辆来说,车道检测都是必不可少的。车道是道路上的标记,有助于区分道路上可行驶区域和不可行驶区域。车道检测算法有很多种,每…...
翻译《The Old New Thing》- Why do messages posted by PostThreadMessage disappear?
Why do messages posted by PostThreadMessage disappear? - The Old New Thing (microsoft.com)https://devblogs.microsoft.com/oldnewthing/20090930-00/?p16553 Raymond Chen 2008年09月30日 为什么 PostThreadMessage 发布的信息会消失? 在显示用户界面的线…...

【深度学习】—— 神经网络介绍
神经网络介绍 本系列主要是吴恩达深度学习系列视频的笔记,传送门:https://www.coursera.org/deeplearning-ai 目录 神经网络介绍神经网络的应用深度学习兴起的原因 神经网络,全称人工神经网络(Artificial Neural Network…...

python-数字黑洞
[题目描述] 给定一个三位数,要求各位不能相同。例如,352是符合要求的,112是不符合要求的。将这个三位数的三个数字重新排列,得到的最大的数,减去得到的最小的数,形成一个新的三位数。对这个新的三位数可以重…...

SpringCloud 负载均衡 spring-cloud-starter-loadbalancer
简述 spring-cloud-starter-loadbalancer 是 Spring Cloud 中的一个组件,它提供了客户端负载均衡的功能。在 Spring Cloud 的早期版本中,Netflix Ribbon 被广泛用作客户端负载均衡器,但随着时间推移和 Netflix Ribbon 进入维护模式ÿ…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

MFC 抛体运动模拟:常见问题解决与界面美化
在 MFC 中开发抛体运动模拟程序时,我们常遇到 轨迹残留、无效刷新、视觉单调、物理逻辑瑕疵 等问题。本文将针对这些痛点,详细解析原因并提供解决方案,同时兼顾界面美化,让模拟效果更专业、更高效。 问题一:历史轨迹与小球残影残留 现象 小球运动后,历史位置的 “残影”…...

windows系统MySQL安装文档
概览:本文讨论了MySQL的安装、使用过程中涉及的解压、配置、初始化、注册服务、启动、修改密码、登录、退出以及卸载等相关内容,为学习者提供全面的操作指导。关键要点包括: 解压 :下载完成后解压压缩包,得到MySQL 8.…...
