归并排序——逆序数对的统计
逆序数对的统计
题目描述

运行代码
#include <iostream>
using namespace std;
#define LL long long
const int N = 1e5 + 5;
int a[N], tmp[N];
LL merge_sort(int q[], int l, int r)
{if (l >= r)return 0; int mid = l + r >> 1; LL res = merge_sort(q, l, mid) + merge_sort(q, mid + 1, r); int k = 0, i = l, j = mid + 1;while (i <= mid && j <= r)if (q[i] <= q[j]) tmp[k ++ ] = q[i ++ ];else{res += mid - i + 1;tmp[k ++ ] = q[j ++ ];}while (i <= mid)tmp[k ++ ] = q[i ++ ];while (j <= r)tmp[k ++ ] = q[j ++ ];for (i = l, j = 0; i <= r; i ++, j ++ )q[i] = tmp[j]; return res;
}
int main()
{int n;scanf("%d", &n);for (int i = 0; i < n; i ++ )
scanf("%d", &a[i]); cout << merge_sort(a, 0, n - 1) << endl; return 0;
}
代码思路
宏定义与常量
#define LL long long:定义LL为long long类型的别名,用于存储较大的整数,例如逆序对的数量。const int N = 1e5 + 5;:定义数组的最大容量,适用于最多100,005个元素的数组。
函数merge_sort此函数递归地将数组分成更小的部分,然后合并这些部分,同时计算逆序对总数。
- 参数:
q[]是要排序的数组,l和r分别是当前子数组的左右边界(索引)。 - 基础情况:当左边界大于等于右边界时(即子数组只有一个或没有元素),返回0,表示该子数组没有逆序对。
- 分解:计算中间索引
mid,递归地对左右两部分[l, mid]和[mid+1, r]进行排序并计算逆序对,将结果累加到res中。 - 合并:
- 初始化辅助数组
tmp和三个指针k, i, j。当i未超过mid且j未超过r时,比较q[i]和q[j]的大小:- 如果
q[i] <= q[j],说明当前元素不会形成新的逆序对,将q[i]放入tmp,并移动i和k。 - 否则,所有
q[i]到q[mid]之间的元素都比q[j]大,因此增加了mid - i + 1个逆序对,将q[j]放入tmp,移动j和k。
- 如果
- 分别处理剩余的元素,将它们依次放入
tmp。将tmp中的元素复制回原数组q。
- 初始化辅助数组
- 返回值:最终返回整个数组排序过程中的逆序对总数
res。 - 主函数
main:读取数组长度n。通过循环读取数组a中的每个元素。调用merge_sort函数,传入数组a和其边界(0和n-1),输出计算得到的逆序对总数。
改进思路
- 使用指针直接操作数组:在
mergeSortAndCount函数中,直接使用指针i,j,k而非索引,这在某些情况下可以略微提高访问效率。 - 保持数组作为参数:继续使用原生数组作为函数参数,保持与原始代码结构的一致性。
- 代码格式和可读性:调整代码格式,确保良好的可读性和一致性,比如增加必要的空格和换行。
- 去除不必要的类型别名:保留
int64_t作为长整型的别名,因为它清晰地表达了数据类型的目的。
改进代码
#include <iostream>
using namespace std;
typedef long long int64_t;
// 使用指针代替数组索引来优化访问速度
int64_t mergeSortAndCount(int a[], int temp[], int left, int right) {if (left >= right) return 0; int mid = left + (right - left) / 2; // 递归排序并计数int64_t inv_count = mergeSortAndCount(a, temp, left, mid);inv_count += mergeSortAndCount(a, temp, mid + 1, right); // 合并阶段计算逆序对int i = left, j = mid + 1, k = left;while (i <= mid && j <= right) {if (a[i] <= a[j]) {temp[k++] = a[i++];} else {inv_count += mid - i + 1;temp[k++] = a[j++];}} // 复制剩余元素while (i <= mid) temp[k++] = a[i++];while (j <= right) temp[k++] = a[j++]; // 将排序结果复制回原数组for (int p = left; p <= right; ++p) a[p] = temp[p]; return inv_count;
}
int main() {const int N = 1e5 + 10;int a[N], temp[N];int n;scanf("%d", &n); for (int i = 0; i < n; ++i) scanf("%d", &a[i]); int64_t inv_count = mergeSortAndCount(a, temp, 0, n - 1);cout << inv_count << endl; return 0;
}其他方法(使用向量) AI生成
#include <iostream>
#include <vector>using namespace std;
using int64_t = long long;// 合并排序并计数逆序对
int64_t mergeSortAndCount(vector<int>& array, vector<int>& temp, int left, int right) {if (left >= right) return 0;int mid = left + (right - left) / 2;// 递归排序左右两边,并计算逆序对int64_t inv_count = mergeSortAndCount(array, temp, left, mid);inv_count += mergeSortAndCount(array, temp, mid + 1, right);// 合并阶段计算逆序对int i = left, j = mid + 1, k = 0;while (i <= mid && j <= right) {if (array[i] <= array[j]) {temp[k++] = array[i++];} else {inv_count += mid - i + 1; // 计算逆序对temp[k++] = array[j++];}}// 处理剩余元素while (i <= mid) temp[k++] = array[i++];while (j <= right) temp[k++] = array[j++];// 将排序结果复制回原数组copy(temp.begin(), temp.begin() + k, array.begin() + left);return inv_count;
}int main() {int n;cin >> n;vector<int> a(n);for (int& elem : a) cin >> elem;vector<int> temp(n); // 临时数组用于合并cout << mergeSortAndCount(a, temp, 0, n - 1) << endl;return 0;
}- 添加函数注释:解释每个函数的作用,特别是
merge_sort中的逻辑。 - 使用更明确的变量名:如将
q[]改为array[],使代码意图更清晰。 - 去除全局变量:尽量减少全局变量的使用,改用函数参数传递。
- 优化类型别名的可读性:将
LL改为更明确的别名,如typedef long long int64_t; - 使用C++风格的输入输出:完全替换
scanf和printf为cin和cout。
归并、插入和冒泡排序比较
归并排序:
- 优点:时间复杂度在平均和最坏情况下都为 ,性能比较稳定,适合大规模数据排序。
- 缺点:需要额外的空间用于合并。
插入排序:
- 优点:对于接近有序的数据表现非常好,在小规模数据或部分有序数据上效率可能较高,代码简单。
- 缺点:最坏情况时间复杂度为 。
冒泡排序:
- 优点:实现简单。
- 缺点:时间复杂度较差,也是 。
一般来说,在数据规模较大且对性能要求较高时,归并排序通常表现更好。但如果数据规模较小或者数据有一定的特殊性(如接近有序),插入排序可能更合适。而冒泡排序相对来说在大多数情况下效率较低,较少被优先选用。
使用归并排序解决逆序数对统计问题思路:
在归并排序的合并过程中,当我们比较左右两部分元素时,左边部分一个较大元素如果出现在右边部分较小元素之前,那么就构成一个逆序数对。
当左边当前元素大于右边当前元素时,由于左右两边都是已排序的,那么左边该元素之后的所有元素与右边当前元素都构成逆序数对,数量为左边当前未处理元素的数量。我们可以在合并的同时统计这样的逆序数对数量。通过递归地执行归并排序,不断在合并过程中累加逆序数对的数量,最终就能得到总的逆序数对数量。
例如,假设有数组 [3, 1, 4, 2],在第一次合并 [3] 和 [1] 时,因为 3 大于 1,此时就找到一个逆序数对,然后继续递归合并其他部分并统计。
相关文章:

归并排序——逆序数对的统计
逆序数对的统计 题目描述 运行代码 #include <iostream> using namespace std; #define LL long long const int N 1e5 5; int a[N], tmp[N]; LL merge_sort(int q[], int l, int r) {if (l > r)return 0; int mid l r >> 1; LL res merge_sort(q, l,…...
)
基于截图和模拟点击的自动化压测工具开发(MFC)
1.背景 想对一个MFC程序做自动压测功能,根据判断程序界面某块区域是否达到预定状态,来自动执行鼠标点击或者键盘输入的操作,以解决测试人员需要重复手动压测问题。 1.涉及的技术 串口控制,基于MFC橡皮筋类(CRectTracker)做一个…...

力扣每日一题 6/10
881.救生艇[中等] 题目: 给定数组 people 。people[i]表示第 i 个人的体重 ,船的数量不限,每艘船可以承载的最大重量为 limit。 每艘船最多可同时载两人,但条件是这些人的重量之和最多为 limit。 返回 承载所有人所需的最小船…...

[知识点] 内存顺序属性的用途和行为
C标准库中定义了以下几种内存顺序属性: std::memory_order_relaxedstd::memory_order_consumestd::memory_order_acquirestd::memory_order_releasestd::memory_order_acq_relstd::memory_order_seq_cst 1. std::memory_order_relaxed 定义:不提供同步…...
索引的创建和优化)
JAVA Mongodb 深入学习(二)索引的创建和优化
一、常用索引类型 1、单个索引 单个索引的创建 db.你的表名.createIndex({"你的字段名":1}) 单个索引的创建且是唯一索引 db.你的表名.createIndex({"你的字段名":1}),{ unique: true }) 2、复合索引 将多个过滤的字段,做成索引,…...

转让北京劳务分包地基基础施工资质条件和流程
地基基础资质转让流程是怎样的?对于企业来说,资质证书不仅是实力的证明,更是获得工程承包的前提。而在有了资质证书后,企业才可以安心的准备工程投标,进而在工程竣工后获得收益。而对于从事地基基础工程施工的企业,需…...
Python基础——字符串
一、Python的字符串简介 Python中的字符串是一种计算机程序中常用的数据类型【可将字符串看作是一个由字母、数字、符号组成的序列容器】,字符串可以用来表示文本数据。 通常使用一对英文的单引号()或者双引号(")…...

AP的数据库性能到底重要吗?
先说结论:没那么重要。甚至可能不重要。 我用我的经历和分析给大家说说。诸位看看如何。 不重要的观点是不是不能接受? 因为这些是站在我们角度觉得的。而实际上使用者(业务或者用户),真的不太在乎我们所在乎的。 …...
Vue3【二】 VSCode需要安装的Vue语法插件
VSCode需要安装的 适配Vue3的插件 Vue-Official插件安装...
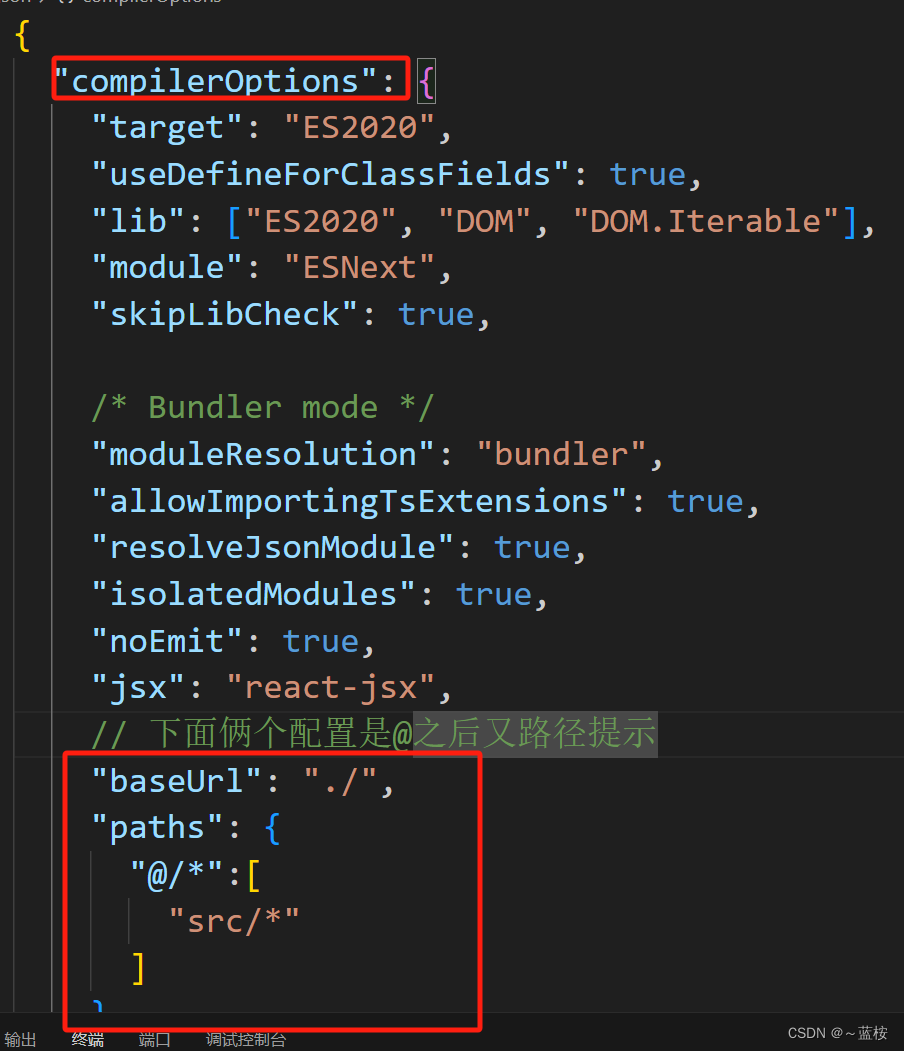
设置路径别名
一、描述 如果想要给路径设置为别名,就是常见的有些项目前面的引入文件通过开头的,也就是替换了一些固定的文件路径,怎么配置。 二、配置 import { defineConfig } from vite import react from vitejs/plugin-react import path from path…...

人事信息管理系统(Java+MySQL)
一、项目背景 在现代企业中,管理大量员工的工作信息、薪资、请假、离职等事务是一项非常繁琐和复杂的任务。传统的手工管理方式不仅效率低下,而且容易出错。为了提高人事管理的效率,减少人工操作带来的错误,企业迫切需要一个高效…...

Python 中生成器与普通函数的区别
在Python中,生成器和普通函数有一些区别。 生成器使用 yield 语句从函数中返回一个值,而不是使用 return 语句。当生成器函数被调用时,它会返回一个迭代器对象,而非立即执行函数体内的代码。 生成器函数可以通过多次调用 yield 语…...
最小栈、栈的弹出(C++)
1.最小栈 思路分析: 代码: class MinStack { public:MinStack() {}void push(int val) {st.push(val);//两种情况需要更新最小值//1.最小栈为空(就是存最小值的那个栈)//2.插入的值小于或等于最小栈的栈顶元素if(minstack.empty()||minstack.top()>…...
20240607每日通信--------VUE3前端引入scoket-io,后端引入Netty-SocketIO,我成功了,希望一起交流沟通
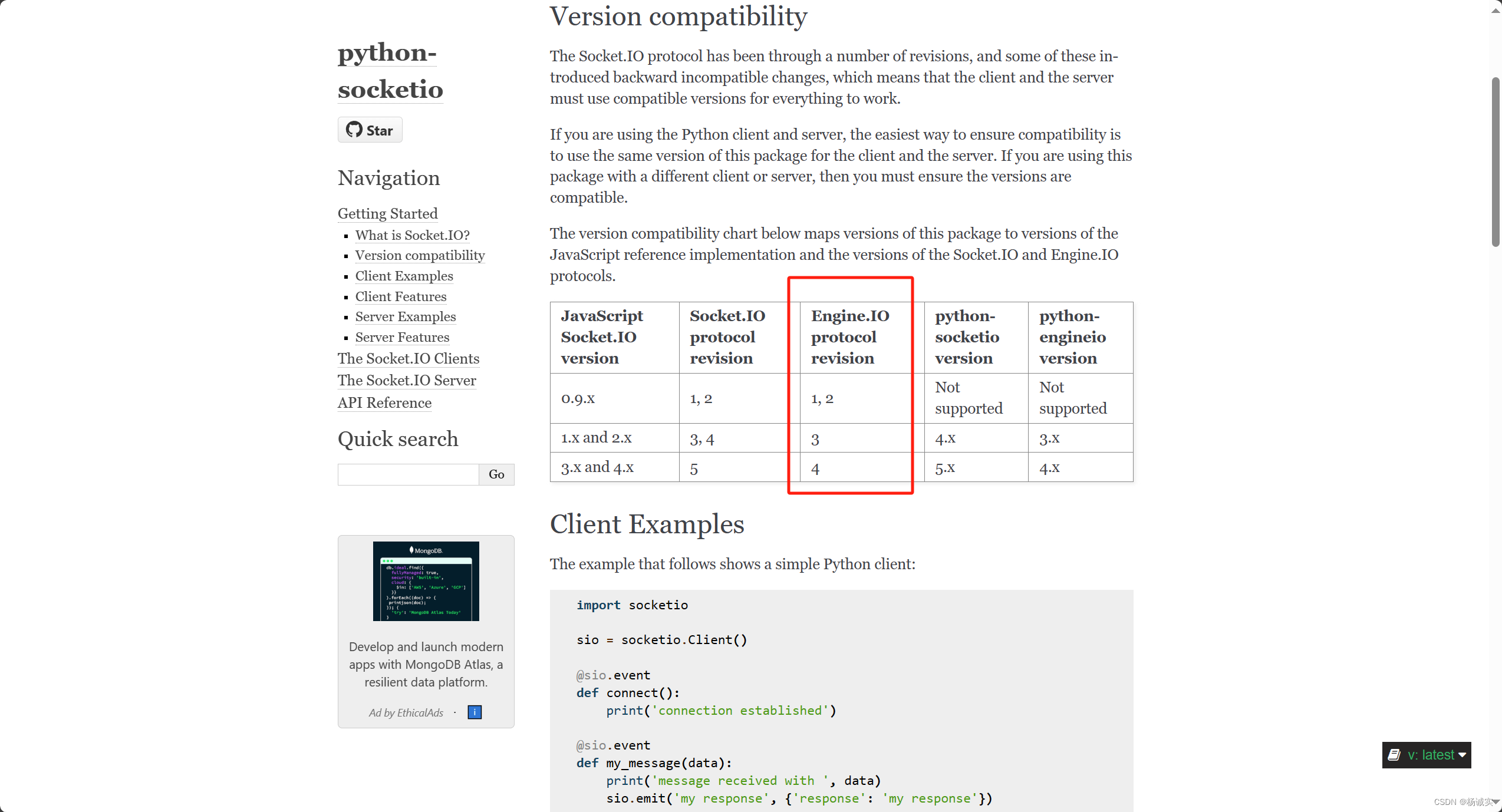
无语 前置: VUE3 前端集成scoket-io socket.io-client Sringboot 3.0JDK17集成Netty-SocketIO Netty-SocketIO 失败原因一: 前期决定要写demo时候,单独了解了,后端引入Netty-SocketIO注意事项,详见我先头写的博客 前…...
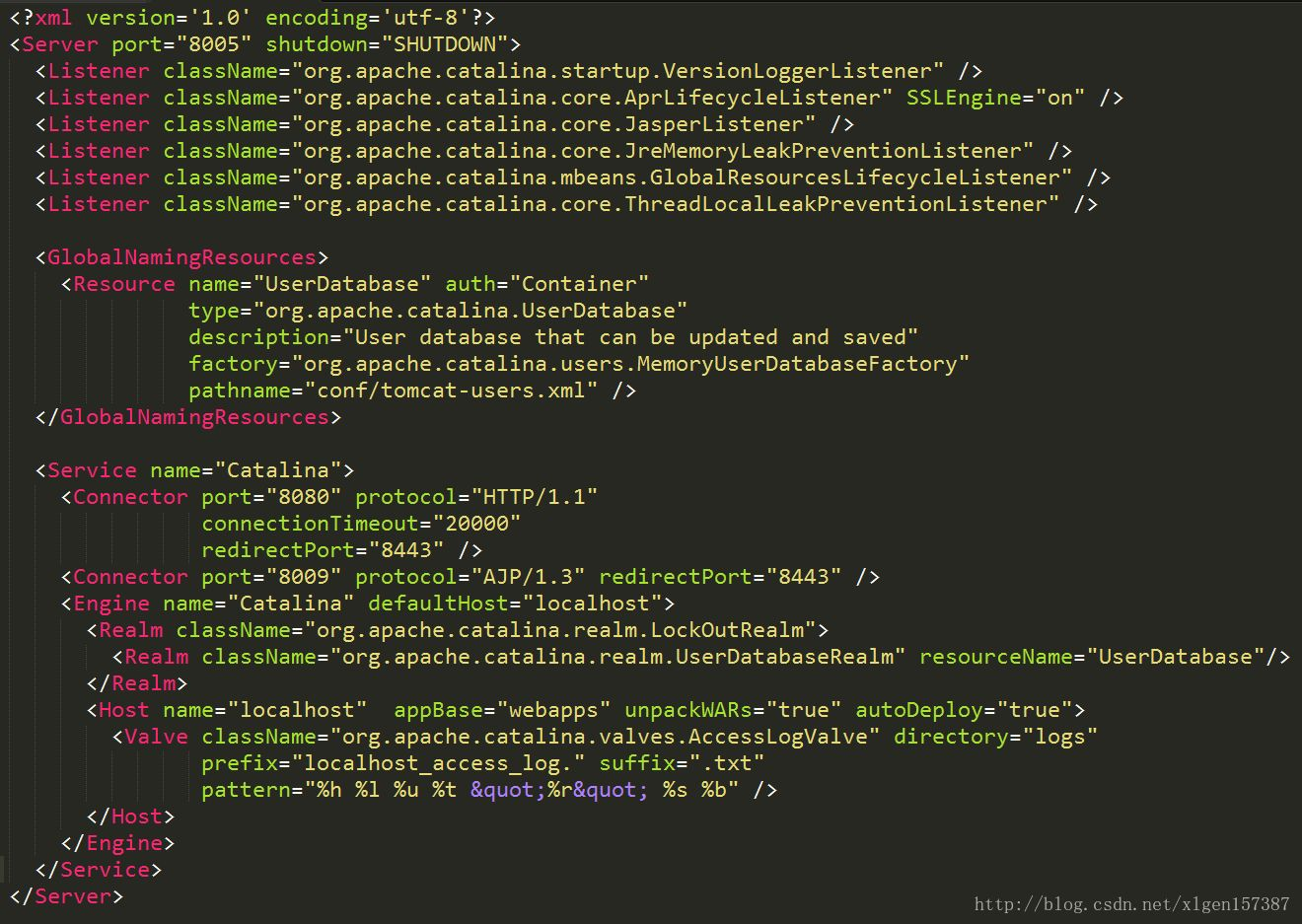
Tomcat源码解析(八):一个请求的执行流程(附Tomcat整体总结)
Tomcat源码系列文章 Tomcat源码解析(一):Tomcat整体架构 Tomcat源码解析(二):Bootstrap和Catalina Tomcat源码解析(三):LifeCycle生命周期管理 Tomcat源码解析(四):StandardServer和StandardService Tomcat源码解析(五)&…...

python使用gdb进行堆栈查看与调试
以ubuntu示例,先安装gdb与python-dbg,dbg按照python版本安装 apt install -y gdb python3.10-dbg 使用top查看python进程,使用gdb操作python进程 gdb python3 6618 加载环境 source /usr/share/gdb/auto-load/usr/bin/python3.10-gdb.py…...

【DevOps】路由与路由器详细介绍:原理、功能、类型及应用场景
目录 一、路由详细介绍 1、什么是路由? 2、路由的基本原理 3、 路由协议 静态路由 动态路由 4、 路由表 5、 路由算法 6、路由的优缺点 优点 缺点 7、 路由应用场景 二、路由器详细介绍 1、什么是路由器? 2、 路由器的工作原理 3、路由器…...

【WP|9】深入解析WordPress [add_shortcode]函数
add_shortcode 是 WordPress 中一个非常强大的函数,用于创建自定义的短代码(shortcodes)。短代码是一种简洁的方式,允许用户在内容中插入动态的、可重用的功能。通过 add_shortcode,开发者可以定义自己的短代码&#x…...

Qt QStackedWidget类详细分析
一.定义 QStackedWidget类是一个容器控件,它提供了一个堆叠的页面布局方式,每个页面可以包含一个子部件。在QStackedWidget中,只有当前活动的页面是可见的,其他页面会被隐藏起来。 QStackedWidget类的常用方法包括: a…...
)
Java数据结构与算法(leetcode热题881. 救生艇)
前言 救生艇属于贪心算法,解题之前条件一定要归纳好。题目中存在3个要求: 1.一艘船最多坐2人 2.船数要求最小 3.每艘船重量小于limit 意味着体重较轻的两人可以同乘一艘救生艇。 . - 力扣(LeetCode) 实现原理 1.重量大的有…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...

【Redis】笔记|第8节|大厂高并发缓存架构实战与优化
缓存架构 代码结构 代码详情 功能点: 多级缓存,先查本地缓存,再查Redis,最后才查数据库热点数据重建逻辑使用分布式锁,二次查询更新缓存采用读写锁提升性能采用Redis的发布订阅机制通知所有实例更新本地缓存适用读多…...
