贪心算法06(leetcode738,968)
参考资料:
https://programmercarl.com/0738.%E5%8D%95%E8%B0%83%E9%80%92%E5%A2%9E%E7%9A%84%E6%95%B0%E5%AD%97.html
738. 单调递增的数字
题目描述:
当且仅当每个相邻位数上的数字 x 和 y 满足 x <= y 时,我们称这个整数是单调递增的。
给定一个整数 n ,返回 小于或等于 n 的最大数字,且数字呈 单调递增 。
示例 1:
输入: n = 10 输出: 9
思路分析:
从后往前遍历,若两两不符合递增,则前一位数值-1,并将start(‘9’开始的下标)设为后一位的index
注意:1. start初始为len,考虑到如“1234”的情况
2.转为字符数组便于处理
代码实现:
class Solution {public int monotoneIncreasingDigits(int n) {String s=String.valueOf(n);char[] chars=s.toCharArray();int len=chars.length;int start=len;//9开始的下标for(int i=len-2;i>=0;i--){//后往前if(chars[i]>chars[i+1]){chars[i]--;start=i+1;}}for(int i=start;i<len;i++){chars[i]='9';}return Integer.parseInt(String.valueOf(chars));}
}968. 监控二叉树
题目描述:
给定一个二叉树,我们在树的节点上安装摄像头。
节点上的每个摄影头都可以监视其父对象、自身及其直接子对象。
计算监控树的所有节点所需的最小摄像头数量。
示例 1:

输入:[0,0,null,0,0] 输出:1 解释:如图所示,一台摄像头足以监控所有节点
思路分析:
1. 后序遍历(左右中):每个叶子结点都要被监视到
2. 贪心:叶子节点的父节点放监控,最大范围的监控。
3. 每个节点的三种状态:(0)无覆盖(1)有覆盖,无放监控(2)放监控 。
4. 四种情况:(1)左右孩子都是“1”,则自己是“0”(2)左右孩子之一是“0”,则自己是“2”(3)剩下的情况(任一孩子是“2”),则自己是“1” //(4)本应在root的上一个节点放监控,但root没有上一个,该情况在main()函数中处理。
代码实现:
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {int res;public int minCameraCover(TreeNode root) {res=0;if(f(root)==0) res++;return res;}public int f(TreeNode cur){if(cur==null) return 1;// 0:无覆盖// 1:有覆盖,无监控// 2:有覆盖,有监控// 后序遍历:左右中int l=f(cur.left);//左int r=f(cur.right);//右//中if(l==1 && r==1) return 0;if(l==0 || r==0){res++;return 2;}return 1;}
}相关文章:

贪心算法06(leetcode738,968)
参考资料: https://programmercarl.com/0738.%E5%8D%95%E8%B0%83%E9%80%92%E5%A2%9E%E7%9A%84%E6%95%B0%E5%AD%97.html 738. 单调递增的数字 题目描述: 当且仅当每个相邻位数上的数字 x 和 y 满足 x < y 时,我们称这个整数是单调递增的。…...

cve_2022_0543-redis沙盒漏洞复现 vulfocus
1. 原理 该漏洞的存在是因为Debian/Ubuntu中的Lua库是作为动态库提供的。自动填充了一个package变量,该变量又允许访问任意 Lua 功能。 2.复现 我们可以尝试payload: eval local io_l package.loadlib("/usr/lib/x86_64-linux-gnu/liblua5.1.so…...
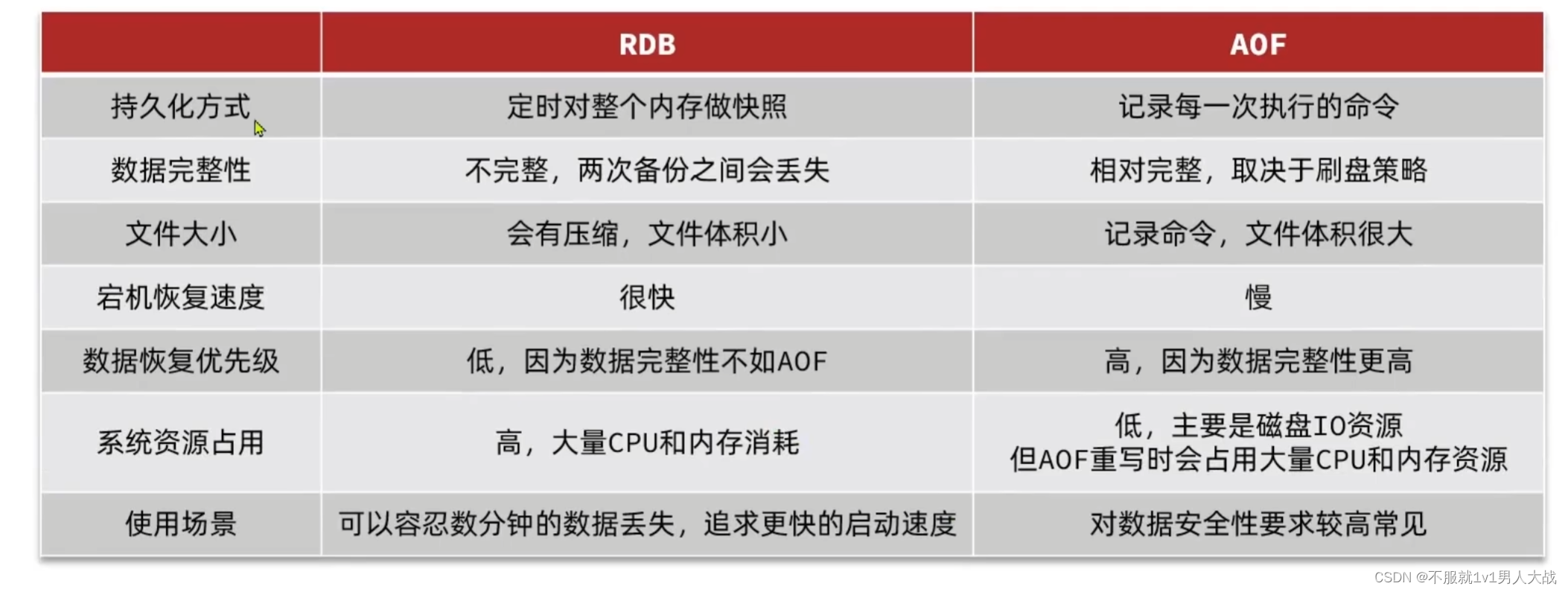
浅解Reids持久化
Reids持久化 RDB redis的存储方式: rdb文件都是二进制,很小,里面存的是数据 实现方式 redis-cli链接到redis服务端 使用save命令 注:不推荐 因为save命令是直接写到磁盘里面,速度特别慢,一般都是redis…...
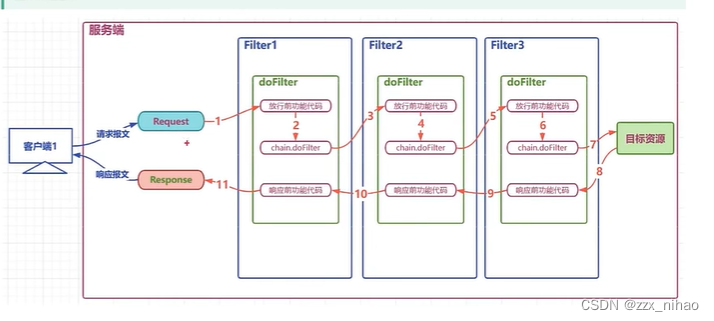
Java24:会话管理 过滤器 监听器
一 会话管理 1.cookie 是一种客户端会话技术,cookie由服务端产生,它是服务器存放在浏览器的一小份数据,浏览器 以后每次访问服务器的时候都会将这小份的数据带到服务器去。 //创建cookie对象 Cookie cookie1new Cookie("…...

web前端电影简介标签:深度解析与创意应用
web前端电影简介标签:深度解析与创意应用 在web前端开发中,电影简介标签的设计与实现是一项既具挑战性又充满创意的任务。这些标签不仅需要准确传达电影的核心信息,还要通过精美的设计和交互效果吸引用户的眼球。本文将从四个方面、五个方面…...

Java面向对象-方法的重写、super
Java面向对象-方法的重写、super 一、方法的重写二、super关键字1、super可以省略2、super不可以省略3、super修饰构造器4、继承条件下构造方法的执行过程 一、方法的重写 1、发生在子类和父类中,当子类对父类提供的方法不满意的时候,要对父类的方法进行…...

解锁ChatGPT:从GPT-2实践入手解密ChatGPT
⭐️我叫忆_恒心,一名喜欢书写博客的研究生👨🎓。 如果觉得本文能帮到您,麻烦点个赞👍呗! 近期会不断在专栏里进行更新讲解博客~~~ 有什么问题的小伙伴 欢迎留言提问欧,喜欢的小伙伴给个三连支…...
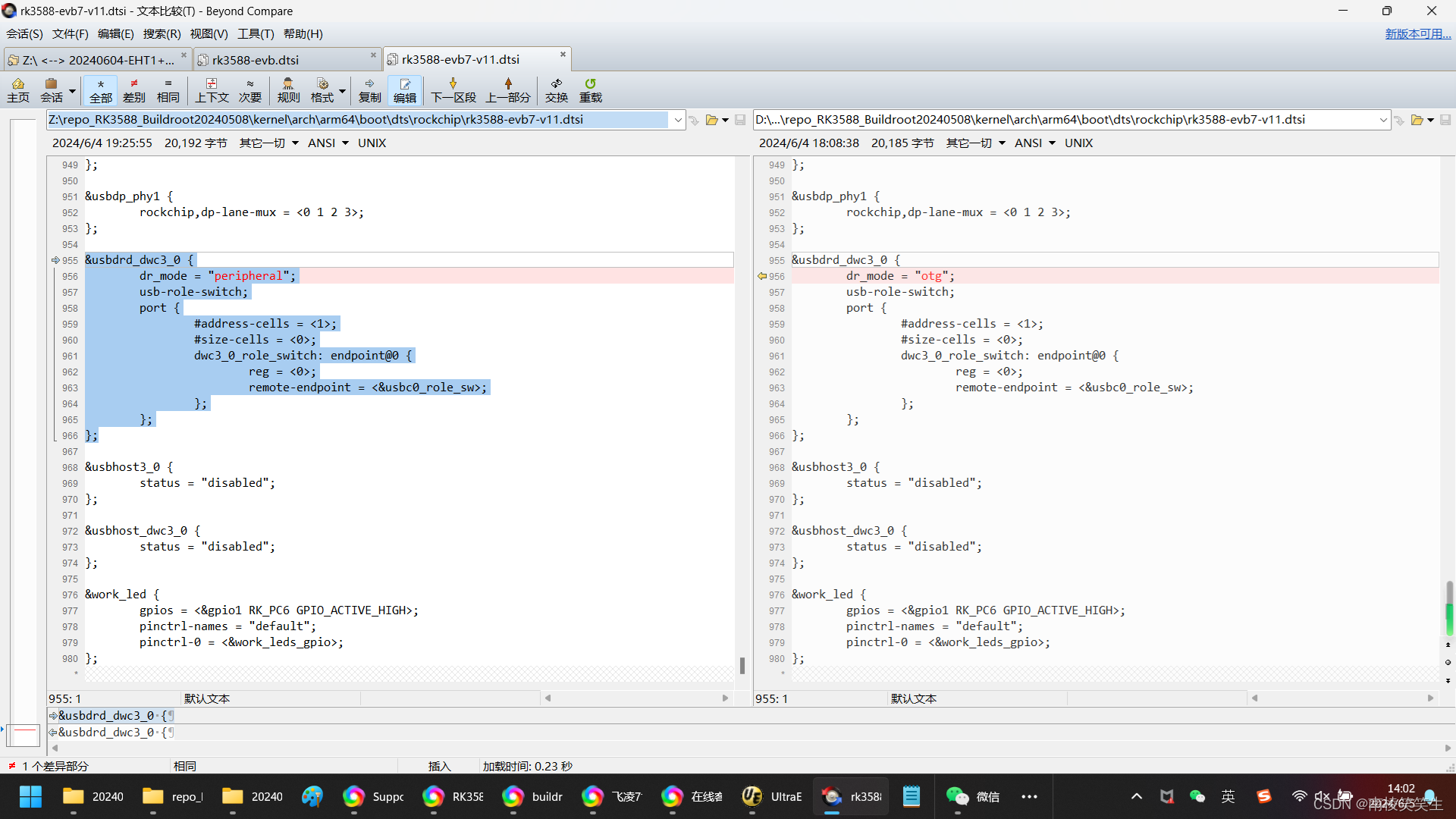
20240605解决飞凌的OK3588-C的核心板刷机原厂buildroot不能连接ADB的问题
20240605解决飞凌的OK3588-C的核心板刷机原厂buildroot不能连接ADB的问题 2024/6/5 13:53 rootrootrootroot-ThinkBook-16-G5-IRH:~/repo_RK3588_Buildroot20240508$ ./build.sh --help rootrootrootroot-ThinkBook-16-G5-IRH:~/repo_RK3588_Buildroot20240508$ ./build.sh lun…...

c++手写的bitset
支持stl bitset 类似的api #include <iostream> #include <vector> #include <climits> #include <utility> #include <stdexcept> #include <iterator>using namespace std;const int W 64;class Bitset { private:vector<unsigned …...
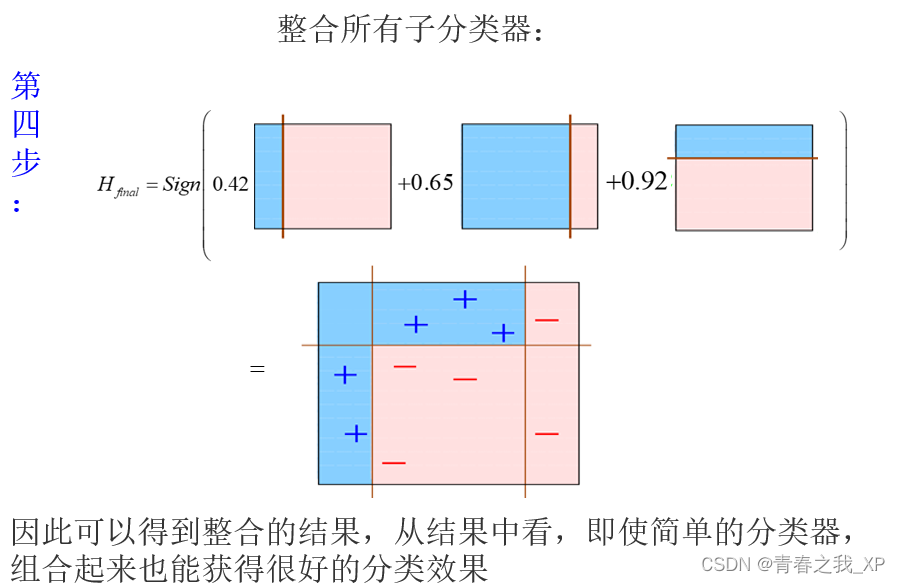
【机器学习系列】深入理解集成学习:从Bagging到Boosting
目录 一、集成方法的一般思想 二、集成方法的基本原理 三、构建集成分类器的方法 常见的有装袋(Bagging)和提升(Boosting)两种方法 方法1 :装袋(Bagging) Bagging原理如下图: …...

用FFMPEG对YUV序列进行编辑的笔记
还是单独开一个吧 每次找挺烦的 播放YUV序列 ffmpeg -f rawvideo -pix_fmt yuv420p -s 3840x2160 -i "Wood.yuv" -vf "scale1280x720" -c:v rawvideo -pix_fmt yuv420p -f sdl "Wood"4K序列转720P ffmpeg -f rawvideo -pix_fmt yuv420p -s 38…...

智能投顾:重塑金融理财市场,引领行业新潮流
一、引言 在数字化浪潮的推动下,金融行业正经历着前所未有的变革。其中,智能投顾作为金融科技的重要分支,以其高效、便捷和个性化的服务,逐渐成为金融理财市场的新宠。本文旨在探讨智能投顾如何引领金融理财新潮流,通过丰富的案例及解决方案,展示其独特的魅力和价值。 二…...

iOS18 新变化提前了解,除了AI还有这些变化
iOS 18即将在不久的将来与广大iPhone用户见面,这次更新被普遍认为是苹果历史上最重要的软件更新之一。据多方报道和泄露的消息,iOS 18将带来一系列全新的功能和改进,包括在人工智能领域的重大突破、全新的设计元素以及增强的性能和安全性。现…...

力扣算法题:多数元素 --多语言实现
无意间看到,力扣存算法代码居然还得升级vip。。。好吧,我自己存吧 golang: func majorityElement(nums []int) int {count : 0condidate : 0for _,val : range nums {if count 0 {condidate valcount 1} else if val condidate {count} …...

[Kubernetes] 容器运行时 Container Runtime
文章目录 1.容器运行时(Container Runtime)2.容器运行时接口3.容器运行时层级4.容器运行时比较5.强隔离容器6.K8S为何难以实现真正的多租户 1.容器运行时(Container Runtime) Container Runtime 是运行于 k8s 集群每个节点中,负责容器的整个生命周期。Docker 就目前…...

10进制与二、八、十六进制的转换
x进制转10进制 1、如八进制数123,通过把每一位数字和8的指数级进行相乘 1 * 8^2 2 * 8^1 3 * 8^01 * 64 2 * 8 3 * 164 16 383 2、十六进制1A3 1 * 16^2 A(即10) * 16^1 3 * 16^01 * 256 10 * 16 3 * 1256 160 3419 3、二进制1010 1 * 2^3 0 * 2…...

日常实习-小米计算机视觉算法岗面经
文章目录 流程问题请你写出项目中用到的模型代码,Resnet50(1)网络退化现象:把网络加深之后,效果反而变差了(2)过拟合现象:训练集表现很棒,测试集很差 把你做的工作里面的…...
string模拟实现)
(C++)string模拟实现
string底层是一个是字符数组 为了跟库里的string区别,所以定义一个命名空间将类string包含 一、构造 1.构造函数 注意:将char*传给const char*是范围缩小,因此只能1:1构造一个 strlen遇到nullptr解引用会报错,因此…...
类和对象的学习总结(一)
面向对象和面向过程编程初步认识 C语言是面向过程的,关注过程(分析求解问题的步骤) 例如:外卖,关注点菜,接单,送单等 C是面向对象的,关注对象,把一件事拆分成不同的对象&…...

力扣22. 括号生成
数字 n 代表生成括号的对数,请你设计一个函数,用于能够生成所有可能的并且有效的括号组合。 示例 1:输入:n 3 输出:["((()))","(()())","(())()","()(())","()()(…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

MySQL JOIN 表过多的优化思路
当 MySQL 查询涉及大量表 JOIN 时,性能会显著下降。以下是优化思路和简易实现方法: 一、核心优化思路 减少 JOIN 数量 数据冗余:添加必要的冗余字段(如订单表直接存储用户名)合并表:将频繁关联的小表合并成…...

【 java 虚拟机知识 第一篇 】
目录 1.内存模型 1.1.JVM内存模型的介绍 1.2.堆和栈的区别 1.3.栈的存储细节 1.4.堆的部分 1.5.程序计数器的作用 1.6.方法区的内容 1.7.字符串池 1.8.引用类型 1.9.内存泄漏与内存溢出 1.10.会出现内存溢出的结构 1.内存模型 1.1.JVM内存模型的介绍 内存模型主要分…...
