【机器学习系列】深入理解集成学习:从Bagging到Boosting
目录
一、集成方法的一般思想
二、集成方法的基本原理
三、构建集成分类器的方法
常见的有装袋(Bagging)和提升(Boosting)两种方法
方法1 :装袋(Bagging)
Bagging原理如下图:
方法2 :提升(Boosting)
Boosting工作原理
目前已有几个Boosting算法,其区别在于:
四、随机森林(Bagging集成方法的一种)
(一)随机森林bagging的思想:
(二)随机森林中的每棵树是怎么生成的呢?
(三) 为什么要随机抽样训练集?
(四)为什么要有放回地抽样?
随机森林Python实现
五、Adaboosting (Boosting集成方法的一种)
(一)基本思想
(二)Adaboosting举例说明
本文将探讨集成学习方法的核心概念,包括其基本原理和两种主流技术:装袋(Bagging)与提升(Boosting)。我们将深入了解随机森林——一种基于Bagging的集成方法,并讨论其背后的思想、树的生成过程以及抽样策略。同时,我们也将介绍Adaboost算法的基本思想和工作原理,并通过实例加以说明。通过这篇文章,读者可以获得对集成分类器构建方法的全面了解,并掌握如何在Python中实现随机森林。
一、集成方法的一般思想
聚集多个分类器的预测来提高分类准确率,这种技术称为组合(ensemble)或分类器组合(classifier combination)方法,也就是集成方法
由训练数据构建一组基分类器,然后通过对每个基分类器的预测进行投票来进行分类。

二、集成方法的基本原理
假定有 25 基分类器:– 每个基分类器的误差均为 e = 0.35– 假定基分类器是独立的– 通过对这些基分类器的预测进行多数表决方法预测类标号– 仅当超过一半的基分类器都预测错误时,组合分类器才会做出错误的预测,此时误差率为: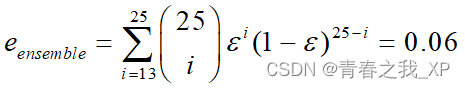 远远低于基分类器的误差率。
远远低于基分类器的误差率。
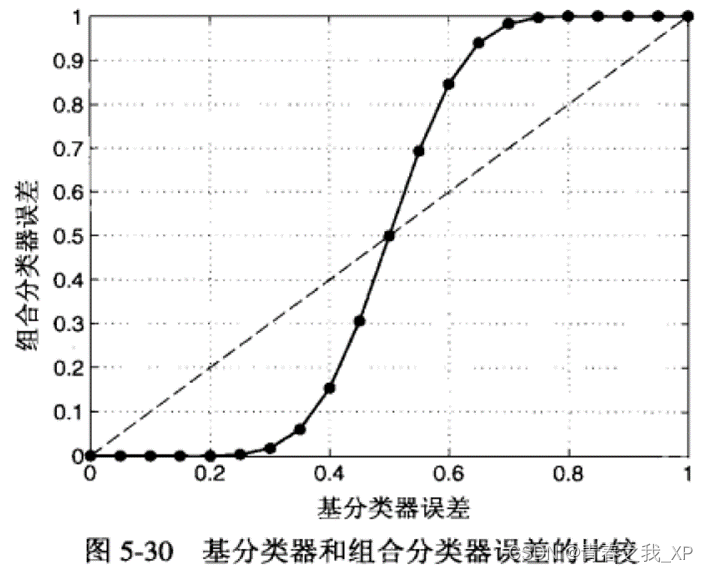
下图显示对于不同的基分类器误差率 e 下的 25 个二元分类器的组合分类器误差率 。对角虚线表示所有基分类器都是等同的情况实线表示所有基分类器独立时的情况e > 0.5 时,组合分类器的性能不如基分类器
三、构建集成分类器的方法
基本思想:
在原始数据上构建多个分类器,然后在分类未知样本时聚集它们的预测结果。
常见的有装袋(Bagging)和提升(Boosting)两种方法
方法1 :装袋(Bagging)
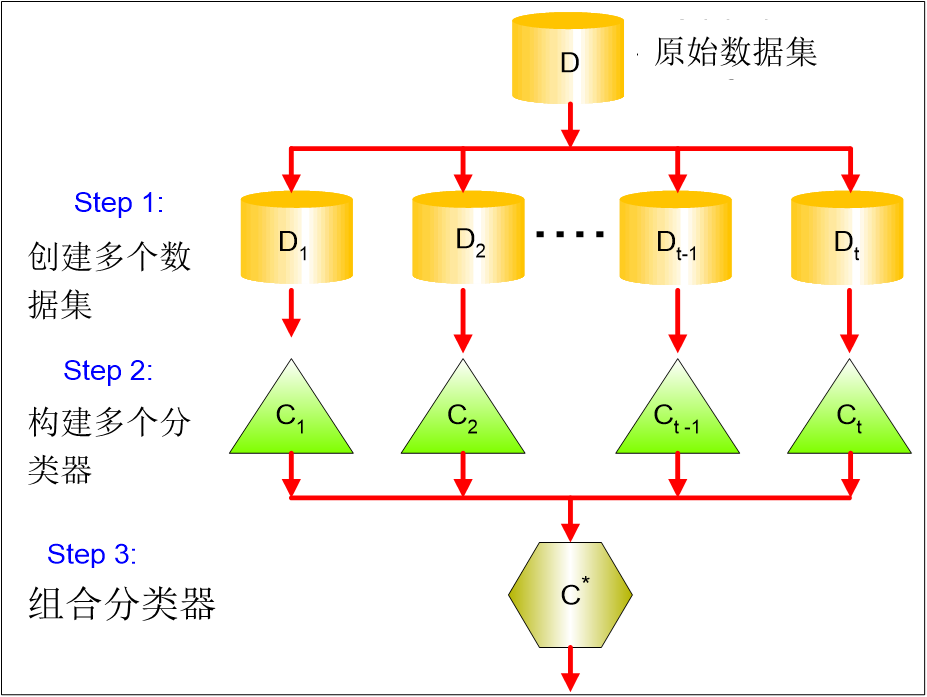
Bagging原理如下图:
对于未知样本Z,预测Z的类标号
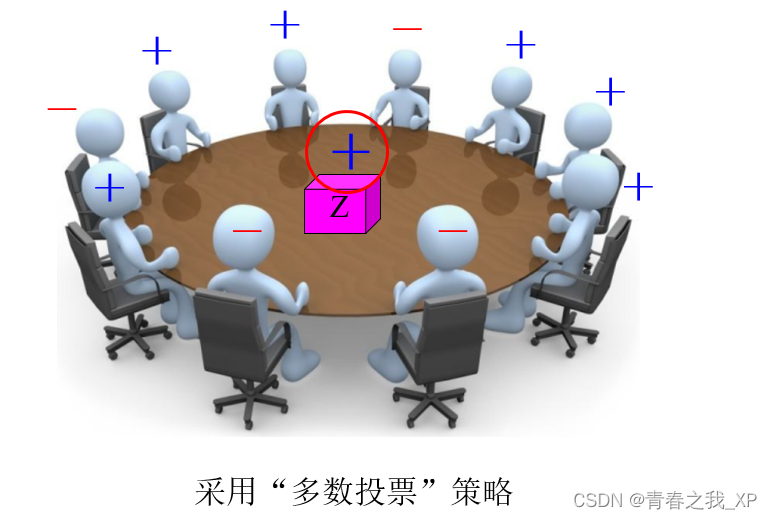
方法2 :提升(Boosting)
Boosting 方法是一种用来提高 弱分类算法 准确度的方法。通过构造一个预测 函数 系列 , 然后以一定的方式将他们组合成一个预测函数。Boosting 是一种提高任意给定学习算法准确度的方法。
Boosting 方法是一种针对提高弱分类算法准确度的有效技术。该方法的核心思想是通过构建一系列的预测函数,并将它们以特定的方式组合起来,从而形成一个更为强大和精准的预测模型。
具体而言,Boosting 通过以下步骤来提升任意给定学习算法的准确度:
初始化:首先选择一个弱分类器作为基础模型,并确定一个权重分配方案,初始时通常所有数据点的权重相等。
迭代训练:在每一轮迭代中,根据上一次迭代中分类错误的样本调整权重,使得错误分类的样本在下一轮迭代中得到更多的关注。然后,使用调整后的权重训练新的弱分类器。
组合预测:将每个弱分类器的预测结果按照一定的权重进行组合,通常是加权投票或加权平均,以形成最终的预测函数。这个组合过程能够有效提升整体模型的准确度。
Boosting 方法的特点在于:
- 逐步增强:通过迭代的方式逐步增强模型的预测能力,每一步都试图修正上一步的错误。
- 权重调整:动态调整样本权重,使得模型在后续的学习过程中更加关注那些难以分类的样本。
- 模型组合:将多个弱分类器智能组合,形成一个强大的分类器,通常比单个分类器具有更高的准确度和鲁棒性。
总之,Boosting 是一种通用且强大的机器学习算法增强技术,它能够显著提升弱分类算法的性能,使其在许多实际问题中达到或接近最优的分类效果。
其核心思想是“ 三个臭皮匠,顶过诸葛亮 ”。
Boosting工作原理
• 首先从训练集用初始权重训练出一个弱学习器 1 ,根据弱学习器 1 的 学习误差率表现 来 更新 训练样本的权重,使得之前弱学习器 1 学习误差率高的训练样本点的权重变高,使得这些误差率高的点在后面的弱学习器 2 中得到更多的重视。• 然后基于调整权重后的训练集来训练弱学习器 2. ,如此重复进行,直到弱学习器数达到事先指定的数目 T 。• 最终将这 T 个弱学习器通过集合策略进行整合,得到最终的强学习器。


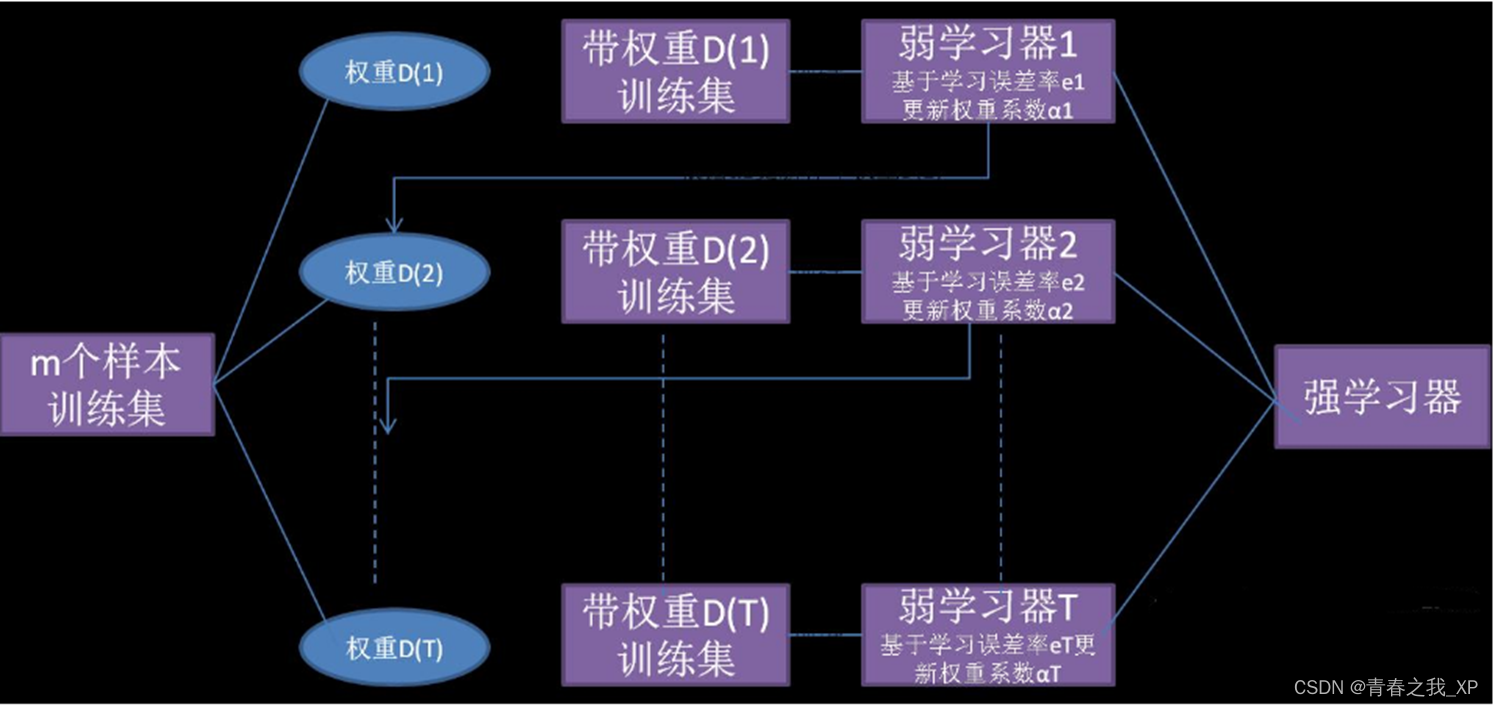
目前已有几个Boosting算法,其区别在于:
(1)每轮Boosting结束时如何更新训练样本的权值;
(2)如何组合每个分类器的预测。
四、随机森林(Bagging集成方法的一种)
随机森林就是通过集成学习的思想将多棵树集成的一种算法,它的基本单元是决策树,而它的本质属于机器学习的一大分支——集成学习方法。
随机森林的名称中有两个关键词,一个是“随机”,一个就是“森林”。
“森林”很好理解,一棵叫做树,那么成百上千棵就可以叫做森林了,其实这也是随机森林的主要思想--集成思想的体现。“随机”的包括随机选取训练样本集和随机选取分裂属性集。
从直观角度来解释,每棵决策树都是一个分类器(假设现在针对的是分类问题),那么对于一个输入样本,N棵树会有N个分类结果。而随机森林集成了所有的分类投票结果,将投票次数最多的类别指定为最终的输出。
(一)随机森林bagging的思想:
将若干个弱分类器的分类结果进行投票选择,从而组成一个强分类器。
(二)随机森林中的每棵树是怎么生成的呢?
一开始提到的随机森林中的“随机”就是指的步骤a和步骤b中的两个随机性。两个随机性的引入对随机森林的分类性能至关重要。由于它们的引入,使得随机森林不容易陷入过拟合,并且具有很好得抗噪能力(比如:对缺省值不敏感) 。
(三) 为什么要随机抽样训练集?
如果不进行随机抽样,每棵树的训练集都一样,那么最终训练出的树分类结果也是完全一样的,这样的话完全没有集成的必要
(四)为什么要有放回地抽样?
如果不是有放回的抽样,那么每棵树的训练样本都是不同的,都是没有交集的,这样每棵树都是“有偏的”或"片面的",也就是说每棵树训练出来都是有很大的差异的;
而随机森林最后分类取决于多棵树(弱分类器)的投票表决,这种表决应该是"求同",因此使用完全不同的训练集来训练每棵树这样对最终分类结果是没有帮助的。
随机森林Python实现
请看下方链接
【机器学习系列】掌握随机森林:从基础原理到参数优化的全面指南_随机森林算法参数解释及调优-CSDN博客
五、Adaboosting (Boosting集成方法的一种)
(一)基本思想

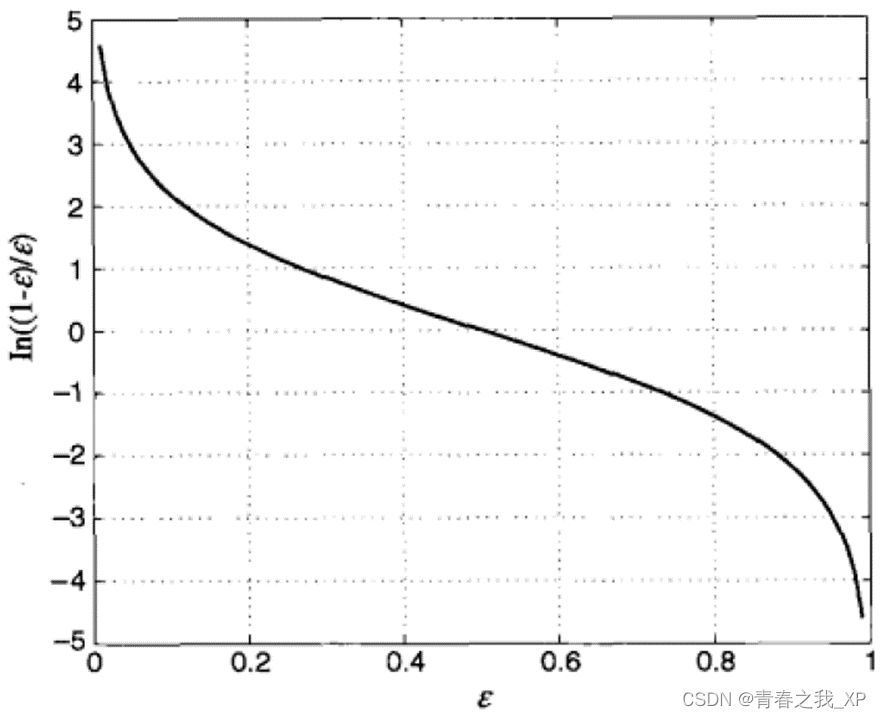
如果错误率ei 接近0,则 αi 有一个很大的正值。
如果错误率ei 接近1,则 αi 有一个很大的负值。

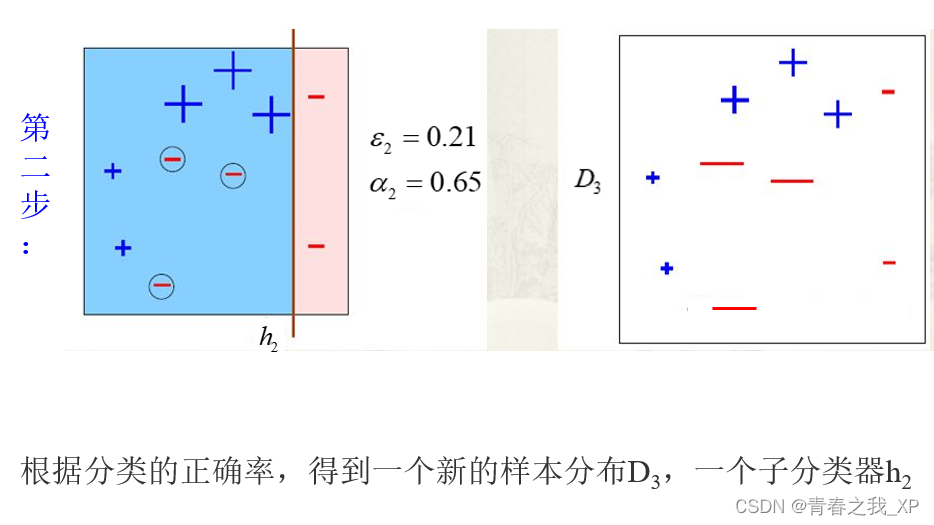
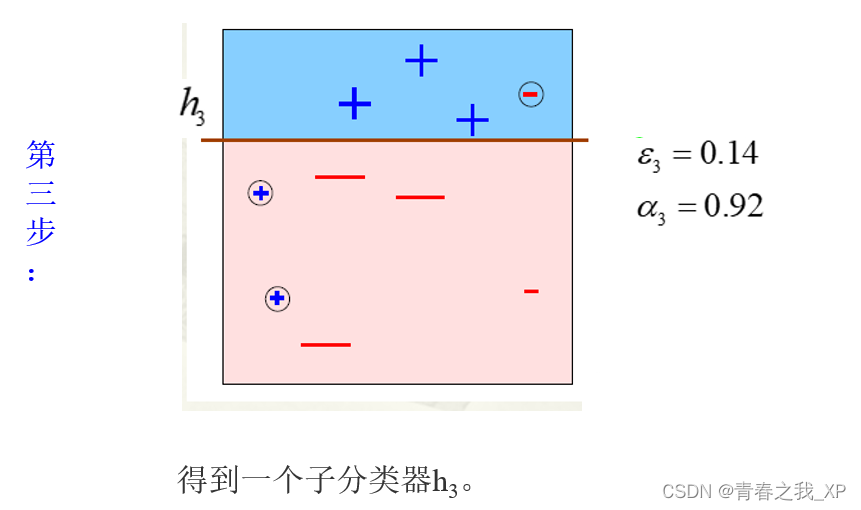
(二)Adaboosting举例说明

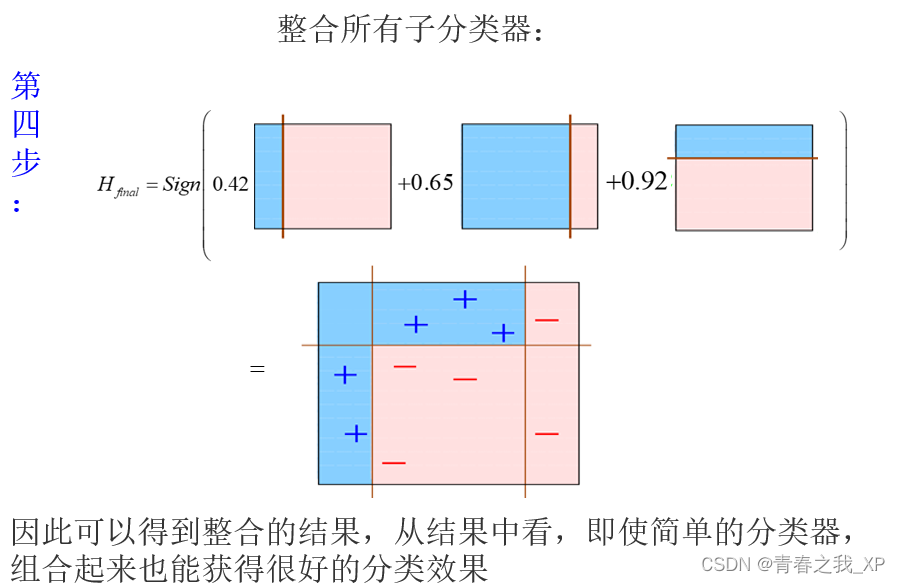
相关文章:

【机器学习系列】深入理解集成学习:从Bagging到Boosting
目录 一、集成方法的一般思想 二、集成方法的基本原理 三、构建集成分类器的方法 常见的有装袋(Bagging)和提升(Boosting)两种方法 方法1 :装袋(Bagging) Bagging原理如下图: …...

用FFMPEG对YUV序列进行编辑的笔记
还是单独开一个吧 每次找挺烦的 播放YUV序列 ffmpeg -f rawvideo -pix_fmt yuv420p -s 3840x2160 -i "Wood.yuv" -vf "scale1280x720" -c:v rawvideo -pix_fmt yuv420p -f sdl "Wood"4K序列转720P ffmpeg -f rawvideo -pix_fmt yuv420p -s 38…...

智能投顾:重塑金融理财市场,引领行业新潮流
一、引言 在数字化浪潮的推动下,金融行业正经历着前所未有的变革。其中,智能投顾作为金融科技的重要分支,以其高效、便捷和个性化的服务,逐渐成为金融理财市场的新宠。本文旨在探讨智能投顾如何引领金融理财新潮流,通过丰富的案例及解决方案,展示其独特的魅力和价值。 二…...

iOS18 新变化提前了解,除了AI还有这些变化
iOS 18即将在不久的将来与广大iPhone用户见面,这次更新被普遍认为是苹果历史上最重要的软件更新之一。据多方报道和泄露的消息,iOS 18将带来一系列全新的功能和改进,包括在人工智能领域的重大突破、全新的设计元素以及增强的性能和安全性。现…...

力扣算法题:多数元素 --多语言实现
无意间看到,力扣存算法代码居然还得升级vip。。。好吧,我自己存吧 golang: func majorityElement(nums []int) int {count : 0condidate : 0for _,val : range nums {if count 0 {condidate valcount 1} else if val condidate {count} …...

[Kubernetes] 容器运行时 Container Runtime
文章目录 1.容器运行时(Container Runtime)2.容器运行时接口3.容器运行时层级4.容器运行时比较5.强隔离容器6.K8S为何难以实现真正的多租户 1.容器运行时(Container Runtime) Container Runtime 是运行于 k8s 集群每个节点中,负责容器的整个生命周期。Docker 就目前…...

10进制与二、八、十六进制的转换
x进制转10进制 1、如八进制数123,通过把每一位数字和8的指数级进行相乘 1 * 8^2 2 * 8^1 3 * 8^01 * 64 2 * 8 3 * 164 16 383 2、十六进制1A3 1 * 16^2 A(即10) * 16^1 3 * 16^01 * 256 10 * 16 3 * 1256 160 3419 3、二进制1010 1 * 2^3 0 * 2…...

日常实习-小米计算机视觉算法岗面经
文章目录 流程问题请你写出项目中用到的模型代码,Resnet50(1)网络退化现象:把网络加深之后,效果反而变差了(2)过拟合现象:训练集表现很棒,测试集很差 把你做的工作里面的…...
string模拟实现)
(C++)string模拟实现
string底层是一个是字符数组 为了跟库里的string区别,所以定义一个命名空间将类string包含 一、构造 1.构造函数 注意:将char*传给const char*是范围缩小,因此只能1:1构造一个 strlen遇到nullptr解引用会报错,因此…...
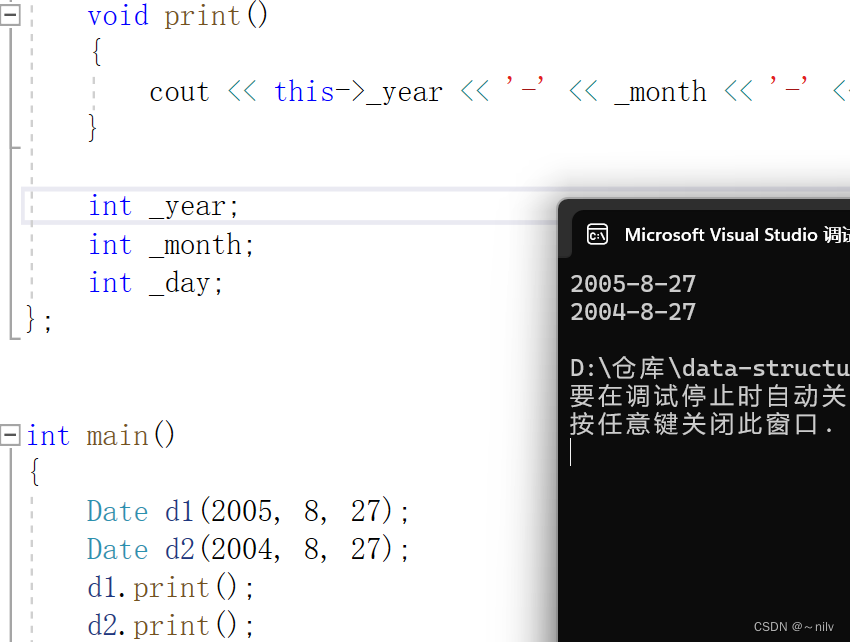
类和对象的学习总结(一)
面向对象和面向过程编程初步认识 C语言是面向过程的,关注过程(分析求解问题的步骤) 例如:外卖,关注点菜,接单,送单等 C是面向对象的,关注对象,把一件事拆分成不同的对象&…...

力扣22. 括号生成
数字 n 代表生成括号的对数,请你设计一个函数,用于能够生成所有可能的并且有效的括号组合。 示例 1:输入:n 3 输出:["((()))","(()())","(())()","()(())","()()(…...

检测窗口是否最大化兼容 Win10/11
检测窗口是否最大化(窗口覆盖或独占全屏)兼容 Win10/11 问题描述 在 Win10/11 上有很多 UWP 进程,检测窗口是否最大化将迎来新的挑战。这些窗口以其不能够使用 Win32 的 IsWindowVisible 获取窗口可见性为特征。此时,必须使用 D…...
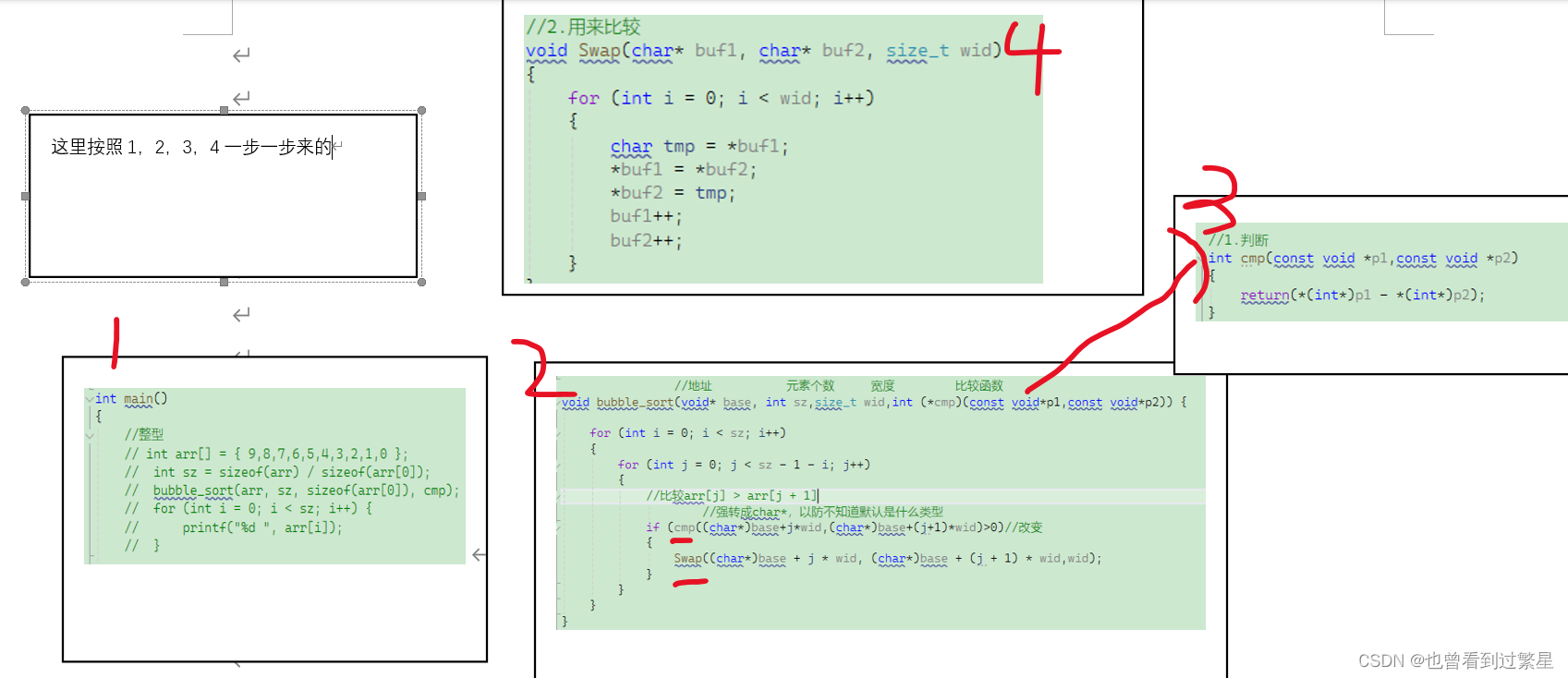
【qsort函数】
前言 我们要学习qsort函数并利用冒泡函数仿照qsort函数 首先我们要了解一下qsort(快速排序) 这是函数的的基本参数 void qsort (void* base, size_t num, size_t size,int (*compar)(const void*,const void*)); 简单解释一下 base:指向…...

python类元编程示例-使用类型注解来检查转换属性值的类框架
用三种方式实现使用类型注解来检查转换属性值的类框架 1 __init_subclass__方式 1.1 代码实现 from collections.abc import Callable # <1> from typing import Any, NoReturn, get_type_hints from typing import Dict, Typeclass Field:def __init__(self, name: …...
 和 rjust())
Python3 笔记:字符串的 zfill() 和 rjust()
1、zfill() 方法返回指定长度的字符串,原字符串右对齐,前面填充0。 语法:str.zfill(width) width :指定字符串的长度。原字符串右对齐,前面填充0。 str1 2546 str2 2 print(str1.zfill(10)) # 运行结果࿱…...

SpringBoot项目启动提示端口号占用
Windows环境下,SpringBoot项目启动时报端口号占用: *************************** APPLICATION FAILED TO START ***************************Description:Web server failed to start. Port 8080 was already in use.Action:Identify and stop the proc…...
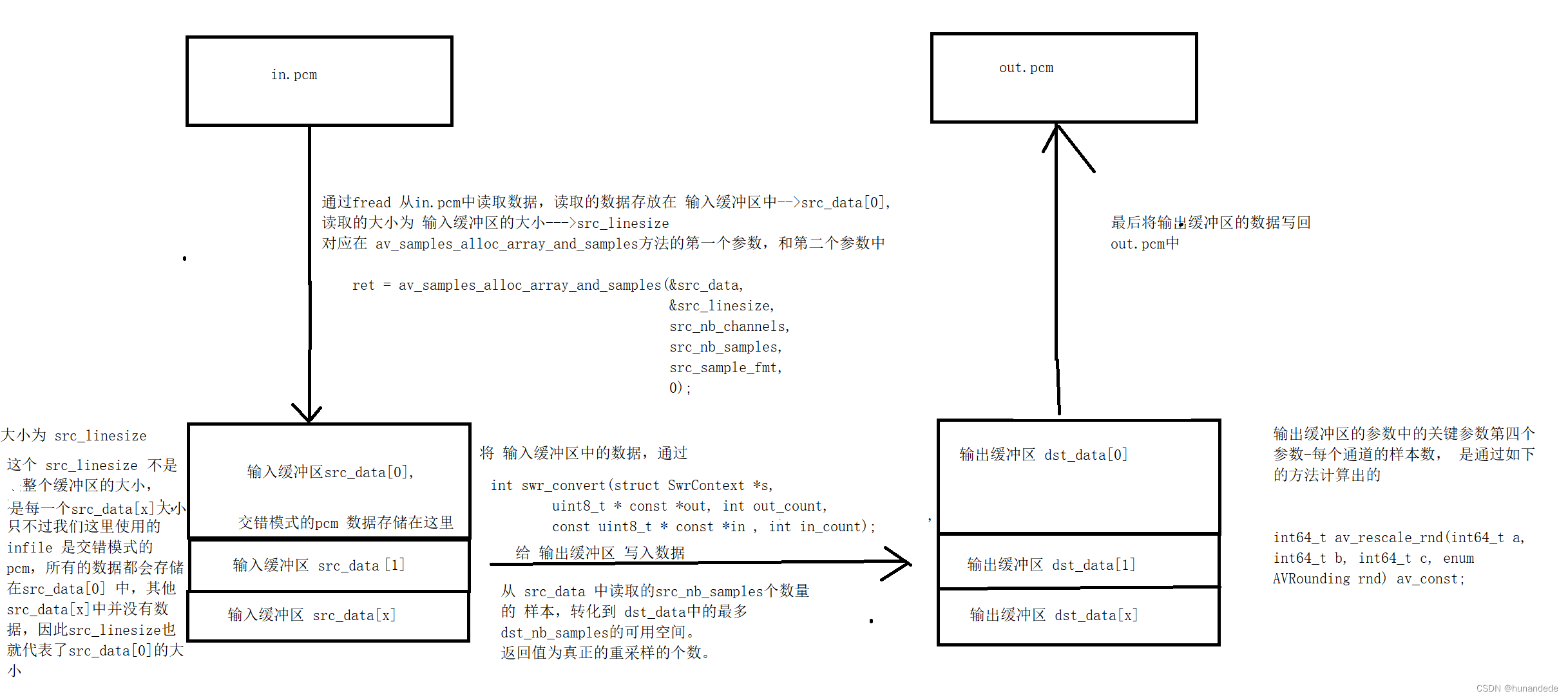
音视频开发23 FFmpeg 音频重采样
代码实现的功能 目的是 将: 一个采样率为 44100,采样通道为 2,格式为 AV_SAMPLE_FMT_DBL 的 in.pcm 数据 转换成 一个采样率为 48000,采样通道为 1,格式为 AV_SAMPLE_FMT_S16 的 out.pcm 数据 1.重采样 1.1 为什么要重…...
windows系统下安装fnm
由于最近做项目要切换多个node版本,查询了一下常用的有nvm和fnm这两种,对比了一下选择了fnm。 下载fnm 有两种方式,目前最新版本是1.37.0: 1.windows下打开powershell,执行以下命令下载fnm winget install Schniz.f…...
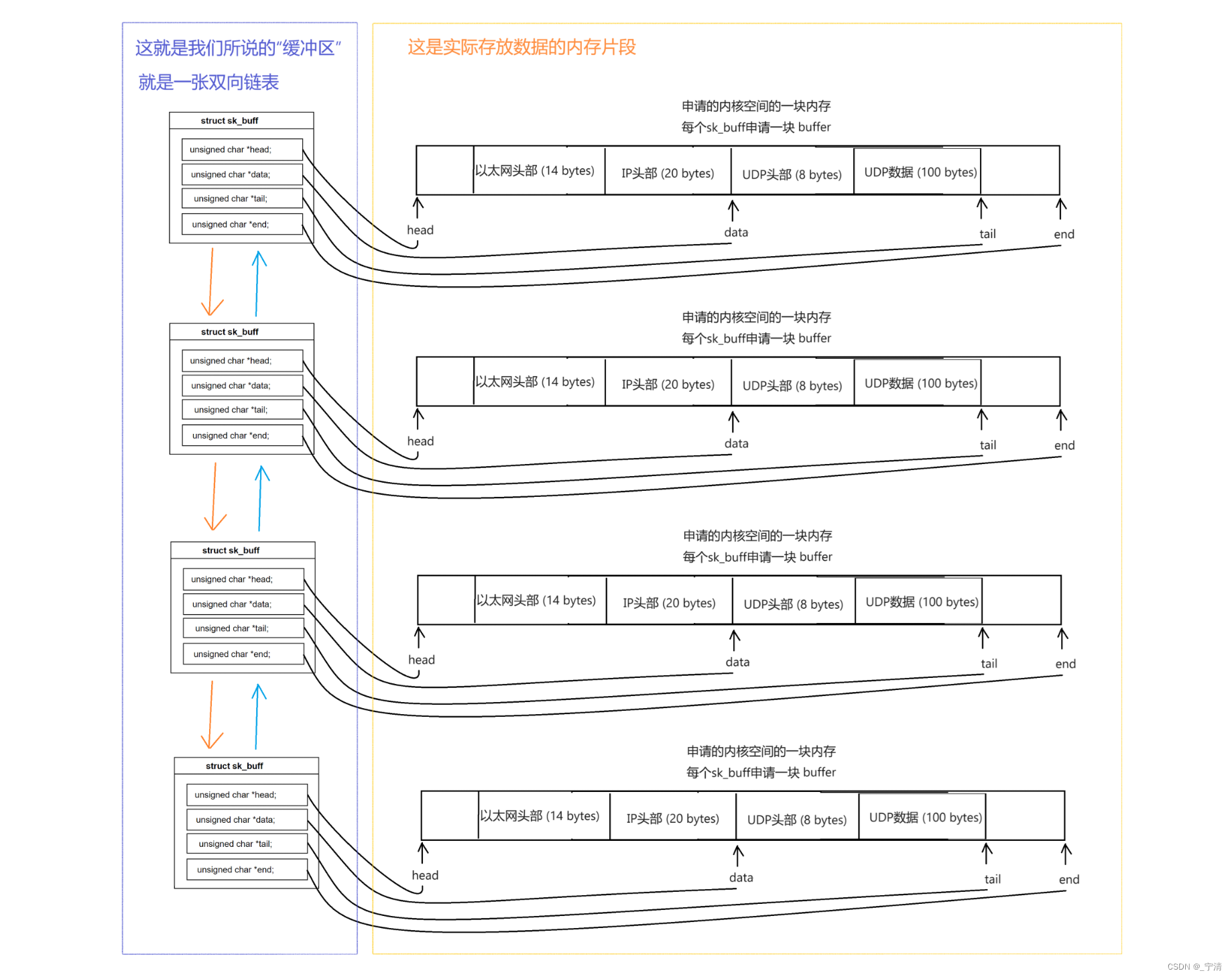
【Linux网络】传输层协议 - UDP
文章目录 一、传输层(运输层)运输层的特点复用和分用再谈端口号端口号范围划分认识知名端口号(Well-Know Port Number)两个问题① 一个进程是否可以绑定多个端口号?② 一个端口号是否可以被多个进程绑定? n…...
:源代码)
debugger(四):源代码
〇、前言 终于来到令人激动的源代码 level 了,这里将会有一些很有意思的算法,来实现源代码级别的调试,这将会非常有趣。 一、使用 libelfin 库 我们不可能直接去读取整个 .debug info 段来进行设置,这是没有必要的,…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

BLEU评分:机器翻译质量评估的黄金标准
BLEU评分:机器翻译质量评估的黄金标准 1. 引言 在自然语言处理(NLP)领域,衡量一个机器翻译模型的性能至关重要。BLEU (Bilingual Evaluation Understudy) 作为一种自动化评估指标,自2002年由IBM的Kishore Papineni等人提出以来,…...

WebRTC从入门到实践 - 零基础教程
WebRTC从入门到实践 - 零基础教程 目录 WebRTC简介 基础概念 工作原理 开发环境搭建 基础实践 三个实战案例 常见问题解答 1. WebRTC简介 1.1 什么是WebRTC? WebRTC(Web Real-Time Communication)是一个支持网页浏览器进行实时语音…...