基于JavaScript 实现近邻算法以及优化方案
前言
近邻算法(K-Nearest Neighbors,简称 KNN)是一种简单的、广泛使用的分类和回归算法。它的基本思想是:给定一个待分类的样本,找到这个样本在特征空间中距离最近的 k 个样本,这 k 个样本的多数类别作为待分类样本的类别。
本教程文章将详细讲解如何使用 JavaScript 实现一个简单的 KNN 算法,我们会从理论出发,逐步从零开始编写代码。
理论基础
距离度量
KNN 算法的核心是计算两个样本之间的距离,常用的距离度量方法有:
- 欧氏距离(Euclidean Distance)
- 曼哈顿距离(Manhattan Distance)
在本教程中,我们将使用最常见的欧氏距离来计算样本之间的距离。
欧氏距离公式如下:
[ d(p, q) = \sqrt{\sum_{i=1}^{n} (p_i - q_i)^2} ]
其中 ( p ) 和 ( q ) 是两个 n 维空间中的点, ( p_i ) 和 ( q_i ) 是这两个点在第 ( i ) 维的坐标。
算法步骤
- 计算距离:计算待分类样本与训练样本集中所有样本的距离。
- 排序:按距离从小到大对所有距离进行排序。
- 选择最近的 k 个样本:从排序后的结果中选择距离最近的 k 个样本。
- 投票:多数投票决定待分类样本的类别。
实现步骤
初始化数据
首先,我们需要一些样本数据来进行分类。假设我们有以下二维数据集:
const trainingData = [{ x: 1, y: 2, label: 'A' },{ x: 2, y: 3, label: 'A' },{ x: 3, y: 3, label: 'B' },{ x: 6, y: 5, label: 'B' },{ x: 7, y: 8, label: 'B' },{ x: 8, y: 8, label: 'A' },
];
计算距离
编写一个函数来计算两个点之间的欧氏距离:
function euclideanDistance(point1, point2) {return Math.sqrt(Math.pow(point1.x - point2.x, 2) +Math.pow(point1.y - point2.y, 2));
}
排序并选择最近的 k 个样本
编写一个函数,根据距离对样本进行排序,并选择距离最近的 k 个样本:
function getKNearestNeighbors(trainingData, testPoint, k) {const distances = trainingData.map((dataPoint) => ({...dataPoint,distance: euclideanDistance(dataPoint, testPoint)}));distances.sort((a, b) => a.distance - b.distance);return distances.slice(0, k);
}
多数投票
编写一个函数,通过多数投票来决定类别:
function majorityVote(neighbors) {const voteCounts = neighbors.reduce((acc, neighbor) => {acc[neighbor.label] = (acc[neighbor.label] || 0) + 1;return acc;}, {});return Object.keys(voteCounts).reduce((a, b) => voteCounts[a] > voteCounts[b] ? a : b);
}
主函数
最后,编写一个主函数来整合上述步骤,完成 KNN 算法:
function knn(trainingData, testPoint, k) {const neighbors = getKNearestNeighbors(trainingData, testPoint, k);return majorityVote(neighbors);
}
测试
现在我们来测试一下这个 KNN 实现:
const testPoint = { x: 5, y: 5 };
const k = 3;const result = knn(trainingData, testPoint, k);
console.log(`The predicted label for the test point is: ${result}`);
运行这个代码,你会得到预测的类别。
优化方案
虽然我们已经实现了一个基本的 KNN 算法,但在实际应用中,我们还可以进行一些优化和扩展,使其更加高效和实用。
优化距离计算
在大数据集上,计算每个点之间的欧氏距离可能会很耗时。我们可以通过一些高效的数据结构如 KD 树(K-Dimensional Tree)来进行快速邻近搜索。以下是一个简单的 KD 树的实现示例:
class KDTree {constructor(points, depth = 0) {if (points.length === 0) {this.node = null;return;}const k = 2; // 2Dconst axis = depth % k;points.sort((a, b) => a[axis] - b[axis]);const median = Math.floor(points.length / 2);this.node = points[median];this.left = new KDTree(points.slice(0, median), depth + 1);this.right = new KDTree(points.slice(median + 1), depth + 1);}nearest(point, depth = 0, best = null) {if (this.node === null) {return best;}const k = 2;const axis = depth % k;let nextBranch = null;let oppositeBranch = null;if (point[axis] < this.node[axis]) {nextBranch = this.left;oppositeBranch = this.right;} else {nextBranch = this.right;oppositeBranch = this.left;}best = nextBranch.nearest(point, depth + 1, best);const dist = euclideanDistance(point, this.node);if (best === null || dist < euclideanDistance(point, best)) {best = this.node;}if (Math.abs(point[axis] - this.node[axis]) < euclideanDistance(point, best)) {best = oppositeBranch.nearest(point, depth + 1, best);}return best;}
}const points = trainingData.map(point => [point.x, point.y, point.label]);
const kdTree = new KDTree(points);const nearestPoint = kdTree.nearest([testPoint.x, testPoint.y]);
console.log(`The nearest point is: ${nearestPoint[2]}`);
考虑不同距离度量
不同的距离度量方法在不同的场景下可能会有不同的效果。除了欧氏距离外,还可以尝试以下几种距离度量方法:
- 曼哈顿距离(Manhattan Distance)
- 闵可夫斯基距离(Minkowski Distance)
- 切比雪夫距离(Chebyshev Distance)
我们可以编写一些函数来实现这些距离度量方法,并在主函数中进行选择:
function manhattanDistance(point1, point2) {return Math.abs(point1.x - point2.x) + Math.abs(point1.y - point2.y);
}function minkowskiDistance(point1, point2, p) {return Math.pow(Math.pow(Math.abs(point1.x - point2.x), p) +Math.pow(Math.abs(point1.y - point2.y), p),1 / p);
}function chebyshevDistance(point1, point2) {return Math.max(Math.abs(point1.x - point2.x), Math.abs(point1.y - point2.y));
}
调整 k 值
选择合适的 k 值对算法的性能至关重要。过小的 k 值可能导致过拟合,而过大的 k 值可能导致欠拟合。一个常见的做法是通过交叉验证来选择最优的 k 值。
处理多维数据
在实际应用中,数据通常是多维的。我们的算法已经可以处理二维数据,但对于多维数据,只需稍微调整距离计算函数即可:
function euclideanDistanceND(point1, point2) {let sum = 0;for (let i = 0; i < point1.length; i++) {sum += Math.pow(point1[i] - point2[i], 2);}return Math.sqrt(sum);
}
代码重构
为了更好地组织代码,我们可以将不同的功能模块化:
class KNN {constructor(k = 3, distanceMetric = euclideanDistance) {this.k = k;this.distanceMetric = distanceMetric;}fit(trainingData) {this.trainingData = trainingData;}predict(testPoint) {const neighbors = this.getKNearestNeighbors(testPoint);return this.majorityVote(neighbors);}getKNearestNeighbors(testPoint) {const distances = this.trainingData.map((dataPoint) => ({...dataPoint,distance: this.distanceMetric(dataPoint, testPoint)}));distances.sort((a, b) => a.distance - b.distance);return distances.slice(0, this.k);}majorityVote(neighbors) {const voteCounts = neighbors.reduce((acc, neighbor) => {acc[neighbor.label] = (acc[neighbor.label] || 0) + 1;return acc;}, {});return Object.keys(voteCounts).reduce((a, b) => voteCounts[a] > voteCounts[b] ? a : b);}
}// 测试代码
const knnClassifier = new KNN(3, euclideanDistance);
knnClassifier.fit(trainingData);
const predictedLabel = knnClassifier.predict(testPoint);
console.log(`The predicted label for the test point is: ${predictedLabel}`);
通过这种方式,我们不仅提高了代码的可读性和可维护性,还为将来更复杂的扩展和优化打下了基础。
结语
KNN 算法简单易懂,适用于很多分类问题,特别是在数据规模不大时。然而,KNN 的计算复杂度较高,尤其在高维数据和大规模数据集上,因此在实际应用中常常需要结合其他技术进行优化。
相关文章:

基于JavaScript 实现近邻算法以及优化方案
前言 近邻算法(K-Nearest Neighbors,简称 KNN)是一种简单的、广泛使用的分类和回归算法。它的基本思想是:给定一个待分类的样本,找到这个样本在特征空间中距离最近的 k 个样本,这 k 个样本的多数类别作为待…...

移动端适配和响应式页面中的常用单位
在移动端适配和响应式页面中,一般采用以下几种单位: 百分比(%):百分比单位是相对于父元素的大小计算的。它可以用于设置宽度、高度、字体大小等属性,使得元素能够随着父元素的大小自动调整。百分比单位在响…...

麒麟v10系统arm64架构openssh9.7p1的rpm包
制作openssh 说明 理论上制作的多个rpm在arm64架构(aarch64)都适用 系统信息:4.19.90-17.ky10.aarch64 GNU/Linux 升级前备份好文件/etc/ssh、/etc/pam.d等以及开启telnet 升级后确认正常后关闭telnet 在之前制作过openssh-9.5p1基础上继续…...

刚刚❗️德勤2025校招暑期实习测评笔试SHL测评题库已发(答案)
📣德勤 2024暑期实习测评已发,正在申请的小伙伴看过来哦👀 ㊙️本次暑期实习优先考虑2025年本科及以上学历的毕业生,此次只有“审计及鉴定”“税务与商务咨询”两个部门开放了岗位~ ⚠️测评注意事项: ὄ…...

python对视频进行帧处理以及裁减部分区域
视频截取帧 废话不多说直接上代码: from cv2 import VideoCapture from cv2 import imwrite# 定义保存图片函数 # image:要保存的图片名字 # addr;图片地址与相片名字的前部分 # num: 相片,名字的后缀。int 类型 def save_image(image, add…...

Python栈的编程题目
你好,我是悦创。 下面是三道关于栈的编程题目,适合不同难度级别的练习: 1. 有效的括号(简单) 题目描述: 给定一个只包括 (,),{,},[ 和 ] 的字符串…...
ROS云课三分钟外传之CoppeliaSim_Edu_V4_1_0_Ubuntu16_04
三分钟热度试一试吧,走过路过不要错过。 参考之前: 从云课五分钟到一分钟之v-rep_pro_edu_v3_6_2-CSDN博客 git clone https://gitcode.net/ZhangRelay/v-rep_pro_edu_v3_6_2_ubuntu16_04.gittar -xf v-rep_pro_edu_v3_6_2_ubuntu16_04/V-REP_PRO_EDU…...

day28回溯算法part04| 93.复原IP地址 78.子集 90.子集II
**93.复原IP地址 ** 本期本来是很有难度的,不过 大家做完 分割回文串 之后,本题就容易很多了 题目链接/文章讲解 | 视频讲解 class Solution { public:vector<string> result;// pointNum记录加入的点的数量,其等于3的时候停止void b…...

SpringBoot项目启动时“jar中没有主清单属性”异常
资料参考 Spring Boot 启动时 “jar中没有主清单属性” 异常 - spring 中文网 (springdoc.cn) 实际解决 更详细的参考以上,我这边的话只需要在 pom文件 中加上 spring-boot-maven-plugin 插件就能解决该异常,具体如下: <build><p…...

vAttention:用于在没有Paged Attention的情况下Serving LLM
文章目录 0x0. 前言(太长不看版)0x1. 摘要0x2. 介绍&背景0x3. 使用PagedAttention模型的问题0x3.1 需要重写注意力kernel0x3.2 在服务框架中增加冗余0x3.3 性能开销0x3.3.1 GPU上的运行时开销0x3.3.2 CPU上的运行时开销 0x4. 对LLM服务系统的洞察0x5…...

Python实现Stack
你好,我是悦创。 Python 中的栈结构是一种后进先出(LIFO, Last In, First Out)的数据结构,这意味着最后添加到栈中的元素将是第一个被移除的。栈通常用于解决涉及到反转、历史记录和撤销操作等问题。在 Python 中,你可…...
分布式存储)
Helm在线部署Longhorn(1.6.0版本)分布式存储
环境依赖: k8s (版本大于等于v1.21版本)、helm工具 安装前准备 k8s worker 节点都需要执行 yum -y --setopttsflagsnoscripts install iscsi-initiator-utils echo "InitiatorName$(/sbin/iscsi-iname)" > /etc/iscsi/initiatorname.iscsi systemctl …...
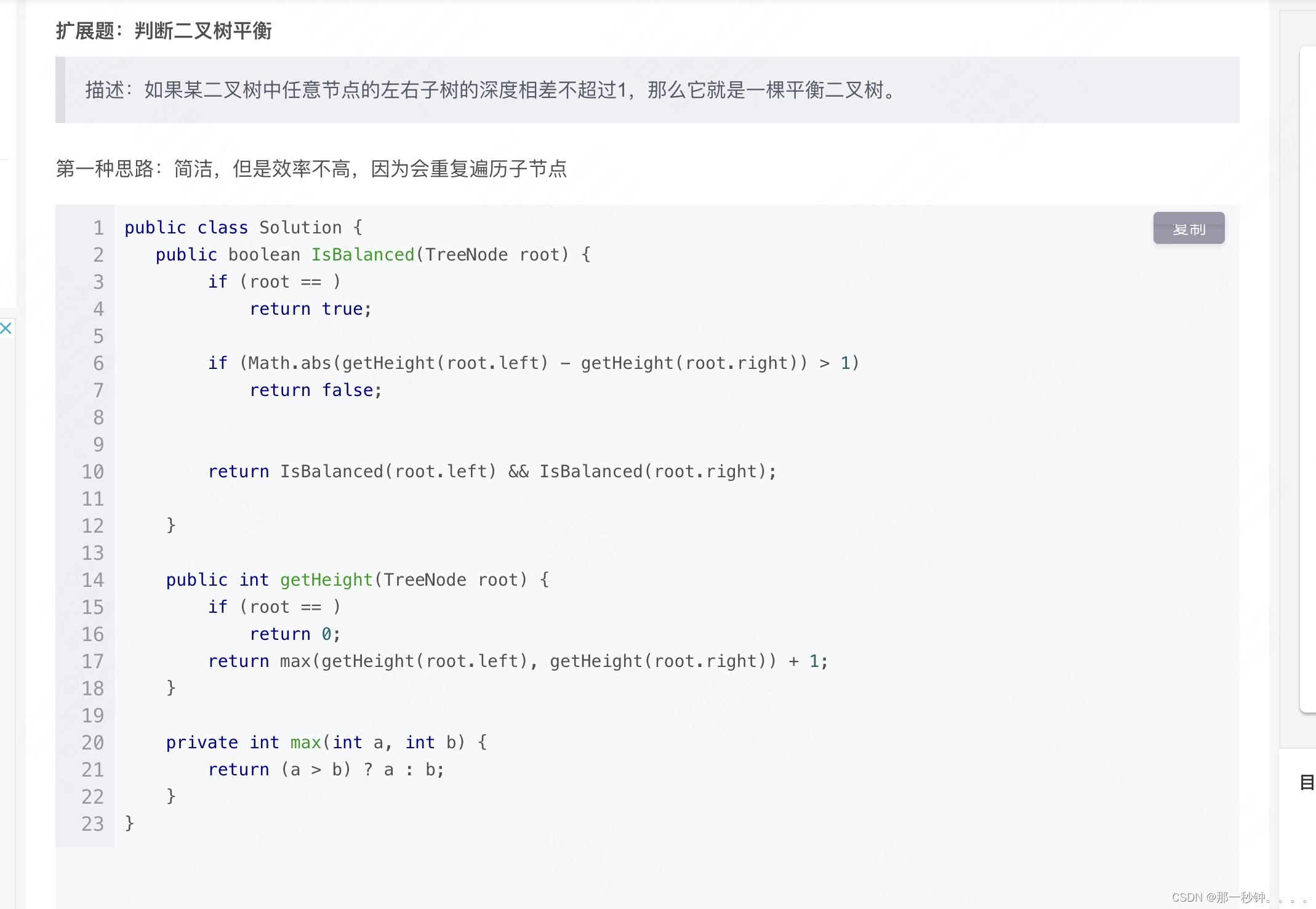
算法题目学习汇总
1、二叉树前中后序遍历:https://blog.csdn.net/cm15835106905/article/details/124699173 2、输入一棵二叉搜索树,将该二叉搜索树转换成一个排序的双向链表。要求不能创建任何新的结点,只能调整树中结点指针的指向。 public class Solution {private Tr…...
DockerCompose中部署Jenkins(Docker Desktop在windows上数据卷映射)
场景 DockerJenkinsGiteeMaven项目配置jdk、maven、gitee等拉取代码并自动构建以及遇到的那些坑: DockerJenkinsGiteeMaven项目配置jdk、maven、gitee等拉取代码并自动构建以及遇到的那些坑_jenkins的安装以及集成jdkgitmaven 提示警告-CSDN博客 Windows10(家庭版…...

吊车报警的工作原理和使用场景_鼎跃安全
在现代建筑施工过程中,经常使用大型机械设备,如挖掘机、吊车、打桩机等,这些设备在施工过程中发挥着越来越重要的作用;同时,这些设备的作业频繁进行作业,对于接触到高压电线的风险也随之增加。大型机械设备…...

Spring5
文章目录 1. Spring 是什么?2. IoC3. Spring Demo4. IoC 创建对象的方式 / DI 方式注入的默认参数在哪里设定? 5. Spring 配置tx:annotation-driven 用于启用基于注解的事务管理 6. Bean的作用域7. 在Spring中有三种自动装配的方式1. 在xml中显式的配置2. 在java中…...

vue面试题二
一、请解释Vue中的双向数据绑定是什么? Vue中的双向数据绑定是一种机制,它使得数据的变化能够自动反映在用户界面上,同时用户界面中的输入也能够自动更新数据。这种机制实现了数据层(Model)和视图层(View&…...

软件设计师笔记-程序语言基础知识
编程语言之间的翻译形式 编程语言之间的翻译形式主要有三种:汇编、解释和编译。这三种方式在将源代码转换为机器可执行的代码时,有着各自的特点和流程。 汇编: 定义:汇编是低级语言(如汇编语言)到机器语言的一种翻译方式。汇编语言是为特定计算机或计算机系列设计的一种…...

在Windows上安装VMWare Pro 16.2(虚拟机)并从零安装CentOS 7.6镜像过程记录
本文详细记录了在Windows的VMWare Workstation Pro 16.2中安装CentOS 7.6 的过程,非常适合新手从零开始一步步安装。 文章目录 一、安装VMWare Workstation Pro 16.2并激活二、安装CentOS 7.62.1 下载CentOS7.6镜像文件2.2 创建新的虚拟机2.3 安装CentOS镜像一、安装VMWare Wo…...

NGINX之location和rewrite
一.NGINX常用的正则表达式 二.Location location作用:对访问的路径做访问控制或者代理转发 1.location 常用的匹配规则: 进行普通字符精确匹配,也就是完全匹配^~ / 表示普通字符匹配。使用前缀匹配。如果匹配成功,则不再匹配其它 …...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

Ubuntu Cursor升级成v1.0
0. 当前版本低 使用当前 Cursor v0.50时 GitHub Copilot Chat 打不开,快捷键也不好用,当看到 Cursor 升级后,还是蛮高兴的 1. 下载 Cursor 下载地址:https://www.cursor.com/cn/downloads 点击下载 Linux (x64) ,…...

6️⃣Go 语言中的哈希、加密与序列化:通往区块链世界的钥匙
Go 语言中的哈希、加密与序列化:通往区块链世界的钥匙 一、前言:离区块链还有多远? 区块链听起来可能遥不可及,似乎是只有密码学专家和资深工程师才能涉足的领域。但事实上,构建一个区块链的核心并不复杂,尤其当你已经掌握了一门系统编程语言,比如 Go。 要真正理解区…...

yaml读取写入常见错误 (‘cannot represent an object‘, 117)
错误一:yaml.representer.RepresenterError: (‘cannot represent an object’, 117) 出现这个问题一直没找到原因,后面把yaml.safe_dump直接替换成yaml.dump,确实能保存,但出现乱码: 放弃yaml.dump,又切…...

PH热榜 | 2025-06-08
1. Thiings 标语:一套超过1900个免费AI生成的3D图标集合 介绍:Thiings是一个不断扩展的免费AI生成3D图标库,目前已有超过1900个图标。你可以按照主题浏览,生成自己的图标,或者下载整个图标集。所有图标都可以在个人或…...

Mysql故障排插与环境优化
前置知识点 最上层是一些客户端和连接服务,包含本 sock 通信和大多数jiyukehuduan/服务端工具实现的TCP/IP通信。主要完成一些简介处理、授权认证、及相关的安全方案等。在该层上引入了线程池的概念,为通过安全认证接入的客户端提供线程。同样在该层上可…...

基于Uniapp的HarmonyOS 5.0体育应用开发攻略
一、技术架构设计 1.混合开发框架选型 (1)使用Uniapp 3.8版本支持ArkTS编译 (2)通过uni-harmony插件调用原生能力 (3)分层架构设计: graph TDA[UI层] -->|Vue语法| B(Uniapp框架)B --&g…...
