时间序列评价指标
评价指标
均方误差( M S E MSE MSE)
- 定义:预测值与实际值之间差异的平方和的平均值。
- 公式: ( M S E = 1 n ∑ i = 1 n ( y i − y ^ i ) 2 ) (MSE = \frac{1}{n}\sum_{i=1}^{n}(y_i - \hat{y}_i)^2) (MSE=n1∑i=1n(yi−y^i)2) 其中, ( y i ) (y_i) (yi)是实际值, ( y ^ i ) (\hat{y}_i) (y^i) 是预测值, ( n ) (n) (n) 是样本数量。
- 特点: M S E MSE MSE是最常用的评价指标之一,它直接反映了预测误差的大小。然而, M S E MSE MSE对异常值比较敏感。
平均绝对误差( M A E MAE MAE)
- 定义:预测值与实际值之间差异的绝对值的平均值。
- 公式: ( M A E = 1 n ∑ i = 1 n ∣ y i − y ^ i ∣ ) (MAE = \frac{1}{n}\sum_{i=1}^{n}|y_i - \hat{y}_i|) (MAE=n1∑i=1n∣yi−y^i∣)
- 特点:与 M S E MSE MSE相比, M A E MAE MAE对异常值不敏感。但是, M A E MAE MAE没有考虑误差的平方,可能会低估误差的大小。
平均绝对百分比误差( M A P E MAPE MAPE)
- 定义:预测值与实际值之间差异的绝对值与实际值的比值的平均值。
- 公式: ( M A P E = 1 n ∑ i = 1 n ∣ y i − y ^ i y i ∣ × 100 (MAPE = \frac{1}{n}\sum_{i=1}^{n}\left|\frac{y_i - \hat{y}_i}{y_i}\right| \times 100%) (MAPE=n1∑i=1n yiyi−y^i ×100(注意:当实际值为 0 0 0时, M A P E MAPE MAPE无法计算)
- 特点: M A P E MAPE MAPE考虑了实际值的大小,可以帮助评估模型的相对误差。但是,对于含有零值的数据集, M A P E MAPE MAPE可能不适用。
均方根误差( R M S E RMSE RMSE)
- 定义:均方误差的平方根。
- 公式: ( R M S E = 1 n ∑ i = 1 n ( y i − y ^ i ) 2 ) (RMSE = \sqrt{\frac{1}{n}\sum_{i=1}^{n}(y_i - \hat{y}_i)^2}) (RMSE=n1∑i=1n(yi−y^i)2)
- 特点: R M S E RMSE RMSE与 M S E MSE MSE类似,但它与实际值的单位相同,因此更加直观。然而, R M S E RMSE RMSE同样对异常值敏感。
决定系数(R-squared,通常表示为( R 2 R^2 R2))
是回归分析中用于量化模型预测能力的一个统计量。它表示模型中自变量对因变量变化的解释程度,即模型能够解释的因变量变异的比例。
-
定义
决定系数( R 2 R^2 R2)的范围在 0 0 0到 1 1 1之间,其中:
( R 2 = 1 R^2 = 1 R2=1):表示模型完美地拟合了数据,即所有的观测点都落在回归线上。
( R 2 = 0 R^2 = 0 R2=0):表示模型没有解释任何因变量的变异,模型的预测值与观测值的平均值没有区别。
( 0 < R 2 < 1 0 < R^2 < 1 0<R2<1):表示模型解释了部分但非全部的因变量变异。
- 计算方法
R 2 = 1 − ∑ i = 1 n ( y i − y ^ i ) 2 ∑ i = 1 n ( y i − y ˉ ) 2 R^2 = 1 - \frac{\sum_{i=1}^{n} (y_i - \hat{y}_i)^2}{\sum_{i=1}^{n} (y_i - \bar{y})^2} R2=1−∑i=1n(yi−yˉ)2∑i=1n(yi−y^i)2
其中:
( Sum of Squared Residuals (SSR) \text{Sum of Squared Residuals (SSR)} Sum of Squared Residuals (SSR)) 是预测值与实际值之差的平方和,也称为残差平方和( R e s i d u a l S u m o f S q u a r e s , R S S Residual Sum of Squares,RSS ResidualSumofSquares,RSS)。
( Total Sum of Squares (SST) \text{Total Sum of Squares (SST)} Total Sum of Squares (SST)) 是因变量实际值与其均值之差的平方和,也称为总平方和( T o t a l S u m o f S q u a r e s , T S S Total Sum of Squares,TSS TotalSumofSquares,TSS)。
- 解释
( R 2 R^2 R2)值越接近 1 1 1,说明模型的拟合效果越好,能够解释的因变量变异比例越高。但是,也需要注意以下几点:
( R 2 R^2 R2)的增加不一定意味着模型预测能力的实质性提高。在某些情况下,简单地增加模型中的变量 数量(即使这些变量与因变量没有真正的关联)也可能导致( R 2 R^2 R2)的增加,但这并不意味着模型的 实际预测能力有所提高。因此,需要谨慎地解释和比较不同模型的( R 2 R^2 R2)值。
( R 2 R^2 R2)值也受样本大小的影响。在样本量很大时,即使很小的效应也可能导致较高的(R^2)值。因 此,在比较不同数据集上的模型时,需要考虑到这一点。
在某些情况下,即使( R 2 R^2 R2)值较低,模型也可能具有实际预测价值。特别是在处理具有复杂非线性 关系或存在大量随机噪声的数据时,很难达到很高的( R 2 R^2 R2)值。因此,在评估模型时,还需要考虑 其他因素(如模型的稳健性、可解释性等)。
相关文章:

时间序列评价指标
评价指标 均方误差( M S E MSE MSE) 定义:预测值与实际值之间差异的平方和的平均值。公式: ( M S E 1 n ∑ i 1 n ( y i − y ^ i ) 2 ) (MSE \frac{1}{n}\sum_{i1}^{n}(y_i - \hat{y}_i)^2) (MSEn1∑i1n(yi−y^i)…...
Docker:安装 Orion-Visor 服务器运维的技术指南
请关注微信公众号:拾荒的小海螺 博客地址:http://lsk-ww.cn/ 1、简述 Orion-Visor 是一种用于管理和监控容器的工具。它提供了一个直观的界面,用于查看容器的状态、资源使用情况以及日志等信息。在这篇技术博客中,我们将介绍如何…...
HarmonyOS Next 系列之底部标签栏TabBar实现(三)
系列文章目录 HarmonyOS Next 系列之省市区弹窗选择器实现(一) HarmonyOS Next 系列之验证码输入组件实现(二) HarmonyOS Next 系列之底部标签栏TabBar实现(三) 文章目录 系列文章目录前言一、实现原理二、…...
mac怎么录制屏幕?这2个方法你值得拥有
在数字化时代,屏幕录制已经成为一种常见且重要的工具,无论是教学演示、游戏直播还是会议记录,屏幕录制都发挥着不可或缺的作用。对于Mac用户而言,如何高效、便捷地进行屏幕录制,是一个值得探讨的话题,可是很…...

爱德华三坐标软件ACdmis.AC-dmis密码注册机
爱德华三坐标软件 AC-DMIS 是一款功能强大的三坐标测量软件,具有以下特点: • 支持多种测量模式:包括接触式测量、非接触式测量、复合式测量等,可以满足不同类型工件的测量需求。 • 高精度测量:采用先进的测量算法和…...

计算机网络 期末复习(谢希仁版本)第3章
对于点对点的链路,目前使用得最广泛的数据链路层协议是点对点协议 PPP (Point-to-Point Protocol)。局域网的传输媒体,包括有线传输媒体和无线传输媒体两个大类,那么有线传输媒体有同轴电缆、双绞线和光纤;无线传输媒体有微波、红…...

代码随想录——数组
给定一个n个元素有序(升序)的整型数组nums和一个目标值target,写一个函数搜索nums中的target,如果目标值存在返回下标,否则返回-1. //这个题说实话从逻辑上来看实在是太简单了,但是为什么每一次我写起来都感…...
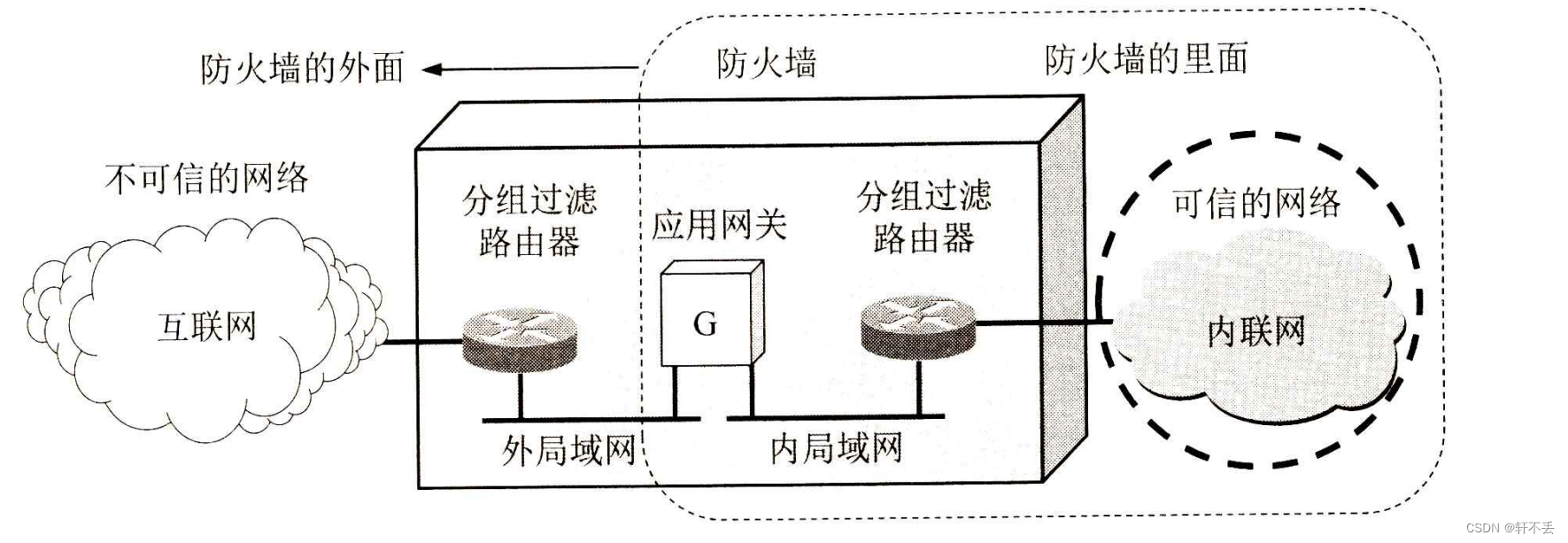
计算机网络7——网络安全4 防火墙和入侵检测
文章目录 一、系统安全:防火墙与入侵检测1、防火墙1)分组过滤路由器2)应用网关也称为代理服务器(proxy server), 二、一些未来的发展方向 一、系统安全:防火墙与入侵检测 恶意用户或软件通过网络对计算机系统的入侵或攻击已成为当今计算机安…...

html+CSS+js部分基础运用20
根据下方页面效果如图1所示,编写程序,代码放入图片下方表格内 图1.效果图 <!DOCTYPE html> <html lang"en"> <head> <meta charset"UTF-8"> <meta http-equiv"X-UA-Compatible" conte…...

ISO 19115-2:2019 附录C XML 模式实现
C.1 XML 模式 本文件中定义的 UML 模型的 XML 模式在 ISO/TS 19115-3 中定义的适当 XML 命名空间中提供。新增内容包括: 命名空间前缀模式文件名Metadata for ACquisition (mac)acquisitionInformationImagery.xsdMetadata for Resource Content (mrc)contentInfo…...
)
DevOps的原理及应用详解(一)
本系列文章简介: 在当今快速变化的商业环境中,企业对于软件交付的速度、质量和安全性要求日益提高。传统的软件开发和运维模式已经难以满足这些需求,因此,DevOps(Development和Operations的组合)应运而生&a…...
)
【冲刺秋招,许愿offer】第 三 天(水一天)
【冲刺秋招,许愿offer】第 二 天(水一天) 知识点牛客emo 知识点 今天端午,上午去摘杏下午理发,一天没咋看电脑。晚上刷刷LeetCode看看八股。 牛客 spring事务失效的情况 捕获到异常,自己手动处理 方法修…...
使用 C# 学习面向对象编程:第 6 部分
继承 亲爱的读者,继承意味着从源头继承一些东西。例如,儿子可以继承父亲的习惯。同样的概念也用于面向对象编程;它是 OOP 的第二大支柱。 继承允许创建一个新类,该新类继承另一个类或基类的属性,继承这些成员的类称为…...
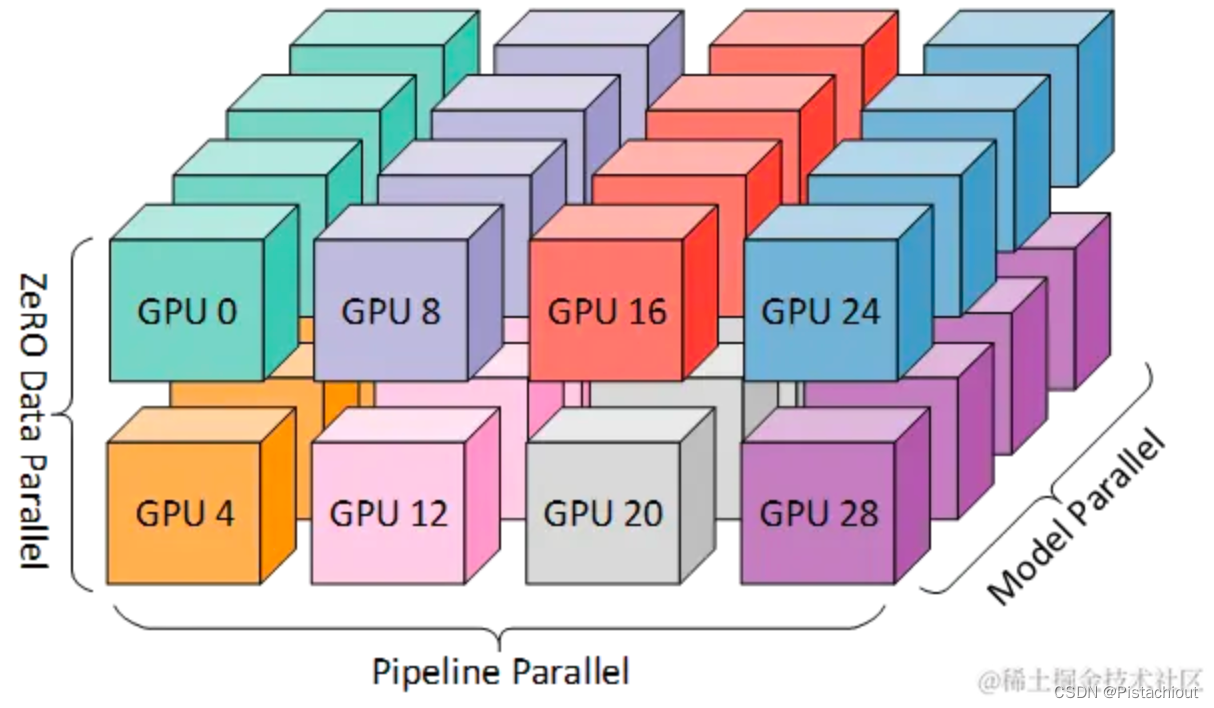
分布式训练基础入门
1.单节点训练 单节点训练也会转换为等价的并行训练,如在GPU内同一wrap内的32个Thread执行同一指令,但处理不同的数据。 训练程序往往实现了一个多层神经网络的执行过程。该神经网络的执行由一个计算图(Computational Graph)表示。…...
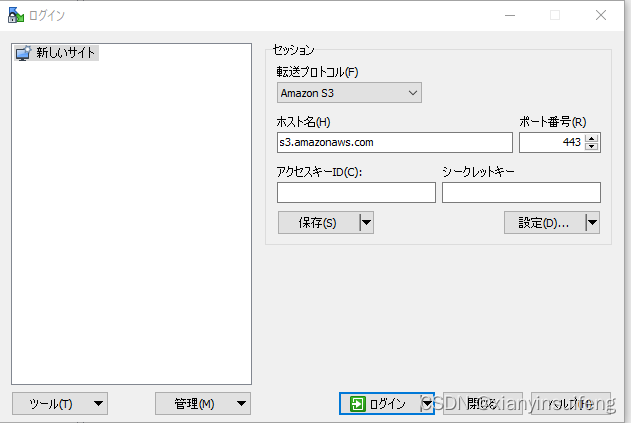
AWS S3存储桶中如何下载文件
AWS S3存储桶中如何下载文件 1.单个下载 AWS S3 控制台提供了下载单个文件的功能,但是不支持直接在控制台中进行批量下载文件。您可以通过以下步骤在 AWS S3 控制台上下载单个文件: 1.1登录 AWS 管理控制台。 1.2转到 S3 服务页面。 1.3单击…...
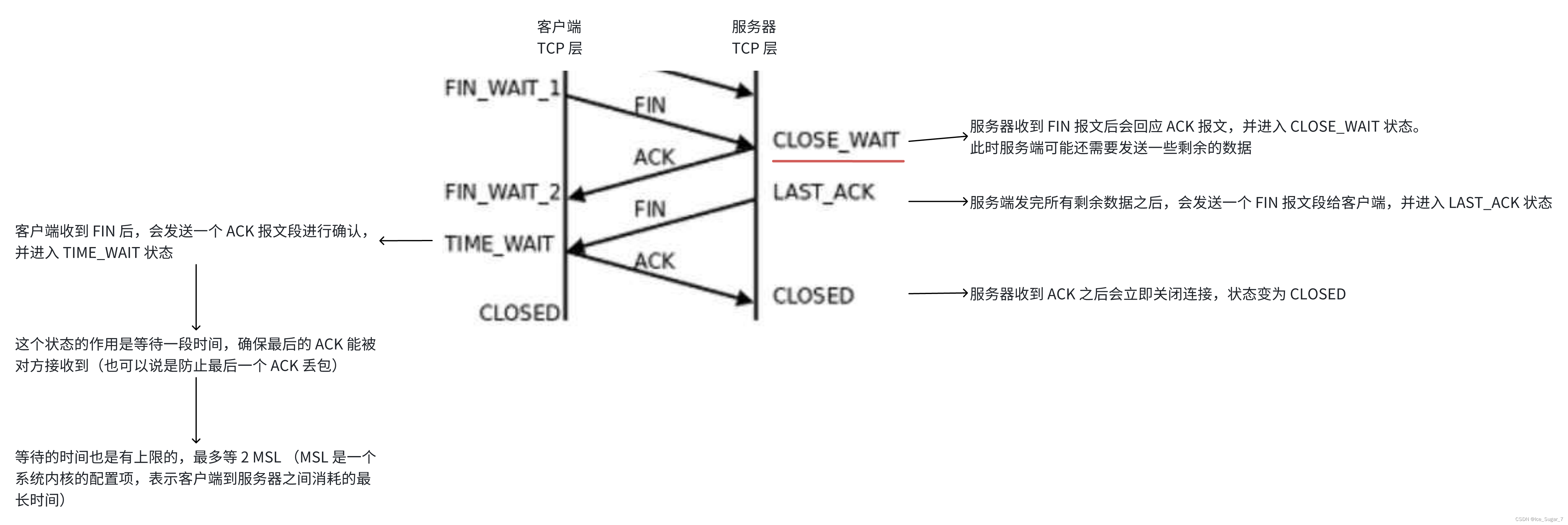
「网络原理」三次握手四次挥手
🎇个人主页:Ice_Sugar_7 🎇所属专栏:计网 🎇欢迎点赞收藏加关注哦! 三次握手&四次挥手 🍉连接管理🍌三次握手🍌意义🍌四次挥手🍌TCP 状态转换…...

第二十四章 SOAP 错误处理 - 发生故障时添加 WS-Addressing 标头元素
文章目录 第二十四章 SOAP 错误处理 - 发生故障时添加 WS-Addressing 标头元素%SOAP.Fault12.Code 属性SubcodeValue %SOAP.Fault12.Text 属性Textlang 发生故障时添加 WS-Addressing 标头元素 第二十四章 SOAP 错误处理 - 发生故障时添加 WS-Addressing 标头元素 %SOAP.Fault…...

CSS真题合集(一)
CSS真题合集(一) 1. 盒子模型1.1 盒子模型的基本组成1.2 盒子模型的实际大小1.3 盒子模型的两种类型1.4 设置盒子模型1.5 弹性盒子模型 2. BFC2.1 主要用途2.2 触发BFC的方法2.2 解决外边距的塌陷问题(垂直塌陷) 3. 响应式布局3.1…...
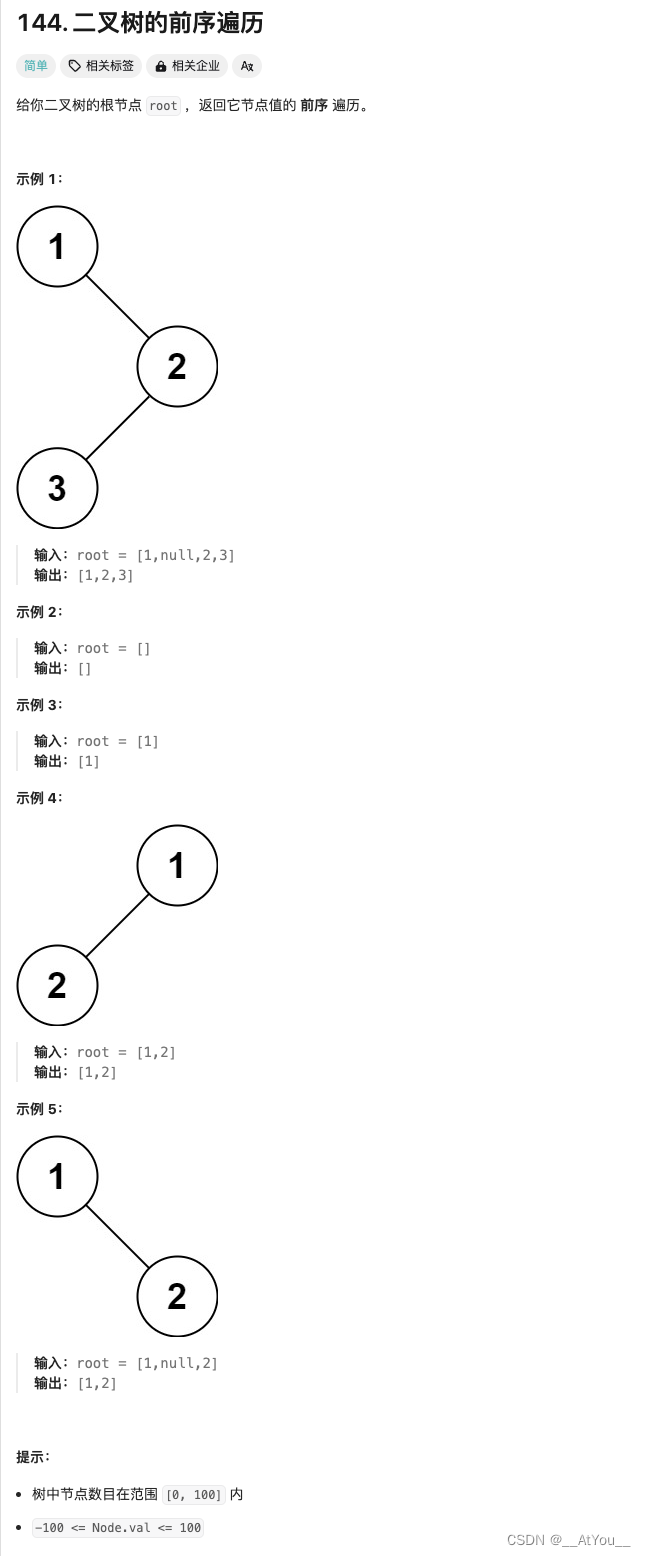
Golang | Leetcode Golang题解之第144题二叉树的前序遍历
题目: 题解: func preorderTraversal(root *TreeNode) (vals []int) {var p1, p2 *TreeNode root, nilfor p1 ! nil {p2 p1.Leftif p2 ! nil {for p2.Right ! nil && p2.Right ! p1 {p2 p2.Right}if p2.Right nil {vals append(vals, p1.V…...

离奇问题:java通过poi读取excel单元格的小数时会出错
问题 java通过poi读取excel单元格的小数时会出错,分析后发现是因为会损失精度。 处理的代码 /*** DataFormatter 直接new就行:DataFormatter df new DataFormatter();*/ private String getNumericCellValue(Cell cell, DataFormatter df) {String val…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

uniapp手机号一键登录保姆级教程(包含前端和后端)
目录 前置条件创建uniapp项目并关联uniClound云空间开启一键登录模块并开通一键登录服务编写云函数并上传部署获取手机号流程(第一种) 前端直接调用云函数获取手机号(第三种)后台调用云函数获取手机号 错误码常见问题 前置条件 手机安装有sim卡手机开启…...
)
安卓基础(Java 和 Gradle 版本)
1. 设置项目的 JDK 版本 方法1:通过 Project Structure File → Project Structure... (或按 CtrlAltShiftS) 左侧选择 SDK Location 在 Gradle Settings 部分,设置 Gradle JDK 方法2:通过 Settings File → Settings... (或 CtrlAltS)…...
