【Echarts系列】水平柱状图
【Echarts系列】水平柱状图
- 序
- 示例
- 数据格式
- 代码
序
为了节省后续开发学习成本,这个系列将记录我工作所用到的一些echarts图表。
示例
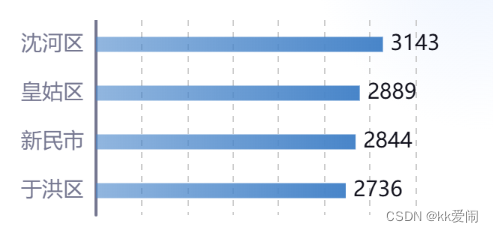
水平柱状图如图所示:
数据格式
data = [{'name': '于洪区','value': 2736},{'name': '新民市','value': 2844},{'name': '皇姑区','value': 2889},{'name': '沈河区','value': 3143}]
代码
Vue版本以及脚本语言的选择各有不同,核心内容主要是option,重点关注该部分内容即可。
<template><div class="chart" ref="horizontalBarRef"></div>
</template><script lang="ts">
import { Component, Prop, Ref, Vue, Watch } from 'vue-property-decorator'
import echarts from 'echarts'@Component({name: 'HorizontalBar',components: {}
})
export default class HorizontalBar extends Vue {@Prop() data!: any@Prop({ default: () => ['rgba(72, 133, 201, 0.6)', 'rgba(72, 133, 201, 1)']}) colors?: any[]@Ref() horizontalBarRef!: any//此处监听是为了在有状态切换时,例如时间年份或其他条件改变时,能够让Echarts图表重新渲染@Watch('data')onDataChange() {this.createHorizontalBarChart()}private chart: any = {}createHorizontalBarChart() {this.chart = echarts.init(this.horizontalBarRef)const data = this.datalet names = []let values = []data.forEach(item => {names.push(item.name)values.push(item.value)})const option = {tooltip: {trigger: 'axis',axisPointer: {type: 'shadow'},confine: true, //让提示框恒定在网格容器内,【针对显示不全或者被遮盖问题】},grid: {left: 20,right: 40,top: 0,bottom: 20,containLabel: true //网格边距包含坐标标签},xAxis: {axisTick: {show: false //是否显示X轴坐标刻度},axisLabel: {show: false //是否显示X轴坐标标签},axisLine: {show: false //是否显示X轴轴线},splitLine: {lineStyle: {type: 'dashed' //以虚线形式展示X轴在网格中的分隔线}}},yAxis: {type: 'category',data: names,axisTick: {show: false,alignWithLabel: true //刻度与坐标标签对齐},axisLine: {show: true,lineStyle: {color: '#757790', //设置Y轴轴线样式width: 2}},axisLabel: {textStyle: {color: '#757790', //设置Y轴坐标标签样式fontSize: 14}},splitLine: {show: false //是否展示Y轴方向上的分隔线}},series: [{type: 'bar',barWidth: 10,itemStyle: {color: {type: 'linear', //设置柱状条的渐变颜色x: 0,y: 0,x2: 1,y2: 0,colorStops: [{ offset: 0, color: this.colors[0] }, // 0% 处的颜色{ offset: 1, color: this.colors[1] } // 100% 处的颜色],global: false // 缺省为 false}},label: {show: true, //展示柱状条数值信息position: 'right',color: '#12121D',fontSize: 14},data: values}]}this.chart.setOption(option)}mounted() {this.createHorizontalBarChart()window.addEventListener('resize', this.chartResize)}beforeDestroy() {if (this.chart) {window.removeEventListener('resize', this.chartResize)this.chart.dispose()}}chartResize() {if (this.chart) {this.chart.resize()}}
}
</script>
<style lang="scss" scoped>
.chart {width: 100%;height: 300px;
}
</style>相关文章:

【Echarts系列】水平柱状图
【Echarts系列】水平柱状图 序示例数据格式代码 序 为了节省后续开发学习成本,这个系列将记录我工作所用到的一些echarts图表。 示例 水平柱状图如图所示: 数据格式 data [{name: 于洪区,value: 2736},{name: 新民市,value: 2844},{name: 皇姑区,…...

怎样把便签里的内容移到桌面?桌面便签软件使用方法
每次打开电脑,我总是被满屏的文件和图标弄得眼花缭乱。那些记录在各式各样便签里的重要事项,经常被埋没在这信息的海洋中,找起来真是头疼。想必很多人都有过这样的困扰:如何在繁杂的桌面环境中,一眼就看到自己需要提醒…...

量化入门:qmt获取可转债基本信息和行情数据
💻专业版获取可转债数据 今天将展示如何使用Python和QMT来获取可转债的实时数据和财务数据。 🔬 获取可转债基本信息 迅投的券商版和基础版都不支持可转债行情,投研专业版才支持,一年大概5000元。免费的券商版可参考QMT量化入门 投研专业版才有权限调用download_cb_d…...
AVL树 ---(C++)
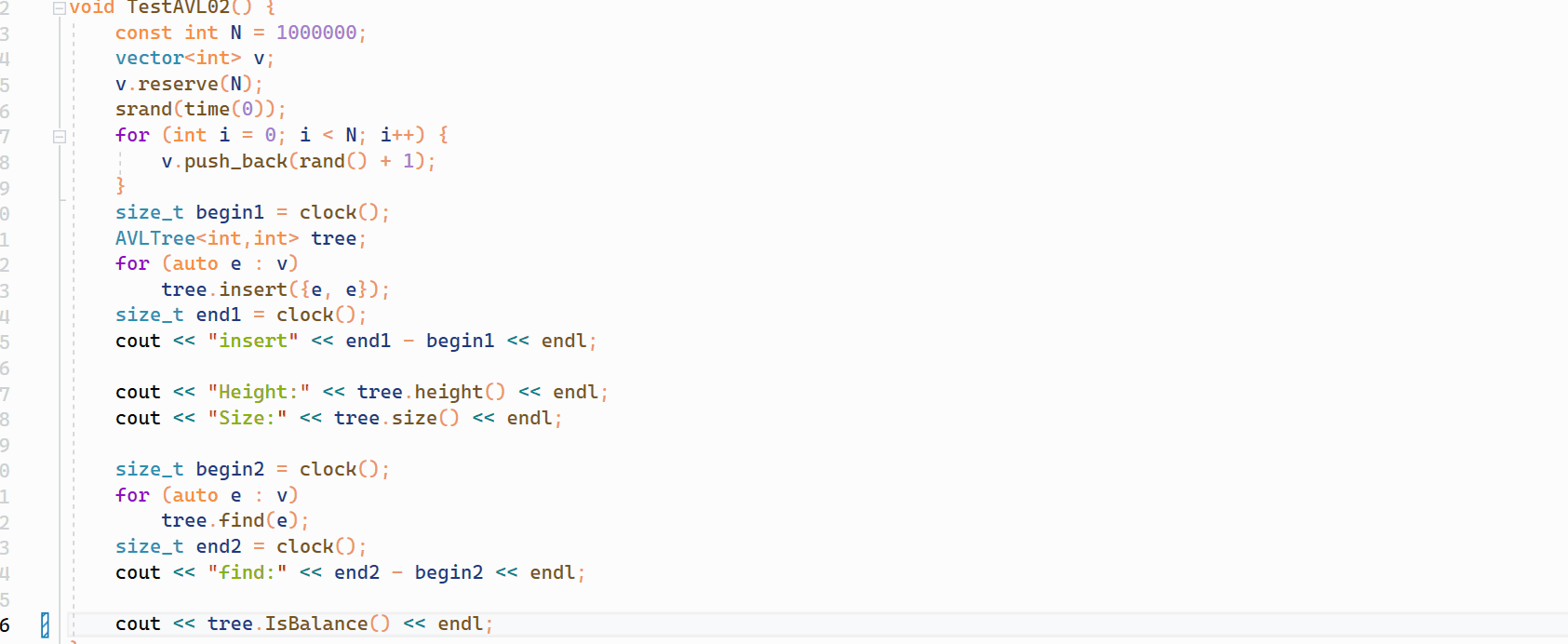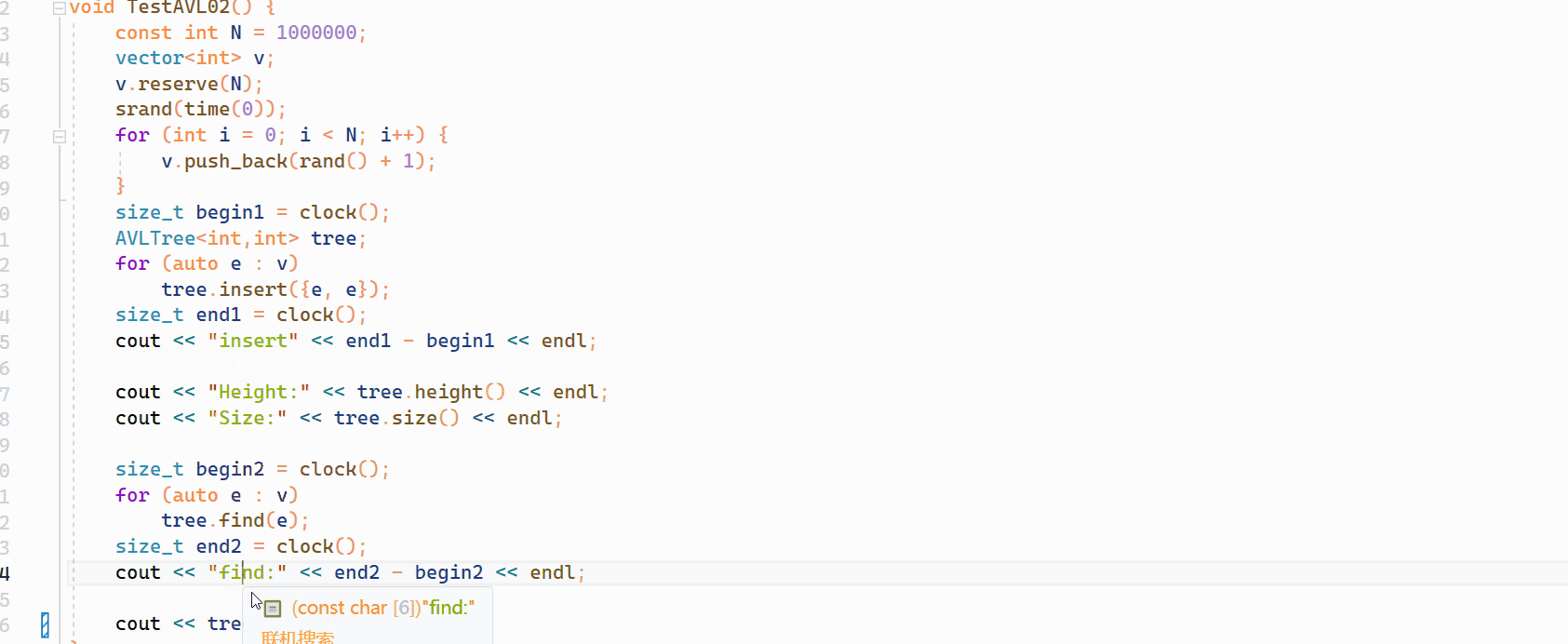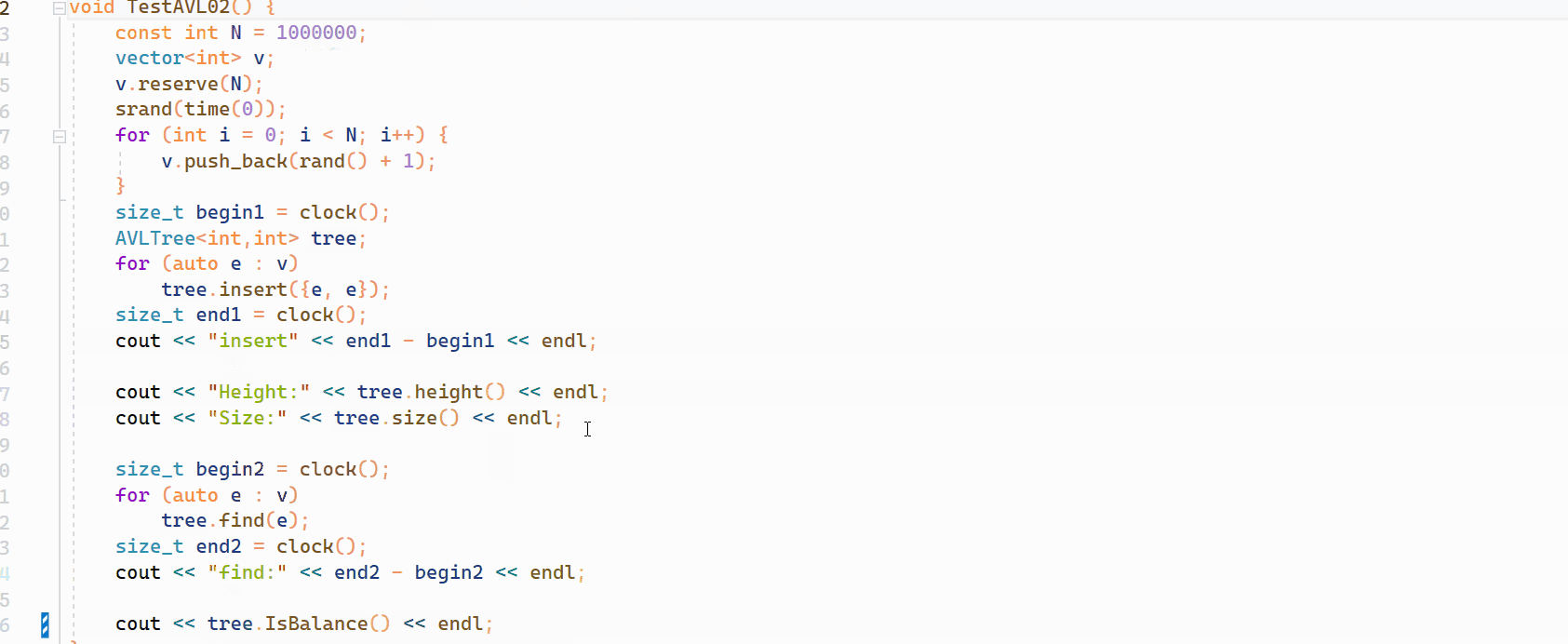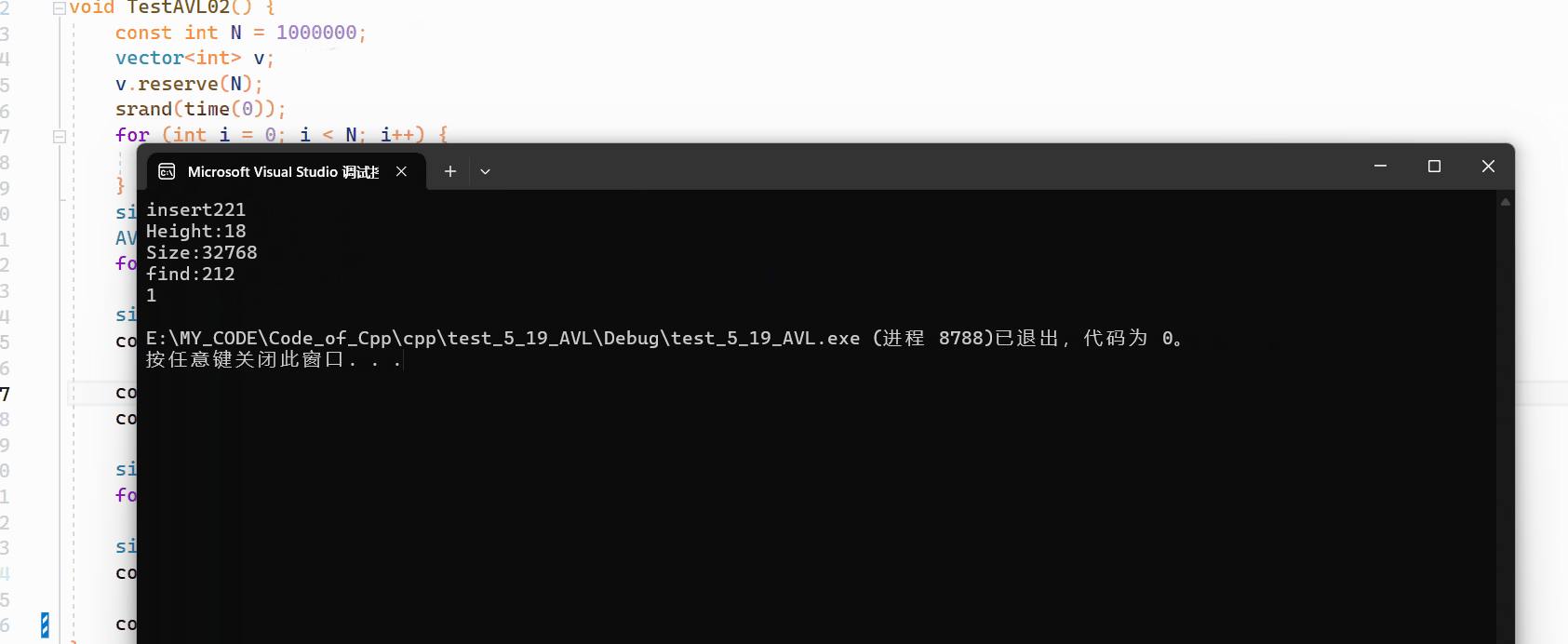
本篇讲全面的讲解 AVL 树的插入,旋转以及验证 AVL 树的性能(本篇未实现删除代码)。至于为什么会有 AVL 树,这是因为简单的二叉搜索树并不能直接的保证搜索的效率,因为当我们在二叉搜索树中插入一段有序的序列的时候&am…...
基于spring boot+MySQL 小区物业管理系统-计算机毕设 附源码37236
spring boot 小区物业管理系统 摘 要 在网络信息的时代,众多的软件被开发出来,给用户带来了很大的选择余地,而且人们越来越追求更个性的需求。在这种时代背景下,小区物业只能以客户为导向,以产品的持续创新作为小区物…...

Linux/Ubuntu/Debian常用服务管理命令
Linux/Ubuntu/Debian常用服务管理命令 在 Linux 系统中,服务管理是系统管理员日常维护工作的重要组成部分。通过一些常用的命令,我们可以查看服务状态、启动或停止服务、重启服务等。掌握这些命令,可以让系统管理工作更加高效和便捷。 1. s…...

Maven的三种项目打包方式——pom,jar,war的区别
1、pom:用在父级工程或聚合工程中,用来做jar包的版本控制,必须指明这个聚合工程的打包方式为pom。 聚合工程只是用来帮助其他模块构建的工具,本身并没有实质的内容。具体每个工程代码的编写还是在生成的工程中去写。 对于在父工程…...

[手游] 三色绘恋S Mobile Link
语音合成TTS: 文字转成语音的工具 WPS免登录一键修改器: 去除烦人的登录且能正常使用 故事简介: 深秋的雨季即将到来,正值那个为人所熟知的故事发生的前一年—— 地点:湖北省的重点高中,武汉师贰高校。 新学年开始,各…...

nss刷题(4)
1、[SWPUCTF 2021 新生赛]easyrce <?php error_reporting(0); highlight_file(__FILE__); if(isset($_GET[url])) { eval($_GET[url]); } ?> if(isset($_GET[url])) isset函数用来检测url变量是否存在;$_GET函数获取变量数据 eval($_GET[url]); eval函数用…...

iOS调整collectionViewCell顺序
效果图 原理 就是设置collectionView调整顺序的代理方法,这里要注意一点 调整过代理方法之后,一定要修改数据源,否则导致错乱。 还有就是在collectionView上面添加一个长按手势,在长按手势的不同阶段,调用collectionV…...

【回调函数】
1.回调函数是什么? 回调函数就是⼀个通过函数指针调用的函数。 如果你把函数的指针(地址)作为参数传递给另⼀个函数,当这个指针被用来调用其所指向的函数 时,被调用的函数就是回调函数。回调函数不是由该函数的实现方…...

找树左下角的值-力扣
本题个人认为不能叫做 找树左下角的值,左下角再怎么说也应当在树的左子树上,本题要求的节点是树最底层最左边的值。 首先想到的解法是对二叉树进行层序遍历,并记录本层第一个节点的值,当层序遍历结束时,此时记录的值即…...

【AI应用探讨】— Gemma2模型应用场景
目录 1. 金融风险管理 2. 营销策略优化 3. 医疗保健领域 4. 供应链管理 5. 人力资源管理 6. 自然语言处理(NLP) 7. 图像识别 8. 音频信号处理 9. 总结 1. 金融风险管理 场景描述:Gemma 2模型在金融领域可用于预测金融市场的波动性和…...
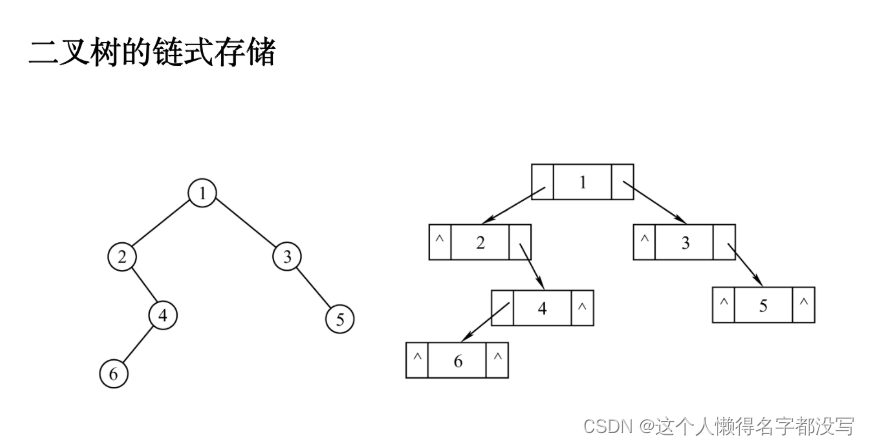
树二叉树
树 树是 n(n≥0)个结点的有限集。当 n 0时,称为空树。在任意一颗非空树中应满足: (1)有且仅有一个特定的称为根的结点。 (2)当 n > 1时,其余结点可分为 m&…...
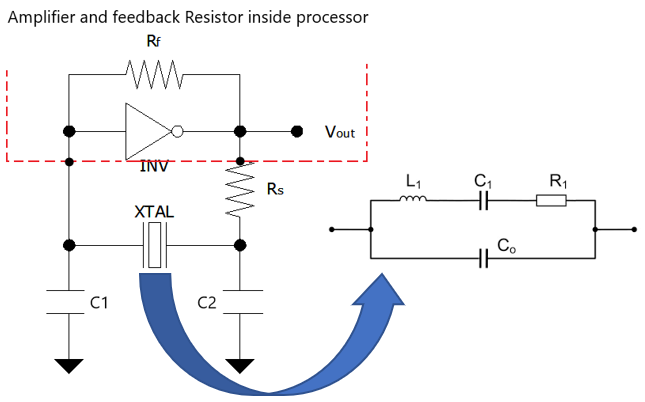
无源晶振振荡电路失效问题分析与解决策略
无源晶振(晶体谐振器)在电子设备中扮演着至关重要的角色,为数字电路提供稳定的时钟信号。然而,振荡电路一旦失效,可能会导致整个系统运行不正常。晶发电子将从三个主要方面分析无源晶振振荡电路失效的问题,…...

LIMS系统在汽车第三方检测实验室的应用
随着汽车行业的快速发展,汽车第三方检测实验室的工作量不断增加,对实验室的管理效率和数据准确性提出了更高的要求。LIMS系统的引入可以实现实验室的全面数字化管理,提高工作效率,降低运营成本,并提升数据质量与决策支…...

positivessl泛域名https证书
PositiveSSL,作为Sectigo旗下的子品牌,一直以来颁发的https数字证书产品性价比较高,适合大多数个人网站和中小型企业。其中,DV基础型的泛域名https证书以申请简单、颁发速度快、价格低受到众多用户的欢迎。今天就随SSl盾小编了解P…...

MySQL bin-log日志恢复数据
目录 一、开启二进制日志 二、检查二进制日志是否开启 三、使用二进制日志备份和恢复 使用二进制日志备份恢复前先创建备份: 应用二进制日志: 扩展用法: 四、常见命令和操作 五. 使用 mysqlbinlog 工具查看二进制日志 1. 查看二进制…...

Linux网络命令——netstat
netstat是Linux系统中非常有用的网络工具,被称为是网络监控中的军工刀,足见其地位。 传统上,它用于问题确定而不是性能测量,但是也可用于查看网络上的流量,以确定性能问题是否由于网络阻塞引起。 netstat用于显示与I…...

手机怎么压缩图片?通过三种压缩操作
手机怎么压缩图片?在智能手机日益普及的今天,拍照分享已成为日常生活的一部分。然而,高质量的照片往往占用较大的存储空间,且在网络上传输时速度较慢。那么,如何在手机上压缩图片呢?本文将介绍三种实用的手…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

LabVIEW双光子成像系统技术
双光子成像技术的核心特性 双光子成像通过双低能量光子协同激发机制,展现出显著的技术优势: 深层组织穿透能力:适用于活体组织深度成像 高分辨率观测性能:满足微观结构的精细研究需求 低光毒性特点:减少对样本的损伤…...

MySQL:分区的基本使用
目录 一、什么是分区二、有什么作用三、分类四、创建分区五、删除分区 一、什么是分区 MySQL 分区(Partitioning)是一种将单张表的数据逻辑上拆分成多个物理部分的技术。这些物理部分(分区)可以独立存储、管理和优化,…...
