代码随想录算法训练营第三十五天|1005.K次取反后最大化的数组和 134. 加油站 135. 分发糖果
LeetCode 1005.K次取反后最大化的数组和
题目链接:1005.K次取反后最大化的数组和
踩坑:没有
思路:数组里有正有负,肯定先对负数进行取反,且从小开始。如果所有负数都为正后还可以取反,则如果此时次数为奇数,将最小整数取反,如果为偶数,可以直接求和。
代码:
class Solution {
public:int largestSumAfterKNegations(vector<int>& nums, int k) {sort(nums.begin(), nums.end());for(int i = 0; i < nums.size(); i++){if(k != 0){if(nums[i] < 0){nums[i] = -nums[i];k--;}}else break;}sort(nums.begin(), nums.end());if(k % 2 != 0) nums[0] = -nums[0];int result = 0;for(int i = 0; i<nums.size(); i++){result = result + nums[i];}return result;}
};
LeetCode 134.加油站
题目链接:134.加油站
踩坑:看了视频
思路:感觉有点像钻了数学的空子,因为第一:所有gas-cost的差值的和小于0的话不会有解。第二:除了第一种情况,其他情况一定有解。所以解题过程就可以表示为如果当前站点会使计划失败(剩余的油为负数),那么只能将下一个站点作为起点。但是其中还是有很多隐藏逻辑以及节省的步骤可以辨析的。
代码:
class Solution {
public:int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {int curSum = 0;int totalSum = 0;int start = 0;for(int i = 0; i < gas.size(); i++){curSum += gas[i] - cost[i];totalSum += gas[i] - cost[i];if(curSum <0){start = i+1;curSum = 0;}}if(totalSum < 0) return -1;return start;}
};
LeetCode 135.分发糖果
题目链接:135.分发糖果
踩坑:以为分开考虑是以最小值为中心向左向右。
思路:从左向右遍历处理右孩子大于左孩子的情况,从右向左遍历处理左孩子大于右孩子的情况。初始的孩子分配一个糖果。最后取两种情况下的较大值,因为较小值肯定不满足另一种情况,至于为什么较大的值肯定满足两种情况并没有解释。。。
代码:
class Solution {
public:int candy(vector<int>& ratings) {vector<int> result(ratings.size(), 0);vector<int> t(ratings.size(), 0);result[0] = 1;t[t.size()-1] = 1;for(int i = 1; i < ratings.size(); i++){if(ratings[i] > ratings[i-1]) result[i] = result[i-1] + 1;else result[i] = 1;}for(int i = ratings.size()-2; i >= 0; i--){if(ratings[i] > ratings[i+1]){result[i] = max(result[i], t[i+1] + 1);t[i] = t[i+1] + 1;}else t[i] = 1;}int sum = 0;for(int i: result) sum += i;return sum;}
};
相关文章:

代码随想录算法训练营第三十五天|1005.K次取反后最大化的数组和 134. 加油站 135. 分发糖果
LeetCode 1005.K次取反后最大化的数组和 题目链接:1005.K次取反后最大化的数组和 踩坑:没有 思路:数组里有正有负,肯定先对负数进行取反,且从小开始。如果所有负数都为正后还可以取反,则如果此时次数为奇…...

鸿蒙开发HarmonyOS Next 网络框架retrofit 封装 viemodel使用
新手刚开始学习harmonyos开发,之前搞安卓开发习惯使用retrofit,结果在三方库中还真搜到了,然后就模拟学习一下。有不对的地方请指点一下。新手新手 oh-package.json5 引入库 retofit 需要使用2.0.1-rc.0 以上版本,修复了retrofit发送网络请…...
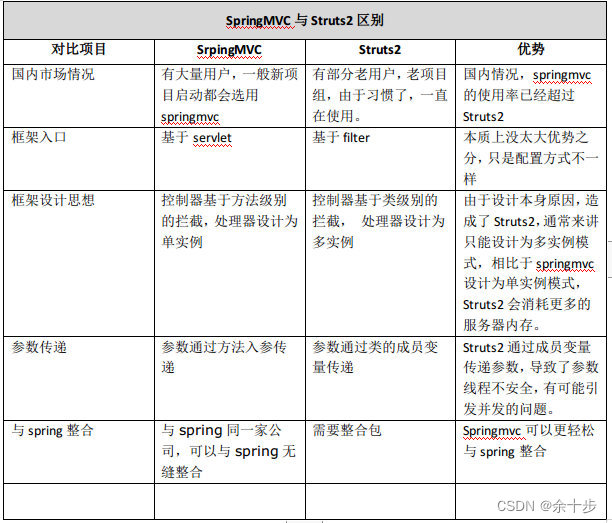
什么是SpringMVC
StringMvc简介 Spring web mvc和Struts2都属于表现层的框架,它是Spring框架的一部分,我们可以从Spring的整体结构中看得出来:...

【PowerDesigner】PDM生成建表脚本
目录 🌊1. PowerDesigner简介 🌍1.1 常用模型文件 🌍1.2 PowerDesigner使用环境 🌊2. PDM生成建表脚本 🌊3. 研究心得 🌊1. PowerDesigner简介 🌍1.1 常用模型文件 主要使用PowerDesigne…...
React实现在线预览word报告/本地选择报告预览
标题使用的核心技术点是docx-preview,读取到文件的File对象,用File去做文件展示,这里是才用将文件转base64字符串存储到localStorage中 在线预览word报告且包含word样式 下载需要使用的min.js文件进项目的public目录中(上zip已包…...

计算机哈佛架构、冯·诺依曼架构对比
哈佛架构和冯诺依曼架构是两种不同的计算机系统架构,它们在存储器组织方式上有着显著的区别。下面是它们的原理、优缺点的对比以及一些常见的 MCU 采用的架构: 哈佛架构: 原理:哈佛架构将指令存储器(程序存储器&#x…...

单片机串口发送为空中断和发送完成中断有什么区别?
单片机串口发送的空中断和发送完成中断在触发条件和功能上存在明显的区别。以下是关于这两种中断的详细解释: 【发送为空】中断(Transmit Data Register Empty Interrupt): 触发条件:当发送数据寄存器(TDR…...

css特效:对多个tag标签实现模拟地球仪特效
要实现对多个<a>标签(比如链接)的模拟地球仪特效和鼠标跟随特效,你可以使用CSS和一点点JavaScript来完成。下面是一个基本的示例代码:HTML代码: <!DOCTYPE html> <html lang"en"> <h…...

【2024Python教程】Python文件打包成exe,如果有图片怎么打包?有手就会的超简单教程
目录 pyinstaller模块打包exe(无图片或其他文件打包版) 第一步 安装pyinstaller模块: 第二步 找到需要打包的主程序文件夹 第三步 打包exe文件 第四步 确认exe文件是否可以打开 pyinstaller模块打包exe(有图片打包版--方法一…...
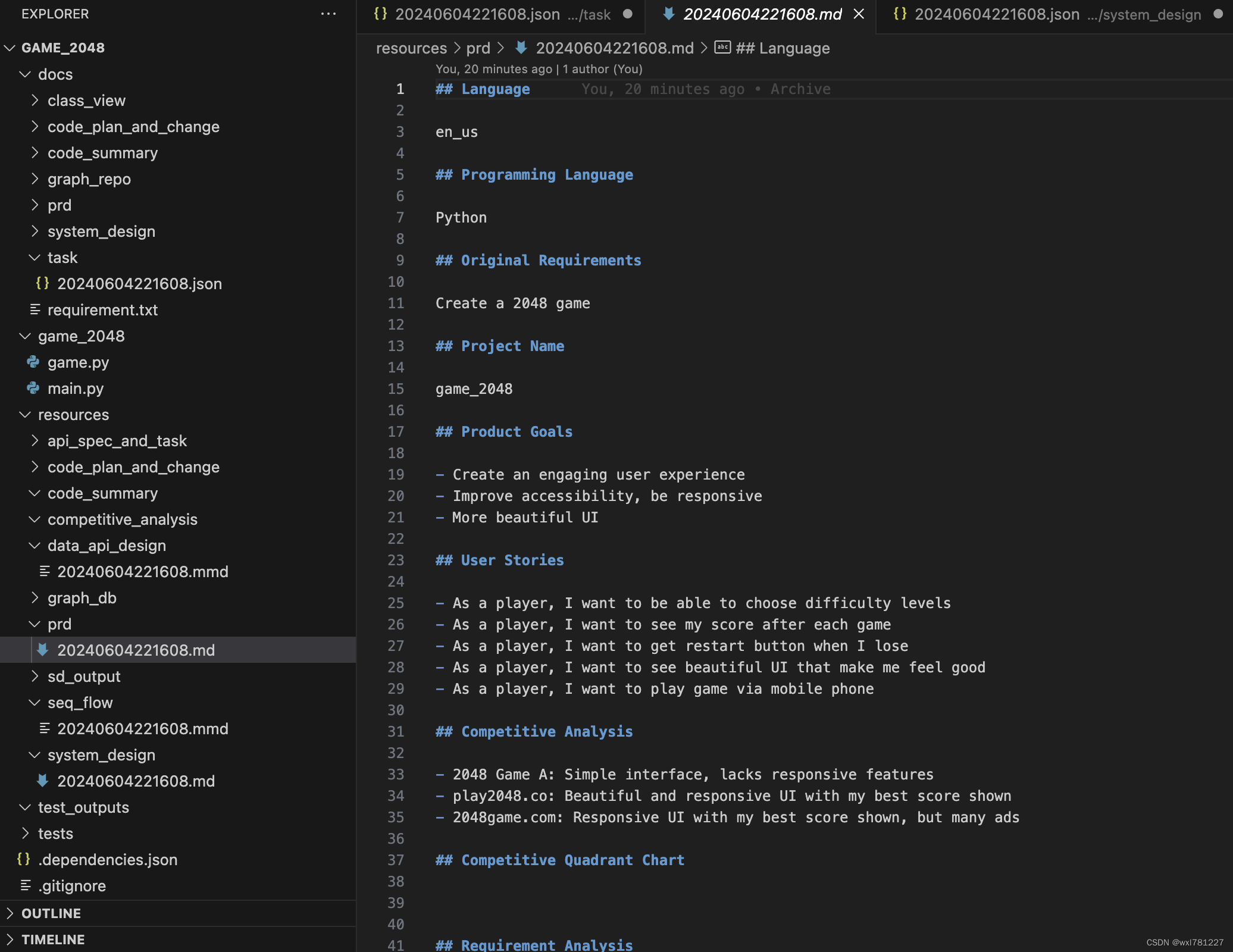
mac环境基于llama3和metaGPT自动开发2048游戏
1.准备虚拟环境 conda create -n metagpt python3.9 && conda activate metagpt 2.安装metagpt pip install --upgrade metagpt 3.初始化配置文件 metagpt --init-config 4. 安装llama3 5. 修改配置文件 6.让metegpt自动开发2048游戏 7.经过多轮迭代,最终…...

这些Linux知识可不是靠背就会的!
在信息技术日新月异的今天,Linux以其开源、稳定、高效的特性,逐渐成为了众多专业人士的首选操作系统。然而,关于Linux知识的学习,却常常陷入一个误区——许多人认为,掌握Linux就是死记硬背各种命令和参数。这种观念&am…...

openlayers 绘图功能,绘制多边形,draw组件的使用,一个简单的需求引发的思考(一)
1 需求 使用openlayers绘图功能绘制多边形 2 分析 主要是openlayers中draw功能的使用,感觉比较简单,祖传CV大法搞起来 3 实现 为了方便,就不加载底图了,直接使用绘制功能 2.1 简单实现 <template><div id"ma…...

【Flutter】 TextField限制长度时, 第三方手写输入法、ios原始拼音输入法输入被吞问题
问题描述 TextField限制长度时, 当你的输入字符长度已经到了最大值-1时,使用第三方手写输入法或者ios原生拼音输入法输入liang(什么拼音都行,这里只是举例),输到i那么li都会消失。 原因分析 这是因为第三…...

快递一键查询,只需快递单号,轻松掌握全程物流信息,让您的包裹追踪无忧!
在快节奏的现代生活中,快递已经成为我们生活中不可或缺的一部分。无论是网购的宝贝、亲朋好友寄来的礼物,还是工作中的紧急文件,快递都承载着我们的期待和需要。然而,面对众多的快递公司和复杂的查询流程,如何快速、准…...

【Java探索之旅】继承结构 继承和组合 protected final
文章目录 📑前言一、继承1.1 继承关系的代码块1.2 protected关键字1.3 继承方式1.4 final关键字1.5 继承与组合 🌤️全篇总结 📑前言 在面向对象编程中,继承是一种重要的概念,它允许我们创建一个新类,从现有…...

Ubuntu20.04-SLAM软件安装
目录 安装环境安装问题1.Ubuntu20.04在T440p上的安装问题1.1 安装后提示"x86/cpu:VMX(outside TXT) disabled by BIOS"1.2 ACPI Error:Needed type[Reference],found [Integer] 等错误1.3 ima: Error Communicating to TPM chip1.4 locate命令的安装 2.中文输入法-go…...

OSI七层网络参考模型
一、物理层 我们要发送出去的数据在计算机里只不过是无数的0和1,0或1就叫做比特,物理层就是把这些比特用不同的媒介传输出去,可以用电、光或者其他形式的电磁波来表示和传输信号,数据从网络接口出去以后,会经过不同的网…...
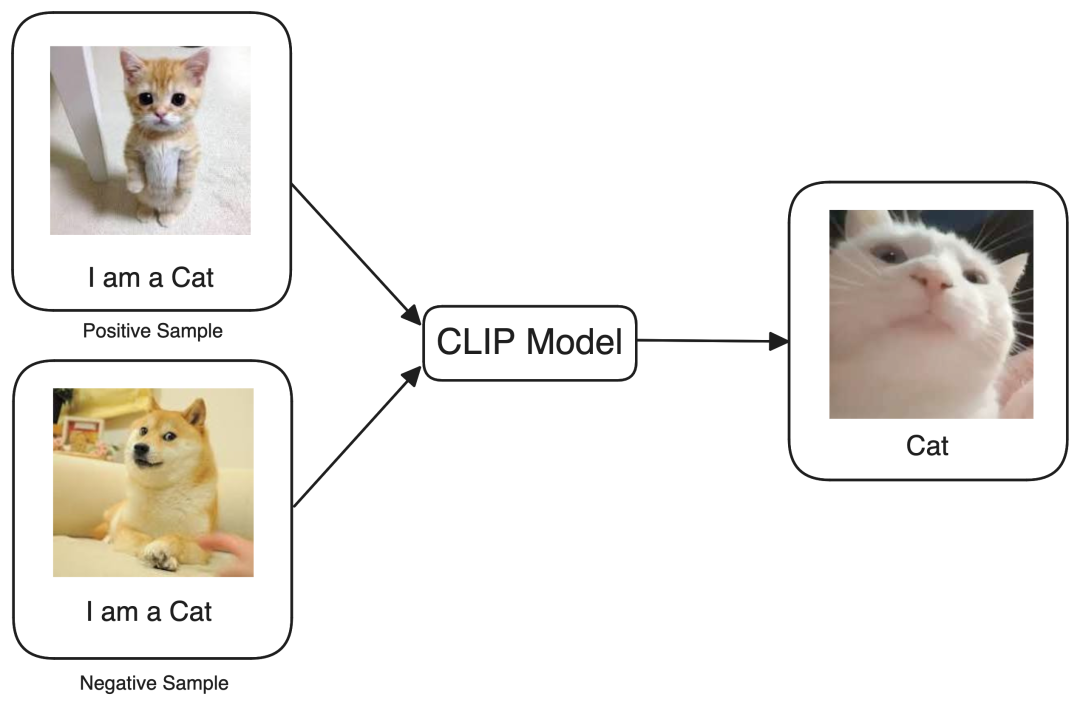
RAG与知识库搭建
Tip: 如果你在进行深度学习、自动驾驶、模型推理、微调或AI绘画出图等任务,并且需要GPU资源,可以考虑使用UCloud云计算旗下的Compshare的GPU算力云平台。他们提供高性价比的4090 GPU,按时收费每卡2.6元,月卡只需要1.7元每小时&…...
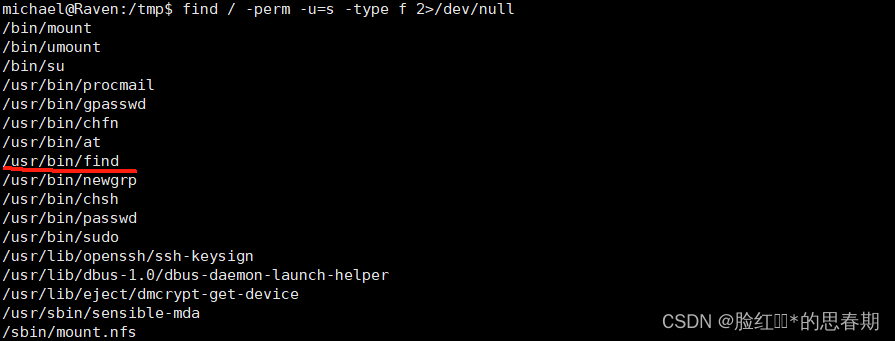
MySQL提权之UDF提权
1、前言 最近遇到udf提权,几经周折终于搞懂了。感觉挺有意思的,渗透思路一下子就被打开了。 2、什么是udf提权 udf 全称为user defined function,意思是用户自定义函数。用户可以对数据库所使用的函数进行一个扩展(windows利用…...

【设计模式】结构型设计模式之 组合模式
介绍 这里的组合模式,与之前的设计模式中的"组合关系"完全是两码事,这里的组合模式主要用来处理结构为树形的数据。 组合模式(Composite Pattern)是一种结构型设计模式,它允许你将对象组合成树状结构来表示…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

DingDing机器人群消息推送
文章目录 1 新建机器人2 API文档说明3 代码编写 1 新建机器人 点击群设置 下滑到群管理的机器人,点击进入 添加机器人 选择自定义Webhook服务 点击添加 设置安全设置,详见说明文档 成功后,记录Webhook 2 API文档说明 点击设置说明 查看自…...

Ubuntu Cursor升级成v1.0
0. 当前版本低 使用当前 Cursor v0.50时 GitHub Copilot Chat 打不开,快捷键也不好用,当看到 Cursor 升级后,还是蛮高兴的 1. 下载 Cursor 下载地址:https://www.cursor.com/cn/downloads 点击下载 Linux (x64) ,…...

macOS 终端智能代理检测
🧠 终端智能代理检测:自动判断是否需要设置代理访问 GitHub 在开发中,使用 GitHub 是非常常见的需求。但有时候我们会发现某些命令失败、插件无法更新,例如: fatal: unable to access https://github.com/ohmyzsh/oh…...
