二叉树从入门到AC(3)完全二叉树与堆
完全二叉树与堆
- 前言
- 优先队列:堆
- 向下调整维护堆
- 向上调整维护堆
- 堆的作用
前言
本文算是补充之前的系列,在前文中,讲了二叉树的基本结构与应用
二叉树从入门到AC(1)构建和前中后序遍历
二叉树从入门到AC(2)深度与层次遍历
二叉树的特殊形态
二叉树有两种常用的特殊形态:满二叉树和完全二叉树。如果一颗二叉树,其内部每个结点都有左右儿子,我们称之为满二叉树,这很好理解,如图所示:

我们在满二叉树中的最后一层,从右往左连续拔去至少零个结点,便是完全二叉树。也就是说,满二叉树是一种特殊的完全二叉树。

以上都为完全二叉树
那么如何判断一棵树是不是完全二叉树呢?我们可以运用层次遍历的结构(前文有代码),首先将储存一颗非空树,在队列中遵循:
1.如果遇到一个结点,左孩子为空,右孩子不为空,则该树一定不是完全二叉树
2.如果遇到一个结点,左孩子不为空,右孩子为空;或者左右孩子都为空,且则该节点之后的队列中的结点都为叶子节点,该树才是完全二叉树
3.以上两个一直都没触发,说明是满二叉树
优先队列:堆
堆,是一种特殊的完全二叉树,每个结点储存一个值,其中,若所有父结点都小于其子结点,称为最小堆,反之则是最大堆。如图:

二叉堆是一种基础数据结构,C++ 的STL中的优先队列就是使用二叉堆。另外,堆排序也是一种二叉堆算法。
堆的作用主要面向一个问题:如何高效的在一组数据中任意插入删除任何值的情况下,始终找到最小值/最大值。
这种数据结构也被称为优先队列。
向下调整维护堆
以上图的最小堆为例,在数组中按层次遍历储存为3,5,7,9,8,11
要求:不限次数的删除最小值并插入进新的值,保持堆的属性(最小值在堆顶)
这时候我们删除堆顶的最小值3,并且添加任意一个数如10到堆顶,只要能维护这个堆的属性,我们就可以得到新的最小值。
于是设计算法,我们从堆顶开始反复执行:把当前结点与左右儿子比对,并与最小的那个结点交换值,直到无法交换(要么是左右儿子都更大,要么是到叶子结点了)
如图所示:

于是我们维护住了一个最小堆,最大堆也是同理。那么在代码层就好写多了,我们可以根据数组下标发现,设当前结点下标为i,我们只需要每次与2i和2i+1相比并判断是否Swap就好

void Sswap(int a,int b)
{int c=0;c=arr[b];arr[b]=arr[a];arr[a]=c;
}
void siftdown(int i)//向下调整,用于寻找最值
{int t=0,flag=0;while(i*2<=n&&flag==0){if(arr[i]>arr[i*2])t=i*2;elset=i;if(t*2+1<=n){if(arr[t]>arr[i*2+1])t=i*2+1;}if(t!=i){Sswap(t,i);//交换两结点的值i=t;}elseflag=1;}
}
在主函数中,我们将数组调整为全局变量,并且i始终设为0,例如
int arr[6]={10,5,7,9,8,11};
int n=5;
int main()
{siftdown(0);for(int i=0;i<=n;i++){printf("%d ",arr[i]);}return 0;
}
执行结果:

向上调整维护堆
如果我们需要不断向堆中添加数值而不删除数值怎么办?那么我们可以从下面的叶子结点开始添加,并逐一往上比对,来维护堆。
void siftup(int i)
{int flag=0;if(i==0)return;while(i!=0&&flag==0){if(arr[i]<arr[i/2])Sswap(i,i/2);elseflag=1;i=i/2;}
}
我们将:arr[6]={3,5,7,9,8,1};
与i=5代入,

这便是堆的维护操作。
堆的作用
当我们输入一个数组,并求其最值时,我们一般会开max或min比对每个数并保留最值,这是时间复杂度最低的做法,为O(N)。但是当我们删除最小值并添加进一个新值之后,就相当于需要彻底进行一次重新排序,复杂度也来到了O(N^2),而同样的目的,由于堆的特性,维护起来只需要logN的时间。
那么我们如何用完全无序的数列建立一个堆呢?
void creat()
{int i=0;for(i=n/2;i>=0;i--){siftdown(i);}
}
即可。
在创建了堆之后,我们还有著名的排序方法,堆排序,网上到处都有模板在这里不赘述。另外,堆也是一种重要的优化思路出现在别的算法中,主旨都在于用更短的时间来在插入、删除元素的情况下捕捉最值(或者第n大的值也可以)。
相关文章:

二叉树从入门到AC(3)完全二叉树与堆
完全二叉树与堆 前言优先队列:堆向下调整维护堆向上调整维护堆堆的作用 前言 本文算是补充之前的系列,在前文中,讲了二叉树的基本结构与应用 二叉树从入门到AC(1)构建和前中后序遍历 二叉树从入门到AC(2&a…...
AI写作:如何让创作过程更流畅?
写作这件事一直让我们从小学生头痛到打工人,初高中时期800字的作文让我们焦头烂额,一篇作文里用尽了口水话,拼拼凑凑才勉强完成。 大学时期以为可以轻松顺利毕业,结果毕业前的最后一道坎拦住我们的是毕业论文,苦战几个…...

2024中国海洋装备展暨航海装备大会(福州海峡国际会展中心)
关于邀请参加2024中国海洋装备博览会的函 为加快推动海洋强国建设。在福建省人民政府的大力支持下,第二届中国海洋装备博览会将于2024年11月15-18日在福州举办。 博览会将进一步聚焦产业链和供应链协同创新,着力推动现代海洋产业体系建设,促进海洋科技…...

CyberDAO:引领Web3时代的DAO社区文化
致力于Web3研究和孵化 CyberDAO自成立以来,致力于推动Web3研究和孵化,吸引了来自技术、资本、商业、应用与流量等领域的上千名热忱成员。我们为社区提供多元的Web3产品和商业机会,触达行业核心,助力成员捕获Web3.0时代的红利。 目…...

测试面试点
在面试PC端测试人员时,你可以提出以下具体问题来深入了解候选人的技能、经验和思维方式: 1. 技术能力与基础知识 你能解释一下什么是黑盒测试和白盒测试吗?你在过去的工作中是如何应用这两种测试方法的? 答案:黑盒测…...

Nginx配置详细解释:(4)高级配置
目录 1.网页的状态页 2.Nginx第三方模块(echo) 3.变量 4.自定义访问日志 5.Nginx压缩功能 6.https功能 7.自定义图标 Nginx除了一些基本配置外,还有一些高级配置,如网页的状态,第三方模块需要另外安装,支持变量,…...

OceanBase 4.3 特性解析:列存技术
在涉及大规模数据的复杂分析或即时查询时,列式存储是支撑业务负载的关键技术之一。相较于传统的行式存储,列式存储采用了不同的数据文件组织方式,它将表中的数据以列为单位进行物理排列。这种存储模式允许在分析过程中,查询计算仅…...
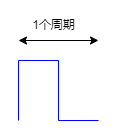
ARM32开发--PWM与通用定时器
知不足而奋进望远山而前行 目录 文章目录 前言 学习目标 学习内容 PWM pwm原理 需求 开发流程 初始化PWM PWM占空比控制 main函数修改duty 输出通道 关心的内容 重要的关键词 周期 分频 占空比 总结 前言 在微控制器开发中,理解和掌握PWM&#x…...
:栈帧(backtrace))
debugger(七):栈帧(backtrace)
〇、前言 在前面已经详细得介绍了栈帧,这里实现 backtrace。 一、backtrace 思路是遍历 stack,搜索 stack pointer,逐个打印栈帧信息,一直打印到 main 函数。 void Debugger::print_backtrace() {auto output_frame [frame_n…...
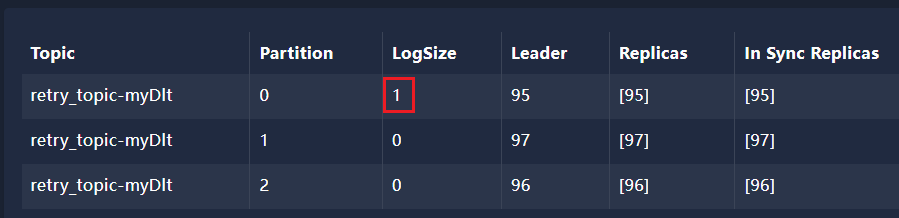
kafka-重试和死信主题(SpringBoot整合Kafka)
文章目录 1、重试和死信主题2、死信队列3、代码演示3.1、appication.yml3.2、引入spring-kafka依赖3.3、创建SpringBoot启动类3.4、创建生产者发送消息3.5、创建消费者消费消息 1、重试和死信主题 kafka默认支持重试和死信主题 重试主题:当消费者消费消息异常时&…...
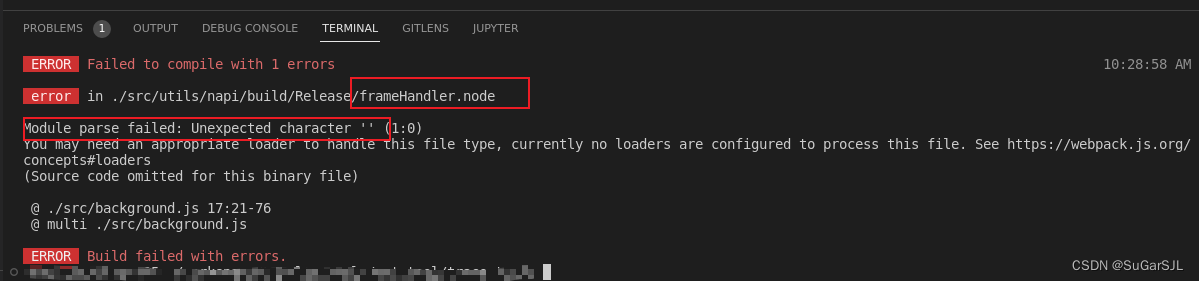
electron-Vue: Module parse failed: Unexpected character ‘ ‘
electron-Vue项目中,我自己写了一个node的C扩展(xx.node),然后在.vue文件里import它,然后运行npm run electron:serve,报错如下: electron-Vue打包默认使用webpack,默认情况下webpack没…...

贪心算法-数组跳跃游戏(mid)
目录 一、问题描述 二、解题思路 1.回溯法 2.贪心算法 三、代码实现 1.回溯法实现 2.贪心算法实现 四、刷题链接 一、问题描述 二、解题思路 1.回溯法 使用递归的方式,找到所有可能的走步方式,并记录递归深度(也就是走步次数&#x…...

C++经典150题
经典150题 数组/字符串 文章目录 经典150题数组/字符串88. 合并两个有序数组27.移除元素26.删除有序数组中的重复项80.删除有序数组重点重复项II169.多数元素189.轮转数组121.买卖股票的最佳时机123.买卖股票的最佳时机 III55.跳跃游戏45.跳跃游戏II 88. 合并两个有序数组 给…...

超详解——Python 序列详解——基础篇
目录 1. 序列的概念 字符串(String) 列表(List) 元组(Tuple) 2. 标准类型操作符 连接操作符() 重复操作符(*) 索引操作符([]) …...

DVWA-DC-6
靶机IP:192.168.20.140 kaliIP:192.168.20.128 网络有问题的可以看下搭建Vulnhub靶机网络问题(获取不到IP) 信息收集 nmap扫描靶机端口及版本信息 dirsearch扫目录 发现是个wordpress建站 我们去访问前端界面 存在重定向,修改hosts文件,加入192.168…...

ubuntu早期版本以及18.04后的版本,通过rc.local配置开机自启
在ubuntu早期版本以及18.04后的版本,还是支持在rc.local中进行操作开机自启。 1、编辑rc.local文件 cat <<EOF >/etc/rc.local #!/bin/sh -e # rc.local # This script is executed at the end of each multiuser runlevel. # Make sure that the script…...

【环境搭建】1.阿里云ECS服务器 安装jdk8
在阿里云服务器上安装 JDK 8 可以通过以下步骤完成。假设你使用的是 CentOS 或者其他基于 Red Hat 的发行版或Alibaba Cloud Linux 3.2104 LTS 64位。 1.更新系统软件包 sudo yum update -y2.安装 OpenJDK 8 使用 yum 包管理器安装 OpenJDK 8 sudo yum install -y java-1.8…...
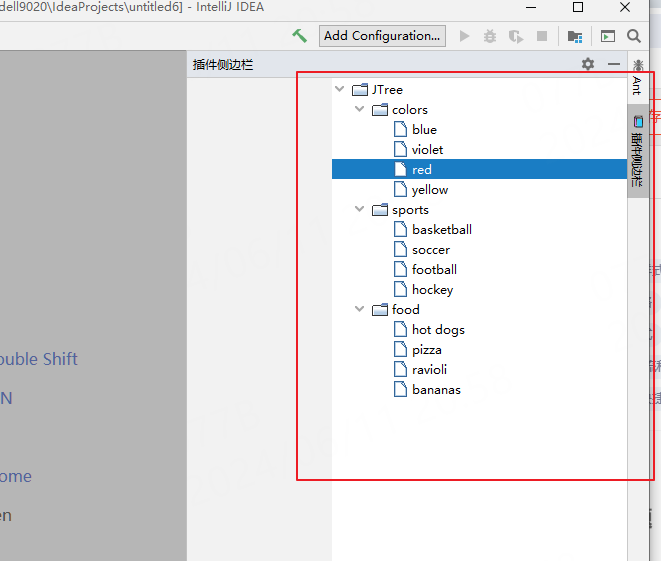
idea插件开发之定义侧边栏
写在前面 看下如何在侧边栏定义窗口,如下的效果: 1:正戏 先来定义UI,随便拖拽个组件,就看个效果: 接着定义一个工厂类来创建这个UI,需要实现接口com.intellij.openapi.wm.ToolWindowFactor…...

HarmonyOS未来五年的市场展望
一、引言 随着科技的不断进步和消费者对于智能化设备需求的日益增长,操作系统作为连接硬件与软件的核心平台,其重要性愈发凸显。HarmonyOS(鸿蒙系统),作为华为自主研发的分布式操作系统,自诞生以来便备受瞩…...
?)
R语言:什么是向量化操作(Vectorization)?
在R语言中,向量化操作是一个非常重要且强大的概念。它不仅提高了代码的简洁性和可读性,还大大提升了代码的执行效率。本文将详细介绍什么是向量化操作,并通过几个示例来展示其应用。 什么是向量化操作? 向量化操作是指在不使用显…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...

Web后端基础(基础知识)
BS架构:Browser/Server,浏览器/服务器架构模式。客户端只需要浏览器,应用程序的逻辑和数据都存储在服务端。 优点:维护方便缺点:体验一般 CS架构:Client/Server,客户端/服务器架构模式。需要单独…...

智能职业发展系统:AI驱动的职业规划平台技术解析
智能职业发展系统:AI驱动的职业规划平台技术解析 引言:数字时代的职业革命 在当今瞬息万变的就业市场中,传统的职业规划方法已无法满足个人和企业的需求。据统计,全球每年有超过2亿人面临职业转型困境,而企业也因此遭…...

负载均衡器》》LVS、Nginx、HAproxy 区别
虚拟主机 先4,后7...

PydanticAI快速入门示例
参考链接:https://ai.pydantic.dev/#why-use-pydanticai 示例代码 from pydantic_ai import Agent from pydantic_ai.models.openai import OpenAIModel from pydantic_ai.providers.openai import OpenAIProvider# 配置使用阿里云通义千问模型 model OpenAIMode…...

当下AI智能硬件方案浅谈
背景: 现在大模型出来以后,打破了常规的机械式的对话,人机对话变得更聪明一点。 对话用到的技术主要是实时音视频,简称为RTC。下游硬件厂商一般都不会去自己开发音视频技术,开发自己的大模型。商用方案多见为字节、百…...

Python异步编程:深入理解协程的原理与实践指南
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 持续学习,不断…...
