Java高阶数据结构-----并查集(详解)
目录
🧐一.并查集的基本概念&实例:
🤪二.并查集代码:
😂三:并查集的一些习题:
A.省份数量
B.等式方程的可满足性
🧐一.并查集的基本概念&实例:
并查集概念:将n个不同的元素划分成一些不相交的集合。开始时,每个元素自成一个单元素集合,然后按一定的规律将归于同一组元素的集合合并。在此过程中要反复用到查询某一个元素归属于那个集合的运算。适合于描述这类问题的抽象数据类型称为并查集(union-find set)。
有了上面的一定了解,我们再来看一个实例:
比如:某公司今年校招全国总共招生10人,西安招4人,成都招3人,武汉招3人,10个人来自不同的学校, 起先互不相识,每个学生都是一个独立的小团体,现给这些学生进行编号:{0, 1, 2, 3, 4, 5, 6, 7, 8, 9}; 给以下 数组用来存储该小集体,数组中的数字代表:该小集体中具有成员的个数。(负号下文解释)

毕业后,学生们要去公司上班,每个地方的学生自发组织成小分队一起上路,于是: 西安学生小分队s1={0,6,7,8},成都学生小分队s2={1,4,9},武汉学生小分队s3={2,3,5}就相互认识了,10个 人形成了三个小团体。假设右三个群主0,1,2担任队长,负责大家的出行。

一趟火车之旅后,每个小分队成员就互相熟悉,称为了一个朋友圈。

在公司工作一段时间后,西安小分队中8号同学与成都小分队1号同学奇迹般的走到了一起,两个小圈子的学生相互介绍,最后成为了一个小圈子:

现在0集合有7个人,2集合有3个人,总共两个朋友圈,负数的个数就是集合的个数
注意事项:
我们一般将数组中的元素初始化为-1
(数组的下标:) 数组的下标对应集合中元素的编号
(数组的值array[i]:) 数组中如果为负数,负号代表根,数字代表该集合中元素个数
(数组的值array[i]:)数组中如果为非负数,代表该元素双亲在数组中的下标
并查集能干的事:
-
查找元素属于哪个集合 沿着数组表示树形关系以上一直找到根(即:树中中元素为负数的位置)
-
查看两个元素是否属于同一个集合 沿着数组表示的树形关系往上一直找到树的根,如果根相同表明在同一个集合,否则不在
-
将两个集合归并成一个集合 将两个集合中的元素合并 将一个集合名称改成另一个集合的名称
🤪二.并查集代码:
import java.util.*;
public class UnionFindSet {public int[] elem;public UnionFindSet(int n){this.elem = new int[n];Arrays.fill(elem,-1);}//查询x的根节点,返回根节点的下标public int findRoot(int x){if(x < 0){throw new IndexOutOfBoundsException("下标不合法,是负数");}//一直等到数组里面的值为负数时,才找到一个根while(elem[x] >= 0){x = elem[x];}return x;}//查询x1和x2是否是同一个集合public boolean isSameUnionFindSet(int x1,int x2){int index1 = findRoot(x1);int index2 = findRoot(x2);if(index1 == index2) return true;return false;}//这是合并操作public void union(int x1,int x2){int index1 = findRoot(x1);int index2 = findRoot(x2);if(index1 == index2){return ;}elem[index1] = elem[index1] + elem[index2];elem[index2] = index1;}//查询集合的个数public int getCount(){int count = 0;for(int x : elem){if(x < 0) count++;}return count;}
}
那我们趁热打铁,来做两道题练习一下:
😂三:并查集的一些习题:
-
A.省份数量
- 题目链接:. - 力扣(LeetCode)
思路:我们初始化一个一维数组表示并查集(数组大小为城市的个数),遍历这个二维数组(isConnected[i][j] 表示 i , j 两个城市相连),用并查集将相连接的城市合并到一个集合中,最后统计集合中元素的个数,就是要求的省份个数
class Solution {//A.省份数量public int findCircleNum(int[][] isConnected) {int n = isConnected.length;UnionFindSet ufs = new UnionFindSet(n);//将连接在一起的城市合并for(int i = 0;i < isConnected.length;i++){for(int j = 0;j < isConnected[0].length;j++){if(isConnected[i][j] == 1){ufs.union(i,j);}}}//查找连接在一起的城市,即省份的个数,直接返回return ufs.getCount();}
}
/* 并查集的实现*/
class UnionFindSet {public int[] elem;public UnionFindSet(int n){this.elem = new int[n];Arrays.fill(elem,-1);}//查询x的根节点,返回根节点的下标public int findRoot(int x){if(x < 0){throw new IndexOutOfBoundsException("下标不合法,是负数");}while(elem[x] >= 0){x = elem[x];}return x;}//查询x1和x2是否是同一个集合public boolean isSameUnionFindSet(int x1,int x2){int index1 = findRoot(x1);int index2 = findRoot(x2);if(index1 == index2) return true;return false;}//这是合并操作public void union(int x1,int x2){int index1 = findRoot(x1);int index2 = findRoot(x2);if(index1 == index2){return ;}elem[index1] = elem[index1] + elem[index2];elem[index2] = index1;}//查询集合的个数public int getCount(){int count = 0;for(int x : elem){if(x < 0) count++;}return count;}}
运行结果:
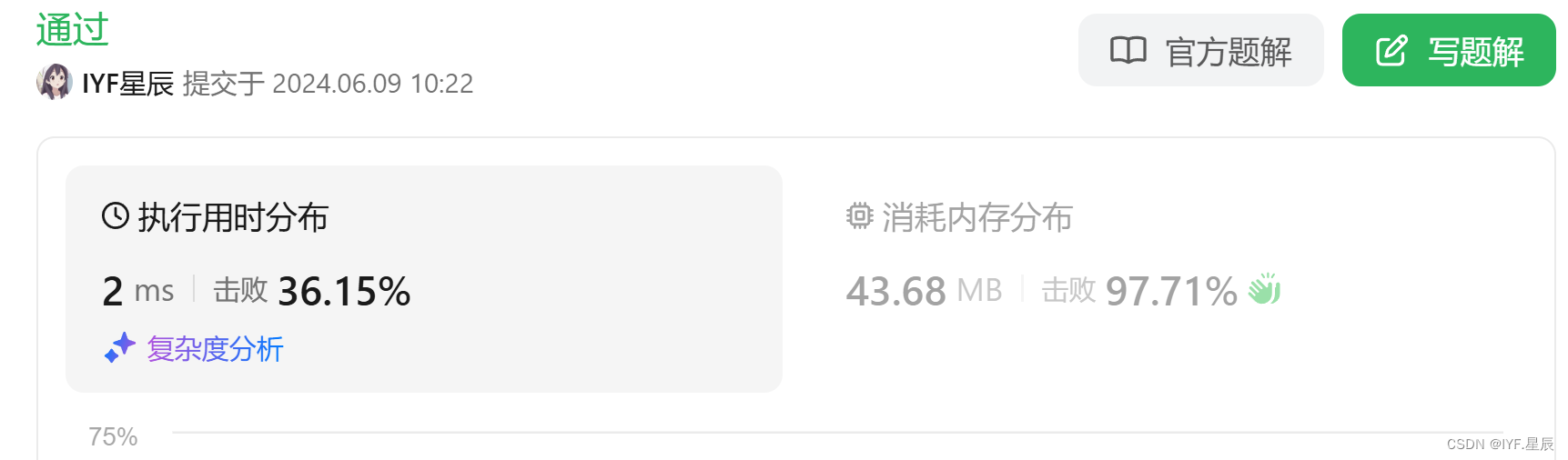
-
B.等式方程的可满足性
- 题目链接:. - 力扣(LeetCode)
思路:我们将具有相同属性的元素放入一个集合中,接着再遍历一遍字符串数组,如果字符串中对应的元素是!,说明不是一个集合,再从上述并查集中查找, 如果是一个集合的(矛盾了),返回false;遍历完成后也没有返回false,那么这个等式方程组就满足条件
class Solution {//B.等式方程的可满足性public boolean equationsPossible(String[] equations) {UnionFindSet ufs = new UnionFindSet(26);//将具有相同属性的元素放入一个集合中for(int i = 0;i < equations.length;i++){if(equations[i].charAt(1) == '='){ufs.union(equations[i].charAt(0) - 'a',equations[i].charAt(3) - 'a');}}//如果字符串中对应的元素是!,说明不是一个集合,再从上述并查集中查找, (矛盾了)如果是一个集合的,返回false;for(int i = 0;i < equations.length;i++){if(equations[i].charAt(1) == '!'){//查找根节点的下标位置int index1 = ufs.findRoot(equations[i].charAt(0) - 'a');int index2 = ufs.findRoot(equations[i].charAt(3) - 'a');if(index1 == index2) return false;}}return true;}
}
/* 并查集的实现 */
class UnionFindSet {public int[] elem;public UnionFindSet(int n){this.elem = new int[n];Arrays.fill(elem,-1);}//查询x的根节点,返回根节点的下标public int findRoot(int x){if(x < 0){throw new IndexOutOfBoundsException("下标不合法,是负数");}while(elem[x] >= 0){x = elem[x];}return x;}//查询x1和x2是否是同一个集合public boolean isSameUnionFindSet(int x1,int x2){int index1 = findRoot(x1);int index2 = findRoot(x2);if(index1 == index2) return true;return false;}//这是合并操作public void union(int x1,int x2){int index1 = findRoot(x1);int index2 = findRoot(x2);if(index1 == index2){return ;}elem[index1] = elem[index1] + elem[index2];elem[index2] = index1;}//查询集合的个数public int getCount(){int count = 0;for(int x : elem){if(x < 0) count++;}return count;}
}运行结果:
 结语: 写博客不仅仅是为了分享学习经历,同时这也有利于我巩固知识点,总结该知识点,由于作者水平有限,对文章有任何问题的还请指出,接受大家的批评,让我改进。同时也希望读者们不吝啬你们的点赞+收藏+关注,你们的鼓励是我创作的最大动力!
结语: 写博客不仅仅是为了分享学习经历,同时这也有利于我巩固知识点,总结该知识点,由于作者水平有限,对文章有任何问题的还请指出,接受大家的批评,让我改进。同时也希望读者们不吝啬你们的点赞+收藏+关注,你们的鼓励是我创作的最大动力!

相关文章:

Java高阶数据结构-----并查集(详解)
目录 🧐一.并查集的基本概念&实例: 🤪二.并查集代码: 😂三:并查集的一些习题: A.省份数量 B.等式方程的可满足性 🧐一.并查集的基本概念&实例: 并查集概念&…...
GitLab教程(三):多人合作场景下如何pull代码和处理冲突
文章目录 1.拉取别人同步的代码到本地的流程2.push冲突发生场景情景模拟简单的解决方法 在这一章中,为了模拟多人合作的场景,我需要一个人分饰两角。 执行git clone xx远端仓库地址 xx文件夹命令,在clone代码时指定本地仓库的文件夹名&#…...

模版偏特化之std::enable_if
1 SFINAE。 2 条件特化。可用作额外的函数参数(不可应用于运算符重载)、返回类型(不可应用于构造函数与析构函数),或类模板或函数模板形参。 函数参数: #include <iostream> #include <type_tra…...

好用的Web数据库管理工具推荐(ChatGPT的推荐)
在现代数据管理和开发中,Web数据库管理工具变得越来越重要。这些工具不仅提供了直观的用户界面,还支持跨平台操作,方便用户在任何地方进行数据库管理。 目录 1. SQLynx 2. phpMyAdmin 3. Adminer 4. DBeaver 5 结论 以下是几款推荐的Web…...
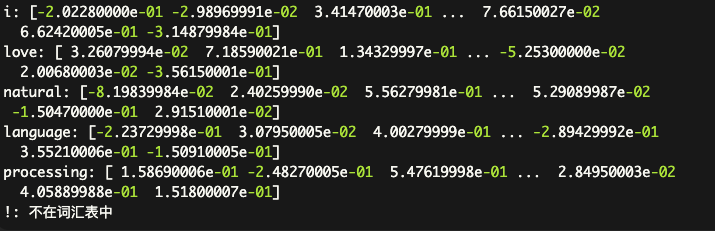
encoding Token和embedding 傻傻分不清楚?
encoding 编码 “encoding” 是一个在计算机科学和人工智能领域广泛使用的术语,它可以指代多种不同的过程和方法。核心就是编码:用某些数字来表示特定的信息。当然你或许会说字符集(Unicode)更理解这种概念,编码更强调这种动态的过程。而字符…...
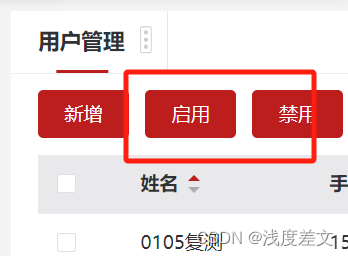
一个公用的数据状态修改组件
灵感来自于一项重复的工作,下图中,这类禁用启用、审核通过不通过、设计成是什么状态否什么状态的场景很多。每一个都需要单独提供接口。重复工作还蛮大的。于是,基于该组件类捕获组件跳转写了这款通用接口。省时省力。 代码如下:…...

[python]yfinance国内不能使用
yfinance国内不能使用,可以使用tushare、akshare代替 import yfinance as yf# 输入股票代码 stock_symbol AAPL # 替换为你想要查询的股票代码# 获取股票数据 data yf.download(stock_symbol)# 打印实时数据 print(data) pip install akshare import akshare …...
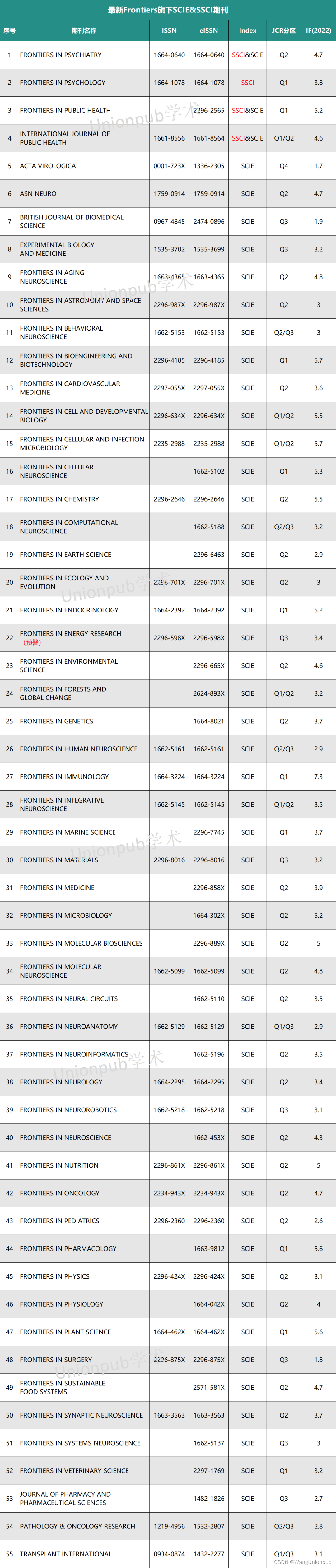
Frontiers旗下期刊,23年分区表整理出炉!它还值得投吗?
本周投稿推荐 SSCI • 中科院2区,6.0-7.0(录用友好) EI • 各领域沾边均可(2天录用) CNKI • 7天录用-检索(急录友好) SCI&EI • 4区生物医学类,0.5-1.0(录用…...

基于JSP的毕业生就业信息管理系统
开头语: 你好,我是专注于信息系统开发的学长猫哥。如果您对毕业生就业信息管理或相关技术感兴趣,欢迎联系我交流。 开发语言: JSP 数据库: MySQL 技术: JSP技术 SSM框架 工具: Eclips…...

CDN、CNAME、DNS
CDN、CNAME、DNS 域名解析是将域名转换为IP地址的过程。当用户在浏览器中输入域名时,计算机需要在DNS系统中找到对应的IP地址,以便能够访问该网站。 CDN(Content Delivery Network,内容分发网络)是一种用于加速网站访…...

直播商城源码-PC+APP+H5+小程序现成源码
随着电商行业的不断演进,直播商城已成为连接消费者和商品的新兴桥梁。直播商城源码提供了一个完整的解决方案,使得企业能够迅速搭建起一个覆盖PC、APP、H5和小程序的全渠道电商平台。本文将探讨直播商城源码的优势、关键功能以及如何选择适合的现成源码。…...

16. 《C语言》——【牛客网BC124 —— BC130题目讲解】
亲爱的读者,大家好!我是一名正在学习编程的高校生。在这个博客里,我将和大家一起探讨编程技巧、分享实用工具,并交流学习心得。希望通过我的博客,你能学到有用的知识,提高自己的技能,成为一名优…...

Docker 国内镜像源更换
实现 替换docker 镜像源 前提要求 安装 docker docker-compose 参考创建一键更换docker国内镜像源 Docker 镜像代理DaoCloud 镜像站百度云 https://mirror.baidubce.com南京大学镜像站...

python07
__init__.py from . import p1 from . import p2 # 理解:import p2 先导入 p2 文件, 然后该文件的内容全要 from . # # 告诉调用者,哪些文件需要使用 p1.py def sum(a,b):print(a b) p2.py def max(a,b):if a > b:print(a)else:pri…...
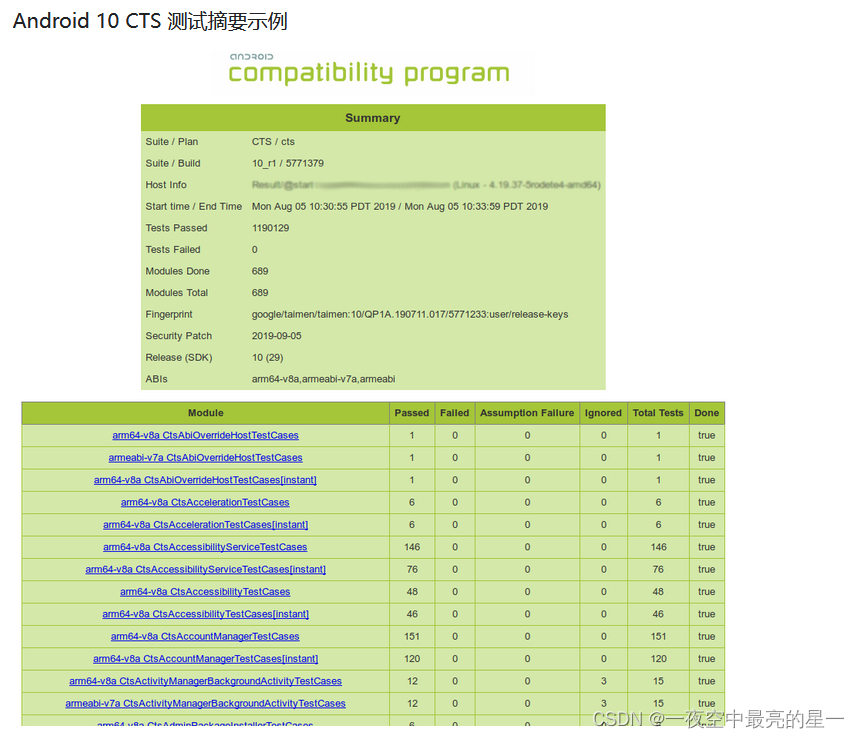
【CTS】android CTS测试
android CTS测试 1.硬件准备2. 软件准备3. 下载 CTS3.1 cts3.2 解压 CTS 包: 4 配置adb fastboot5 检查 Java 版本6 安装aapt26.1 下载并安装 Android SDK6.2 找到 aapt2 工具6.3 配置环境变量 7. 准备测试设备8. 运行 CTS 测试8.1 启动 CTS: 9. 查看测试…...
【雷丰阳-谷粒商城 】【分布式基础篇-全栈开发篇】【08】【商品服务】Object划分_批量删除
持续学习&持续更新中… 守破离 【雷丰阳-谷粒商城 】【分布式基础篇-全栈开发篇】【08】【商品服务】Object划分_批量删除 Object划分批量删除/添加参考 Object划分 数据库中对于一张表的数据,由于拥有隐私字段、多余字段、字段过少等原因,不应该直…...
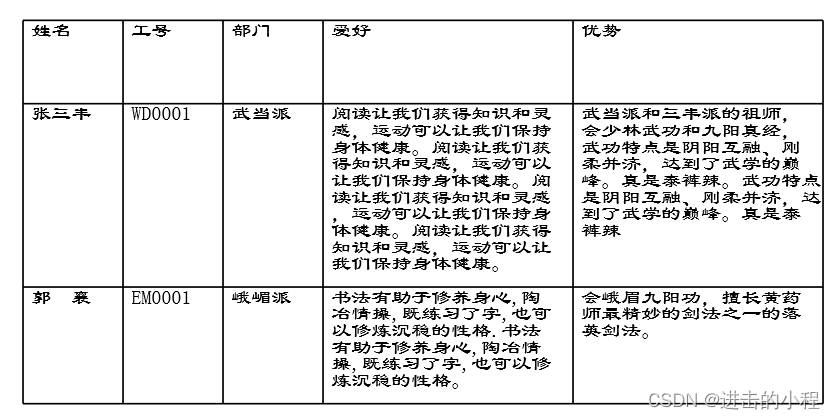
JAVA开发 PDF文件生成表格,表格根据内容自动调整高度
1、展示效果 2、相关功能实现 JAVA开发 使用Apache PDFBox库生成PDF文件,绘制表格 3、实现代码 import org.apache.pdfbox.pdmodel.PDDocument; import org.apache.pdfbox.pdmodel.PDPage; import org.apache.pdfbox.pdmodel.PDPageContentStream; import org.ap…...

OSINT技术情报精选·2024年6月第1周
OSINT技术情报精选2024年6月第1周 2024.6.11版权声明:本文为博主chszs的原创文章,未经博主允许不得转载。 1、经合组织:《2024数字经济展望:第1卷,拥抱技术前沿》 经合组织近日发布《2024数字经济展望》报告第一卷,…...

惊艳的短视频:成都科成博通文化传媒公司
惊艳的短视频:瞬间之美,震撼心灵 在数字化时代,短视频以其短小精悍、内容丰富的特点,迅速占领了我们的屏幕和时间。而在这个浩如烟海的视频海洋中,总有一些短视频能够脱颖而出,以其惊艳的视觉效果、深刻的…...

消费增值模式引领业绩飙升与用户活跃
大家好,我是吴军,致力于为您揭示私域电商领域的独特魅力与机遇。 今日,我很高兴与大家分享一个激动人心的成功案例。我们的客户在短短一个月的时间里,业绩就飙升至上百万级别,其用户活跃度更是居高不下,日…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...
