代码随想录-Day29
491. 非递减子序列
给你一个整数数组 nums ,找出并返回所有该数组中不同的递增子序列,递增子序列中 至少有两个元素 。你可以按 任意顺序 返回答案。
数组中可能含有重复元素,如出现两个整数相等,也可以视作递增序列的一种特殊情况。
示例 1:
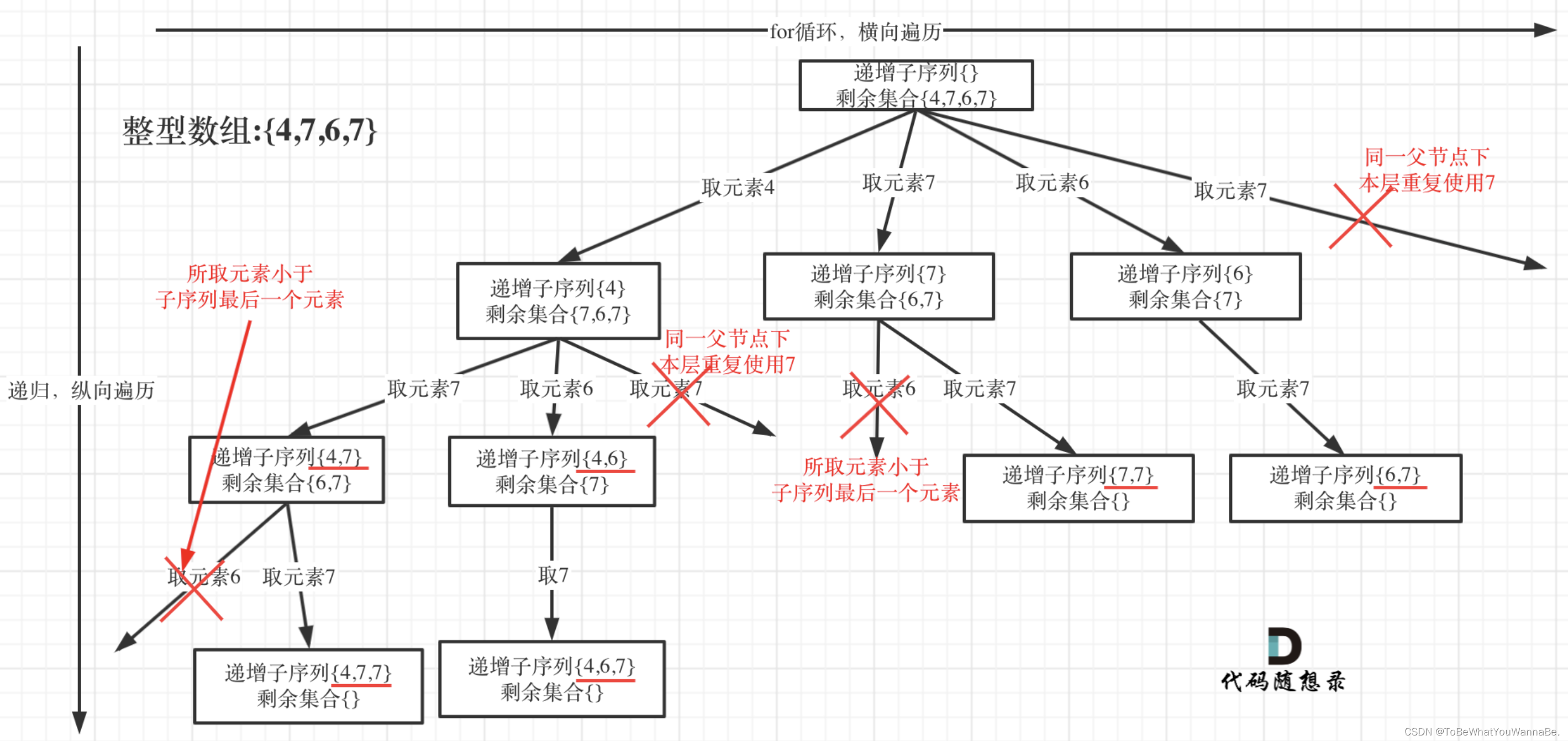
输入:nums = [4,6,7,7]
输出:[[4,6],[4,6,7],[4,6,7,7],[4,7],[4,7,7],[6,7],[6,7,7],[7,7]]
示例 2:
输入:nums = [4,4,3,2,1]
输出:[[4,4]]
class Solution {private List<Integer> path = new ArrayList<>();private List<List<Integer>> res = new ArrayList<>();public List<List<Integer>> findSubsequences(int[] nums) {backtracking(nums,0);return res;}private void backtracking (int[] nums, int start) {if (path.size() > 1) {res.add(new ArrayList<>(path));}int[] used = new int[201];for (int i = start; i < nums.length; i++) {if (!path.isEmpty() && nums[i] < path.get(path.size() - 1) ||(used[nums[i] + 100] == 1)) continue;used[nums[i] + 100] = 1;path.add(nums[i]);backtracking(nums, i + 1);path.remove(path.size() - 1);}}
}
这段代码定义了一个名为Solution的类,该类包含方法用于寻找给定整数数组nums中所有递增的非空子序列。递增子序列是指数组中数字按顺序排列(每个数字可以重复)的子集。以下是代码的详细解析:
类成员变量
path: 一个List<Integer>类型的变量,用于存储当前递归路径上的数字,即当前正在构建的递增子序列。res: 另一个List<List<Integer>>类型的变量,用于存储所有找到的递增子序列。
方法 findSubsequences
- 功能: 接收一个整型数组
nums作为输入,返回该数组的所有递增非空子序列。 - 实现: 首先调用
backtracking方法启动回溯过程,并返回最终结果列表res。
方法 backtracking
- 输入参数:
nums: 整型数组,全局输入数据。start: 整型变量,表示当前回溯搜索的起始位置,避免重复使用已经确定不在子序列中的元素。
- 功能: 通过回溯算法递归地构建所有递增子序列。
回溯核心逻辑
-
剪枝: 如果当前路径
path的大小超过1(意味着至少有两个元素),说明找到了一个有效的递增子序列,将其添加到结果列表res中。 -
避免重复: 引入一个整型数组
used来标记当前层递归中nums[i]是否已经被使用过,以避免生成重复子序列。数组大小为201,是因为整数范围为-100到100,通过加100映射到数组索引中,这样可以使用正数索引,简化判断和访问逻辑。 -
遍历与选择: 从
start位置开始遍历nums数组,对于每个元素,执行以下操作:- 如果当前路径非空且新元素小于路径尾部元素,或者当前元素在当前层已使用过(由
used数组判断),则跳过此次循环继续下一个元素,这是为了保证子序列递增且不重复。 - 标记当前元素在当前层已使用。
- 将当前元素加入路径
path。 - 以当前位置的下一个元素为起点,进行下一层递归调用。
- 回溯:从路径中移除最后一个元素,恢复到上一步状态,尝试下一个可能的选择。
- 如果当前路径非空且新元素小于路径尾部元素,或者当前元素在当前层已使用过(由
最终,当回溯过程完成,所有递增子序列会被收集在res中,并由findSubsequences方法返回。
46. 全排列
给定一个不含重复数字的数组 nums ,返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。
示例 1:
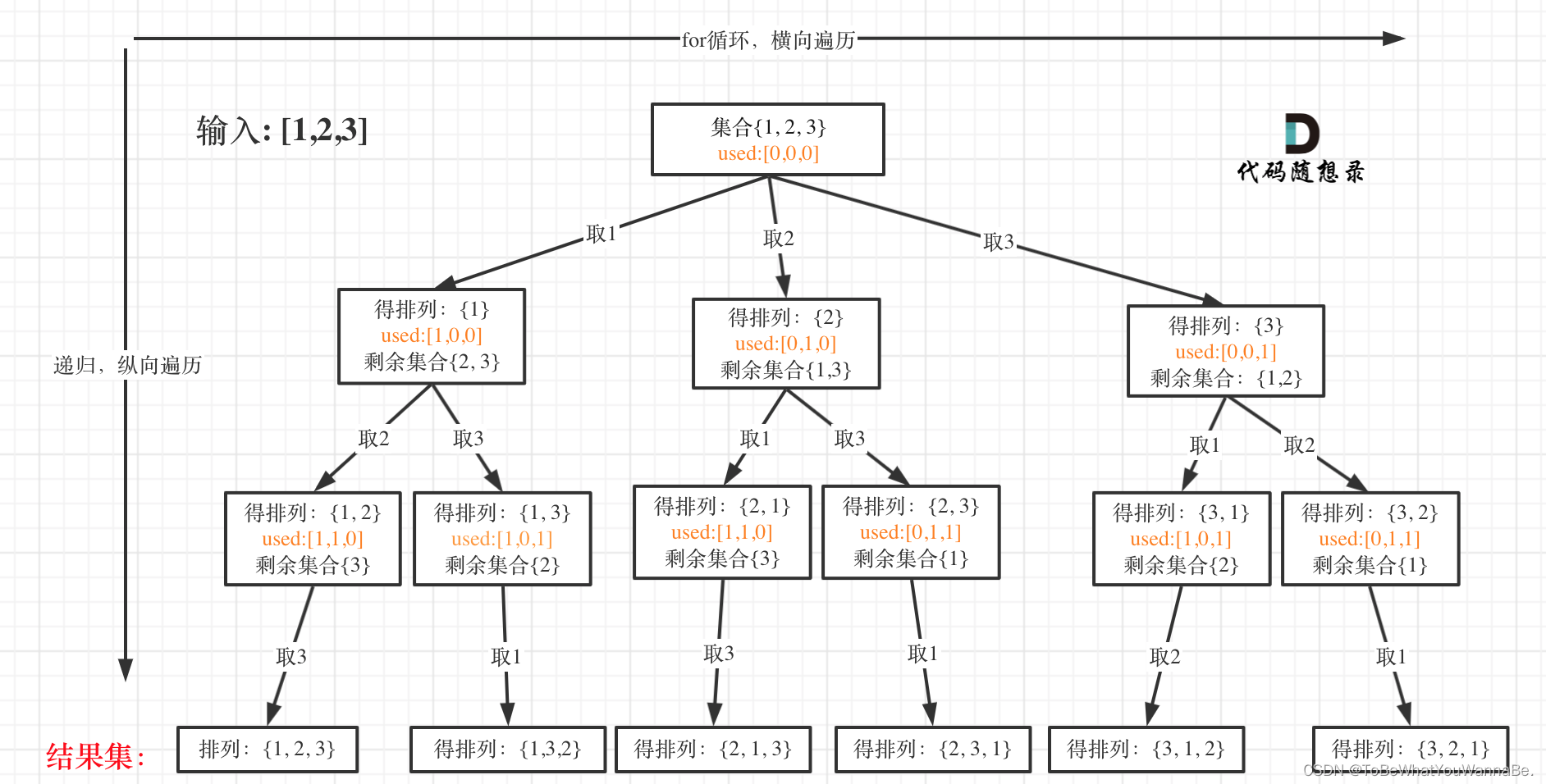
输入:nums = [1,2,3]
输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
示例 2:
输入:nums = [0,1]
输出:[[0,1],[1,0]]
示例 3:
输入:nums = [1]
输出:[[1]]
class Solution {List<List<Integer>> result = new ArrayList<>();// 存放符合条件结果的集合LinkedList<Integer> path = new LinkedList<>();// 用来存放符合条件结果boolean[] used;public List<List<Integer>> permute(int[] nums) {if (nums.length == 0){return result;}used = new boolean[nums.length];permuteHelper(nums);return result;}private void permuteHelper(int[] nums){if (path.size() == nums.length){result.add(new ArrayList<>(path));return;}for (int i = 0; i < nums.length; i++){if (used[i]){continue;}used[i] = true;path.add(nums[i]);permuteHelper(nums);path.removeLast();used[i] = false;}}
}
这段代码定义了一个名为Solution的类,其中主要实现了获取一个整型数组所有可能的排列组合的功能。下面是详细的解析:
类成员变量
result: 类型为List<List<Integer>>,用于存储所有满足条件的排列结果。path: 类型为LinkedList<Integer>,作为一个临时列表,用于在递归过程中暂存当前排列。used: 类型为boolean[],标记数组中的元素在当前排列中是否已被使用过,避免重复选择。
方法 permute
- 功能: 接收一个整型数组
nums作为输入,返回该数组所有可能的排列组合。 - 逻辑:
- 首先检查输入数组是否为空,若为空直接返回空结果列表。
- 初始化布尔数组
used,长度与输入数组相同,用于记录每个元素的使用状态。 - 调用辅助函数
permuteHelper(nums)来进行实际的排列生成。
方法 permuteHelper
- 功能: 实现深度优先搜索(DFS)回溯算法来生成所有排列。
- 逻辑:
- 当
path的大小等于原数组长度时,说明已经生成了一个完整的排列,将其添加到结果列表result中,然后返回。 - 对于数组
nums中的每个元素,进行以下操作:- 若该元素已经在当前排列中使用过(
used[i] == true),则跳过,避免重复。 - 标记该元素为已使用(
used[i] = true),将它添加到path中。 - 递归调用
permuteHelper(nums)生成剩余元素的排列。 - 在递归调用返回后(即处理完以当前元素为固定位置的所有情况),需要“撤销”选择:将
used[i]重置为false,并将nums[i]从path中移除,回溯到上一层继续尝试其他元素。
- 若该元素已经在当前排列中使用过(
- 当
综上所述,这个程序利用回溯算法深度优先遍历所有可能的排列组合情况,有效地解决了给定数组元素的全排列问题。
相关文章:

代码随想录-Day29
491. 非递减子序列 给你一个整数数组 nums ,找出并返回所有该数组中不同的递增子序列,递增子序列中 至少有两个元素 。你可以按 任意顺序 返回答案。 数组中可能含有重复元素,如出现两个整数相等,也可以视作递增序列的一种特殊情…...
C/C++ 进阶(6)红黑树
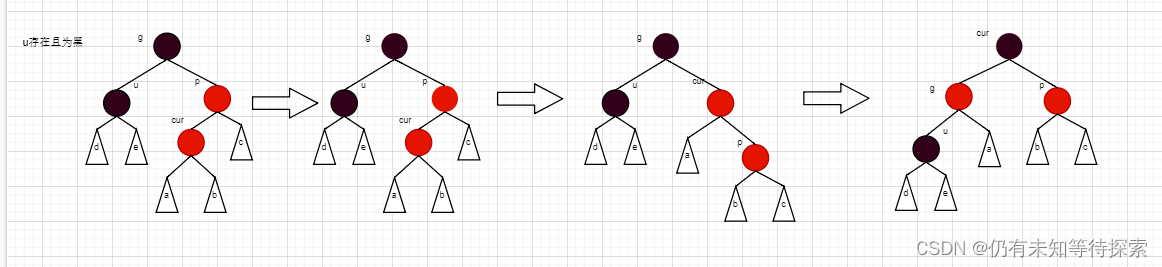
个人主页:仍有未知等待探索-CSDN博客 专题分栏:C 目录 一、概念 性质 二、操作 插入 情况一:cur为红、p为红、g为黑,如果u存在且为红 步骤: 情况二:cur为红、p为红、g为黑,如果u不存在或…...

【Vue】构建vuex-cart模块
说明:既然明确数据要存 vuex,建议分模块存,购物车数据存 cart 模块,将来还会有 user 模块,article 模块… 新建 store/modules/cart.js 挂载到 vuex 仓库上 store/cart.js import Vue from vue import Vuex from vu…...

如何成为嵌入式系统工程师?
各位朋友,如果你们有意向投身于嵌入式开发领域,那么强烈建议你们在软件和硬件两个方面均展开深入且全面的学习。 嵌入式计算机作为嵌入式系统的核心技术支撑,其是直接面向用户、产品以及应用的,无论是软件还是硬件方面都能发挥重要…...

【AI大模型】Transformers大模型库(七):单机多卡推理之device_map
目录 一、引言 二、单机多卡推理之device_map 2.1 概述 2.2 自动配置,如device_map"auto" 2.3 手动配置,如device_map"cuda:1" 三、总结 一、引言 这里的Transformers指的是huggingface开发的大模型库&#x…...

驱动代码编写(一)
驱动程序的作用 驱动程序是指与硬件设备和操作系统进行通信的软件。它的主要功能有以下几个方面: 提供硬件支持:驱动程序允许操作系统与硬件设备进行通信,以便正确地操作和控制硬件设备。它可以向操作系统提供有关硬件设备的各种信息&#x…...

Prompt-to-Prompt Image Editing with Cross Attention Control
Prompt-to-Prompt Image Editing with Cross Attention Control (P2P) Amir Hertz, Tel Aviv University, ICLR23, Paper, Code 1. 前言 编辑对这些生成模型来说是具有挑战性的,因为编辑技术的一个固有特性是保留大部分原始图像,而在基于文本的模型中…...

实验11 OSPF协议配置
实验11 OSPF协议配置 一、OSPF单区域配置(一)原理描述(二)实验目的(三)实验内容(四)实验配置(五)实验步骤 二、OSPF多区域配置(一)原理…...
ChatGPT-4o, 腾讯元宝,通义千问对比测试中文文化
国内的大模型应用我选择了国内综合实力最强的两个,一个是腾讯元宝,一个是通义千问。其它的豆包,Kimi,文心一言等在某些领域也有强于竞品的表现。 问一个中文文化比较基础的问题,我满以为中文文化chatGPT不如国内的大模型。可事实…...

node.js学习
node.js学习实操及笔记 温故node.js,node.js学习实操过程及笔记~ node.js学习视频node.js官网node.js中文网实操笔记githubcsdn笔记 为什么学node.js 可以让别人访问我们编写的网页为后续的框架学习打下基础,三大框架vue react angular离不开node.js …...

python将一个图片雕刻镂空成二维码
本文使用创作助手。 要将一个图片雕刻镂空成二维码,你可以使用Python中的Pillow库来处理图像,并使用qrcode库来生成二维码。以下是一个示例代码,用于将图片雕刻镂空成二维码: import qrcode from PIL import Image# 打开待处理的…...
OS进程取样器OS Process Sampler执行CMD/Shell命令
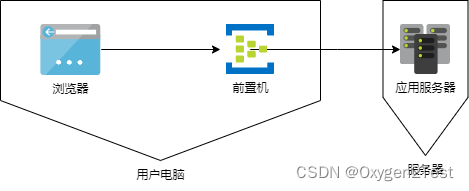
Apache JMeter - Users Manual: Component Reference 1.背景 项目上最近需要测试一种很少用到的DICOM协议,但是网上资料很少,基本上可以总结为三种方案: 直接发送TCP 16进制数据包,但是参数化数据准备难度大通过开发封装jar包发送,需要开发组提供通过发送cmd命令给前置机…...

excel两个数据表格,怎样实现筛选的联动?
如图,想要通过处理器或者像素条件进行筛选,形成一个右边图2的对比表,如何实现实现联动显示呢? 这个在excel里可以借用数据透视表切片器来完成。步骤如下: 1.添加表 选中数据区域中任意一个单元格,点击 插…...

python,django好的get和post请求
获得get请求 df request.GET.get("dades")获得post请求 文件settings.py关闭csrf MIDDLEWARE [ ‘django.middleware.security.SecurityMiddleware’, ‘django.contrib.sessions.middleware.SessionMiddleware’, ‘django.middleware.common.CommonMiddleware’…...

volatile的用法
目录 前言 使用volatile的注意事项: 示例: 总结: 前言 在嵌入式C编程中,volatile是一个关键字,它用于告知编译器被修饰的变量可能会在程序的任何地方、任何时候被不可预见的、非程序本身控制的因素所改变。这通常…...

MySQL 与 PostgreSQL 关键对比二(SQL语法)
目录 1 详细示例 1.1自动增量列 1.2 字符串连接 1.3 JSON 支持 2 总结 MySQL 和 PostgreSQL 是两种流行的开源关系数据库管理系统(RDBMS)。尽管它们在许多方面相似,但在 SQL 语法和功能上存在一些显著差异。 以下SQL语句的执行如果需要开…...

徐州服务器租用该如何维护?
服务器能够帮助企业处理网络上大部分的数据和信息,在互联网行业中起着十分重要的作用,服务器的存在能够保障网站稳定的运行,主要是由内存、硬盘和处理器等组成,服务器除了进行正常的工作运行,还需要定期维护和管理&…...
—— 栈)
C++习题精选(4)—— 栈
目录 1. 最小栈2. 栈的压入弹出序列3. 逆波兰表达式求值 1. 最小栈 题目描述:设计一个支持 push ,pop ,top 操作,并能在常数时间内检索到最小元素的栈。实现 MinStack 类: MinStack() 初始化堆栈对象。 void push(int val) 将元素…...
)
Web前端ES6-ES13笔记合集(下)
#### 五.ES10新特性 ##### 1. Object.fromEntries > Object.fromEntries()方法允许你轻松地将键值对列表转换为对象 js const arr [["name", "kerwin"], ["age", 100]]; console.log(Object.fromEntries(arr))//{name: kerwin, age: 100} …...

我要成为算法高手-双指针篇
目录 什么是双指针?问题1:移动零问题2:复写零问题3:快乐数问题4:盛最多水的容器问题5:有效三角形个数问题6:查找总价格和为目标值的两个商品(两数之和)问题7:三数之和问题8:四数之和…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...

AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...

LabVIEW双光子成像系统技术
双光子成像技术的核心特性 双光子成像通过双低能量光子协同激发机制,展现出显著的技术优势: 深层组织穿透能力:适用于活体组织深度成像 高分辨率观测性能:满足微观结构的精细研究需求 低光毒性特点:减少对样本的损伤…...

手机平板能效生态设计指令EU 2023/1670标准解读
手机平板能效生态设计指令EU 2023/1670标准解读 以下是针对欧盟《手机和平板电脑生态设计法规》(EU) 2023/1670 的核心解读,综合法规核心要求、最新修正及企业合规要点: 一、法规背景与目标 生效与强制时间 发布于2023年8月31日(OJ公报&…...
)
LLaMA-Factory 微调 Qwen2-VL 进行人脸情感识别(二)
在上一篇文章中,我们详细介绍了如何使用LLaMA-Factory框架对Qwen2-VL大模型进行微调,以实现人脸情感识别的功能。本篇文章将聚焦于微调完成后,如何调用这个模型进行人脸情感识别的具体代码实现,包括详细的步骤和注释。 模型调用步骤 环境准备:确保安装了必要的Python库。…...
