Pytorch 实现简单的 线性回归 算法
Pytorch实现简单的线性回归算法
简单 tensor的运算
Pytorch涉及的基本数据类型是tensor(张量)和Autograd(自动微分变量)
import torch
x = torch.rand(5, 3) #产生一个5*3的tensor,在 [0,1) 之间随机取值
y = torch.ones(5, 3) #产生一个5*3的Tensor,元素都是1 z = x + y #两个tensor可以直接相加
q = x.mm(y.transpose(0, 1)) #x乘以y的转置 mm为矩阵的乘法,矩阵相乘必须某一个矩阵的行与另一个矩阵的列相等
Tensor与numpy.ndarray之间的转换
import numpy as np #导入numpy包
a = np.ones([5, 3]) #建立一个5*3全是1的二维数组(矩阵)
b = torch.from_numpy(a) #利用from_numpy将其转换为tensor
c = torch.FloatTensor(a) #另外一种转换为tensor的方法,类型为FloatTensor,还可以使LongTensor,整型数据类型
b.numpy() #从一个tensor转化为numpy的多维数组
from torch.autograd import Variable # 导入自动梯度的运算包,主要用Variable这个类
x = Variable(torch.ones(2, 2), requires_grad=True) # 创建一个Variable,包裹了一个2*2张量,将需要计算梯度属性置为True
用pytorch做一个简单的线性关系预测
线性关系是一种非常简单的变量之间的关系,因变量和自变量在线性关系的情况下,可以使用线性回归算法对一个或多个因变量和自变量间的线性关系进行建模,该模型的系数可以用最小二乘法进行求解。生活中的场景往往会比较复杂,需要考虑多元线性关系和非线性关系,用其他的回归分析方法求解。
x = Variable(torch.linspace(0, 100, 100).type(torch.FloatTensor)) # 生成一些样本点作为原始数据
rand = Variable(torch.randn(100)) * 10 # 随机生成100个满足标准正态分布的随机数,均值为0,方差为1.将这个数字乘以10,标准方差变为10
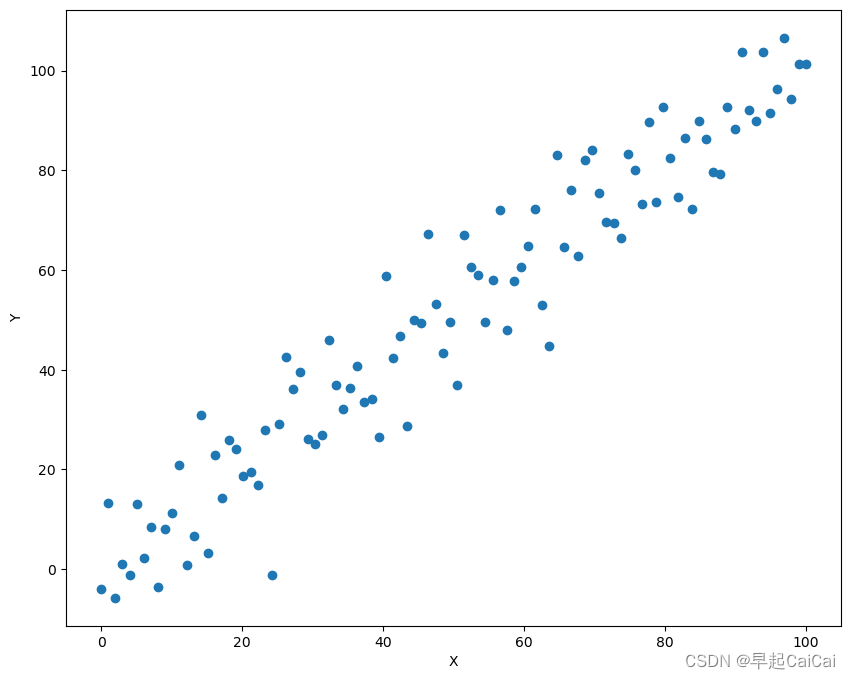
y = x + rand # 将x和rand相加,得到伪造的标签数据y。所以(x,y)应能近似地落在y=x这条直线上import matplotlib.pyplot as plt
plt.figure(figsize=(10,8)) #设定绘制窗口大小为10*8 inch
plt.plot(x.data.numpy(), y.data.numpy(), 'o') #绘制数据,考虑到x和y都是Variable,需要用data获取它们包裹的Tensor,并专成numpy
plt.xlabel('X')
plt.ylabel('Y')
plt.show()
构建模型
#a,b就是要构建的线性函数的系数
a = Variable(torch.rand(1), requires_grad = True) #创建a变量,并随机赋值初始化
b = Variable(torch.rand(1), requires_grad = True) #创建b变量,并随机赋值初始化
print('Initial parameters:', [a, b])learning_rate = 0.0001 #设置学习率
for i in range(1000):### 增加了这部分代码,清空存储在变量a,b中的梯度信息,以免在backward的过程中会反复不停地累加if (a.grad is not None) and (b.grad is not None): a.grad.data.zero_() b.grad.data.zero_() predictions = a.expand_as(x) * x+ b.expand_as(x) #计算在当前a、b条件下的模型预测数值# 在 PyTorch 中,a.expand_as(x) 用于将张量 a 扩展(expand)为与张量 x 具有相同的形状loss = torch.mean((predictions - y) ** 2) #通过与标签数据y比较,计算误差print('loss:', loss)loss.backward() #对损失函数进行梯度反传,backward的方向传播算法a.data.add_(- learning_rate * a.grad.data) #利用上一步计算中得到的a的梯度信息更新a中的data数值b.data.add_(- learning_rate * b.grad.data) #利用上一步计算中得到的b的梯度信息更新b中的data数值绘制结果
x_data = x.data.numpy() # 将tensor 转为 numpy
plt.figure(figsize = (10, 7))
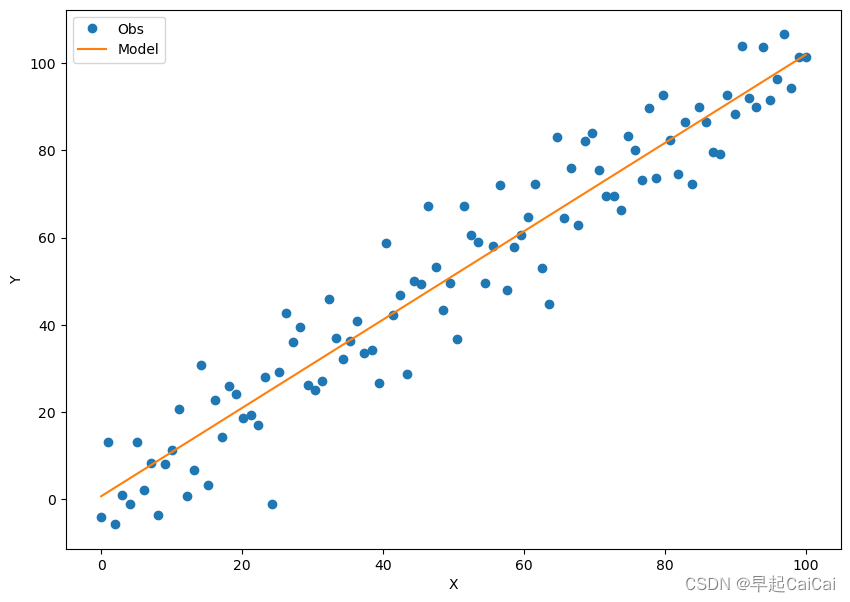
xplot = plt.plot(x_data, y.data.numpy(), 'o') # 绘制原始数据
yplot = plt.plot(x_data, a.data.numpy() * x_data + b.data.numpy()) #绘制拟合数据
plt.xlabel('X')
plt.ylabel('Y')
str1 = str(a.data.numpy()[0]) + 'x +' + str(b.data.numpy()[0]) # 图例信息 拟合的直线
plt.legend(['Obs', 'Model']) #绘制图例
plt.show()
x_test = Variable(torch.FloatTensor([1, 2, 10, 100, 1000])) #随便选择一些点1,2,……,1000
predictions = a.expand_as(x_test) * x_test + b.expand_as(x_test) #计算模型的预测结果
predictions #输出预测的数值
相关文章:

Pytorch 实现简单的 线性回归 算法
Pytorch实现简单的线性回归算法 简单 tensor的运算 Pytorch涉及的基本数据类型是tensor(张量)和Autograd(自动微分变量) import torch x torch.rand(5, 3) #产生一个5*3的tensor,在 [0,1) 之间随机取值 y torch.o…...
Django中配置日志
在Django中配置日志的方法非常简单,只需要在 setting 文件中添加配置项,系统会自动生成相应的日志文件,也可以配置调试时显示内容,报错发送邮件等操作。 在setting.py中添加以下配置。 # 日志配置 LOGS_DIRS os.path.join(BASE…...

海外盲盒小程序背后的技术支撑与实现
海外盲盒小程序之所以能够迅速崛起并受到全球消费者的喜爱,除了其独特的商业模式和营销策略外,更重要的是其背后的技术支撑和实现。本文将深入探讨海外盲盒小程序背后的技术支撑及其实现方式。 一、多语言与本地化技术 为了满足全球不同地区消费者的需…...

vue问题记录
vue3 路由跳转携带参数 路由跳转携带参数 query方法 //跳转传参 this.$router.push({path:/home,query: {id:1}}) //接受参数 this.$route.query.id问题:刷新页面,参数会丢失—未解决 将参数存在本地存储中,但是组件销毁时,清…...
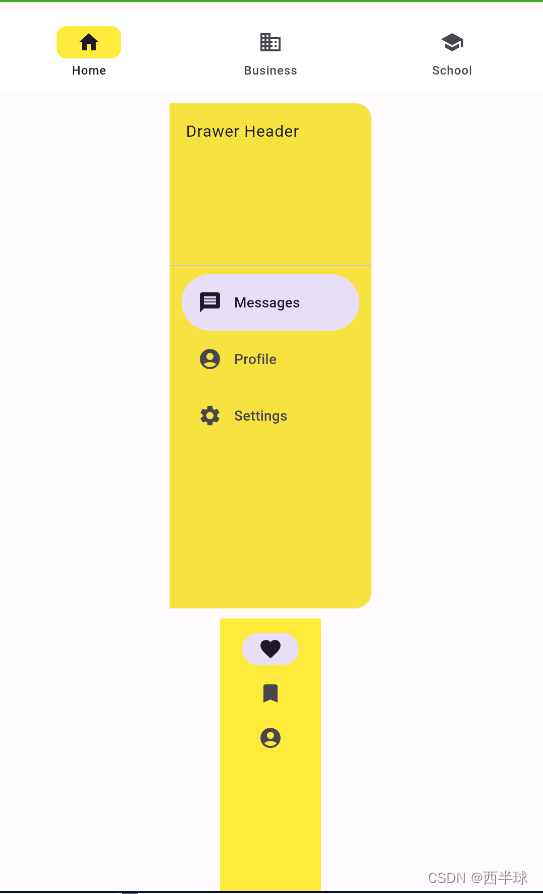
Flutter - Material3适配
demo 地址: https://github.com/iotjin/jh_flutter_demo 代码不定时更新,请前往github查看最新代码 Flutter - Material3适配 对比图具体实现一些组件的变化 代码实现Material2的ThemeDataMaterial3的ThemeData Material3适配官方文档 flutter SDK升级到3.16.0之后 …...

一个有趣的c++案例
1. 源码 #include <stdio.h> #include <stdint.h> #include <iostream>using namespace std;uint8_t a 0; uint8_t b 0;#define MY_LOG#ifdef MY_LOG#define my_log(...) printf(__VA_ARGS__); fflush(stdout)#else #define my_log(...) #endifvoid …...

【python】OpenCV—Background Estimation(15)
文章目录 中值滤波中值滤波得到图像背景移动侦测 学习来自 OpenCV基础(14)OpenCV在视频中的简单背景估计 中值滤波 中值滤波是一种非线性平滑技术,主要用于数字信号处理,特别是在图像处理中去除噪声。 一、定义与原理 定义&am…...
【Java毕业设计】基于JavaWeb的旅游论坛管理系统
文章目录 摘 要目 录1 概述1.1 研究背景及意义1.2 国内外研究现状1.3 拟研究内容1.4 系统开发技术1.4.1 Java编程语言1.4.2 vue技术1.4.3 MySQL数据库1.4.4 B/S结构1.4.5 Spring Boot框架 2 系统需求分析2.1 可行性分析2.2 系统流程2.2.1 操作流程2.2.2 登录流程2.2.3 删除信息…...

讲一下v-model的底层实现原理?
什么是v-model? 在Vue.js中,v-model是一个用于实现双向数据绑定的指令。它通常用于表单控件上,以便能够在视图和数据模型之间自动同步数据。具体来说,当用户在输入框中输入内容时,数据模型会自动更新;当数…...

大模型基础——从零实现一个Transformer(3)
大模型基础——从零实现一个Transformer(1)-CSDN博客 一、前言 之前两篇文章已经讲了Transformer的Embedding,Tokenizer,Attention,Position Encoding, 本文我们继续了解Transformer中剩下的其他组件. 二、归一化 2.1 Layer Normalization layerNorm是针对序列数据提出的一种…...

一二三应用开发平台应用开发示例——概述、应用开发示例简介及创建前后端模块
概述 对于应用开发平台的核心基石——系统管理模块,我精心撰写了一份详尽的说明手册。该手册旨在从使用者的角度出发,不仅全面阐述系统的各项属性和功能,更着重强调使用过程中的注意事项和最佳实践。 在手册的编写过程中,我特别…...

springboot+minio+kkfileview实现文件的在线预览
在原来的文章中已经讲述过springbootminio的开发过程,这里不做讲述。 原文章地址: https://blog.csdn.net/qq_39990869/article/details/131598884?spm1001.2014.3001.5501 如果你的项目只是需要在线预览图片或者视频那么可以使用minio自己的预览地址进…...

HTML5+CSS3小实例:粘性文字的滚动效果
实例:粘性文字的滚动效果 技术栈:HTML+CSS 效果: 源码: 【HTML】 <!DOCTYPE html> <html lang="zh-CN"><head><meta charset="UTF-8"><meta name="viewport" content="width=device-width, initial-sca…...

Java 关于抽象 -- Java 语言的抽象类、接口和函数式接口
大家好,我是栗筝i,这篇文章是我的 “栗筝i 的 Java 技术栈” 专栏的第 008 篇文章,在 “栗筝i 的 Java 技术栈” 这个专栏中我会持续为大家更新 Java 技术相关全套技术栈内容。专栏的主要目标是已经有一定 Java 开发经验,并希望进一步完善自己对整个 Java 技术体系来充实自…...

用 Notepad++ 写 Java 程序
安装包 百度网盘 提取码:6666 安装步骤 双击安装包开始安装。 安装完成: 配置编码 用 NotePad 写 Java 程序时,需要设置编码。 在 设置,首选项,新建 中进行设置,可以对每一个新建的文件起作用。 Note…...

malloc brk mmap
malloc 是一个库函数,通常在 C 标准库中实现,用于动态内存分配。malloc 的具体实现可能因库、操作系统和平台而异,但通常它会与底层操作系统提供的内存管理功能进行交互。 对于大多数现代操作系统(如 Unix、Linux、Windows 等&am…...

java多线程相关概念
在Java多线程编程中,有几个关键的术语需要理解: 1.线程(Thread):线程是操作系统能够进行运算调度的最小单位,它被包含在进程之中,是进程中的实际运作单位。 2.进程(Process):进程是系统进行资源分配和调度…...

【html】简单网页模板源码
大家每一次在写网页的时候会不会因为布局而困扰今天就给大家带来一个我自己亲自编写的网页的基本的模板大家可以直接去利用,大家也可以利用自己的想法去做空间的美化和完善。 源码: html: <!DOCTYPE html> <html lang"zh"><…...
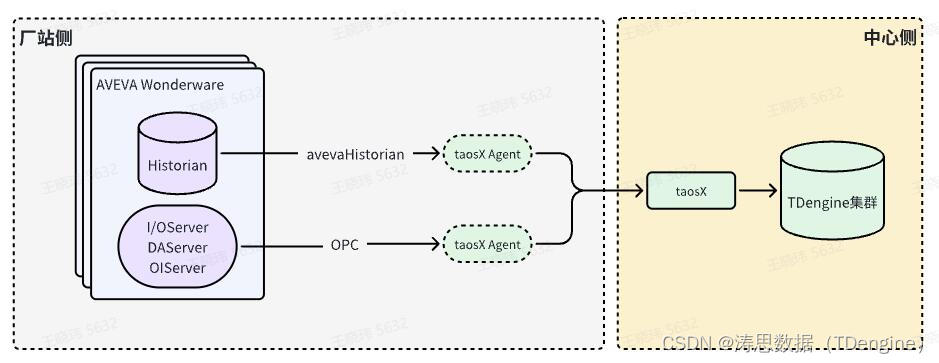
借助Historian Connector + TDengine,打造工业创新底座
在工业自动化的领域中,数据的采集、存储和分析是实现高效决策和操作的基石。AVEVA Historian (原 Wonderware Historian) 作为领先的工业实时数据库,专注于收集和存储高保真度的历史工艺数据。与此同时,TDengine 作为一款专为时序数据打造的高…...

51单片机-实机演示(LED点阵)
目录 前言: 一.线位置 二.扩展 三.总结 前言: 这是一篇关于51单片机实机LED点阵的插线图和代码说明.另外还有一篇我写的仿真的连接在这:http://t.csdnimg.cn/ZNLCl,欢迎大家的点赞,评论,关注. 一.线位置 接线实机图. 引脚位置注意: 1. *-* P00->RE8 P01->RE7 …...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...
