C语言王国——数据的内存管理
目录
一、引言
二、整形在内存中的存储
2.1 进制之间的转换
2.1.1 整形的二进制
2.1.2 十进制和二进制
2.1.3 十进制和八进制的转换
2.1.4 十六进制和十进制的转换
2.2 原码,反码,和补码
三、大、小端字节序
3.1 大小端的定义
3.2 为什么会有大小端之分
3.3 代码区分
四、浮点型在内存中的存储
五、结论
一、引言
众所周知,计算机只能识别二进制语言,原理在于计算机只能识别打开和关闭的电信号,也就是0和1。那么我们日常生活中各种负载的数据计算机是怎么识别和存储的呢。作为一个高端的程序员,我们不仅仅要会写代码,也要去了解计算机的运行原理和存储方式,所以接下来,姜糖将会给大家阐述一下我学习到的关于数据的内存管理的相关知识。
二、整形在内存中的存储
整数是我们日常生活中常见的数据类型,所以我们先来讲讲整数。
2.1 进制之间的转换
2.1.1 整形的二进制
由sizeof(int)得知,整形有4个字节,而4个字节由32个bit构成,在计算机科学中,1位(bit)是最小的计算机存储单位,可以存储一个二进制的数值,即0或1。
所以整形的二进制是:如图,图中方格表示位,里面是0或者1。

当整形为0时,32个位全为0,加2则如图:
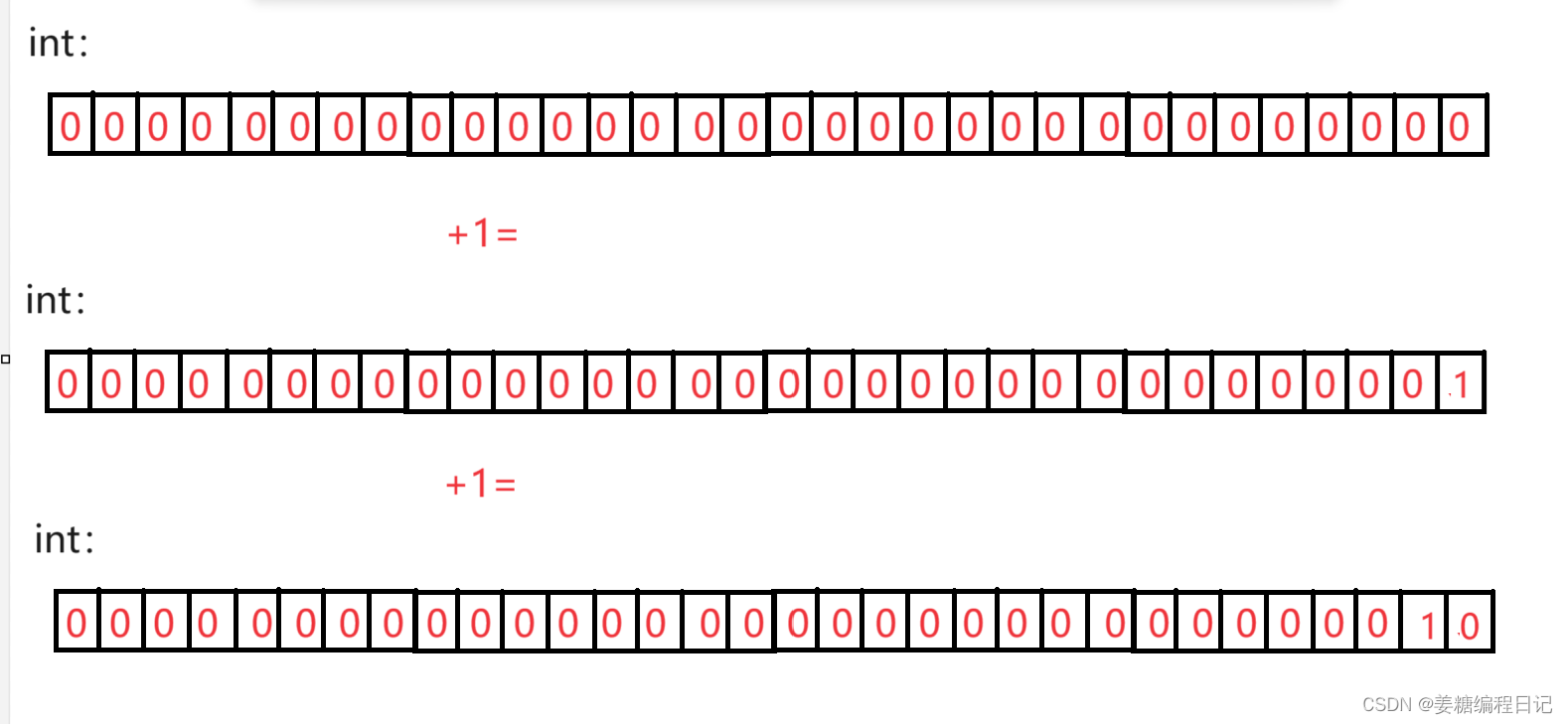
因为计算机只能识别0和1所以当计算机遇到2时就会进一位,如十进制遇十进位一样。
而我们在计算机里常用的就是二进制,八进制和十六进制,生活中我们一般用十进制,所以接下来姜糖就来给大家讲一下它们的转换。
2.1.2 十进制和二进制
首先是我们最常见最熟悉的十进制。它们之间怎么转换呢?
我们再次观察二进制的结构会发现如图的规律:

当前方格中的数*2^(方格从右往前数的个数-1) = 当前方格在十进制中的表示
然后将它们加起来就行了,如图中第一位为1,在十进制中表示1,其他方格为0,0*任何数字为0,所以就是0+1=1,所以十进制也为1。
2.1.3 十进制和八进制的转换
那么八进制怎么转换为八进制呢?
而转换为十进制的方法而和二进制大同小异:
当前方格中的数*8^(所在位数-1) = 当前方格在十进制中的表示
2.1.4 十六进制和十进制的转换
那么十六进制有该如何转换呢?
由前面可知,十六进制也只包含0~15的数字,那么在存两位数的时候会和一位数搞混,如存15时,那1和5怎么办。所以十六进制中10~15用a~f表示。
那么先转换成二进制,我们发现4个二进制位可以完美放下0~15的数字,所以4个二进制位表示一个十六进制的位:

当前方格中的数*16^(方格从右往前数的个数-1) = 当前方格在十进制中的表示
2.2 原码,反码,和补码
正数中,原码,反码,补码都相同。
在我们生活中不仅有正数还有负数的存在,那么负数在计算机里又是怎么存储的呢?
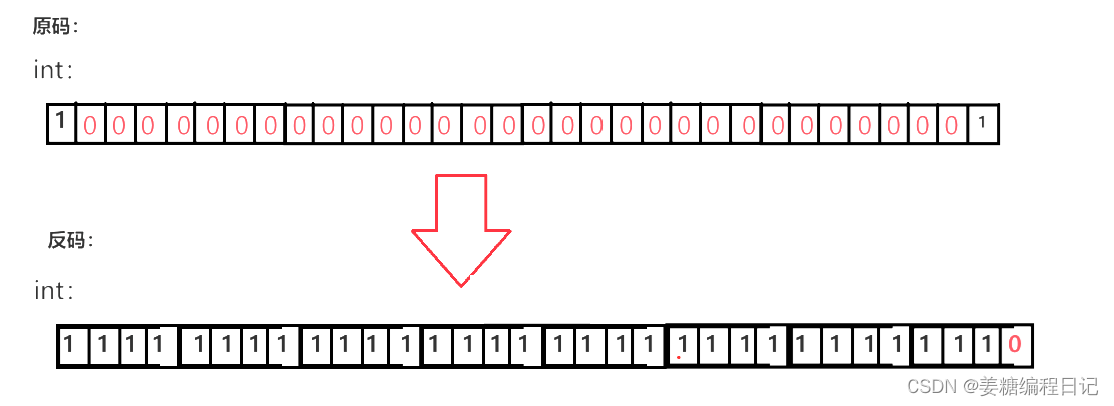
计算机规定把数值位最高的一位当作字符位,0为正,1为负:如图位:+1

我刚刚跟大家讲的就是数据的原码,而反码就是将原码的符号位不变,其他位依次按位取反就可以得到反码,则0变成1,1变成0
补码则为反码+1:
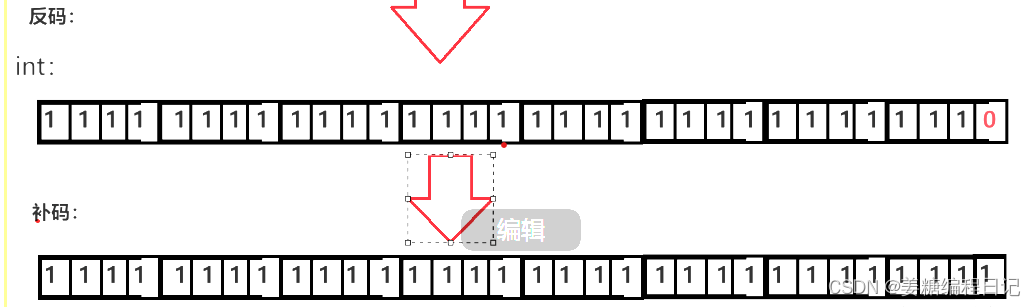
*补码变成原码,不用倒推,符号位不变,取反+1便可
而我们在计算机中一般存放的是补码,你这是为什么呢?
在计算机系统中,数值⼀律⽤补码来表⽰和存储。 原因在于,使⽤补码,可以将符号位和数值域统⼀处理; 同时,加法和减法也可以统⼀处理(CPU只有加法器)此外,补码与原码相互转换,其运算过程是 相同的,不需要额外的硬件电路。
三、大、小端字节序
在我们写代码进行调试看地址时会发现一个有趣的现象:如我的VS
#include <stdio.h>
int main()
{int a = 0x01020304;return 0;
}

我们发现其地址和我输进去的是反着来的,就和我上面画的图一样,其实这是计算机的一种存储方式——小端存储。
3.1 大小端的定义
既然有了小端存储,那么就有大段存储,那么什么是大小端呢?
其实超过⼀个字节的数据在内存中存储的时候,就有存储顺序的问题,按照不同的存储顺序,我们分 为⼤端字节序存储和⼩端字节序存储,下⾯是具体的概念:
大端(存储)模式:是指数据的低位字节内容保存在内存的⾼地址处,⽽数据的⾼位字节内容,保存 在内存的低地址处。
小端(存储)模式:是指数据的低位字节内容保存在内存的低地址处,⽽数据的⾼位字节内容,保存 在内存的⾼地址处。 上述概念需要记住,⽅便分辨⼤小端。
如图:


3.2 为什么会有大小端之分
这是因为在计算机系统中,我们是以字节为单位的,每个地址单元都对应着⼀个字节,⼀个字节为8bit位,但是在C语⾔中除了8bit的 char 之外,还有16bit的 short 型,32bit的 long 型(要看 具体的编译器),另外,对于位数大于8位的处理器,例如16位或者32位的处理器,由于寄存器宽度大于⼀个字节,那么必然存在着⼀个如何将多个字节安排的问题。因此就导致了大端存储模式和小端存 储模式。
例如:⼀个 16bit 的 short 型 x ,在内存中的地址为 0x0010 , x 的值为 0x1122 ,那么 0x11 为⾼字节, 0x22 为低字节。对于大端模式,就将 0x11 放在低地址中,即 0x0010 中, 0x22 放在⾼地址中,即 0x0011 中。小端模式,刚好相反。我们常用的 X86 结构是小端模式,而 KEIL C51 则为⼤端模式。很多的ARM,DSP都为小端模式。有些ARM处理器还可以由硬件来选择是 大端模式还是小端模式。
3.3 代码区分
那我们能不能写一个代码区分一下编译器到底是大端存储还是小端存储呢?
首先我们讲整形赋值一个1进去,这样子这个数据的低字节就有了一个1,其他的全为0。然后我们用字符型去把这个数据的第一个字节取出来,如果为1则为小端存储。反之为0则为大端存储。
代码如下:
#include <stdio.h>
int main()
{int a = 1;int* b = (char*)&a;if (*b)printf("小端");elseprintf("大端");return 0;
}四、浮点型在内存中的存储
我们谈论完了整形数据的存储,接下来我们来看一看浮点型类型的存储吧。
首先让我们想一想,浮点型的存储是否和整形一样呢?
我们可以用代码验证:
#include<stdio.h>int main()
{int n = 3;float* pFloat = (float*)&n;printf("n的值为:%d\n", n);printf("*pFloat的值为:%f\n", *pFloat);*pFloat = 3.0;printf("num的值为:%d\n", n);printf("*pFloat的值为:%f\n", *pFloat);return 0;
}结果为:

很明显的可以得出,整形和浮点型存储的方式是不一样的。
那么浮点型是怎么存储的呢?
经过我的查阅资料:
根据国际标准IEEE(电⽓和电⼦⼯程协会)754,任意⼀个⼆进制浮点数V可以表示成下面的形式:
按照上面规定的那样,十进制3.0转换为二进制的浮点数:
(十进制)3.0=(二进制)11.0 = (二进制)1.10 * 10^1
S = 0;
M = 1.10
E = 1
IEEE754规定;
对于32位的浮点数,最高的1位存储符号位S,接着的8位存储指数E,剩下的23位存储有效数字M:
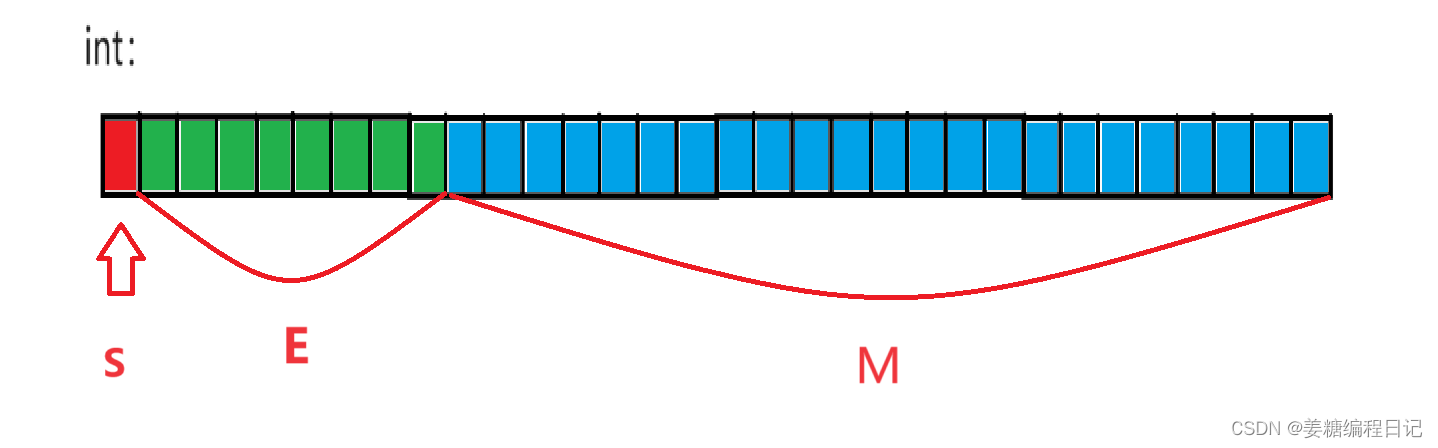
对于64位的浮点数,最高的1位存储符号位S,接着的11位存储指数E,剩下的52位存储有效数字M
IEEE 754对有效数字M和指数E,还有一些特别规定。
前面说过,1<M<2,也就是说,M可以写成1.xxxxxx的形式,其中xxxxxx表示小数部分。IEEE 754 规定,在计算机内部保存M时,默认这个数的第一位总是1,因此可以被舍去,只保存后面的xxxxxx部分。比如保存1.01的时候,只保存01,等到读取的时候,再把第一位的1加上去。这样做的目的,是节省1位有效数字。以32位浮点数为例,留给M只有23位,将第一位的1舍去以后,等于可以保存24位有效数字。
至于指数E,情况就比较复杂
首先,E为一个无符号整数(unsigned int)
这意味着,如果E为8位,它的取值范围为0~255;如果E为11位,它的取值范围为0~2047。但是,我们知道,科学计数法中的E是可以出现负数的,所以IEEE754规定,存入内存时E的真实值必须再加上一个中间数,对于8位的E,这个中间数是127;对于11位的E,这个中间数是1023。比如,2^10的E是
10,所以保存成32位浮点数时,必须保存成10+127=137,即10001001。
我们已经知道了二进制中浮点数存的过程,那么我们怎么取二进制数呢?
E分三种情况:
指数E从内存中取出还可以再分成三种情况:
E不全为0或不全为1
这时,浮点数就采用下面的规则表示,即指数E的计算值减去127(或1023),得到真实值,再将有效 数字M前加上第⼀位的1。
比如:0.5的⼆进制形式为0.1,由于规定正数部分必须为1,即将小数点右移1位,则为1.0*2^(-1),其 阶码为-1+127(中间值)=126,表示为01111110,而尾数1.0去掉整数部分为0,补⻬0到23位 00000000000000000000000,则其⼆进制表⽰形式为:
1 0 01111110 00000000000000000000000
E全为0
这时,浮点数的指数E等于1-127(或者1-1023)即为真实值,有效数字M不再加上第⼀位的1,而是还 原为0.xxxxxx的小数。这样做是为了表示±0,以及接近于0的很小的数字。
1 0 00000000 00100000000000000000000
E全为1
这时,如果有效数字M全为0,表示±无穷大(正负取决于符号位s);
1 0 11111111 00010000000000000000000
所以3.0存进去,(32位)二进制位位:
0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
五、结论
C语言的内容不止于此,还有更多需要我们共同发现,今天C语言的内存数据管理就到这里啦,如果姜糖有讲的不好的地方欢迎大家提出,谢谢大家,也希望大家能一键三连哦!
相关文章:

C语言王国——数据的内存管理
目录 一、引言 二、整形在内存中的存储 2.1 进制之间的转换 2.1.1 整形的二进制 2.1.2 十进制和二进制 2.1.3 十进制和八进制的转换 2.1.4 十六进制和十进制的转换 2.2 原码,反码,和补码 三、大、小端字节序 3.1 大小端的定义 3.2 为什么会有大…...
Kotlin 协程真的轻量吗?
前言 在官方文档的介绍中,提到了: 协程是轻量的 并给出了一个例子: fun main() = runBlocking {repeat(50_000) {// 启动大量的协程launch {delay...

Cantata 24.04 全新发布:以代码为中心的测试实现革命性升级!
简介 Cantata 24.04于2024年4月发布,以开创性的功能彻底革新了软件测试。此版本的主要功能是以代码为中心(Code-Centred)的方法,可以更快、更高效地在C/C的代码编辑器中创建单元和集成测试。 Cantata 24.04采用C中的最新标准并全…...
【问题记录】VMware 17.5.1下载VMware tools失败报错的解决方法
一,问题现象 Ubuntu可以上网,但是下载VMware tools失败,报错提示:“连接到更新服务器时发生证书错误。请检查您的Internet设置或联系您的系统管理员。” 下载安装VMware tools: 报错提示: 二࿰…...

Android - RadioGroup中多个radiobutton同时被选中问题
问题描述: 动态创建radio button, 并将多个button添加到radio group中。但是实际运行时多个radiobutton会被同时选中: 代码如下: mRadioGroup findViewById(R.id.radioGroup);mDevButtons new RadioButton[device_count];for(int i0;i<device_count;i) {mDevButtons[i] …...

如何在ElementTree文本中嵌入标签
在 ElementTree 中,你可以使用 Element 对象的方法来创建新的标签,并将其嵌入到现有的 XML 结构中。下面是一个简单的示例,演示了如何在 ElementTree 文本中嵌入新的标签: 1、问题背景 我正在使用Python ElementTree模块来处理HT…...

C语言宏定义+条件编译
1、宏定义 1.概念 C语言中的宏定义是一种预处理指令,它允许开发者为一段代码或值定义一个名称,称为宏。在编译程序时,预处理器会在实际编译之前对源代码进行预处理,将宏名称替换为其定义的内容。宏定义通常使用 #define 指令来实…...

python实现自动化测试框架如何进行数据参数化?这个包可以了解下
1.数据参数化介绍 只要你是负责编写自动化测试脚本的,数据参数化这个思想你就肯定会用 ,数据参数化的工具你肯定的懂一些 ,因为它能大大的提高我们自动化脚本编写效率 。 1.1什么是数据参数化 所谓的数据参数化 ,是指所执行的测…...

面试题:Redis和MySql数据库如何保持数据一致性?
前提引入: 在高并发的场景下,大量的请求直接访问Mysql很容易造成性能问题。所以,我们都会用Redis来做数据的缓存,削减对数据库的请求。但是,Mysql和Redis是两种不同的数据库,如何保证不同数据库之间数据的一…...

直流遥控器 继电器8-10V应用 降压恒压SL3036电源芯片
在现代电子设备中,电源的稳定性和可靠性对于设备的正常运行至关重要。特别是在直流遥控器这类设备中,由于其需要长时间稳定运行且对电压稳定性要求较高,因此选择一款合适的电源芯片显得尤为重要。本文将重点介绍SL3036电源芯片在直流遥控器继…...
论文Abstract怎么写
摘要是你要写的最后一项内容 步骤 首先先通读自己的文章,清楚自己写的文章是研究型还是技术型,适合描述性的摘要还是知识性。 描述性摘要内含研究目的、目标及方向等,不讲研究结果。字数大约100-200字。知识性摘要则包含研究结果,…...
PS系统教程19
渐变与照片调色 增加色彩背景新建图层选好渐变拉选图片渐变 与图层模式结合 也可以变换颜色 看起来比较自然,因为是与人物结合起来 也可以选择系统里面的一些色调 可以进行多次调试...

Excel函数之MAP
MAP 语法 MAP(array, [arrar2], ……, lambda(value,[value2], ……, calculation)) array:需要进行映射的数组,可以有多个 注:多个数组的形状大小尽可能保持一致,否则将出现错误值 value:数组中的每个值,每次取一个值,每个 array 按顺序对应一个 value calculation:…...
在2024年WWDC大会上,苹果宣布了其全新的“Apple Intelligence”AI功能以及ISO18功能
以下是一些主要的新增功能: Apple WWDC 2024开发者大会6月11日凌晨在总部Apple Park举行 1.智能照片编辑: 照片:AI驱动的照片润饰功能,可以根据用户描述生成自定义表情符号 2.Safari浏览助手: Safari:AI助手能够总…...
解决linux jenkins要求JDK版本与项目版本JDK不一致问题
背景–问题描述: 新入职公司,交接人说jenkins运行有问题,现在都是手动发布,具体原因让我自己看(笑哭)。我人都蒙了,测试环境都手动发布,那不是麻烦的要死! 接手后&am…...

推荐一款WPF绘图插件OxyPlot
开始 使用 NuGet 包管理器添加对 OxyPlot 的引用(如果要使用预发布包,请参阅下面的详细信息)向用户界面添加PlotView在代码中创建一个PlotModel绑定到你的属性PlotModelModelPlotView 例子 您可以在代码存储库的文件夹中找到示例。/Source/Ex…...

普通表在线重定义为分区表
普通表在线转换成分区表示例 源表表结构如下: CREATE TABLE EDC_SEPERATOR ( SEPERATOR_ID NUMBER(15) NOT NULL, EQUIPMENTINFO NVARCHAR2(20), RECORD NVARCHAR2(50), TITLE NVARCHAR2(50), ID NVARCHAR2(50), TE…...

自动驾驶场景下TCP协议参数优化调整案例分享
RTT 往返时间,从tcp协议栈决定发包,到收到回包的时间。 包含本地驱动,网卡硬件,网线,交换机,收包方处理的耗时。需注意如果开了delayed ack,协议栈未做特殊处理(默认没做ÿ…...

奇思妙想:多头RAG
大模型技术论文不断,每个月总会新增上千篇。本专栏精选论文重点解读,主题还是围绕着行业实践和工程量产。若在某个环节出现卡点,可以回到大模型必备腔调或者LLM背后的基础模型新阅读。而最新科技(Mamba,xLSTM,KAN)则提…...
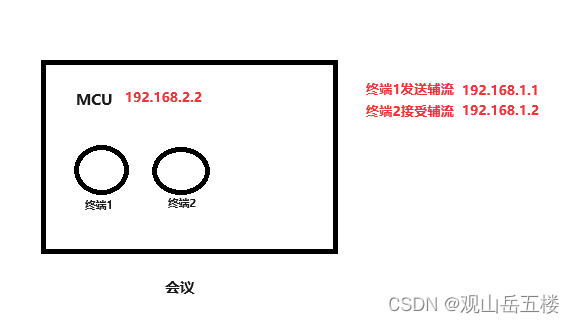
H323 截包分析辅流问题
辅流问题(h264\h264hp\h265) 终端1 : 192.168.1.1 入会发送辅流 终端2 : 192.168.1.2 入会接收辅流 问题 : 终端2不显示辅流 1、筛选 h245 h225 协议 分别筛选以下IP进行查看截包内容 (h225 || h245) && …...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...

