快速排序-Hoare 递归版 C语言

个人主页点这里~
快速排序的简介:
快速排序的关键:
设置一个key作为基准值,一般将最左边的元素作为key
详细过程:
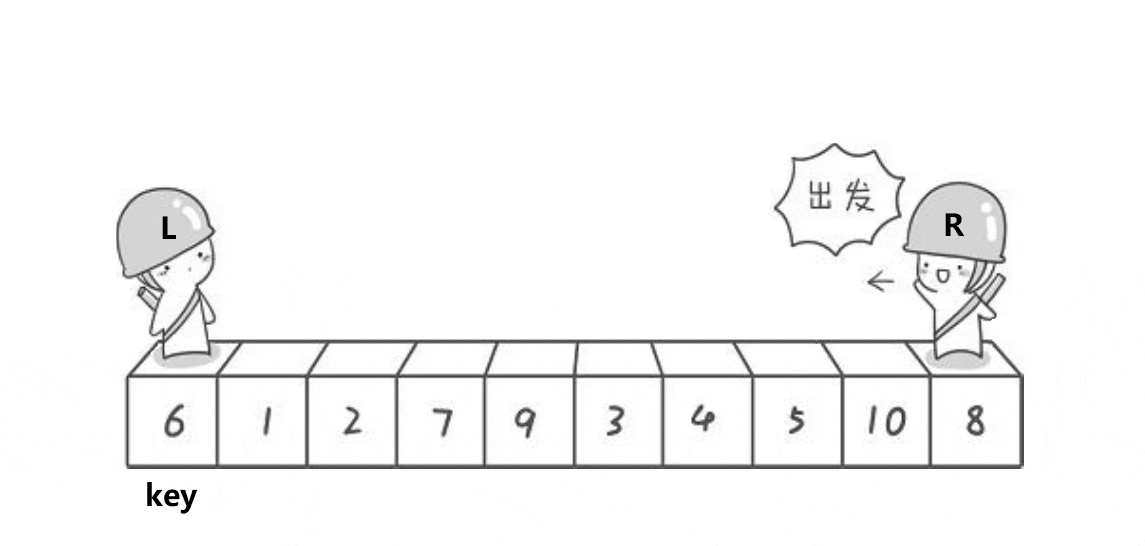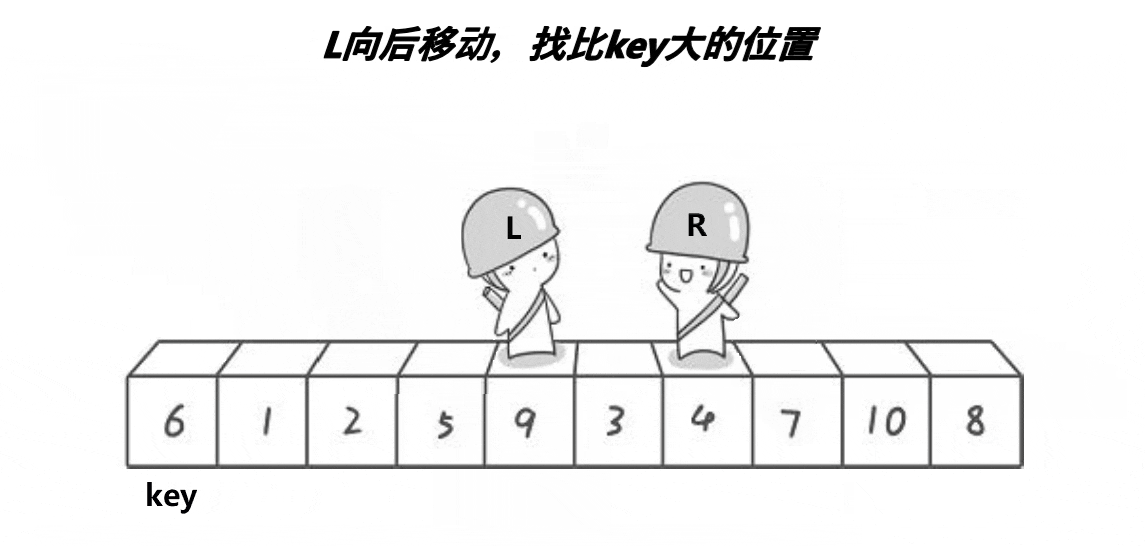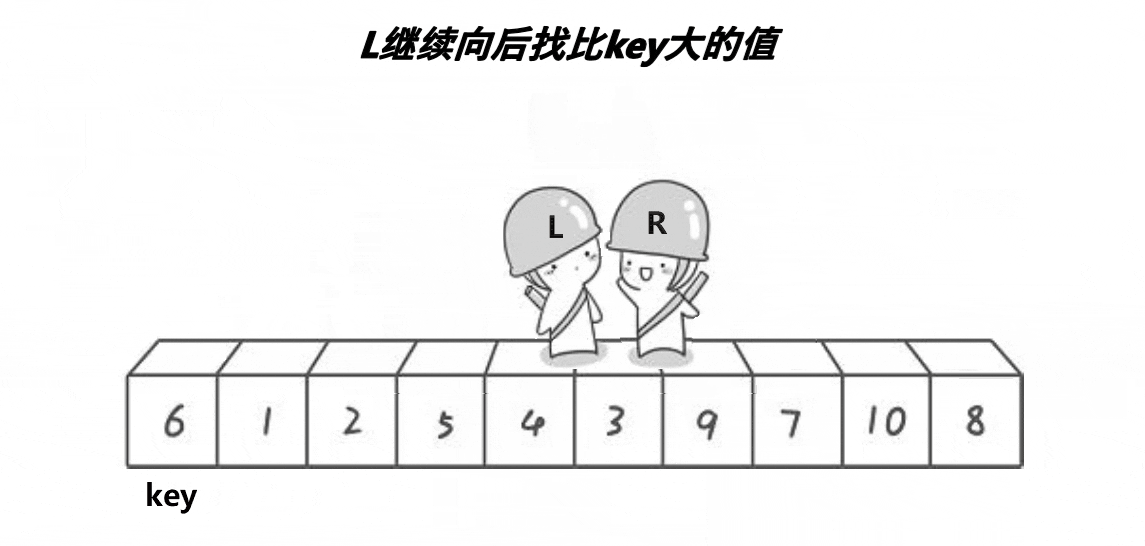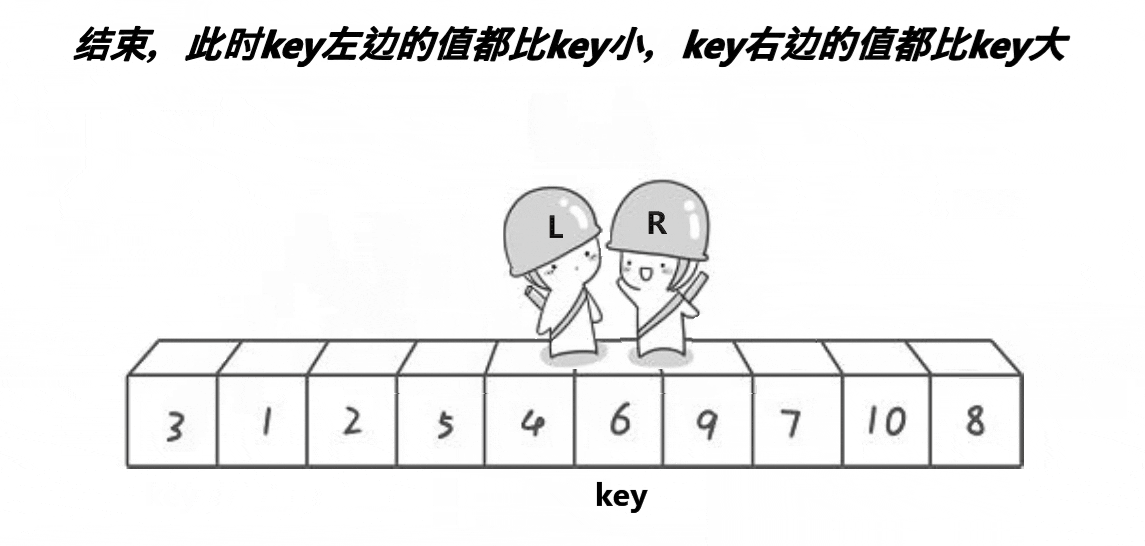
定义一个left和一个right指针作为下标分别指向无序数组的左右边界,
right从右向左走,当找到比key小的值就停下,left从左往右走,当找到比key大的值就停下,
(左边找大,右边找小)
(注意:key在左边就先走right 为什么?:我们会发现key的值一定比相遇的值要大 为什么?:因为我们先走right再走left那么循环终止只有那么情况:right找到了比key要小的值停下,然后left走到了与right相遇停止,此时相遇的值肯定是比key小的值,因为是right走到的值,相反就不行)
当两都停下时,交换两个位置的值.之后继续此过程
当两人走到相遇时停下来,交换key的值和两人相遇的值,同时更新key的位置,将key重新放到两人相遇的位置,此时会发现在key左边存放的都是比key的值小的值,右边都是大的,但并不一定时有序的
最后,以新的key为基准值,两边的区域分别递归上述过程
上述为快速排序递归实现的主框架,发现与二叉树前序遍历规则非常像,写递归框架时可想想二叉树前序遍历规则即可快速写出来
void quicksort(int* a, int left, int right)
{if (left >= right)//递归终止条件{return;}int begin = left;int end = right;int key = left;while (begin < end){while (a[end] >= a[key] && begin < end){end--;}while (a[begin] <= a[key] && begin < end){begin++;}Swap(&a[begin], &a[end]);}Swap(&a[key], &a[begin]);key = begin;quicksort(a, left, key - 1);//左区间quicksort(a, key + 1, right);//右区间
}可以优化的两点(两个问题):
1.解决问题:避免了循环直接到相遇的情况
在快速排序中,选择基准元素key的方式会影响算法的性能。
如果选择的基准元素总是接近待排序序列的中位数,那么算法的性能会接近最优(即时间复杂度为O(n log n))。然而,如果选择的基准元素总是接近待排序序列的边界值(即最大或最小值),那么算法的性能会退化到接近冒泡排序(即时间复杂度为O(n^2))。
当基准元素接近待排序序列的中位数时:
- 左边和右边的子序列长度大致相等。这意味着递归调用的深度较小,同时每次递归处理的数据量也大致相等,这使得算法能够保持较为均匀的分割,从而充分利用分治策略的优势。
- 递归树较为平衡,每个子问题的规模都大致相等。这有助于减少算法中的比较次数和交换次数,从而提高算法的效率。
当基准元素接近待排序序列的边界值(即最大或最小值)时:
- 左边或右边的子序列可能非常长,而另一个子序列则可能很短。这会导致递归调用的深度增加,同时每次递归处理的数据量也会变得不均匀。
- 递归树变得不平衡,一些子问题的规模很小,而另一些子问题的规模则很大。这会增加算法中的比较次数和交换次数,从而降低算法的效率。
在最坏的情况下,当每次选择的基准元素都是待排序序列的最小值或最大值时,快速排序会退化为冒泡排序。这是因为每次分割后,其中一个子序列的长度为0(即没有元素需要排序),而另一个子序列的长度则为n-1(即除了基准元素外的所有元素)。这样,算法需要执行n-1次递归调用,每次递归调用只减少一个元素,实际上就变成了冒泡排序的效果。
解决方法:三数取中
// 三数取中,取中间大的
// 解决问题1:避免了循环直接到相遇的情况
int getmid(int* a, int left, int right)
{int mid = (left + right) / 2;if (a[left] < a[mid]){if (a[mid] < a[right]){return mid;}else if (a[left < right]){return right;}else{return left;}}else{if (a[left] < a[right]){return left;}else if (a[mid] > a[right]){return mid;}else{return right;}}
}
void quicksort(int* a, int left, int right)
{if (left >= right){return;}//三数取中int mid = getmid(a, left, right);Swap(&a[mid], &a[left]);int begin = left;int end = right;int key = left;while (begin < end){while (a[end] >= a[key] && begin < end){end--;}while (a[begin] <= a[key] && begin < end){begin++;}Swap(&a[begin], &a[end]);}Swap(&a[key], &a[begin]);key = begin;quicksort(a, left, key - 1);quicksort(a, key + 1, right);
}
解决问题2:当递归排序到后面剩下10个数左右时,递归开辟的栈帧
以key为基准开辟左右两个栈帧,类似于二叉树,消耗几乎一半的栈帧(二叉树往下子树越多),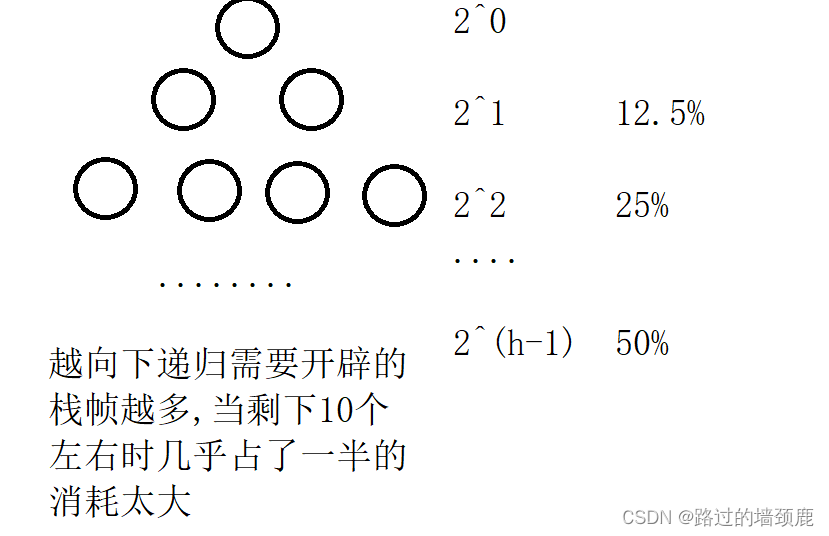
解决方法:小区间优化
所以我们在是剩下10个左右元素个数((right - left + 1) < 10)需要排序时,不要再递归,而是调用其他合适排序算法进行排序
void Swap(int* p1, int* p2)
{int tmp = *p1;*p1 = *p2;*p2 = tmp;
}void printarr(int* a, int sz)
{for (int i = 0; i < sz; i++){printf("%d ", a[i]);}printf("\n");
}// 三数取中,取中间大的
// 解决问题1:避免了循环直接到相遇的情况
int getmid(int* a, int left, int right)
{int mid = (left + right) / 2;if (a[left] < a[mid]){if (a[mid] < a[right]){return mid;}else if (a[left < right]){return right;}else{return left;}}else{if (a[left] < a[right]){return left;}else if (a[mid] > a[right]){return mid;}else{return right;}}
}void insertsort(int* a, int sz)
{for (int i = 0; i < sz - 1; i++){int end = i;int tmp = a[end + 1];while (end >= 0){if (a[end] > tmp){a[end + 1] = a[end];end--;}else{break;}}a[end + 1] = tmp;}
}
void quicksort(int* a, int left, int right)
{if (left >= right){return;}// 以key为基准开辟左右两个栈帧,类似于二叉树// 解决问题2:当递归排序到后面剩下10个数左右时,递归开辟的栈帧// 消耗几乎一半的栈帧(二叉树往下子树越多),// 所以我们可以在这时候调用 简单的其他排序来优化// 小区间优化if ((right - left + 1) < 10){//插入排序insertsort(a + left, right - left + 1);}else{//三数取中int mid = getmid(a, left, right);Swap(&a[mid], &a[left]);int begin = left;int end = right;int key = left;while (begin < end){while (a[end] >= a[key] && begin < end){end--;}while (a[begin] <= a[key] && begin < end){begin++;}Swap(&a[begin], &a[end]);}Swap(&a[key], &a[begin]);key = begin;quicksort(a, left, key - 1);quicksort(a, key + 1, right);}
}分享结束啦!个人主页点这里~
相关文章:

快速排序-Hoare 递归版 C语言
个人主页点这里~ 快速排序的简介: 快速排序是Hoare于1962年提出的一种 二叉树结构 的 交换 排序方法,其基本思想为:任取待排序元素序列中 的某元素作为 基准值 ,按照该排序码将待排序集合分割成 两子序列 , 左子序列中所有元素均 …...

C语言经典指针运算笔试题图文解析
指针运算常常出现在面试题中,画图解决是最好的办法。 题目1: #include <stdio.h> int main() {int a[5] { 1, 2, 3, 4, 5 };int* ptr (int*)(&a 1);printf("%d,%d", *(a 1), *(ptr - 1));return 0; } //程序的结果是什么&…...

使用 KubeKey v3.1.1 离线部署原生 Kubernetes v1.28.8 实战
今天,我将为大家实战演示,如何基于操作系统 openEuler 22.03 LTS SP3,利用 KubeKey 制作 Kubernetes 离线安装包,并实战离线部署 Kubernetes v1.28.8 集群。 实战服务器配置 (架构 1:1 复刻小规模生产环境,配置略有不…...

DOS 命令
Dos: Disk Operating System 磁盘操作系统, 简单说一下 windows 的目录结构。 ..\ 到上一级目录 常用的dos 命令: 查看当前目录是有什么内容 dir dir d:\abc2\test200切换到其他盘下:盘符号 cd : change directory 案例演示:切换…...

如何用Java程序实现一个简单的消息队列?
在Java程序中,可以使用内置的java.util.concurrent.BlockingQueue作为消息队列存放的容器,来实现一个简单的消息队列。 具体实现如下,在这个例子中,我们创建了一个生产者线程和一个消费者线程,他们共享同一个阻塞队列…...

OpenAI 宕机事件:GPT 停摆的影响与应对
引言 2024年6月4日,OpenAI 的 GPT 模型发生了一次全球性的宕机,持续时间长达8小时。此次宕机不仅影响了OpenAI自家的服务,还导致大量用户涌向竞争对手平台,如Claude和Gemini,结果也导致这些平台出现故障。这次事件的广…...

linux常用的基础命令
ls - 列出目录内容。 cd - 更改目录。 pwd - 打印当前工作目录。 mkdir - 创建新目录。 rmdir - 删除空目录。 touch - 创建新文件或更新现有文件的时间戳。 cp - 复制文件或目录。 mv - 移动或重命名文件或目录。 rm - 删除文件或目录。 cat - 显示文件内容。 more - 分页显示…...

618家用智能投影仪推荐:这个高性价比品牌不容错过
随着科技的不断进步,家庭影院的概念已经从传统的大屏幕电视逐渐转向了更为灵活和便携的家用智能投影仪。随着618电商大促的到来,想要购买投影仪的用户们也开始摩拳擦掌了。本文将从投影仪的基础知识入手,为您推荐几款性价比很高的投影仪&…...

自愿离婚协议书
自愿离婚协议书 男方(夫): 女方(妻): 双方现因 原因,导致夫妻情感已破裂,自愿离婚…...

WPS JSA 宏脚本入门和样例
1入门 WPS window版本才支持JSA宏的功能。 可以自动化的操作文档中的一些内容。 参考文档: WPS API 参考文档:https://open.wps.cn/previous/docs/client/wpsLoad 微软的Word API文档:Microsoft.Office.Interop.Word 命名空间 | Microsoft …...
Printing and Exporting
打印 大多数DevExpress。NET控件(XtraGrid、XtraPivotGrid、XttraTreeList、XtraScheduler、XtraCharts)提供打印和导出功能。 所有可打印的DevExpress.NET控件是使用XtraPrinting库提供的方法打印的。 若要确定预览和打印选项是否可用,请检…...
c++【入门】正多边形每个内角的度数
限制 时间限制 : 1 秒 内存限制 : 128 MB 题目 根据多边形内角和定理,正多边形内角和等于:(n - 2)180(n大于等于3且n为整数)(如下图所示是三角形、四边形、五边形、六边形的形状)…...

spring boot3登录开发-邮箱登录/注册接口实现
⛰️个人主页: 蒾酒 🔥系列专栏:《spring boot实战》 🌊山高路远,行路漫漫,终有归途 目录 写在前面 上文衔接 内容简介 功能分析 所需依赖 邮箱验证登录/注册实现 1.创建交互对象 2.登录注册业务逻辑实…...

数据结构-二叉搜索树
二叉搜索树:BST(Binary Search Tree) 二叉搜索树是二叉树,可以为空,如果不为空,满足以下性质: 非空左子树的所有键值小于其根节点的键值非空右子树的所有键值大于其根节点的键值左、右字数本身也都是二叉搜索树 二叉…...

JUnit:Java开发者不可或缺的单元测试框架
在软件开发过程中,测试是确保代码质量的关键环节。单元测试作为测试体系的基础,对提升代码质量、降低bug率、增强软件稳定性具有重要作用。JUnit 作为 Java 语言事实上的标准单元测试框架,已经成为 Java 开发者进行单元测试的首选工具。本文将…...

NG32单片机GPIO口配置方式
目录 一、引言 二、GPIO口基本结构 三、GPIO口配置方式 四、工作原理 五、总结 一、引言 NG32单片机是一款集成度高、功能强大的微控制器。其中,GPIO(General Purpose Input/Output)口作为单片机与外部设备通信的重要接口,具…...
SpringCloud-OpenFeign拓展-连接池、最佳使用方法、日志输出
目录 1 OpenFeign连接池 1.1 常见连接类型 1.2 连接池使用方法 1.2.1 引入依赖 1.2.2 开启连接池功能 1.2.3 配置完成,重启实例即可,底层将更改设置。 2 OpenFeign最佳使用方法 2.1 每个微服务都是单独的project,内部有三个独立模块 …...

跨链协议中Cosmos IBC、Polkadot/XCM、Celer Network的区别以及用途
跨链协议是实现不同区块链之间通信和价值转移的关键技术。Cosmos IBC、Polkadot/XCM 和 Celer Network 是三个在跨链领域内具有代表性的协议,它们各自有着独特的设计理念和应用场景。下面是这三个协议的详细对比: Cosmos IBC (Inter-Blockchain Communi…...
电子画册制作与传统画册相比,有哪些优势?
在当今数字化时代,电子画册作为一种新兴的媒体形式,其制作与传统画册相比具有显著的优势。以下是对这些优势的详细探讨。 首先,电子画册的制作过程通常更加便捷和经济。相较于传统画册需要经历的繁琐的印刷过程,电子画册的制作大多…...
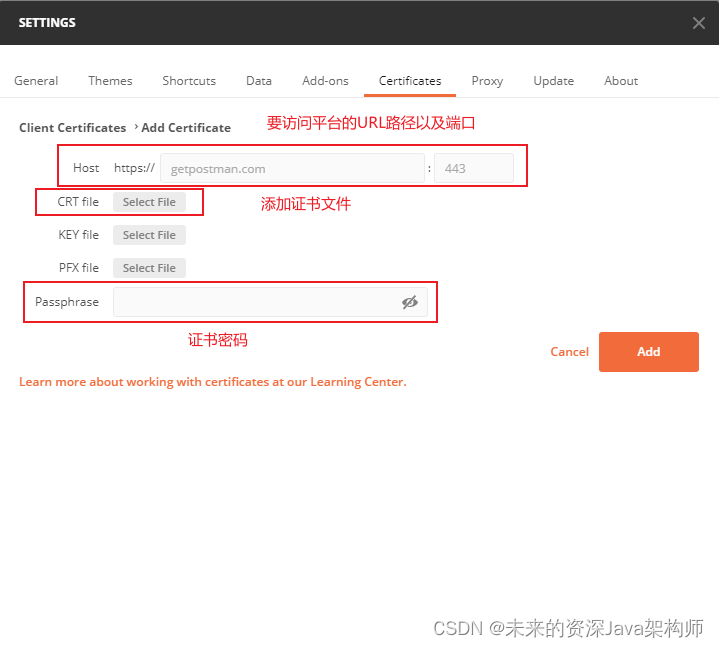
postman如何导入证书
1、打开postman,点击Settings。 2、添加证书。 3、填写要访问平台的URL路径及端口、证书文件、证书密码。 4、添加完之后即可立即调用postman。...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...
