分治与递归
实验一:分治与递归
【实验目的】
深入理解分治法的算法思想,应用分治法解决实际的算法问题。
【实验性质】
验证性实验(学时数:2H)
【实验内容与要求】
1、设有n=2k个运动员要进行网球循环赛。现要设计一个满足以下要求的比赛日程表:⑴每个选手必须与其他n-1个选手各赛一次;⑵每个选手一天只能赛一次;⑶循环赛一共进行n-1天。按此要求可将比赛日程表设计成有n行和n列的一个表。表中第一列是选手编号,表中第i行和第j列(j>1)处填入第i个选手在第j天所遇到的选手。例如8个选手的日程表安排如右图所示。
要求:请设计算法,并采用C或C++语言编写程序实现上述功能,调试运行并对算法的时间复杂度进行分析。
【算法思想及处理过程】
首先,通过输入参赛人数n,判断n是否合法(是否为2的幂次方),如果不合法则输出错误信息。
然后,输入第一个选手的编号k。
调用roundrob函数,传入参数k和n。roundrob函数的作用是生成对阵表。
首先,判断n是否为2,如果是,则直接生成对阵表。对阵表是一个二维数组a,每个元素表示某个选手与另一个选手的对阵情况。
如果n不是2,递归调用roundrob函数,将n除以2传入,并分成两个子问题,分别解决。
递归结束后,对阵表的前一半行和后一半行进行交换,生成完整的对阵表。
最后,遍历对阵表,并输出每个元素的值。
在主函数中,先判断n是否合法,如果合法则调用roundrob函数生成对阵表,并输出。
如果n不合法,则直接返回。
【程序代码】
#include <stdio.h>
#include<iostream>
using namespace std;
int a[100][100]{};
void roundrob(int k, int n)
{
if (n == 2)
{
a[k][0] = k + 1;
a[k][1] = k + 2;
a[k + 1][0] = k + 2;
a[k + 1][1] = k + 1;
}
else
{
roundrob(k,n / 2);
roundrob(k + n / 2,n / 2);
}
for (int i = k; i < k + n / 2; i++)
{
for (int j = n / 2; j < n; j++)
{
a[i][j] = a[i + n / 2][j - n / 2];
}
}
for (int i = k + n / 2; i < k + n; i++)
{
for (int j = n / 2; j < n; j++)
{
a[i][j] = a[i - n / 2][j - n / 2];
}
}
}
int determine(int n)
{
if (n % 2 == 0)
{
if (n / 2 == 1) return 1;
determine(n / 2);
}
else
{
cout << "输入人数不合法" << endl;
return 0;
}
}
int main()
{
int n;
int k;
cout << "请输入参赛人数" << endl;
cin >> n;
if (determine(n) == 1)
{
cout << "请输入第一个选手编号" << endl;
cin >> k;
k = k - 1;
roundrob(k, n);
int i = 0, j = 0;
for (i = 0; i < n; i++)
{
for (j = 0; j < n; j++)
{
cout << a[i][j] << " ";
}
cout << endl;
}
}
if (determine(n) == 0)
{
return 0;
}
}
【运行结果】
程序运行结果截图。
【算法分析】
代码的时间复杂度为O(n^2),其中n为参赛人数。代码中使用递归的方式生成了一个二维数组a,数组的大小为n×n。在生成数组a的过程中,有两个嵌套的循环,每个循环的次数都是n/2,因此循环次数总共为n/2 × n/2 = n^2/4,所以时间复杂度为O(n^2)。另外,代码中还有一个determine函数,该函数的时间复杂度为O(logn),因为每次递归都将n除以2,直到n为偶数。
相关文章:

分治与递归
实验一:分治与递归 【实验目的】 深入理解分治法的算法思想,应用分治法解决实际的算法问题。 【实验性质】 验证性实验(学时数:2H) 【实验内容与要求】 1、设有n2k个运动员要进行网球循环赛。现要设计一个满足以…...

Spring中IOC容器
IoC IOC容器 IoC是一种设计思想,面向对象编程 Spring通过IoC管理所有Java对象的实例化和初始化,控制对象之间依赖关系 将IoC容器管理的Java对象称为Spring Bean,与new创建的对象没有区别 控制反转(IoC Inversion of Controle&a…...

php redis分布式锁
一,概念 在PHP中实现分布式锁通常可以使用数据库、缓存系统(如Redis)或者其他中央存储系统来保证在分布式系统中的数据一致性与同步。秒杀下单、抢红包等等业务场景,都需要用到分布式锁。 常规方案大概有七中 方案一:…...

kotlin 中的布尔
1、kotlin中内置的Boolean类型,可以有true与false两个值的布尔对象。 布尔值的内置运算有(跟很多语言如java、js一摸一样): ||——逻辑或&&——逻辑与!——逻辑非 fun main() {val a: Boolean trueval b: Boolean fa…...

有哪些ai聊天推荐?简单分享三款
有哪些ai聊天推荐?在当今数字化时代,人工智能(AI)聊天软件已经成为我们日常生活中不可或缺的一部分。无论是与朋友、家人还是同事交流,这些智能聊天软件都能为我们提供极大的便利。那么,市面上有哪些值得推…...
Python第二语言(十、Python面向对象(上))
目录 1. 标记变量的基础类型 2. 初识对象 2.1 使用对象组织数据 3. 成员变量 3.1 类和类成员的定义 3.2 成员变量和成员方法使用 3.3 成员方法的定义语句 4. 类和对象class Clock: def ring(self): 4.1 创建类对象的语法:对象名 类名称() 4.2 用生活中的…...
SolidWorks 2016 SP5安装教程
软件介绍 Solidworks软件功能强大,组件繁多。 Solidworks有功能强大、易学易用和技术创新三大特点,这使得SolidWorks 成为领先的、主流的三维CAD解决方案。 SolidWorks 能够提供不同的设计方案、减少设计过程中的错误以及提高产品质量。SolidWorks 不仅…...

为什么高考志愿只选计算机专业?
刚刚高考结束,不知道各位学弟学妹考的怎么样啊? 高考毕竟是对十二年寒窗苦读的评判,也是很多人改变命运的机会。很多同学每天等待出分的过程很煎熬,既吃不好也玩不好(os:这种同学还挺多的)。 但…...

GPT大模型微调-提高垂直领域回答质量
微调一个大模型并测试微调后的效果是一个很好的学习实践。下面是一个逐步指导,帮助你使用一个较小的预训练大模型进行微调,并测试其效果。我们将使用 Hugging Face 的 Transformers 库和一个较小的预训练模型,如 DistilBERT。这个库非常流行且易于使用。 实现步骤 步骤 1:…...

全网首发-Docker被封后的代理设置教程
最近上交、科大以及阿里的一些docker镜像,好像都因为不可控力导致无法访问。 所以,之前好多正常的一些镜像的打包都会报错: 比如: #1 [internall load build definition from Dockerfile#1transferring dockerfile:972B done#1 D…...

代码随想录算法训练营第五十七天|1143.最长公共子序列、1035.不相交的线、53. 最大子序和、392.判断子序列
代码随想录算法训练营第五十七天 1143.最长公共子序列 题目链接:1143.最长公共子序列 确定dp数组以及下标的含义:dp[i][j] :以下标i - 1为结尾的text1,和以下标j - 1为结尾的text2,最长重复子数组长度为dp[i][j]确…...
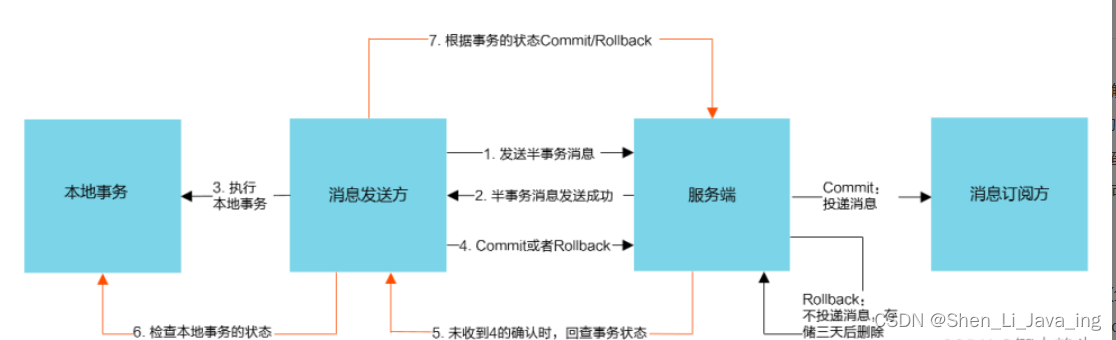
RocketMQ事务性消息
RocketMQ事务性消息是一定能保证消息发送成功的 事务消息发送步骤: (1)发送方将半事务消息发送至RocketMQ服务端。 (2)RocketMQ服务端将消息持久化之后,向发送方返回ack确认消息已经发送成功。由于消息为…...

mysql (事物)
一.什么是事物 事物是一组操作的集合,不可分割的工作单位,事物会把所有的操作当作一个整体一起向系统提交或撤销操作请求,就是这些操作要么一起成功要么一起失败。 二.事物操作 (这个就是一个理解) 1.事务特性 原子性…...
kotlin 中的字符串
一、字符类访问 1、字符串的访问跟js一样,可以使用索引来访问或者直接循环。 fun main() {val a: String "2024"// 方式一:for (item in a) {println(item) // 输出每一个字符}// 方式二:println("${a[0]}, ${a[1]}, ${a[2…...
网站线上模板建设的优缺点
优点: 1.搭建的时间短,在线建站,只需要登录注册然后选择网站模板创建网站即可管理自己的网站后台,就几步操作就可以实现。 2.网站出错率少,因为有很多用户在使用,前期所报出来的问题就已经一一…...

哲学家进餐问题
1.最多允许四个哲学家同时进餐,保证有一个筷子是空闲的,从而保证能有有一个哲学家成功进餐,而不导致死锁 semaphore chopstick[5] {1, 1, 1, 1, 1}, mutex4; Pi(){do{think...P(mutex);P(chopstick[i]);P(chopstick[(i1)%5);eat...V(mutex)…...

无人机遥感在农林信息提取中的实现方法与GIS融合应用
在新一轮互联网信息技术大发展的现今,无人机、大数据、人工智能、物联网等新兴技术在各行各业都处于大爆发的前夜。为了将人工智能方法引入农业生产领域。首先在种植、养护等生产作业环节,逐步摆脱人力依赖;在施肥灌溉环节构建智慧节能系统&a…...
笔试60%)
联想测开一面(电话面试)笔试60%
联想测开一面(电话面试)笔试60% 3.21 无自我介绍 基本问项目,问实习 对python自动化测试了解多少 讲一下python中打包和解包的概念 学校无测试相关课程,平时用什么平台去学习的 计算机底层实现原理简要说说(软硬结合&…...
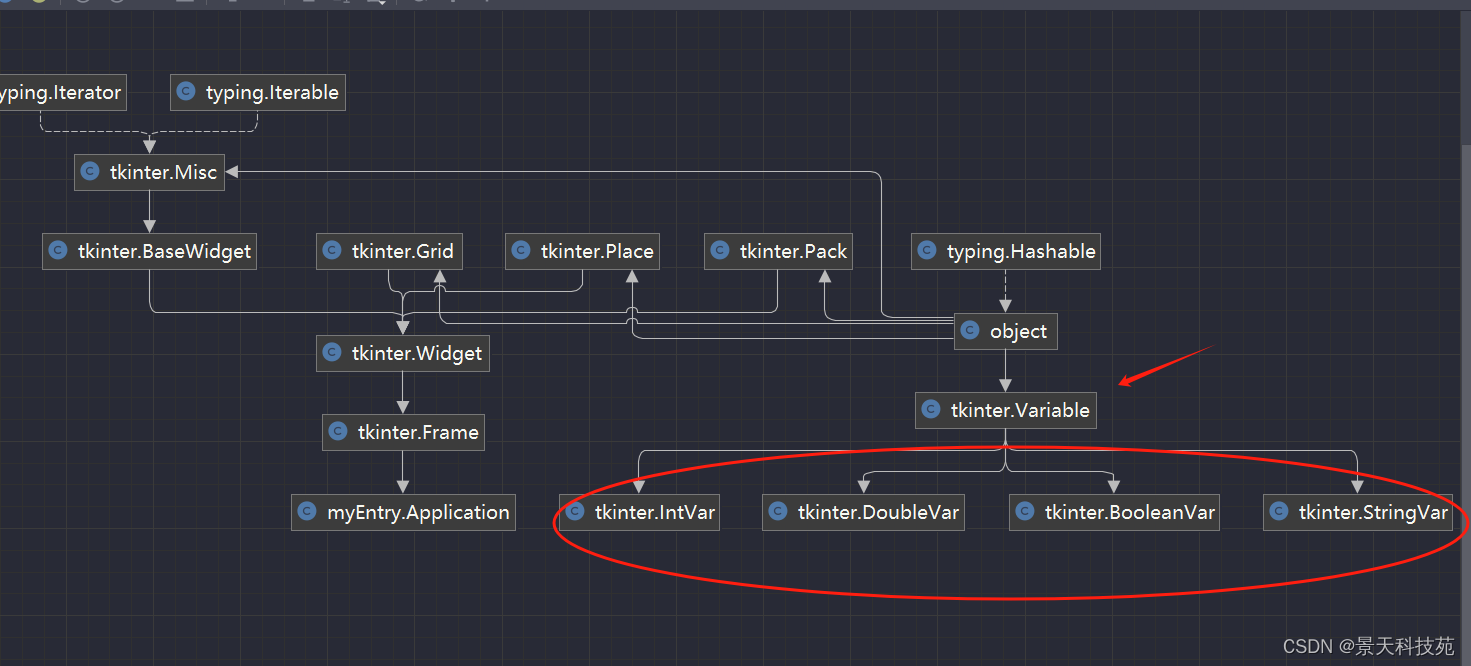
【python】tkinter GUI开发: Button和Entry的应用实战探索
✨✨ 欢迎大家来到景天科技苑✨✨ 🎈🎈 养成好习惯,先赞后看哦~🎈🎈 🏆 作者简介:景天科技苑 🏆《头衔》:大厂架构师,华为云开发者社区专家博主,…...
)
sm2证书生成(openssl3.0)
1、下载安装包 https://www.openssl.org/source/openssl-3.0.14.tar.gz 2、解压到指定位置 /appserver/openssl-3.0.14 3、安装依赖包 yum -y install gcc perl make zlib-devel perl-CPAN 4、编译 ./config shared --prefix/appserver/SM make depend make make install 5…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...
