计算机视觉全系列实战教程:(八)图像变换-点运算、灰度变换、直方图变换
图像变换:点运算、灰度变换、直方图变换
- 1.点运算
- (1)What
- (2)Why
- 2.灰度变换
- (1)What
- (2)Why(作用)
- (3)Which(有哪些灰度变换)
- 3.直方图修正
- (1)直方图均衡化
1.点运算
(1)What
通过点运算,输出图像的每个像素的灰度值仅仅取决于输入图像中相对应像素的灰度值。
(2)Why
点运算的作用:实现图像增强的常用方法之一
2.灰度变换
(1)What
灰度变换是一种点运算的具体形式,换句话说,灰度变换是点运算的一种运用
(2)Why(作用)
增强对比度,是增强图像的重要手段(途径)和方法
- 改善图像的质量:显示更多细节,进行对比度拉伸
- 突出感兴趣的特征:针对图像中感兴趣的区域进行突出或抑制
(3)Which(有哪些灰度变换)
核心:灰度变换函数的不同
- A.线性灰度变换
y = k * f(x) + b
当k>1:对比度将增大
当k<1:对比度将减小
当k=1,b!=0:图像整体变亮或变暗
当k=-1,b=255:图像灰度正好相反
当k<0,b>0:暗区域变亮,亮区域变暗 - B.分段线性灰度变换

确定分段函数的三个k值和b值即可实现分段灰度变换效果。
分段线性灰度变换的效果对参数的选取依赖很高,当参数选取不好的时候,不但无法实现增强图像的效果,还可能变得更加糟糕。为此实现自适应选取成为分段线性灰度变换的关键。目前常用的方法有:自适应最小误差法、多尺度逼近方法
和 恒增强率方法等。
- C.非线性变换-对数变换
g(x) = c * log(1+f(x)) - D.非线性变换-反对数变换
g(x) = ( (f(x)+1)^r -1 ) / f(x) - E.非线性变换-幂律变换
g(x) = c*f(x)^alpha
3.直方图修正
(1)直方图均衡化
直方图均衡化可实现图像的自动增强,但效果不易控制,得到的是全局增强的结果
- step01:统计每一个灰度级的数量
// 统计输入图像的灰度级数量
std::vector<int> vNk(256, 0);
int iTotal = imDst.total();
for (int i = 0; i < imDst.total(); ++i)
{vNk[imDst.data[i]]++;
}
- step02:求累积分布
// 求累积分布函数
for (int i = 1; i < 256; ++i)
{vNk[i] = vNk[i] + vNk[i - 1];
}
- step03:建立映射关系
// 确定映射关系
std::vector<double> vMPk(256, 0.0);
for (int i = 0; i < 256; ++i)
{vMPk[i] = 255.0f * (double)vNk[i] / iTotal;
}
// 重新赋值实现均衡化
for (int i = 0; i < iTotal; ++i)
{imDst.data[i] = vMPk[imDst.data[i]];
}
代码汇总如下(可直接使用):
/* 图像均衡化 */
int ImgEqualize(const cv::Mat& imSrc, cv::Mat& imDst) {// 对输入的数据进行可靠性判定if (imSrc.empty()) return -1;// 对输入图像进行灰度化处理if (imSrc.channels() == 3)cv::cvtColor(imSrc, imDst, cv::COLOR_RGB2GRAY);else imDst = imSrc;// 统计输入图像的灰度级数量std::vector<int> vNk(256, 0);int iTotal = imDst.total();for (int i = 0; i < imDst.total(); ++i){vNk[imDst.data[i]]++;}// 求累积分布函数for (int i = 1; i < 256; ++i){vNk[i] = vNk[i] + vNk[i - 1];}// 确定映射关系std::vector<double> vMPk(256, 0.0);for (int i = 0; i < 256; ++i){vMPk[i] = 255.0f * (double)vNk[i] / iTotal;}// 重新赋值实现均衡化for (int i = 0; i < iTotal; ++i){imDst.data[i] = vMPk[imDst.data[i]];}}
相关文章:

计算机视觉全系列实战教程:(八)图像变换-点运算、灰度变换、直方图变换
图像变换:点运算、灰度变换、直方图变换 1.点运算(1)What(2)Why 2.灰度变换(1)What(2)Why(作用)(3)Which(有哪些灰度变换) 3.直方图修正(1)直方图均衡化 1.点运算 (1)What 通过点运算,输出图像的每个像素的灰度值仅仅取决于输入图像中相对应…...

4.MongoDB sharding Cluster 分片集群
MongoDB分片集群的介绍: 是MongoDB提供的一种可水平扩展的数据存储解决方案。 当单个MongoDB服务器无法满足数据存储需求或吞吐量要求时,可以使用分片集群来分散数据量和查询负载。分片集群的结构组成: 1.分片(shards)…...

PDF转图片工具
背景: 今天有个朋友找我:“我有个文件需要更改,但是文档是PDF的,需要你帮我改下内容,你是搞软件的,这个对你应该是轻车熟路了吧,帮我弄弄吧”,听到这话我本想反驳,我是开…...

Day 19:419. 甲板上的战舰
Leetcode 419. 甲板上的战舰 给你一个大小为 m x n 的矩阵 board 表示甲板,其中,每个单元格可以是一艘战舰 ‘X’ 或者是一个空位 ‘.’ ,返回在甲板 board 上放置的 战舰 的数量。 战舰 只能水平或者垂直放置在 board 上。换句话说ÿ…...

Web前端专科实习:技能提升、实践挑战与职业展望
Web前端专科实习:技能提升、实践挑战与职业展望 在数字化时代,Web前端技术作为连接用户与互联网世界的桥梁,其重要性日益凸显。作为一名Web前端专科实习生,我有幸在这个充满机遇和挑战的领域进行实践学习。接下来,我将…...

简单脉冲动画效果实现
简单脉冲动画效果实现 效果展示 CSS 知识点 CSS 变量的灵活使用CSS 动画使用 页面整体结构实现 <div class"pulse"><span style"--i: 1"></span><span style"--i: 2"></span><span style"--i: 3"…...

apache poi 插入“下一页分节符”并设置下一节纸张横向的一种方法
一、需求描述 我们知道,有时在word中需要同时存在不同的节,部分页面需要竖向、部分页面需要横向。本文就是用java调用apache poi来实现用代码生成上述效果。下图是本文实现的效果,供各位看官查阅,本文以一篇课文为例,…...

【React】useCallback和useMemo使用指南
useCallback和useMemo是React中两个用于优化性能的Hooks。以下是它们的使用指南,分点表示并归纳了关键信息: useCallback useCallback返回一个记忆化的回调函数,该回调函数只在它的依赖项发生改变时才会更新。这对于在组件渲染之间保持稳定的引用特别有用,可以防止不必要…...
XMind软件下载-详细安装教程视频
简介 XMind是一款实用的思维导图软件,简单易用、美观、功能强大,拥有高效的可视化思维模式,具备可扩展、跨平台、稳定性和性能,真正帮助用户提高生产率,促进有效沟通及协作。中文官方网站:http://www.x…...
一个小的画布Canvas页面,记录点的轨迹
Hello大家好,好久没有更新了,最近在忙一些其他的事,今天说一下画布canvas,下面是我的代码,实现了一个点从画布的(0,0)到(canvas.width,canvas.height)的一个实…...
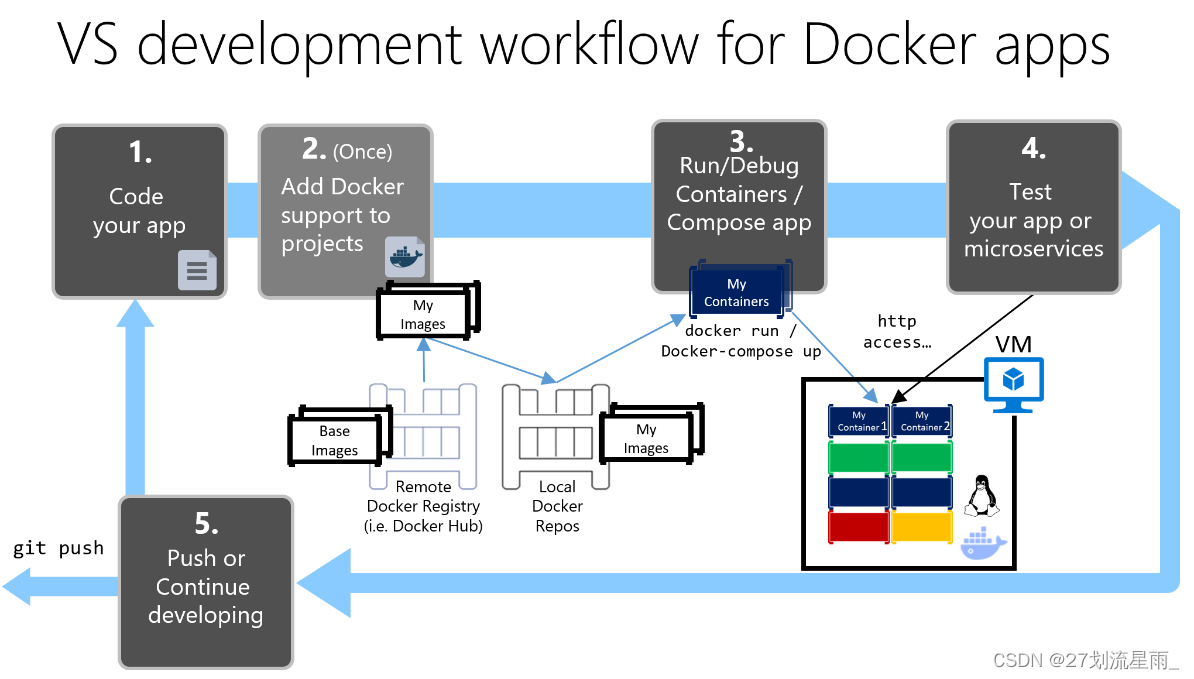
docker-compose教程
1. docker-compose是什么? 1. 1 简介 compose、machine 和 swarm 是docker 原生提供的三大编排工具。 简称docker三剑客。Compose 项目是 Docker 官方的开源项目,定义和运行多个 Docker 容器的应用(Defining and running multi-container Do…...

结果出乎意料!MySQL和MariaDB谁快?MySQL 8.0比MySQL 5.6快吗?
MySQL和MariaDB哪个更快?MySQL 8.0的版本和早期MySQL 5.6的版本哪个更快?这儿有个第三方的测试报告回答了这两个大家关心的问题,姚远来和大家一起解读一下。https://smalldatum.blogspot.com/2024/04/sysbench-on-small-server-mariadb-and.h…...

Alienware外星人X17R2 原装Win11系统镜像下载 带SupportAssist OS Recovery一键恢复
装后恢复到您开箱的体验界面,包括所有原机所有驱动AWCC、Mydell、office、mcafee等所有预装软件。 最适合您电脑的系统,经厂家手调试最佳状态,性能与功耗直接拉满,体验最原汁原味的系统。 原厂系统下载网址:http://w…...

【NI国产替代】高速数据采集模块,最大采样率为 125 Msps,支持 FPGA 定制化
• 双通道高精度数据采集 • 支持 FPGA 定制化 • 双通道高精度采样率 最大采样率为 125 Msps12 位 ADC 分辨率 最大输入电压为 0.9 V -3 dB 带宽为 30 MHz 支持 FPGA 定制化 根据需求编程实现特定功能和性能通过定制 FPGA 实现硬件加速,提高系统的运算速度FPGA…...
【网络安全的神秘世界】2024.6.6 Docker镜像停服?解决最近Docker镜像无法拉取问题
🌝博客主页:泥菩萨 💖专栏:Linux探索之旅 | 网络安全的神秘世界 | 专接本 解决Docker镜像无法拉取问题 🙋♂️问题描述 常用镜像站:阿里云、科大、南大、上交等,全部挂掉 执行docker pull命…...

【Python入门与进阶】1基本输入和输出
基本输入输出 1.等号赋值 1.1 基本赋值 number_110number_1 1.2 多个赋值 number_2number_3number_420 number_2 number_3 number_4 1.3 多重赋值 number_5,number_6,number_730,35,40 number_5 number_6 number_7 1.4 下划线赋值 _50 _ 2.命名规则 注意:…...

CTF Show MISC做题笔记
MISCX 30 题目压缩包为misc2.rar,其中包含三个文件:misc1.zip, flag.txt, hint.txt。其中后两个文件是加密的。 先解压出misc1.zip, 发现其中包含两个文件:misc.png和music.doc。其中后面文件是加密的。 解压出misc.png,发现图片尾部有消息:flag{flag…...
【QT5】<总览二> QT信号槽、对象树及常用函数
文章目录 前言 一、QT信号与槽 1. 信号槽连接模型 2. 信号槽介绍 3. 自定义信号槽 二、QT的对象树 三、添加资源文件 四、样式表的使用 五、QSS文件的使用 六、常用函数与宏 前言 承接【QT5】<总览一> QT环境搭建、快捷键及编程规范。若存在版…...

Button按钮类
自学python如何成为大佬(目录):https://blog.csdn.net/weixin_67859959/article/details/139049996?spm1001.2014.3001.5501 按钮是GUI界面中应用最为广泛的控件,它常用于捕获用户生成的单击事件,其最明显的用途是触发绑定到一个处理函数。 wxPython类…...
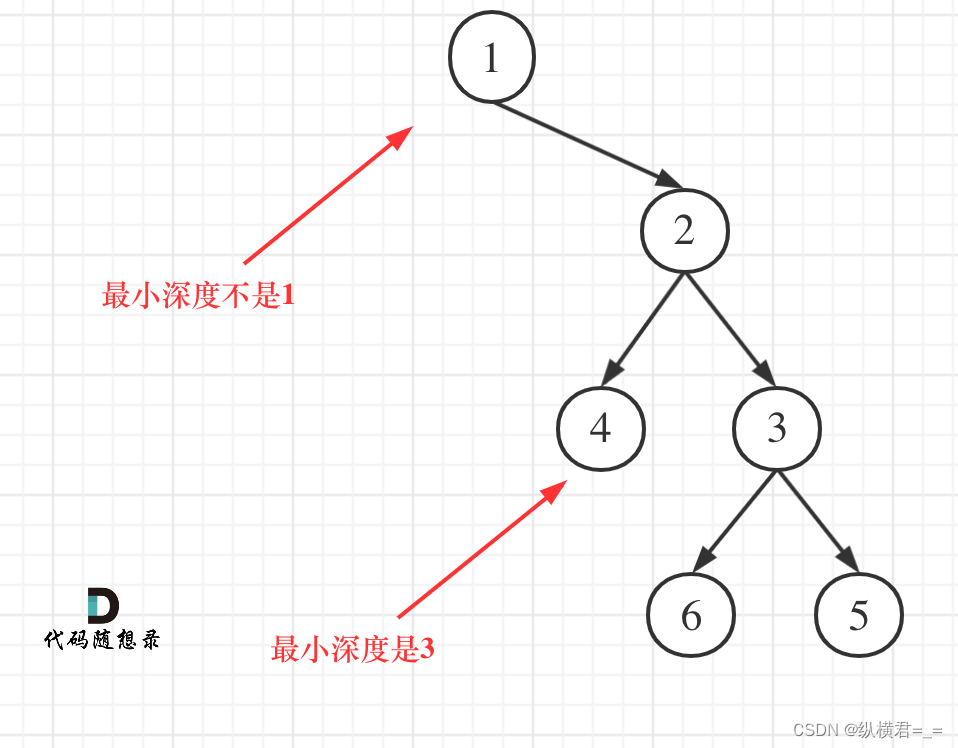
代码随想录-二叉树 | 111 二叉树的最小深度
代码随想录-二叉树 | 111 二叉树的最小深度 LeetCode 111 二叉树的最小深度解题思路代码难点总结 LeetCode 111 二叉树的最小深度 题目链接 代码随想录 题目描述 给定一个二叉树,找出其最小深度。 最小深度是从根节点到最近叶子节点的最短路径上的节点数量。 说…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...

JavaScript 数据类型详解
JavaScript 数据类型详解 JavaScript 数据类型分为 原始类型(Primitive) 和 对象类型(Object) 两大类,共 8 种(ES11): 一、原始类型(7种) 1. undefined 定…...

Windows安装Miniconda
一、下载 https://www.anaconda.com/download/success 二、安装 三、配置镜像源 Anaconda/Miniconda pip 配置清华镜像源_anaconda配置清华源-CSDN博客 四、常用操作命令 Anaconda/Miniconda 基本操作命令_miniconda创建环境命令-CSDN博客...
