【优选算法】优先级队列 {优先级队列解决TopK问题,利用大小堆维护数据流的中位数}
一、经验总结
优先级队列(堆),常用于在集合中筛选最值或解决TopK问题。
提示:对于固定序列的TopK问题,最优解决方案是快速选择算法,时间复杂度为O(N)比堆算法O(NlogK)更优;而对于动态维护数据流中的TopK,最优解决方案是堆算法,每次添加数据后筛选,时间复杂度为O(logK)比快速选择算法O(N)更优;
优先级队列如何解决TopK问题?
- 创建一个大小为K的堆
- 循环
- 将数组中的元素依次进堆
- 判断堆中的元素个数是否大于K,如果大于K就pop弹出堆顶元素
- 将数组中的所有元素全部筛选一遍后,堆中剩余的K个元素就是最大(小)的K个元素
TopK问题选用大根堆还是小根堆?
- 如果要选出最大的K个数,就选用小根堆;
- 如果要选出最小的K个数,就选用大根堆;
利用大小堆维护数据流中的中位数
- 创建一个大堆left用于存储数据流的前一半(升序),一个小堆right用于存储后一半
- 控制left的元素个数m和right的元素个数n满足:m==n或m==n+1
- 数据流的中位数:当m==n时,mid=(left.top()+right.top())/2;当m==n+1时,mid=left.top();
- 新增元素:将新元素与left.top()(或right.top())比较,决定加入left还是right。完成插入后,记得调整两个堆的元素个数使其满足规则。
二、相关编程题
2.1 最后一块石头的重量
题目链接
1046. 最后一块石头的重量 - 力扣(LeetCode)
题目描述

算法原理
利用堆结构筛选最大值
编写代码
class Solution {
public:int lastStoneWeight(vector<int>& stones) {priority_queue<int> heap;for(auto e : stones) heap.push(e);while(heap.size() >= 2){int s1 = heap.top();heap.pop();int s2 = heap.top();heap.pop();if(s1 > s2) heap.push(s1-s2);}if(heap.size() == 0) return 0;else return heap.top();}
};
2.2 数据流中的第 K 大元素
题目链接
703. 数据流中的第 K 大元素 - 力扣(LeetCode)
题目描述

算法原理

这道题更适合使用堆解决,因为add函数插入一个数字后返回当前数据中的第K大的元素,如果使用快速选则算法,复杂度为O(N);而使用堆算法,复杂度为O(logK)
编写代码
class KthLargest {priority_queue<int, vector<int>, greater<int>> _heap;int _k;
public:KthLargest(int k, vector<int>& nums) {_k = k;for(auto e : nums) add(e);}int add(int val) {_heap.push(val);if(_heap.size() > _k)_heap.pop();return _heap.top();}
};
2.3 前K个高频单词
题目链接
692. 前K个高频单词 - 力扣(LeetCode)
题目描述

算法原理

编写代码
class Solution {typedef pair<string, int> PSI;struct Cmp{bool operator()(const PSI &left, const PSI &right){if(left.second != right.second) //出现频次不同,选出高频单词,按照小根堆的方式排列return left.second > right.second;elsereturn left.first < right.first; //出现频次相同,按字典序排序,按照大根堆的方式排列}};
public:vector<string> topKFrequent(vector<string>& words, int k) {unordered_map<string, int> hash;priority_queue<PSI, vector<PSI>, Cmp> heap;vector<string> ret(k);//统计所有单词的出现频次for(auto &str:words){++hash[str];} //用一个大小为k的堆筛选TopKfor(auto &psi:hash){heap.push(psi);if(heap.size() > k)heap.pop();}//将结果倒着放入数组for(int i = k-1; i >= 0; --i){ret[i] = heap.top().first;heap.pop();}return ret;}
};
2.4 数据流的中位数
题目链接
295. 数据流的中位数 - 力扣(LeetCode)
题目描述

算法原理

编写代码
class MedianFinder {priority_queue<int> left; //大根堆priority_queue<int, vector<int>, greater<int>> right; //小根堆
public:MedianFinder() {}void addNum(int num) {if(left.size() > right.size()) //m > n{int x = left.top();if(num <= x){left.push(num);left.pop();right.push(x);}else{right.push(num);}}else //m == n{int y = right.empty()? 0:right.top();if(right.empty() || num < y){left.push(num);}else{right.push(num);right.pop();left.push(y);}}}double findMedian() {if(left.size() > right.size()) //m > nreturn (double)left.top();else //m == nreturn (left.top()+right.top())/2.0;}
};
相关文章:

【优选算法】优先级队列 {优先级队列解决TopK问题,利用大小堆维护数据流的中位数}
一、经验总结 优先级队列(堆),常用于在集合中筛选最值或解决TopK问题。 提示:对于固定序列的TopK问题,最优解决方案是快速选择算法,时间复杂度为O(N)比堆算法O(NlogK)更优;而对于动态维护数据流…...
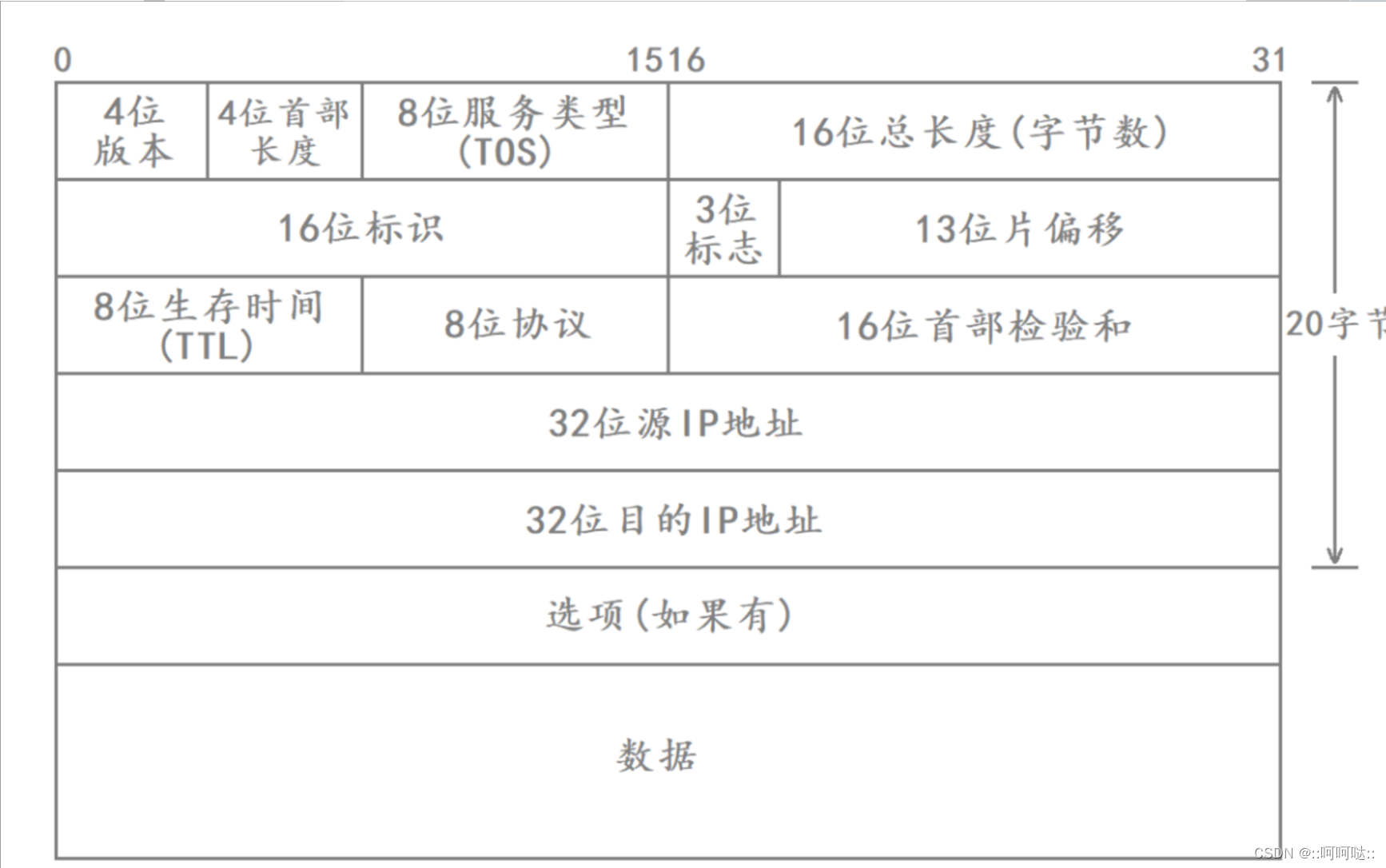
11 IP协议 - IP协议头部
什么是 IP 协议 IP(Internet Protocol)是一种网络通信协议,它是互联网的核心协议之一,负责在计算机网络中路由数据包,使数据能够在不同设备之间进行有效的传输。IP协议的主要作用包括寻址、分组、路由和转发数据包&am…...

【java】【python】leetcode刷题记录--二叉树
144.二叉树的前序遍历 题目链接 前、中、后的遍历的递归做法实际上都是一样的,区别就是遍历操作的位置不同。 对于先序遍历,也就是先根,即把查看当前结点的操作放在最前面即可。 class Solution {public List<Integer> preorderTrav…...
EVA-CLIP实战
摘要 EVA-CLIP,这是一种基于对比语言图像预训练(CLIP)技术改进的模型,通过引入新的表示学习、优化和增强技术,显著提高了CLIP的训练效率和效果。EVA-CLIP系列模型在保持较低训练成本的同时,实现了与先前具有相似参数数量的CLIP模型相比更高的性能。特别地,文中提到的EV…...

限定法术施放目标
实现目标 法术只对特定 creature | gameobject 施放,否则无法施放 实现方法 conditions SourceTypeOrReferenceId:13(CONDITION_SOURCE_TYPE_SPELL_IMPLICIT_TARGET)SourceGroup:受条件影响的法术效果掩码…...

【通信原理】数字频带传输系统
二进制数字调制,解调原理:2ASK,2FSK 二进制数字调制,解调原理:2PSK,2DPSK 二进制数字已调制信号的功率谱 二进制数字调制系统的抗噪声性能 二进制调制系统的性能总结...
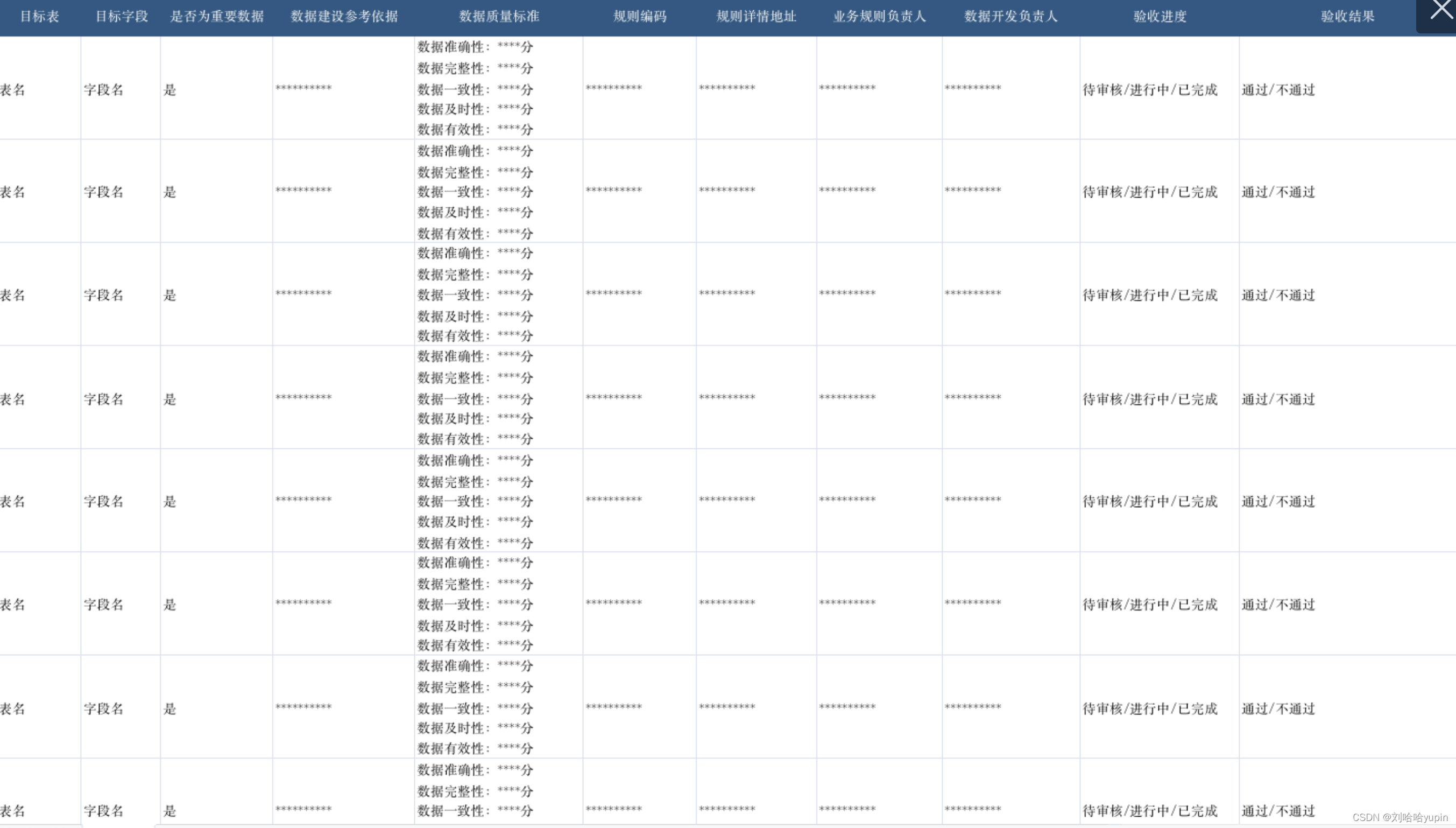
数据价值管理-数据验收标准
前情提要:数据价值管理是指通过一系列管理策略和技术手段,帮助企业把庞大的、无序的、低价值的数据资源转变为高价值密度的数据资产的过程,即数据治理和价值变现。第一讲介绍了业务架构设计的基本逻辑和思路。前面我们讲完了数据资产建设标准…...

vue3模板语法总结
1. 响应式数据 Vue 3中的数据是响应式的,即当数据发生变化时,视图会自动更新。这是通过使用JavaScript的getter和setter来实现的。 2. 组件化 Vue 3采用组件化开发方式,允许创建可复用的组件。 每个组件都有自己的作用域,并且…...
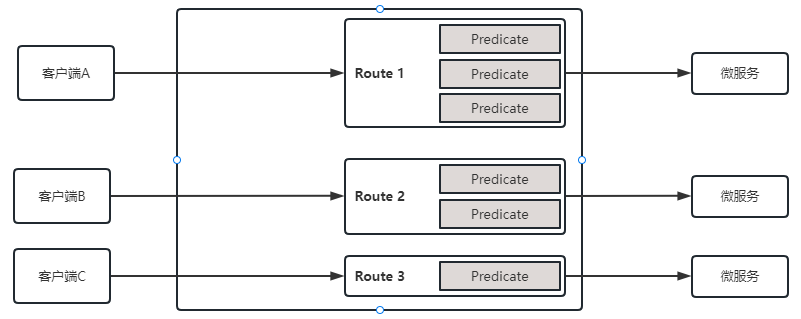
Spring Cloud 之 GateWay
前言 前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家:https://www.captainbed.cn/z ChatGPT体验地址 文章目录 前言前言1、通过API网关访问服务2、Spring Cloud GateWay 最主要的功能就是路由…...

可转债全部历史因子数据,提供api支持
今天在写可转债系统,顺便下载了一下服务器的可转债数据,给大家研究使用 from trader_tool.stock_data import stock_datafrom trader_tool.lude_data_api import lude_data_apiimport osclass convertible_bond_back_test_system: 可转债回测系统…...

Python | C++ | MATLAB | Julia | R 市场流动性数学预期评估量
🎯要点 🎯市场流动性策略代码应用:🎯动量策略:滚动窗口均值策略、简单移动平均线策略、指数加权移动平均线策略、相对强弱指数、移动平均线收敛散度交叉策略、三重指数平均策略、威廉姆斯 %R 策略 | 🎯均值…...

Android 常用开源库 MMKV 源码分析与理解
文章目录 前言一、MMKV简介1.mmap2.protobuf 二、MMKV 源码详解1.MMKV初始化2.MMKV对象获取3.文件摘要的映射4.loadFromFile 从文件加载数据5.数据写入6.内存重整7.数据读取8.数据删除9.文件回写10.Protobuf 实现1.序列化2.反序列化 12.文件锁1.加锁2.解锁 13.状态同步 总结参考…...
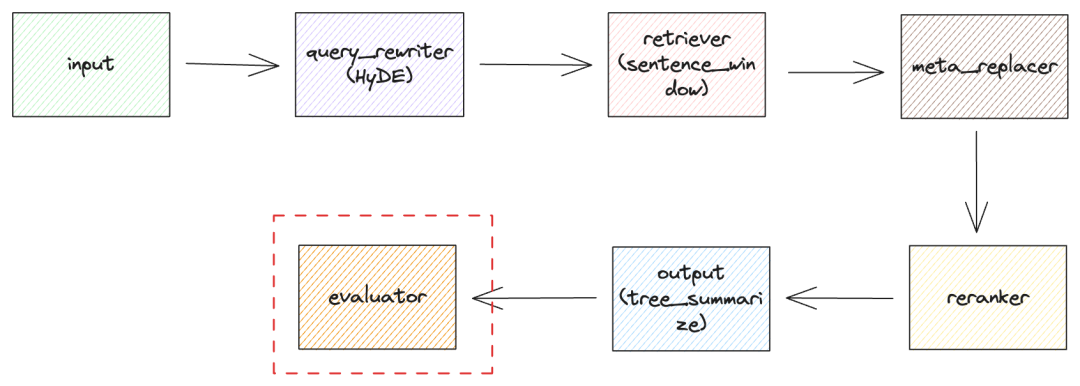
大模型高级 RAG 检索策略之流程与模块化
我们介绍了很多关于高级 RAG(Retrieval Augmented Generation)的检索策略,每一种策略就像是机器中的零部件,我们可以通过对这些零部件进行不同的组合,来实现不同的 RAG 功能,从而满足不同的需求。 今天我们…...

TCPListen客户端和TCPListen服务器
创建项目 TCPListen服务器 public Form1() {InitializeComponent();//TcpListener 搭建tcp服务器的类,基于socket套接字通信的//1创建服务器对象TcpListener server new TcpListener(IPAddress.Parse("192.168.107.83"), 3000);//2 开启服务器 设置最大…...

DDei在线设计器-属性编辑器
DDei-Core-属性编辑器 DDei-Core-属性编辑器插件包含了文本、大文本、数值、下拉、单选、勾选以及颜色等属性编辑。 图形和属性共同构成一个完整的定义,属性编辑器就是编辑属性值的控件。当选中图形实例时,属性面板就会展现当前实例的所有属性以及属性编…...

八字综合测算网整站源码程序/黄历/灵签/排盘/算命/生肖星座/日历网/周公解梦
八字综合测算网整站源码程序/黄历/灵签/排盘/算命/生肖星座/日历网/周公解梦 演示地址: https://s24.gvyun.com/ 手机端地址: https://ms24.gvyun.com/ 网站功能分类: 八字:八字测算;日干论命;称骨论命…...
—— 布局管理)
C# WPF入门学习主线篇(十一)—— 布局管理
C# WPF入门学习主线篇(十一)—— 布局管理 欢迎来到C# WPF入门学习系列的第十一篇。在前面的文章中,我们已经探讨了WPF中的许多控件及其属性和事件。今天,我们将开启一个新的篇章——布局管理。布局管理是WPF中一个至关重要的概念…...

LabVIEW轴承试验机测控系统
开发了一种基于LabVIEW软件开发的大功率风电机组增速箱轴承试验机测控系统。系统主要用于模拟实际工况,进行轴承可靠性分析,以优化风电机组的性能和可靠性。通过高度自动化的测控系统,实现了对试验机的精确控制,包括速度、振动、温…...
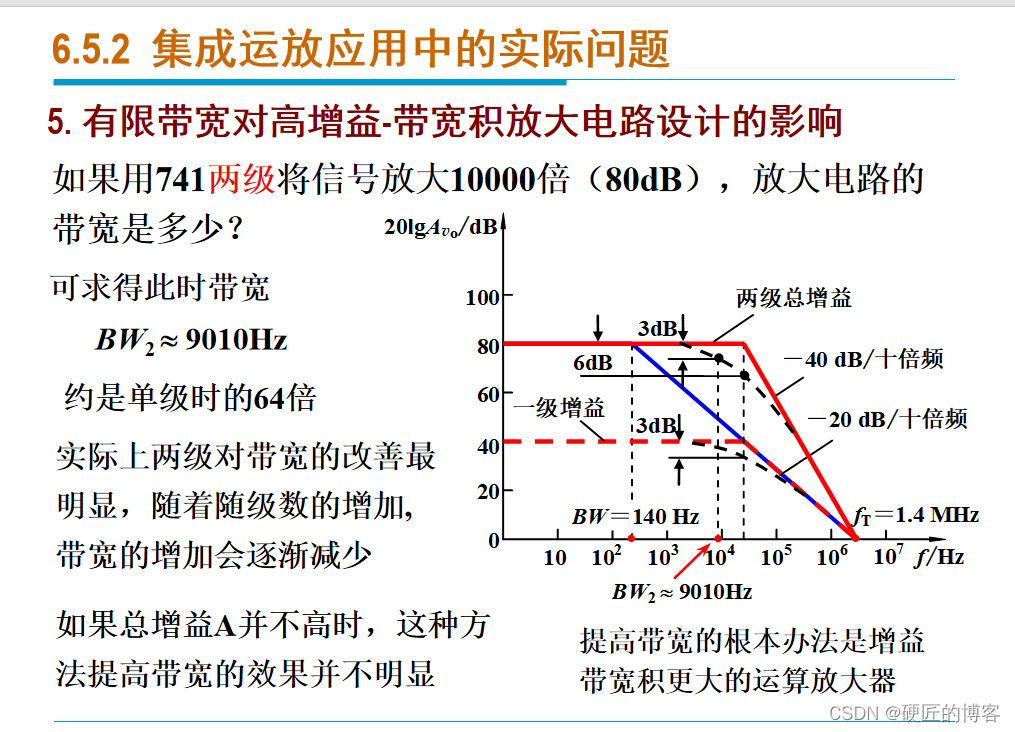
0605 实际集成运算放大器的主要参数和对应用电路的影响
6.5.1 实际集成运放的主要参数 6.5.2 集成运放应用中的实际问题 6.5.2 集成运放应用中的实际问题...
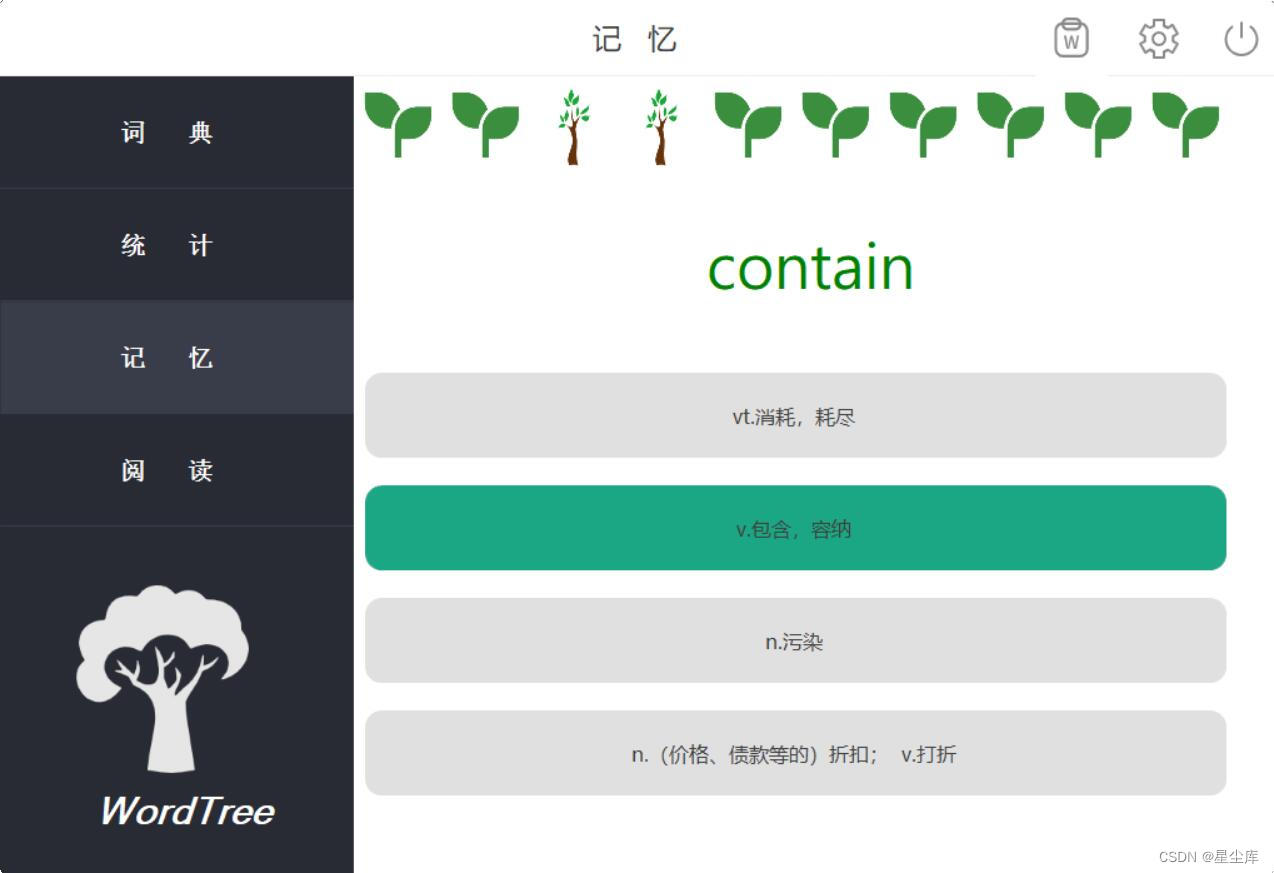
艾宾浩斯winform单词系统+mysql
为用户提供集词典、题库、记忆单词功能于一体的应用,为用户提供目的性强、科学高效、多样化的记忆单词方法,使用户学习英语和记忆单词的效率得到提高 单词记忆模块 管理模块 查询单词 阅读英文 查看词汇 记忆单词 收藏单词 字段管理设置 统计 艾宾浩斯wi…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...

uniapp 开发ios, xcode 提交app store connect 和 testflight内测
uniapp 中配置 配置manifest 文档:manifest.json 应用配置 | uni-app官网 hbuilderx中本地打包 下载IOS最新SDK 开发环境 | uni小程序SDK hbulderx 版本号:4.66 对应的sdk版本 4.66 两者必须一致 本地打包的资源导入到SDK 导入资源 | uni小程序SDK …...

WebRTC从入门到实践 - 零基础教程
WebRTC从入门到实践 - 零基础教程 目录 WebRTC简介 基础概念 工作原理 开发环境搭建 基础实践 三个实战案例 常见问题解答 1. WebRTC简介 1.1 什么是WebRTC? WebRTC(Web Real-Time Communication)是一个支持网页浏览器进行实时语音…...

永磁同步电机无速度算法--基于卡尔曼滤波器的滑模观测器
一、原理介绍 传统滑模观测器采用如下结构: 传统SMO中LPF会带来相位延迟和幅值衰减,并且需要额外的相位补偿。 采用扩展卡尔曼滤波器代替常用低通滤波器(LPF),可以去除高次谐波,并且不用相位补偿就可以获得一个误差较小的转子位…...
