Python | C++ | MATLAB | Julia | R 市场流动性数学预期评估量
🎯要点
🎯市场流动性策略代码应用:🎯动量策略:滚动窗口均值策略、简单移动平均线策略、指数加权移动平均线策略、相对强弱指数、移动平均线收敛散度交叉策略、三重指数平均策略、威廉姆斯 %R 策略 | 🎯均值回归策略:布林线交易策略、配对交易策略 | 🎯基于数学模型的策略:通过每月交易最小化投资组合波动策略、每月交易的最大夏普比率策略 | 🎯基于时间序列预测的策略:具有外生回归量的季节性自回归综合移动平均线、先知策略 | 🎯市场流动性差价数学评估。
🎯个人现金流建模预期市场投资模式。
🎯风险获利数学模型:Python流动性做市风险获利 | 信息不对称买卖数学模型 | 🎯市场机制分析:Python牛市熊市横盘机制 | 缺口分析 | 头寸调整算法 | 🎯资产评估:Python和MATLAB及C++资产价格看涨看跌对冲模型和微积分 | 🎯金融数学代码:C++和Python计算金融数学方程算法模型
🍇Python季节性和外部因素计算模型
时间序列数据中的季节性是指在一段时间内以固定间隔出现的重复且可预测的模式。这些模式可以以各种形式表现出来,例如每日、每周、每月或每年的周期,并且通常受天气、假期或经济季节等外部因素的影响。季节性的存在意味着数据在特定时间范围内重复出现系统性变化。了解季节性对于准确预测至关重要,因为它有助于捕捉数据的周期性。分析师使用各种统计技术来检测和建模季节性,从而使他们能够做出更明智的决策和预测。季节性分解、傅里叶分析和自相关函数是用于分析和解决时间序列数据中季节性的常用工具。通过确认和整合这些重复模式,预测模型可以更好地捕捉数据的固有结构并提供更可靠的预测。
处理时间序列数据中的季节性涉及建模和整合定期观察到的重复模式。假设您有冰淇淋销售的每日数据,并且您注意到一种季节性模式,即夏季销售额趋于增加,冬季销售额趋于减少。要处理这种季节性,您可以按照以下步骤使用此模型:
💦差分(积分):
季节性模式会使数据变得不平稳。如果需要,可以应用差分使序列平稳。这可能涉及取一阶差分或应用季节性差分,具体取决于数据的特征。季节性差分通常用于使时间序列平稳。差分参数表示为 d(表示季节性差分)。差分涉及从其滞后版本中减去时间序列。第 d 次差分可以表示为:
Y t ′ = Y t − Y t − d Y_t^{\prime}=Y_t-Y_t-d Yt′=Yt−Yt−d
这里, Y t ′ Y_t^{\prime} Yt′是差分序列,是季节周期。
💦识别季节性因素
通过纳入季节性自回归 (SAR) 和季节性移动平均 (SMA) 项来建模季节性差异。这些项捕捉特定时间间隔(季节)内数据中的重复模式。为了识别时间序列的季节性成分,我们可以使用各种分解技术。一种常见的方法是使用 LOESS (STL) 进行季节性趋势分解。这有助于识别趋势、季节性和残差成分。这些成分可以帮助识别定期重复出现的模式,从而更好地理解模型。
计算移动平均线以捕捉趋势。我们可以使用简单的移动平均线或指数平滑等其他技术。在这里,我们使用移动平均线。
移动平均值是通过取指定周期数(本例中为 m)内的值的平均值来计算的。
S M A ( t ) = ( Y t − k + 1 + … + Y t ) / k S M A(t)=\left(Y_{t-k+1}+\ldots+Y_t\right) / k SMA(t)=(Yt−k+1+…+Yt)/k
其中, Y t Y_t Yt 是时间 t 的值, k k k 是移动平均线的周期数。
它对于消除短期波动和突出数据的整体方向特别有用。从原始时间序列中减去移动平均线以获得去趋势序列。
去趋势序列 = y t − 移动平均线 \text { 去趋势序列 }=y_t-\text { 移动平均线 } 去趋势序列 =yt− 移动平均线
其中,n 是季节数。
n 的选择取决于数据季节性的周期性。例如,如果您观察每年的季节性,则每月数据的 n 将设置为 12。残差表示考虑了趋势和季节性成分后时间序列中的剩余变化。
残差 = 去趋势序列季节分量 \text { 残差 }=\text { 去趋势序列季节分量 } 残差 = 去趋势序列季节分量
它有助于定义时间序列数据中无法解释的变化或噪声残差对于模型诊断和验证非常重要。一个好的预测模型应该具有随机的残差,并且没有明显的模式。如果残差中存在模式,则表明该模型可能需要进一步细化。
综上所述,模型可表示为:
Θ ( L ) p θ ( L s ) P Δ d Δ s D y t = Φ ( L ) q ϕ ( L s ) Q Δ d Δ s D ϵ t + ∑ i = 1 n β i x t i \Theta(L)^p \theta\left(L^s\right)^P \Delta^d \Delta_s^D y_t=\Phi(L)^q \phi\left(L^s\right)^Q \Delta^d \Delta_s^D \epsilon_t+\sum_{i=1}^n \beta_i x_t^i Θ(L)pθ(Ls)PΔdΔsDyt=Φ(L)qϕ(Ls)QΔdΔsDϵt+i=1∑nβixti
Θ ( L ) ν θ ( L s ) P Δ d Δ s D y t \Theta(L)^\nu \theta\left(L^s\right)^P \Delta^d \Delta_s^D y_t Θ(L)νθ(Ls)PΔdΔsDyt:表示因变量,表示为 y t y_{t} yt,它可能是一个时间序列变量。
Θ ( L ) p θ ( L s ) P \Theta(L)^p \theta\left(L^s\right)^P Θ(L)pθ(Ls)P:分别涉及自回归 (AR) 和季节性自回归分量。 Δ d Δ s D \Delta^d \Delta_s^D ΔdΔsD 表示差分,通常用于实现时间序列数据的平稳性。 ϵ t \epsilon_t ϵt 表示模型的误差项。 ∑ i = 1 n β i x t i \sum_{i=1}^n \beta_i x_t^i ∑i=1nβixti 包括 (n) 个外生变量 x t i x_t^i xti 与相应的系数 β i \beta_i βi。
💦Python实现模型:
from datetime import datetime
import numpy as np
import pandas as pd
import matplotlib.pylab as plt
%matplotlib inline
from matplotlib.pylab import rcParamsfrom statsmodels.tsa.stattools import adfuller
from statsmodels.tsa.seasonal import seasonal_decomposedf = pd.read_csv("https://raw.githubusercontent.com/AirP.csv")将“月”列转换为日期时间格式并将其设置为 DataFrame 的索引。
df['Month'] = pd.to_datetime(df['Month'], infer_datetime_format=True)
df = df.set_index(['Month'])差分
df['#Passengers_diff'] = df['#Passengers'].diff(periods=12)
df.info()输出:
<class 'pandas.core.frame.DataFrame'>
DatetimeIndex: 144 entries, 1949-01-01 to 1960-12-01
Data columns (total 2 columns):# Column Non-Null Count Dtype
--- ------ -------------- ----- 0 #Passengers 144 non-null int64 1 #Passengers_diff 132 non-null float64
dtypes: float64(1), int64(1)
memory usage: 3.4 KB
差分涉及从时间序列本身减去滞后版本。在季节差异的情况下,您可以从上一年的同一季节中减去该值。
当您采用第一个季节差异时,您会丢失前 12 个数据点(因为没有前一年前 12 个月的数据)。这会导致生成的差分序列中出现缺失值。
df['#Passengers_diff'].fillna(method='backfill', inplace=True)<class 'pandas.core.frame.DataFrame'>
DatetimeIndex: 144 entries, 1949-01-01 to 1960-12-01
Data columns (total 2 columns):# Column Non-Null Count Dtype
--- ------ -------------- ----- 0 #Passengers 144 non-null int64 1 #Passengers_diff 144 non-null float64
dtypes: float64(1), int64(1)
memory usage: 3.4 KB
识别季节性因素
result = seasonal_decompose(df['#Passengers'], model='multiplicative', period=12)
trend = result.trend.dropna()
seasonal = result.seasonal.dropna()
residual = result.resid.dropna()plt.figure(figsize=(6,6))plt.subplot(4, 1, 1)
plt.plot(df['#Passengers'], label='Original Series')
plt.legend()plt.subplot(4, 1, 2)
plt.plot(trend, label='Trend')
plt.legend()plt.subplot(4, 1, 3)
plt.plot(seasonal, label='Seasonal')
plt.legend()plt.subplot(4, 1, 4)
plt.plot(residual, label='Residuals')
plt.legend()plt.tight_layout()
plt.show()外生变量
df['month_index'] = df.index.month模型拟合
SARIMAX_model = pm.auto_arima(df[['#Passengers']], exogenous=df[['month_index']],start_p=1, start_q=1,test='adf',max_p=3, max_q=3, m=12,start_P=0, seasonal=True,d=None, D=1,trace=False,error_action='ignore',suppress_warnings=True,stepwise=True)模型预测函数
def sarimax_forecast(SARIMAX_model, periods=24):# Forecastn_periods = periodsforecast_df = pd.DataFrame({"month_index": pd.date_range(df.index[-1], periods=n_periods, freq='MS').month},index=pd.date_range(df.index[-1] + pd.DateOffset(months=1), periods=n_periods, freq='MS'))fitted, confint = SARIMAX_model.predict(n_periods=n_periods,return_conf_int=True,exogenous=forecast_df[['month_index']])index_of_fc = pd.date_range(df.index[-1] + pd.DateOffset(months=1), periods=n_periods, freq='MS')# make series for plotting purposefitted_series = pd.Series(fitted, index=index_of_fc)lower_series = pd.Series(confint[:, 0], index=index_of_fc)upper_series = pd.Series(confint[:, 1], index=index_of_fc)# Plotplt.figure(figsize=(15, 7))plt.plot(df["#Passengers"], color='#1f76b4')plt.plot(fitted_series, color='darkgreen')plt.fill_between(lower_series.index,lower_series,upper_series,color='k', alpha=.15)plt.title("SARIMAX - Forecast of Airline Passengers")plt.show()sarimax_forecast(SARIMAX_model, periods=24)
其中,绘图阴影区域表示预测值周围的置信区间。
👉参阅一:计算思维
👉参阅二:亚图跨际
相关文章:

Python | C++ | MATLAB | Julia | R 市场流动性数学预期评估量
🎯要点 🎯市场流动性策略代码应用:🎯动量策略:滚动窗口均值策略、简单移动平均线策略、指数加权移动平均线策略、相对强弱指数、移动平均线收敛散度交叉策略、三重指数平均策略、威廉姆斯 %R 策略 | 🎯均值…...

Android 常用开源库 MMKV 源码分析与理解
文章目录 前言一、MMKV简介1.mmap2.protobuf 二、MMKV 源码详解1.MMKV初始化2.MMKV对象获取3.文件摘要的映射4.loadFromFile 从文件加载数据5.数据写入6.内存重整7.数据读取8.数据删除9.文件回写10.Protobuf 实现1.序列化2.反序列化 12.文件锁1.加锁2.解锁 13.状态同步 总结参考…...
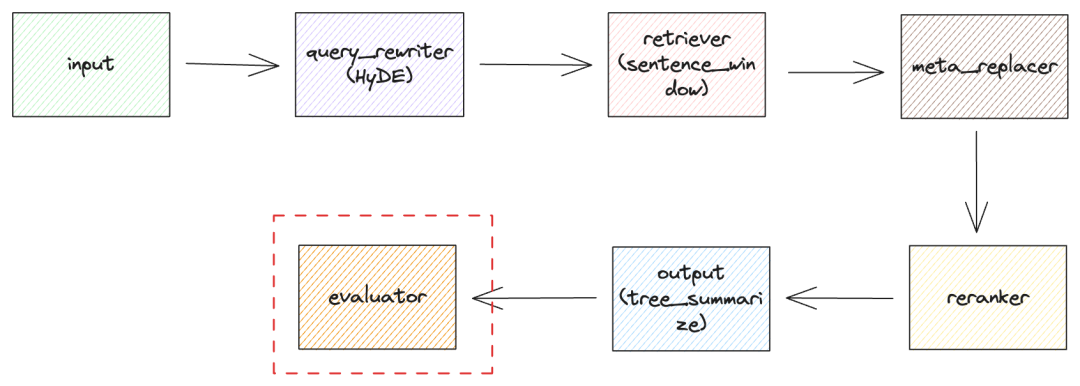
大模型高级 RAG 检索策略之流程与模块化
我们介绍了很多关于高级 RAG(Retrieval Augmented Generation)的检索策略,每一种策略就像是机器中的零部件,我们可以通过对这些零部件进行不同的组合,来实现不同的 RAG 功能,从而满足不同的需求。 今天我们…...

TCPListen客户端和TCPListen服务器
创建项目 TCPListen服务器 public Form1() {InitializeComponent();//TcpListener 搭建tcp服务器的类,基于socket套接字通信的//1创建服务器对象TcpListener server new TcpListener(IPAddress.Parse("192.168.107.83"), 3000);//2 开启服务器 设置最大…...

DDei在线设计器-属性编辑器
DDei-Core-属性编辑器 DDei-Core-属性编辑器插件包含了文本、大文本、数值、下拉、单选、勾选以及颜色等属性编辑。 图形和属性共同构成一个完整的定义,属性编辑器就是编辑属性值的控件。当选中图形实例时,属性面板就会展现当前实例的所有属性以及属性编…...

八字综合测算网整站源码程序/黄历/灵签/排盘/算命/生肖星座/日历网/周公解梦
八字综合测算网整站源码程序/黄历/灵签/排盘/算命/生肖星座/日历网/周公解梦 演示地址: https://s24.gvyun.com/ 手机端地址: https://ms24.gvyun.com/ 网站功能分类: 八字:八字测算;日干论命;称骨论命…...
—— 布局管理)
C# WPF入门学习主线篇(十一)—— 布局管理
C# WPF入门学习主线篇(十一)—— 布局管理 欢迎来到C# WPF入门学习系列的第十一篇。在前面的文章中,我们已经探讨了WPF中的许多控件及其属性和事件。今天,我们将开启一个新的篇章——布局管理。布局管理是WPF中一个至关重要的概念…...

LabVIEW轴承试验机测控系统
开发了一种基于LabVIEW软件开发的大功率风电机组增速箱轴承试验机测控系统。系统主要用于模拟实际工况,进行轴承可靠性分析,以优化风电机组的性能和可靠性。通过高度自动化的测控系统,实现了对试验机的精确控制,包括速度、振动、温…...
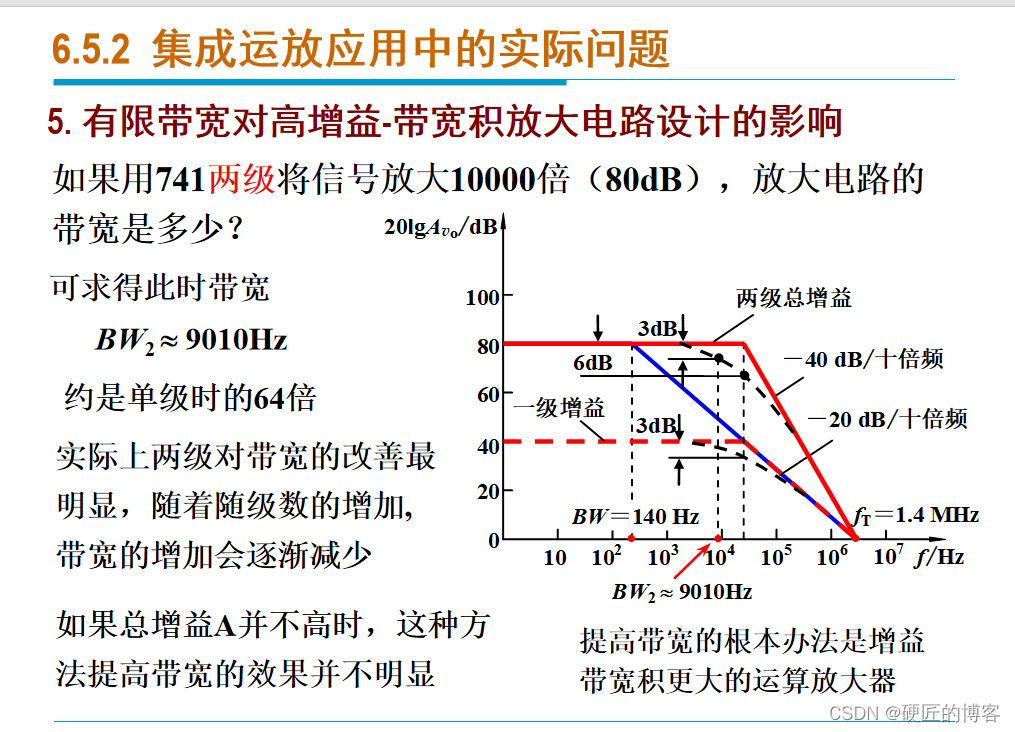
0605 实际集成运算放大器的主要参数和对应用电路的影响
6.5.1 实际集成运放的主要参数 6.5.2 集成运放应用中的实际问题 6.5.2 集成运放应用中的实际问题...
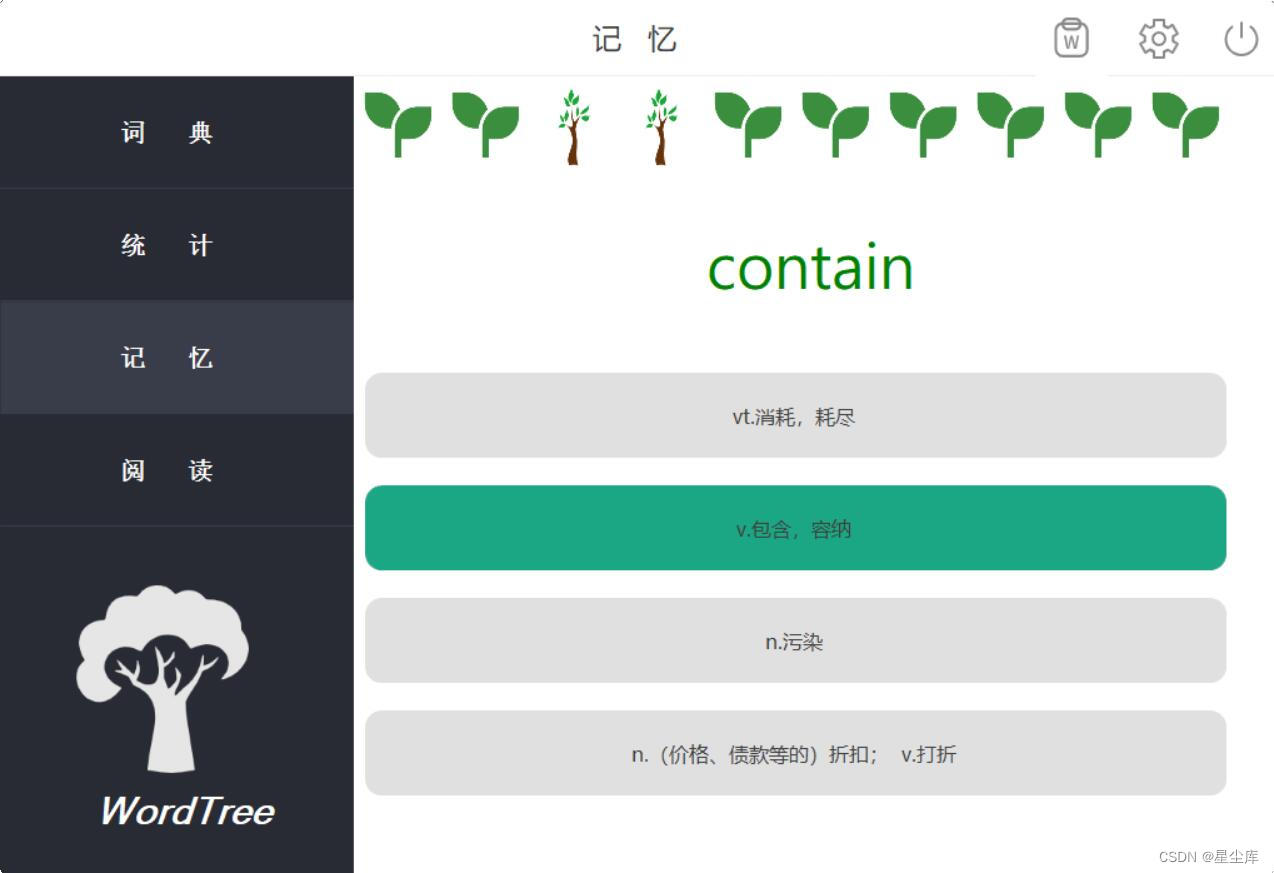
艾宾浩斯winform单词系统+mysql
为用户提供集词典、题库、记忆单词功能于一体的应用,为用户提供目的性强、科学高效、多样化的记忆单词方法,使用户学习英语和记忆单词的效率得到提高 单词记忆模块 管理模块 查询单词 阅读英文 查看词汇 记忆单词 收藏单词 字段管理设置 统计 艾宾浩斯wi…...

rv1126-rv1109-串口显示路径不变化
串口只有#, 后来看了教程改成如下 但是没有变化,那个路径都只显示rootLonbon# 于是最后改成了这样 因为:...

基于C#开发web网页管理系统模板流程-主界面密码维护功能完善
点击返回目录-> 基于C#开发web网页管理系统模板流程-总集篇-CSDN博客 前言 紧接上篇->基于C#开发web网页管理系统模板流程-主界面统计功能完善-CSDN博客 一个合格的管理系统,至少一定存在一个功能——用户能够自己修改密码,理论上来说密码只能有用…...

[NOVATEK] NT96580行车记录仪功能学习笔记(持续更新~
sdk文件结构(我个人理解) 1、DX文件夹里面是IO口以及项目使用到的相关外设配置 2、GX是外设功能实现函数所在文件夹 3、Startup文件夹是整个项目的入口,里面有个startup.c文件是main函数所在 4、UIAPP是手机APP功能设置的文件夹,增删改功能主要是在UIAPP和UIWnd文件夹里…...

力扣752. 打开转盘锁
Problem: 752. 打开转盘锁 文章目录 题目描述思路及解法复杂度Code 题目描述 思路及解法 1.用一个集合 deads 存储所有的“死锁”状态,一个集合 visited 存储所有已经访问过的状态,以避免重复访问,一个队列 q 进行广度优先搜索(BF…...

揭秘:义乌理阳的跨境选品师项目
在全球经济一体化的今天,跨境电商已成为各国贸易的重要组成部分,而选品师作为其中的关键角色,扮演着挑选优质商品的重要角色。在中国义乌,一家名为理阳信息咨询服务有限公司备受关注,因其据称拥有跨境选品师项目而备受…...

电视剧推荐
1、《春色寄情人》 2、《唐朝诡事录》 3、《南来北往》 4、《与凤行》 5、《利剑玫瑰》 6、《承欢记》...

ISO 19115-3:2023 关于元数据最小实例的允许命名空间的详细说明
理解说明内容 标识符(Identifier) URL: https://standards.isotc211.org/19115/-1/1/req/metadata-minimal-xml/allowed-namespaces解释: 这个 URL 标识了元数据最小实例中允许的命名空间的具体标准和规范。包含于(Included in) 要求类 4:元数据信息最小交换 (ISO 19115-…...
最新下载:CorelDraw 2023【软件附加安装教程】
简介: CorelDRAW Graphics Suite 订阅版拥有配备齐全的专业设计工具包,可以通过非常高的效率提供令人惊艳的矢量插图、布局、照片编辑和排版项目。价格实惠的订阅就能获得令人难以置信的持续价值,即时、有保障地获得独家的新功能和内容、一流…...
QT系列教程(8) QT 布局学习
简介 Qt 中的布局有三种方式,水平布局,垂直布局,栅格布局。 通过ui设置布局 我们先创建一个窗口应用程序,程序名叫layout,基类选择QMainWindow。但我们不使用这个mainwindow,我们创建一个Qt应用程序类Log…...
SpringCloud Gateway中Route Predicate Factories详细说明
官网地址:https://cloud.spring.io/spring-cloud-static/spring-cloud-gateway/2.2.1.RELEASE/reference/html/#gateway-request-predicates-factories Spring Cloud Gateway将路由匹配作为Spring WebFlux HandlerMapping基础架构的一部分。 Spring Cloud Gateway …...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...
