第十五届蓝桥杯大赛 国赛 pb组F题【括号与字母】(15分) 栈的应用
- 博客主页:誓则盟约
- 系列专栏:IT竞赛 专栏
- 关注博主,后期持续更新系列文章
- 如果有错误感谢请大家批评指出,及时修改
- 感谢大家点赞👍收藏⭐评论✍



试题F:括号与字母
【问题描述】
给定一个仅包含小写字母和括号的字符串 S ,保证括号可以两两匹配。 给出 Q 组询问,每组询问给出一个小写字母 ci 和一个数 xi ,询问 S 中有 多少对匹配的括号之间有不少于 xi 个 ci 。
【输入格式】
输入的第一行包含一个字符串 S 。 第二行包含一个整数 Q 。 接下来 Q 行,每行包含一个小写字母 ci 和一个整数 xi 表示一组询问,用 一个空格分隔。
【输出格式】
输出 Q 行,每行包含一个整数,依次表示每个询问的答案。
【样例输入】
((a)()((b)((c))))
3
a 2
b 1
c 1
【样例输出】
0
3
4
【评测用例规模与约定】
对于 40% 的评测用例,|S |, Q ≤ 5000 ; 对于 70% 的评测用例,|S | ≤ 100000 ; 对于所有评测用例,1 ≤ |S | ≤ 106 ,1 ≤ Q ≤ 100000 ,0 ≤ xi < 106 。其中 |S | 表示 S 的长度。
分析问题:
仔细读题,保证给的s中括号都两两匹配,那么这道题就相当于是在考察入栈和出栈的问题了,这里我们需要定义一个符号栈和一个字母栈。
- 符号栈:专门用来存储左括号,遇见左括号则入栈,遇见右括号则栈顶的左括号出栈。并且对加入的左括号所包含的字母个数做标记,记录出栈前的左括号和右括号之间有几个字母,最后可以通过字符串切割来找到这个括号内的字母。
- 字母栈:遇见字母则入栈,不需要出栈。用于储存字母。
代码实现:
s=str(input()) # 输入s
s0="abcdefghijklmnopqrstuvwxyz" # 一会判断字母要用
q=int(input()) # 输入询问次数q
for i in range(q): # q次循环,每次询问都有一个输出值s1,b1=map(str,input().split()) # 输入要询问的字母和被包括的个数b=int(b1) # 转次数为int型v=s.count(s1) if v<b:print(0) # 此时总个数都小于要询问的个数b,一定没有符合题意的 返回0else:re=0 # 记录个数stick_1=[] # 符号栈stick_2=[] # 字母栈for j in s: # 遍历sif j=="(": #遇见左括号则入栈stick_1.append([j,0]) # 后面的0 用于标记这个左括号与对应的右括号之间有几个字母elif j in s0: # 如果是字母,则入字母栈stick_2.append(j)for w in range(len(stick_1)): stick_1[w][-1]+=1 # 对于所有的左括号对应的标记值,都加1,说明他们与对应的右括号之间多了一个字母else: # 否则则是右括号k_1,st=stick_1.pop() # 遇见右括号,则从符号栈出栈一个左括号if st==0: continue # 说明左括号右括号之间没有元素,直接跳ve=stick_2[-1:-st-1:-1] # 否则说明之间有元素,则找到这些元素if ve.count(s1)>=b:# 判断ve中要查询的字母个数是否合题意re+=1 # 标记的个数+1print(re) # 对于每次询问都返回 res
总结:
以下是对这段代码的详细解释:
s = str(input()):获取用户输入的字符串s。s0 = "abcdefghijklmnopqrstuvwxyz":定义了所有小写字母的字符串,用于后续判断字母。q = int(input()):获取询问的次数。- 然后进入
q次循环:s1, b1 = map(str, input().split()):分别获取要询问的字母和期望的包含个数,将b1转换为整数类型。v = s.count(s1):计算字符串s中该字母出现的总次数。如果总次数小于期望个数,直接输出0。- 否则,进行复杂的处理:
re = 0用于记录符合条件的个数。stick_1是符号栈,stick_2是字母栈。- 遍历字符串
s:- 遇到左括号,将其及初始标记值
0入栈。 - 遇到字母,入字母栈,并更新符号栈中每个左括号对应的标记值,表示它们之间多了一个字母。
- 遇到右括号,弹出符号栈中的一个左括号和标记值。如果标记值为
0,则直接跳过;否则,找到左括号和右括号之间的元素,判断其中要查询的字母个数是否满足条件,如果满足则增加标记个数re。
- 遇到左括号,将其及初始标记值
- 最后输出每次询问对应的
re。
总的来说,这段代码主要是通过栈的操作来处理字符串中括号内的子串,并判断其中特定字母的出现次数是否满足要求。
对于这道题的考点和反思如下:
考查内容:
- 对字符串的处理和操作能力,包括字符的统计、遍历等。
- 栈这种数据结构的运用,通过栈来处理括号内的内容和计数。
- 逻辑思维和问题分析解决能力,需要仔细思考如何在复杂的条件下准确判断符合要求的情况。
学会的内容:
- 更加深入地掌握了字符串处理的技巧和方法。
- 熟悉了栈的实际应用场景,以及如何通过栈来解决特定问题。
- 提升了面对复杂逻辑问题时设计算法和代码实现的能力。
反思:
- 在处理复杂逻辑时,要更加仔细地设计算法和流程,避免遗漏特殊情况。
- 对于数据结构的运用要更加灵活,根据具体问题选择合适的数据结构来优化解决方案。
- 编写代码时要注意代码的可读性和可维护性,以便后续的理解和修改。同时要充分考虑代码的效率和性能。
总之,这道题放在15分的位置,并不算是难题,主要还是考察对栈的应用熟练程度是否到位。 相关栈的篇章:栈的理解与应用

“甲之蜜糖,乙之砒霜。” ——《曼陀罗》
相关文章:

第十五届蓝桥杯大赛 国赛 pb组F题【括号与字母】(15分) 栈的应用
博客主页:誓则盟约系列专栏:IT竞赛 专栏关注博主,后期持续更新系列文章如果有错误感谢请大家批评指出,及时修改感谢大家点赞👍收藏⭐评论✍ 试题F:括号与字母 【问题描述】 给定一个仅包含小写字母和括号的字符串 S …...
)
MYSQL 三、mysql基础知识 4(存储过程与函数)
MySQL从5.0版本开始支持存储过程和函数。存储过程和函数能够将复杂的SQL逻辑封装在一起,应用程序无须关注存储过程和函数内部复杂的SQL逻辑,而只需要简单地调用存储过程和函数即可。 一、存储过程概述: 1.1理解: 含义&am…...

鸿蒙开发文件管理:【@ohos.statfs (statfs)】
statfs 该模块提供文件系统相关存储信息的功能,向应用程序提供获取文件系统总字节数、空闲字节数的JS接口。 说明: 本模块首批接口从API version 8开始支持。后续版本的新增接口,采用上角标单独标记接口的起始版本。 导入模块 import stat…...

C++和C语言到底有什么区别?
引言:C和C语言是两种非常常见的编程语言,由于其广泛的应用和灵活性,它们在计算机科学领域内受到了广泛的关注。虽然C是从C语言发展而来的,但是这两种语言在许多方面都有所不同。本文将对C和C语言进行比较和分析,以便更…...
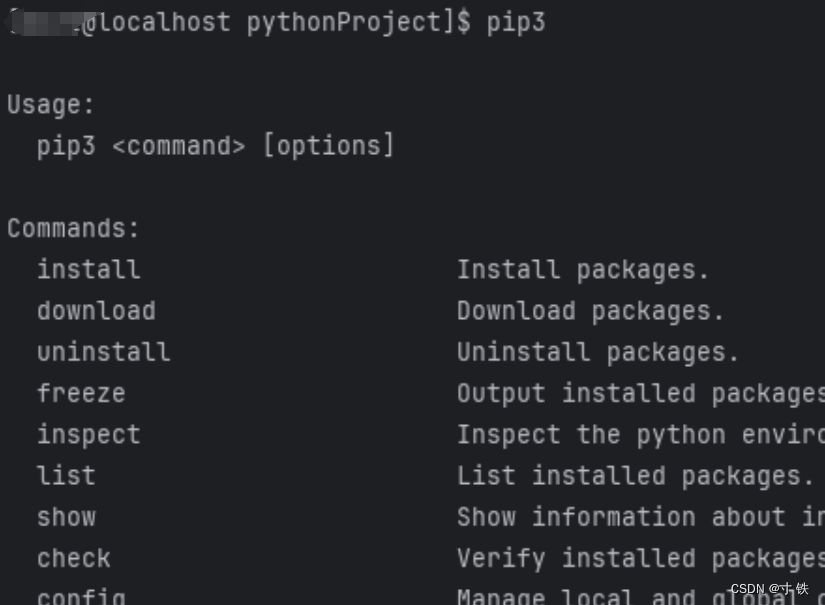
【Centos】深度解析:CentOS下安装pip的完整指南
【Centos】深度解析:CentOS下安装pip的完整指南 大家好 我是寸铁👊 总结了一篇【Centos】深度解析:CentOS下安装pip的完整指南✨ 喜欢的小伙伴可以点点关注 💝 方式1(推荐) 下载get-pip.py到本地 sudo wget https://bootstrap.p…...

半导体PW和NPW的一些小知识
芯片制造厂内的晶圆主要由两种,生产晶圆(PW:Product Wafer)和非生产晶圆(NPW:None Product Wafer)。 一、生产晶圆(PW) 生产晶圆的一些关键特点: 高纯度硅材料:生产晶…...
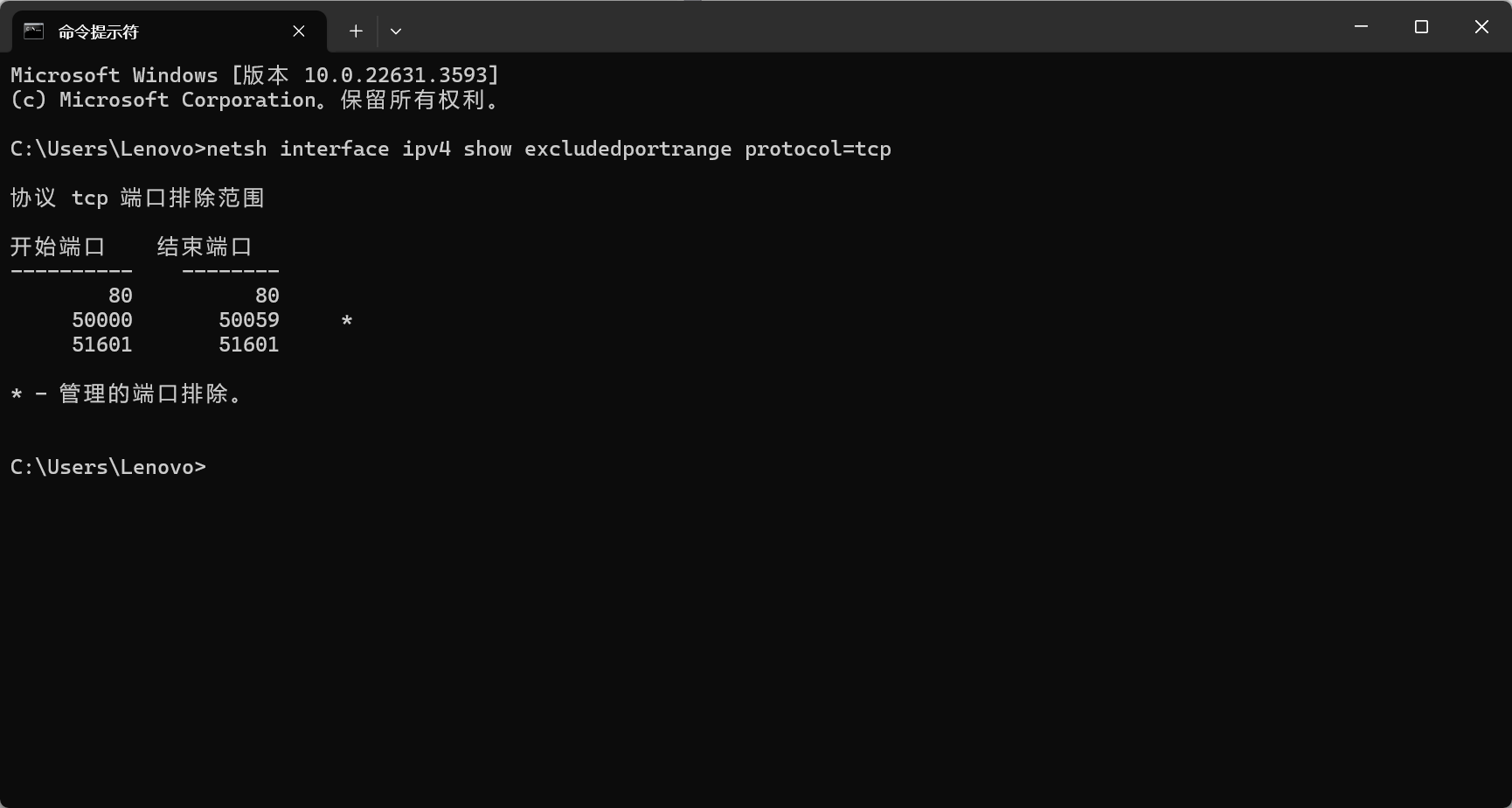
后端启动项目端口冲突问题解决
后端启动项目端口冲突 原因: Vindows Hyper-V虚拟化平台占用了端口。 解决方案一: 查看被占用的端口范围,然后选择一个没被占用的端口启动项目。netsh interface ipv4 show excludedportrange protocoltcp 解决方案二: 禁用H…...

【优选算法】优先级队列 {优先级队列解决TopK问题,利用大小堆维护数据流的中位数}
一、经验总结 优先级队列(堆),常用于在集合中筛选最值或解决TopK问题。 提示:对于固定序列的TopK问题,最优解决方案是快速选择算法,时间复杂度为O(N)比堆算法O(NlogK)更优;而对于动态维护数据流…...
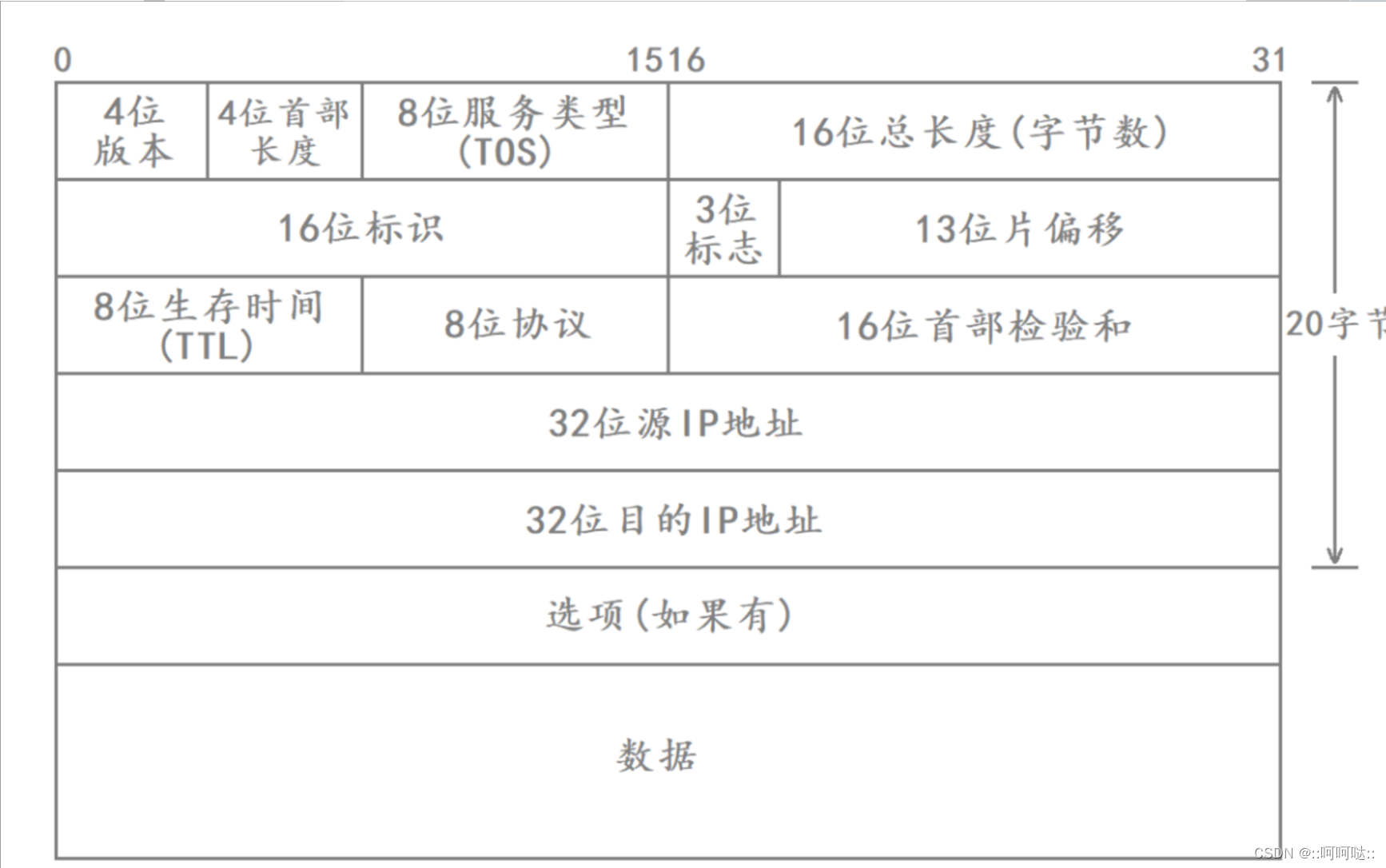
11 IP协议 - IP协议头部
什么是 IP 协议 IP(Internet Protocol)是一种网络通信协议,它是互联网的核心协议之一,负责在计算机网络中路由数据包,使数据能够在不同设备之间进行有效的传输。IP协议的主要作用包括寻址、分组、路由和转发数据包&am…...

【java】【python】leetcode刷题记录--二叉树
144.二叉树的前序遍历 题目链接 前、中、后的遍历的递归做法实际上都是一样的,区别就是遍历操作的位置不同。 对于先序遍历,也就是先根,即把查看当前结点的操作放在最前面即可。 class Solution {public List<Integer> preorderTrav…...
EVA-CLIP实战
摘要 EVA-CLIP,这是一种基于对比语言图像预训练(CLIP)技术改进的模型,通过引入新的表示学习、优化和增强技术,显著提高了CLIP的训练效率和效果。EVA-CLIP系列模型在保持较低训练成本的同时,实现了与先前具有相似参数数量的CLIP模型相比更高的性能。特别地,文中提到的EV…...

限定法术施放目标
实现目标 法术只对特定 creature | gameobject 施放,否则无法施放 实现方法 conditions SourceTypeOrReferenceId:13(CONDITION_SOURCE_TYPE_SPELL_IMPLICIT_TARGET)SourceGroup:受条件影响的法术效果掩码…...

【通信原理】数字频带传输系统
二进制数字调制,解调原理:2ASK,2FSK 二进制数字调制,解调原理:2PSK,2DPSK 二进制数字已调制信号的功率谱 二进制数字调制系统的抗噪声性能 二进制调制系统的性能总结...
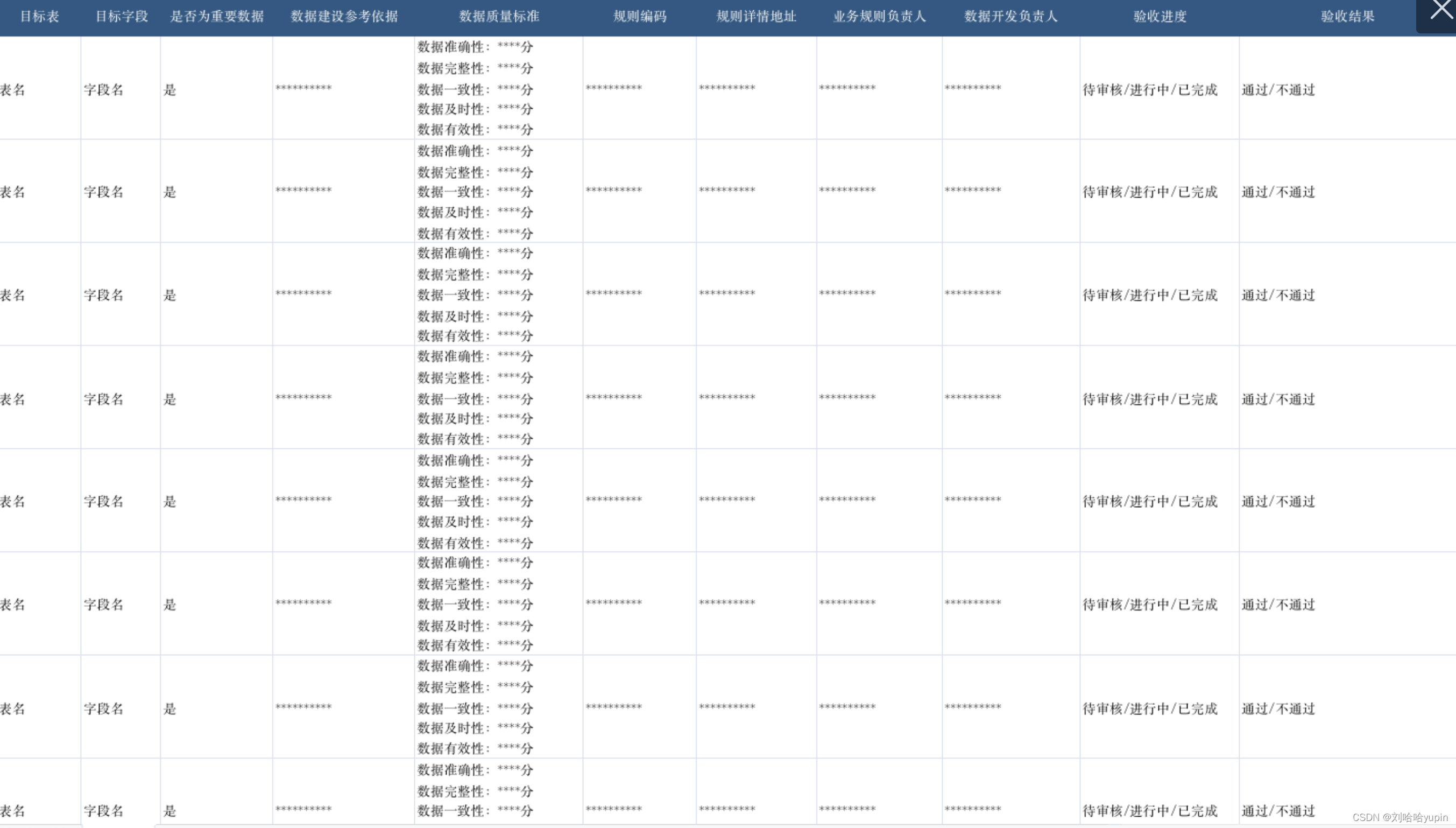
数据价值管理-数据验收标准
前情提要:数据价值管理是指通过一系列管理策略和技术手段,帮助企业把庞大的、无序的、低价值的数据资源转变为高价值密度的数据资产的过程,即数据治理和价值变现。第一讲介绍了业务架构设计的基本逻辑和思路。前面我们讲完了数据资产建设标准…...

vue3模板语法总结
1. 响应式数据 Vue 3中的数据是响应式的,即当数据发生变化时,视图会自动更新。这是通过使用JavaScript的getter和setter来实现的。 2. 组件化 Vue 3采用组件化开发方式,允许创建可复用的组件。 每个组件都有自己的作用域,并且…...
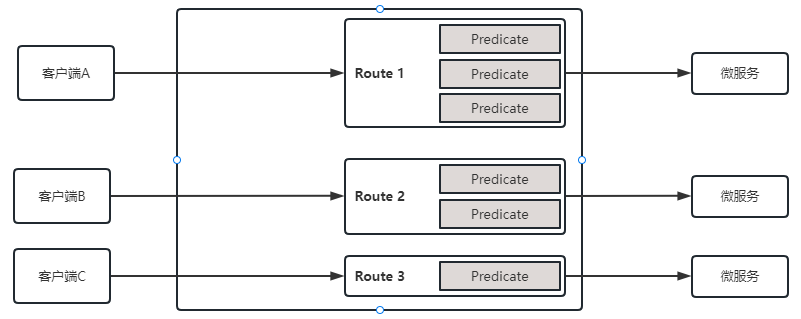
Spring Cloud 之 GateWay
前言 前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家:https://www.captainbed.cn/z ChatGPT体验地址 文章目录 前言前言1、通过API网关访问服务2、Spring Cloud GateWay 最主要的功能就是路由…...

可转债全部历史因子数据,提供api支持
今天在写可转债系统,顺便下载了一下服务器的可转债数据,给大家研究使用 from trader_tool.stock_data import stock_datafrom trader_tool.lude_data_api import lude_data_apiimport osclass convertible_bond_back_test_system: 可转债回测系统…...

Python | C++ | MATLAB | Julia | R 市场流动性数学预期评估量
🎯要点 🎯市场流动性策略代码应用:🎯动量策略:滚动窗口均值策略、简单移动平均线策略、指数加权移动平均线策略、相对强弱指数、移动平均线收敛散度交叉策略、三重指数平均策略、威廉姆斯 %R 策略 | 🎯均值…...

Android 常用开源库 MMKV 源码分析与理解
文章目录 前言一、MMKV简介1.mmap2.protobuf 二、MMKV 源码详解1.MMKV初始化2.MMKV对象获取3.文件摘要的映射4.loadFromFile 从文件加载数据5.数据写入6.内存重整7.数据读取8.数据删除9.文件回写10.Protobuf 实现1.序列化2.反序列化 12.文件锁1.加锁2.解锁 13.状态同步 总结参考…...
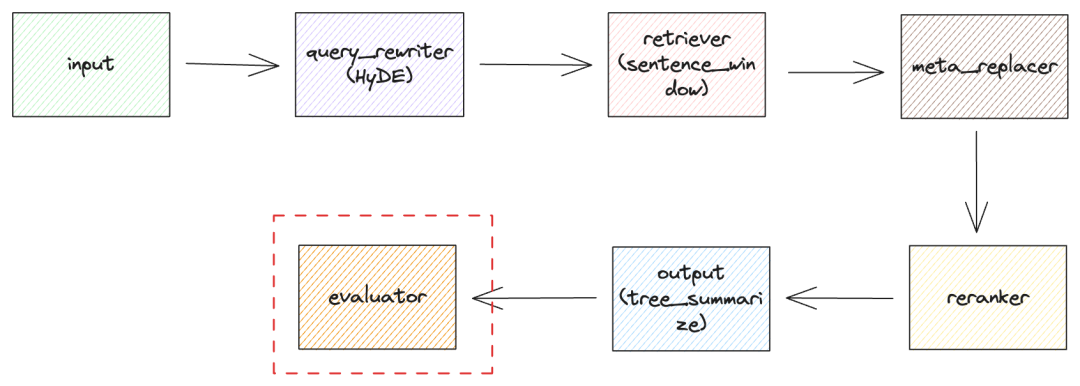
大模型高级 RAG 检索策略之流程与模块化
我们介绍了很多关于高级 RAG(Retrieval Augmented Generation)的检索策略,每一种策略就像是机器中的零部件,我们可以通过对这些零部件进行不同的组合,来实现不同的 RAG 功能,从而满足不同的需求。 今天我们…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...
提供了哪些便利?)
现有的 Redis 分布式锁库(如 Redisson)提供了哪些便利?
现有的 Redis 分布式锁库(如 Redisson)相比于开发者自己基于 Redis 命令(如 SETNX, EXPIRE, DEL)手动实现分布式锁,提供了巨大的便利性和健壮性。主要体现在以下几个方面: 原子性保证 (Atomicity)ÿ…...

wpf在image控件上快速显示内存图像
wpf在image控件上快速显示内存图像https://www.cnblogs.com/haodafeng/p/10431387.html 如果你在寻找能够快速在image控件刷新大图像(比如分辨率3000*3000的图像)的办法,尤其是想把内存中的裸数据(只有图像的数据,不包…...

一些实用的chrome扩展0x01
简介 浏览器扩展程序有助于自动化任务、查找隐藏的漏洞、隐藏自身痕迹。以下列出了一些必备扩展程序,无论是测试应用程序、搜寻漏洞还是收集情报,它们都能提升工作流程。 FoxyProxy 代理管理工具,此扩展简化了使用代理(如 Burp…...
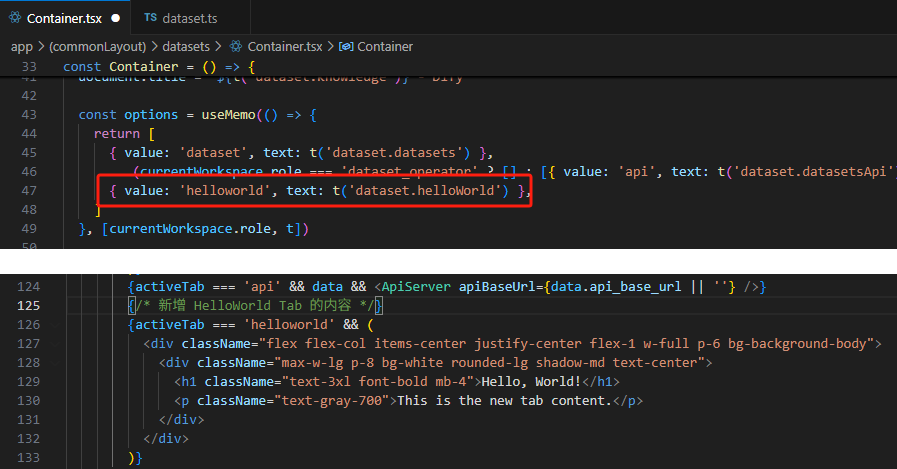
【技巧】dify前端源代码修改第一弹-增加tab页
回到目录 【技巧】dify前端源代码修改第一弹-增加tab页 尝试修改dify的前端源代码,在知识库增加一个tab页"HELLO WORLD",完成后的效果如下 [gif01] 1. 前端代码进入调试模式 参考 【部署】win10的wsl环境下启动dify的web前端服务 启动调试…...
