函数递归(C语言)(详细过程!)
函数递归
- 一. 递归是什么
- 1.1 递归的思想
- 1.2 递归的限制条件
- 二. 递归举例
- 2.1 求n的阶乘
- 2.2 按顺序打印一个整数的每一位
- 三. 递归与迭代
- 3.1 求第n个斐波那契数
一. 递归是什么
递归是学习C语言很重要的一个知识,递归就是函数自己调用自己,是一种解决问题的方法,下面就使用一个简单的代码帮助大家理解:下面展示一些 内联代码片。
#include <stdio.h>
int main()
{
printf("hehe\n");
main() //出现了main函数自己调用自己
return 0;

上图展示的代码就是一个简单的调用函数的例子,不断的调用main函数也就是要不断输出hehe,形成了一个循环,这就是一个简单的函数递归。
1.1 递归的思想
把一个大型问题转换成一个与原问题相似但是规模较小的子问题来解决,直到到子问题不能再被拆分,递归就结束了。递归中的递就是递推的意思,归就是回归的意思,下面会有详细的解释。
1.2 递归的限制条件
递归在书写的时候,有两个必要条件:
. 递归存在限制条件,当满足这个限制条件的时候,递归便不再继续
. 每次递归之后越来越接近这个限制条件
二. 递归举例
2.1 求n的阶乘
为了让大家更好理解递归是怎么回事,我们可以举几个例子,下面为大家展示第一个例子求n的阶乘的代码: 内联代码片。
int Fact(int n)
{if (n == 0)return 1;else if (n > 0)return n * Fact(n - 1);//相当于是多次调用这个函数,形成一个循环,不断地累乘
}int main()
{int n = 0;scanf("%d", &n);int r = Fact(n);printf("%d", r);return 0;
}
上述代码就给大家演示了一遍比较基本的函数递归,我们可以看到如果n大于0的话,就会返回n*Fact(n-1),所以就相当于不断的调用Fact函数,如果大家还是不太理解,下面我们用一张图帮助大家进一步理解:
2.2 按顺序打印一个整数的每一位
这是为大家展示的第二个例子,按顺序打印一个整数的每一位。首先我们看到这个题目,我们不难想到用%的方法,假如现在给一个数字1234,要如何打印出1 2 3 4 这四个数字呢?首先就是很容易想到1234%10=4,这时候我们就得到了4,然后1234/10=123(默认取整),然后再用123%10=3,这时候我们就得到了3…按照这个思路我们的代码就能实现,后面我还会再加上图片解释,方便大家进一步理解: 内联代码片。
void get(int n)
{if (n > 9){get(n / 10);}printf("%d ", n % 10);
}int main()
{int n = 0;scanf("%d", &n);get(n);return 0;
}

三. 递归与迭代
(1)递归是⼀种很好的编程技巧,但是和很多技巧⼀样,也是可能被误⽤的,就像举例1⼀样,看到推导的公式,很容易就被写成递归的形式,为大家解释一下,我们的第一个例子求n的阶乘,我们用递归的方法很容易算出来,但是我们可以自己操作一下,如果数值小的话,计算结果是很快出来,但是如果我们的数值偏大,假如我们输入50,那么计算结果就会很慢,原因就是 Fact函数是可以产生正确的结果,但是在递归函数调用的过程中涉及⼀些运行时的开销。
- 在C语言中每⼀次函数调用,都需要为本次函数调用在内存的栈区,申请⼀块内存空间来保存函数调用期间的各种局部变量的值,这块空间被称为运行时堆栈,或者函数栈帧。
- 函数不返回,函数对应的栈帧空间就⼀直占用,所以如果函数调用中存在递归调用的话,每⼀次递归函数调用都会开辟属于自己的栈帧空间,直到函数递归不再继续,开始回归,才逐层释放栈帧空间。所以如果采用函数递归的方式完成代码,递归层次太深,就会浪费太多的栈帧空间,也可能引起栈溢出(stackoverflow)的问题。
(2)所以如果不想使用递归,就得想其他的办法,通常就是迭代的方式(通常就是循环的方式)比如我们举的第一个例子计算n的阶乘,也是可以产⽣1~n的数字累计乘在⼀起的。

上述代码是能够完成任务,并且效率是比递归的方式更好的。事实上,我们看到的许多问题是以递归的形式进行解释的,这只是因为它比非递归的形式更加清晰,但是这些问题的迭代实现往往比递归实现效率更高。但是当⼀个问题非常复杂,难以使用迭代的方式实现时,此时递归实现的简洁性便可以补偿它所带来的运行时开销。所以我们不能说是递归更便捷还是迭代更便捷,我们更多的要去思考问题本身。
3.1 求第n个斐波那契数
我们也能举出更加极端的例⼦,就像计算第n个斐波那契数,是不适合使⽤递归求解的,但是斐波那契数 (1 1 2 3 5 8 13…前两个数相加) 的问题通过是使⽤递归的形式描述的,如下:
当我们n输⼊为50的时候,需要很长时间才能算出结果,这个计算所花费的时间,是我们很难接受的,这也说明递归的写法是非常低效的,那是为什么呢?其实递归程序会不断的展开,在展开的过程中,我们很容易就能发现,在递归的过程中会有重复计算,而且递归层次越深,冗余计算就会越多。
就像上面的图片上展示的,计算一个数值,就要将它拆分成另外两个数,以此类推,会循环很多很多次,也造成了巨大的计算量,所以在有些时候我们不妨试试另一种方法,例如迭代的方法,其实循环也算是迭代的一种,下图计算将递归的方法转换成迭代的方式去实现这个代码,效率就要高出很多了。有时候,递归虽好,但是也会引⼊⼀些问题,所以我们⼀定不要迷恋递归,适可而止就好。
以上就是关于递归的一些初级的理解,在后期我也会为大家继续写更多关于递归的知识,以及一些深入的了解。
相关文章:

函数递归(C语言)(详细过程!)
函数递归 一. 递归是什么1.1 递归的思想1.2 递归的限制条件 二. 递归举例2.1 求n的阶乘2.2 按顺序打印一个整数的每一位 三. 递归与迭代3.1 求第n个斐波那契数 一. 递归是什么 递归是学习C语言很重要的一个知识,递归就是函数自己调用自己,是一种解决问题…...

uniapp 接口请求封装
根目录下创建 config目录 api.js request.js // request.js // 封装一个通用的网络请求函数 适当调整 function httpRequest(options) {const userToken uni.getStorageSync(access_token).token;return new Promise((resolve, reject) > {uni.request({url: ${options.ur…...

C++中的观察者模式
目录 观察者模式(Observer Pattern) 实际应用 股票价格监控系统 发布-订阅系统 总结 观察者模式(Observer Pattern) 观察者模式是一种行为型设计模式,它定义了对象间的一对多依赖关系。当一个对象的状态发生改变…...
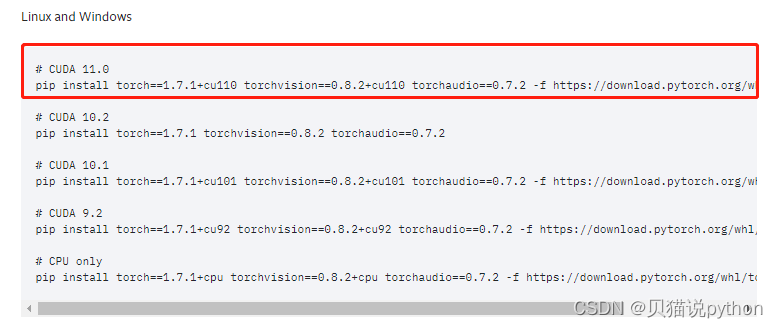
conda虚拟环境,安装pytorch cuda cudnn版本一致,最简单方式
1、pytorch版本安装(卸载也会有问题) (1)版本如何选择参考和卸载 https://zhuanlan.zhihu.com/p/401931724 (2)对应版本如何安装命令 https://pytorch.org/get-started/previous-versions/ 最简答安装参考…...
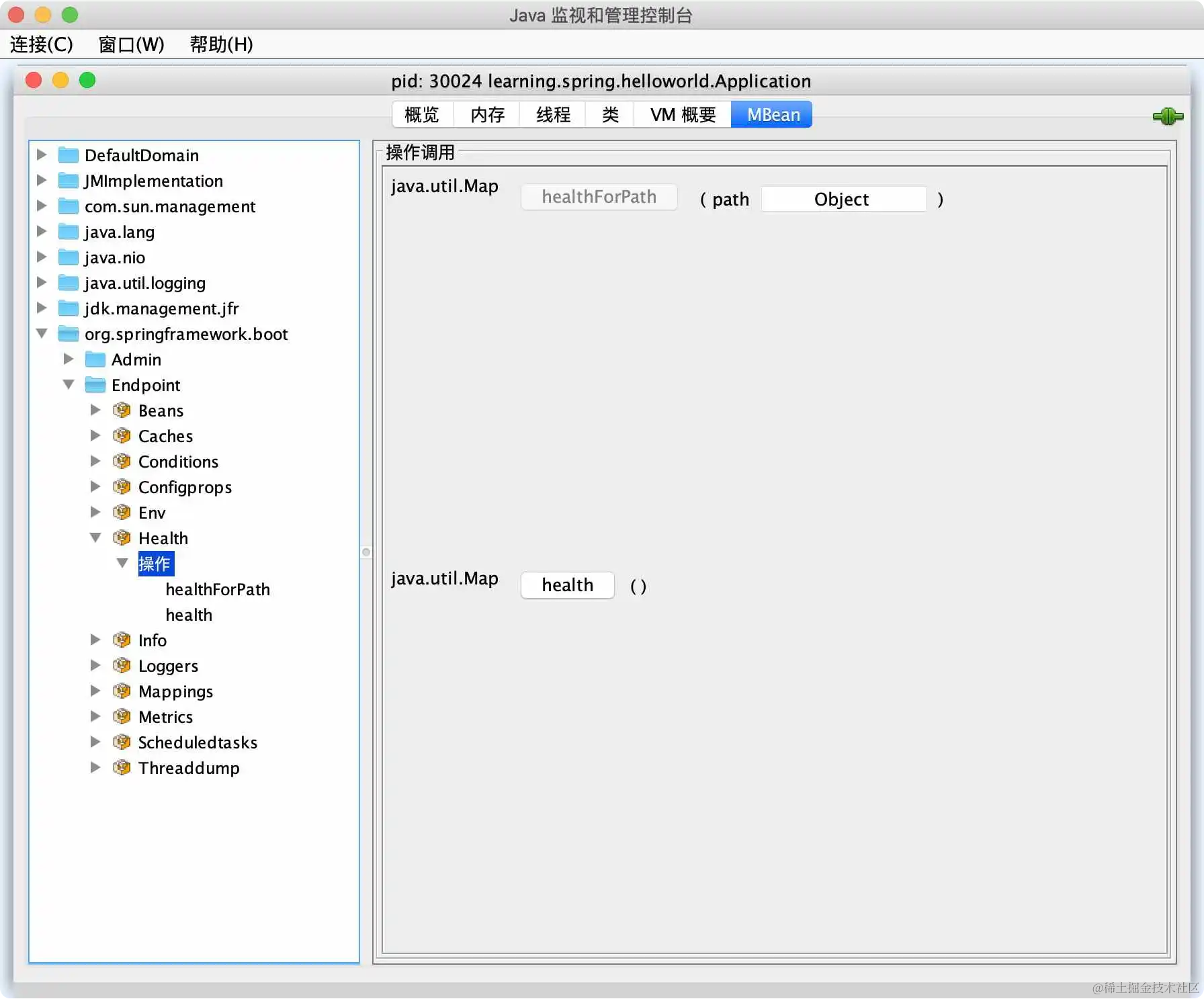
第 5 章:面向生产的 Spring Boot
在 4.1.2 节中,我们介绍了 Spring Boot 的四大核心组成部分,第 4 章主要介绍了其中的起步依赖与自动配置,本章将重点介绍 Spring Boot Actuator,包括如何通过 Actuator 提供的各种端点(endpoint)了解系统的…...

在 Windows 操作系统中,可以通过命令行工具来杀死进程
1. 使用 taskkill 命令 taskkill 命令是一个用于终止进程的命令行工具,可以通过进程名称或进程 ID (PID) 来杀死进程。 按进程名称杀死进程 taskkill /IM processname.exe /Fprocessname.exe 是进程的名称。/F 参数表示强制终止进程。 例如,终止名为…...

uni-app文件下载 h5 xls 乱码 锟斤拷 Blob pdf打不开
原先下载方式,PC管理端和浏览器打开文件能下载,xls没出现乱码,pdf能正常显示,H5下载xls乱码锟斤拷,PDF显示空白内容 怀疑是前端问题,也尝试过修改后端代码 后端设置编码格式 response.setCharacterEncoding(characte…...
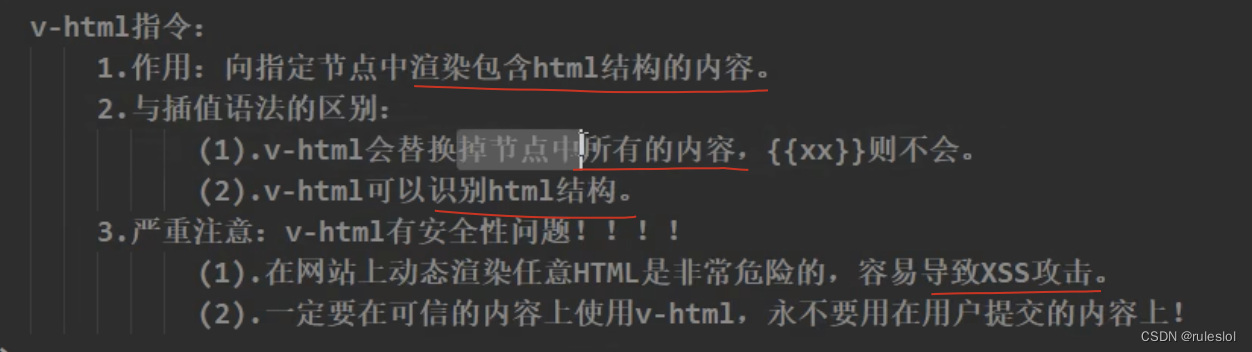
Vue25-内置指令02:v-text指令
一、v-html对比v-text v-html支持结构的解析,v-text不支持结构的解析。 二、v-html的安全性问题 2-1、cookie的原理(node.js) 7天免登录,cookie实现。 cookie的本质就是类似于json的字符串,格式是:key-va…...
stable diffusion中的negative prompt是如何工作的
https://stable-diffusion-art.com/how-negative-prompt-work/https://stable-diffusion-art.com/how-negative-prompt-work/https://zhuanlan.zhihu.com/p/644879268...

STM32项目分享:智能小区充电桩系统
目录 一、前言 二、项目简介 1.功能详解 2.主要器件 三、原理图设计 四、PCB硬件设计 1.PCB图 2.PCB板打样焊接图 五、程序设计 六、实验效果 七、资料内容 项目分享 一、前言 项目成品图片: 哔哩哔哩视频链接: https://www.bilibili.c…...

PDU模块中浪涌保护模块与空开模块的应用
由于PDU具体应用的特殊性,其在规划设计时具有应用场景的针对性,同时PDU的高度定制化的特点,是其他电气联接与保护产品所不具备的。 PDU基础的输出输入功能外,其电路的控制与电压保护器同时也极为重要。空气开关和浪涌保护器相关功…...
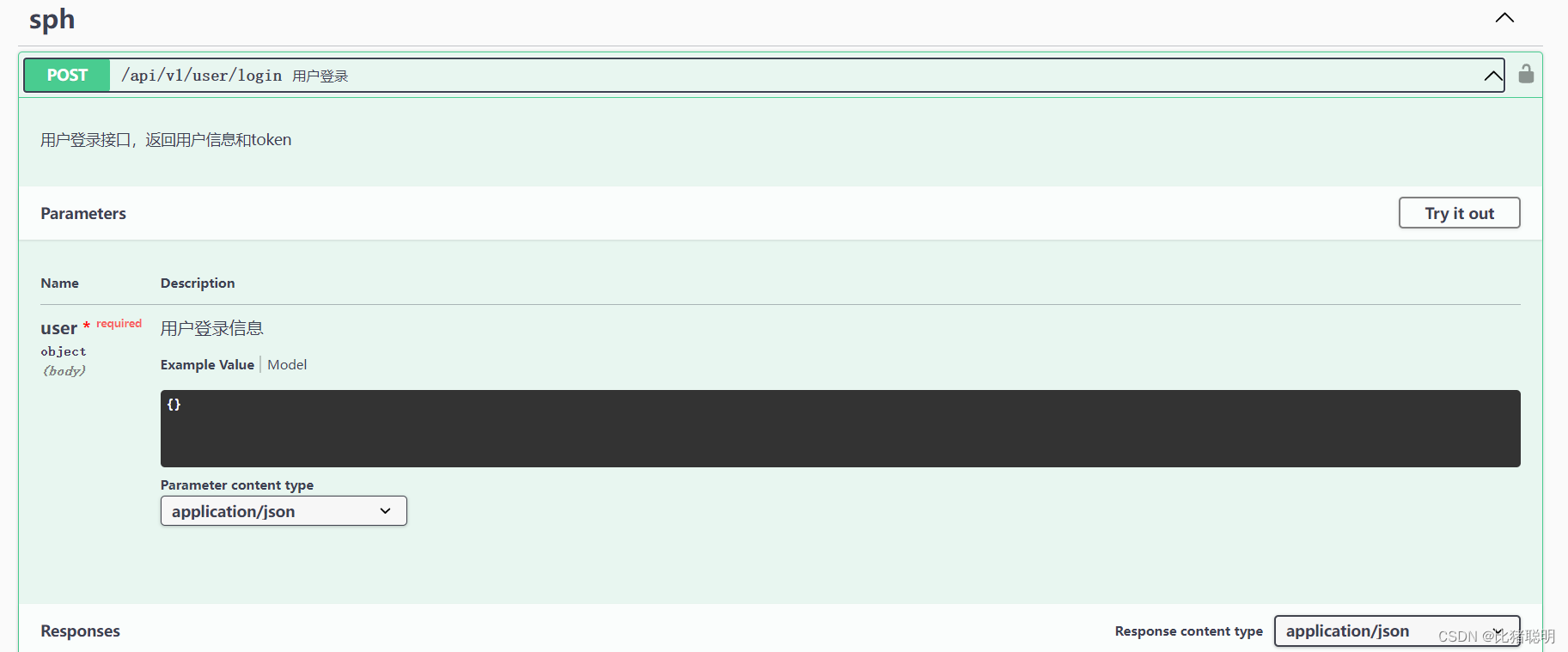
19、Go Gin框架集成Swagger
介绍: Swagger 支持在 Gin 路由中使用一系列注释来描述 API 的各个方面。以下是一些常用的 Swagger 注释属性,这些属性可以在 Gin 路由的注释中使用: Summary: 路由的简短摘要。Description: 路由的详细描述。Tags: 用于对路由进行分类的标…...
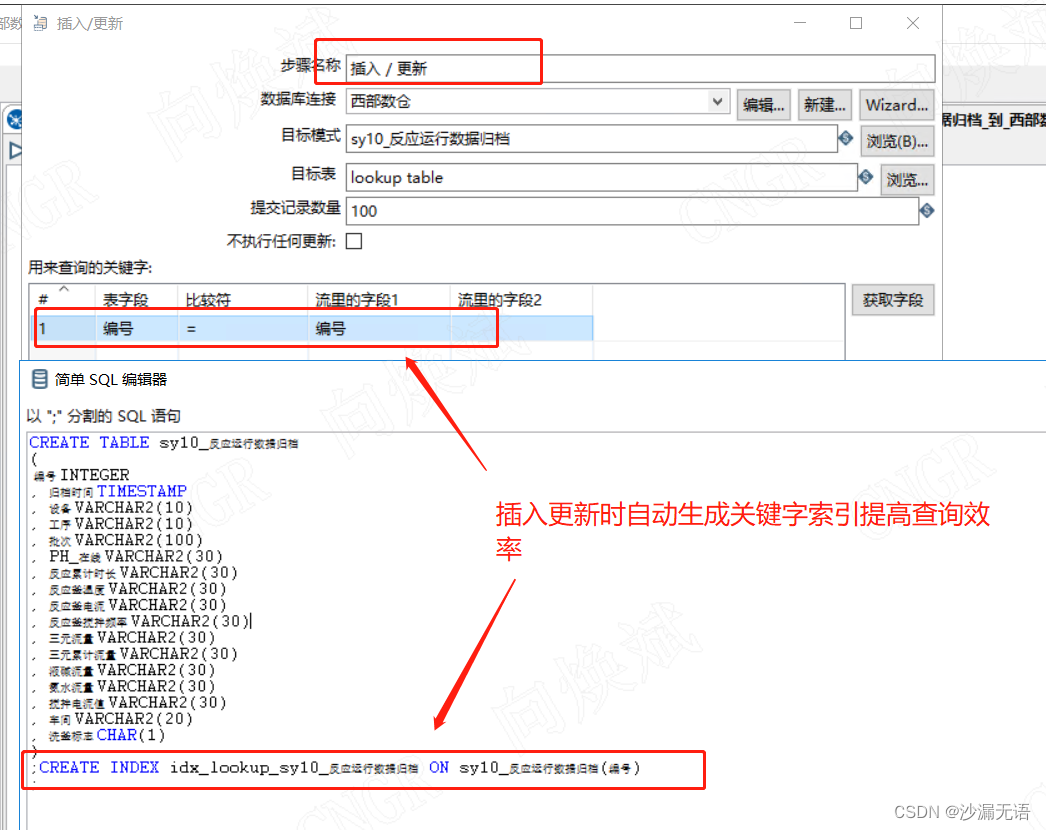
自动同步库数据——kettle开发36
kettle中的那些人工智能。 一、kettle的AI能力目录 跨库同步 2.自动开发 3.自动优化 二、AI实例 1、跨库同步 sqlsever表同步至oracle数据库 1.1源库sqlserver 1.2目标库oracle 1.3可视化跨库同步 使用多表复制向导 选择跨库的表,下一步下一步,即可…...

MSOCache在电脑中可以删除吗?
MSOCache文件夹在电脑中是可以删除的。但删除前需要了解以下几点: MSOCache文件夹的作用: MSOCache文件夹是Microsoft Office的本地安装源,用于存储Office安装和更新过程中所需的临时文件,如安装程序所需的组件、配置设置以及更新…...

数据网格和视图入门
WinForms数据网格(GridControl类)是一个数据感知控件,可以以各种格式(视图)显示数据。本主题包含以下部分,这些部分将指导您如何使用网格控件及其视图和列(字段)。 Grid Control’s…...

雨的轮回与生命的律动
雨的轮回与生命的律动 我们生活在一个充满变数的世界里,许多事情无法预测,如同这不知何时会停歇的雨。然而,尽管我们无法预知雨停的确切时刻,但我们深知,这场雨终将会过去,阳光终将再次洒满大地。这种对未…...
)
CANopen for Python 使用教程(二)
系列文章目录 前言 CANopen 标准的 Python 实现。该项目的目的是在一个简单的 Pythonic 接口中支持 CiA 301 标准中最常见的部分。它主要针对测试和自动化任务,而不是符合标准的主实施。 该库支持 Python 3.6 及以上版本。 一、特点 该库主要用作主库。 NMT 主站…...

前方碰撞缓解系统技术规范(简化版)
前方碰撞缓解系统技术规范(简化版) 1 系统概述2 工作时序3 预警目标4 功能条件5 HMI开关6 显示需求7 相关子功能8 TTC标定参考9 指标需求1 系统概述 前方碰撞缓解系统包含LW潜在危险报警、FCW前方碰撞预警和AEB自动紧急制动三个部分。 LW潜在危险报警:根据本车与前车保持的…...
——体系:数据收集——实施过程、应用特点)
数据赋能(117)——体系:数据收集——实施过程、应用特点
实施过程 数据收集过程是一个系统化、有序的步骤集合,旨在确保能够准确、高效地获取所需数据。以下是数据收集过程的基本步骤: 明确数据需求:这是数据收集的第一步,需要明确需要收集哪些类型的数据,这些数据将如何支…...

【吃包子game】
如果您想要编写一个简单的“吃包子”游戏代码,可以使用Python语言来实现。下面是一个简单的例子,该游戏会随机生成一定数量的包子,玩家每次可以吃掉一个包子,直到包子被吃光为止。 import random def eat_dumplings():# 随机生成…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...
)
C#学习第29天:表达式树(Expression Trees)
目录 什么是表达式树? 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持: 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...
