前端实现获取后端返回的文件流并下载
前端实现获取后端返回的文件流并下载
- 方法一:使用Axios实现文件流下载
- 优点
- 缺点
- 方法二:使用封装的Request工具实现文件流下载
- 优点
- 缺点
- 方法三:直接通过URL跳转下载
- 优点
- 缺点
- 结论
在前端开发中,有时需要从后端获取文件流,并将其下载到本地。本文介绍如何在前端实现此功能的不同的实现方法,并分析其优缺点
方法一:使用Axios实现文件流下载
使用Axios实现文件流下载的方法,本人亲测可以实现
import axios from 'axios';
import { getToken } from '@/utils/auth'handleExport() {// 接口调用获取文件axios({method: 'get',responseType: 'blob', // 指定响应类型为bloburl: this.GLOBAL.baseURL + '/api/v1/business/user/export',data: this.queryParams, // 导入文件一般都用FormData格式数据headers: { 'Authorization': 'Bearer ' + getToken() } // 传递token进行身份验证}).then(res => {if (res.code === 200) {// 导入成功this.downloadBinaryFile(res.data, '导入失败后下载的报错文件')} else {// 输出失败信息}}).catch(error => {console.error('下载失败', error);});
},/*** 将二进制文件下载到本地,保存为excel文件* @param {*} binFile 二进制文件流* @param {*} fileName 下载后的文件名* @param {*} blobType 文件格式,默认为 "application/vnd.ms-excel"*/
downloadBinaryFile(binFile, fileName, blobType = "application/vnd.ms-excel") {// 创建 Blob 对象,包含二进制文件流和文件类型const blobObj = new Blob([binFile], { type: blobType });// 创建下载链接元素const downloadLink = document.createElement('a');// 处理不同浏览器的 URL 兼容性let url = window.URL || window.webkitURL; url = url.createObjectURL(blobObj); // 创建文件 URL// 设置下载链接属性downloadLink.href = url;downloadLink.download = fileName;// 将下载链接添加到文档中并触发点击事件document.body.appendChild(downloadLink);downloadLink.click();// 移除下载链接并释放 URL 对象document.body.removeChild(downloadLink);window.URL.revokeObjectURL(url);
}
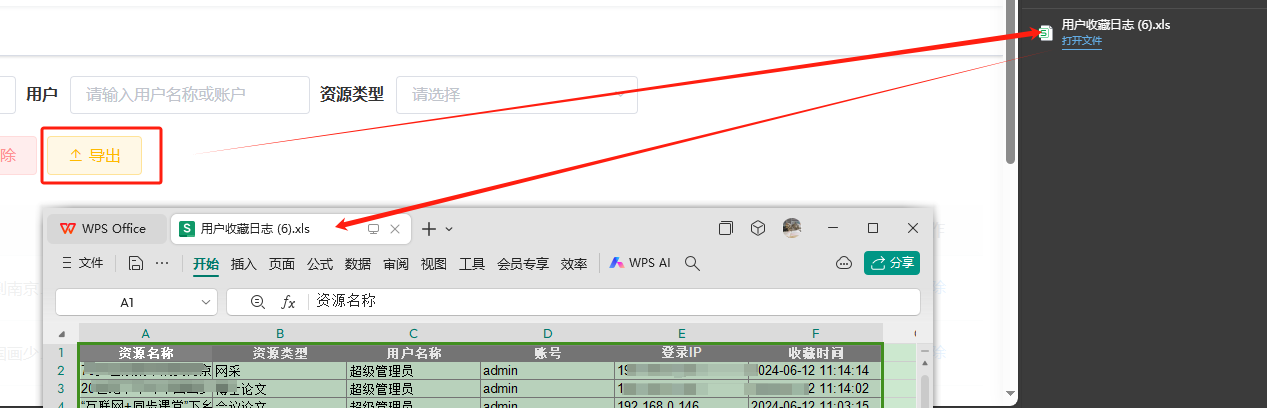
实现的效果
优点
- 支持传递Token进行身份验证,安全性较高
- 支持POST请求,可以将参数放在请求体中,避免URL长度限制及参数暴露
缺点
- 实现相对复杂,需要手动创建和管理Blob对象及下载链接
方法二:使用封装的Request工具实现文件流下载
接下来介绍使用封装的Request工具实现文件流下载的方法
import request from '@/utils/request'// 日志管理收藏、浏览、下载导出接口
export function exportUserOperateAdmin(data, headers) {return request({url: '/business/user/export',method: 'get',data: data,headers: headers})
}// 调用导出接口
exportUserOperateAdmin(this.queryParams, { responseType: 'blob' }).then(response => {console.log(response)const url = window.URL.createObjectURL(new Blob([response.data])) // 创建下载链接const link = document.createElement('a')link.href = urllink.download = '全文导入模板.xlsx' // 设置文件名document.body.appendChild(link)link.click() // 触发下载document.body.removeChild(link) // 下载后移除元素}
).catch(error => {console.error('下载失败', error)this.loading = false // 停止加载,隐藏加载状态
})
优点
- 封装后的Request工具调用简单,代码更简洁
- 支持传递Token进行身份验证,安全性较高
缺点
- 实现相对简单,但仍需手动处理Blob对象及下载链接
方法三:直接通过URL跳转下载
最后介绍直接通过URL跳转实现文件下载的方法
const baseurl = this.GLOBAL.baseURL
// 拼接上导出的地址,如果接口还需要其他参数,都可以直接拼接上
let url = baseurl + '/api/v1/business/user/export';
console.log(url)
alert(url)
// 第二个参数'_self'表示在当前页下载,不打开新的页面
window.open(url, '_self')
优点
- 实现简单,不需要处理Blob对象及下载链接
- 适合下载无需身份验证或参数简单的文件
缺点
- 无法传递Token进行身份验证,安全性较低
- 参数放在URL中不安全,且可能会导致URL过长
- 处理中文参数可能会出现乱码问题
结论
以上三种方法各有优缺点,实际开发中可以根据具体需求选择合适的方法。
如果需要传递Token进行身份验证并确保下载安全性,推荐使用方法一或方法二
如果只是简单下载无需验证的文件,可以考虑使用方法三
相关文章:

前端实现获取后端返回的文件流并下载
前端实现获取后端返回的文件流并下载 方法一:使用Axios实现文件流下载优点缺点 方法二:使用封装的Request工具实现文件流下载优点缺点 方法三:直接通过URL跳转下载优点缺点 结论 在前端开发中,有时需要从后端获取文件流࿰…...
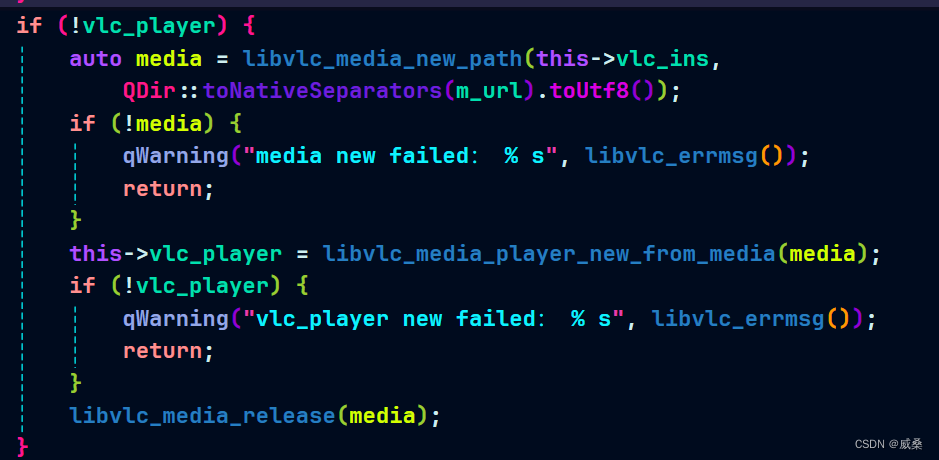
Windows下对于Qt中带 / 的路径的处理
在Windows下,如果你想使用操作系统的分隔符显示用户的路径,请使用 toNativeSeparators()。 请看以下代码: void Player::on_playBtn_clicked() {if (this->m_url.isEmpty()) {openMedia();if (this->m_url.isEmpty())return;}qDebug(…...
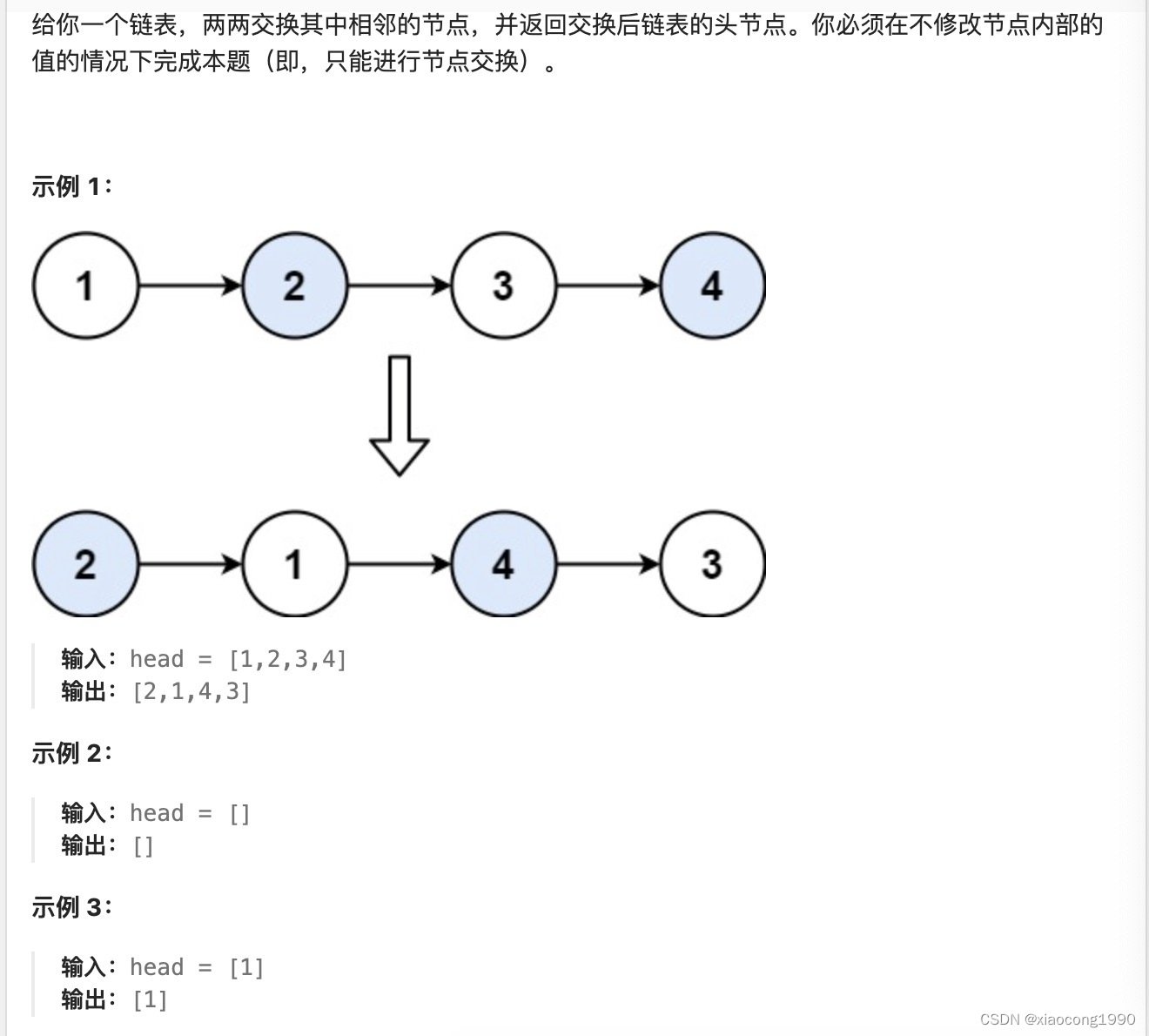
[leetcode]swap-nodes-in-pairs
. - 力扣(LeetCode) class Solution { public:ListNode* swapPairs(ListNode* head) {ListNode* dummyHead new ListNode(0);dummyHead->next head;ListNode* temp dummyHead;while (temp->next ! nullptr && temp->next->next !…...

国思RDIF.vNext全新低代码快速开发框架平台6.1版本发布(支持vue2、vue3)
1、平台介绍 RDIF.vNext,全新低代码快速开发集成框架平台,给用户和开发者最佳的.Net框架平台方案,为企业快速构建跨平台、企业级的应用提供强大支持。 RDIF.vNext的前身是RDIFramework框架,RDIF(Rapid develop Integrate Framewor…...
中国地市分布图
原文链接https://mp.weixin.qq.com/s?__bizMzUyNzczMTI4Mg&mid2247693904&idx1&snb54884975272eaecb1d0564cafc128d3&chksmfa76a96dcd01207b939b8852a08eea9852eeffa8cc51a3af055dfca5c999e93301237e95901b&token1851596113&langzh_CN#rd...

HCIA11 网络安全之本地 AAA 配置实验
AAA 提供 Authentication(认证)、Authorization(授权)和 Accounting(计费)三种安全功能。 • 认证:验证用户是否可以获得网络访问权。 • 授权:授权用户可以使用哪些服务。 •…...
用Python处理Excel的资源
用Python处理Excel的资源 python-excel 读写Excel文件 openpyxl openpyx文档l 读写Excel2010文件(即xlsx) openpyxl示例: from openpyxl import Workbook wb Workbook()# 获取active worksheet ws wb.active# 给单元格赋值 ws[A1] 4…...

2024年中国移动游戏市场研究报告
来源:点点数据: 近期历史回顾: 面向水泥行业的5G虚拟专网技术要求(2024).pdf 2024年F5G-A绿色万兆全光园区白皮书.pdf 2024年全球废物管理展望报告.pdf 内容管理系统 2024-2025中国羊奶粉市场消费趋势洞察报告.pdf 20…...

JS-12-es6常用知识-async
目录 1. 定义与概述 2. 使用方法 3. 注意事项 4. 应用场景 5. 示例代码 6.总结 async 是 JavaScript(包括 TypeScript)中的一个关键字,用于声明一个函数为异步函数。async其实是一个promise的语法糖,以下是关于 async 的详细…...

使用winscp 通过中转机器(跳板机、堡垒机)密钥远程连接服务器,保姆级别教程
1.winscp下载地址 winscp下载 2.安装自己选择位置 3.连接服务器 到这里,基本就是没有壁垒机的就可直接连接,传递文件 4.配置中转服务器(壁垒机、跳板机) 选择高级选项 配置utf-8的编码格式 配置中转服务器(壁垒机、跳板机) 设置中专机的密码或者私钥 配置私钥...

力扣-1984. 学生分数的最小差值
文章目录 力扣题目工程代码C实现python实现 力扣题目 给你一个 下标从 0 开始 的整数数组 nums ,其中 nums[i] 表示第 i 名学生的分数。另给你一个整数 k 。 从数组中选出任意 k 名学生的分数,使这 k 个分数间 最高分 和 最低分 的 差值 达到 最小化 。…...

激动人心的LayerDiffusion终于可以在ComfyUI中使用了
一、什么是LayerDiffusion 随着Stable Diffusion等散射模型的蓬勃发展,人工智能图形生成进入了一个崭新的阶段。我们可以仅仅通过文字提示,就可以让AI模型为我们生成逼真的图像。但是,目前主流的AI生成模型大多只能生成普通的RGB图像,对生成具有透明通道的图片能力还非常有限。…...
 方法的定义与作用)
【JVM】finalize() 方法的定义与作用
finalize() 方法的定义与作用 定义 finalize() 方法是 Java 中的一种特殊方法,定义在 java.lang.Object 类中。它在对象被垃圾回收之前由垃圾回收器调用,用于执行清理操作。 方法签名: protected void finalize() throws Throwable作用 …...

这10个前端库,帮我在工作中赢得了不少摸鱼时间!!
文章目录 前言1、dayjs2、 lodash3、 Quill4、 crypto-js5、 viewerjs6、 localforage7、 vconsole8、 uuid9、 copy-text-to-clipboard10、 classnames前言 通过高效的工具提高工作效率,从而有更多的时间来处理其他重要的任务,或者……摸鱼。没错!就是摸鱼。毕竟,提高效率…...
CentOS 7上在线安装MySQL 5.7)
(2024最新)CentOS 7上在线安装MySQL 5.7
在CentOS 7上安装MySQL 5.7并配置允许远程连接,以下是详细步骤: 1. 添加MySQL官方存储库 首先,下载并添加MySQL的官方存储库。默认情况下,添加的存储库可能会包含最新的MySQL版本(如MySQL 8.0),…...

【C++高阶】C++继承学习手册:全面解析继承的各个方面
📝个人主页🌹:Eternity._ ⏩收录专栏⏪:C “ 登神长阶 ” 🤡往期回顾🤡:模板进阶 🌹🌹期待您的关注 🌹🌹 继承 📖1. 继承的概念及定义…...

使用GPT-soVITS再4060下2小时训练声音模型以及处理断句带来的声音模糊问题
B站UP主视频 感谢UP主“白菜工厂1145号员工”的“熟肉”,我这篇笔记就不展示整一个训练和推理流程,重点写的4060该注意的一些事项。如何解决断句模糊的问题,在本篇笔记的最末尾。 相关连接: 原项目github UP主的说明文档 1、训…...
如何对stm32查看IO功能。
有些同学对于别人的开发板的资源,或者IO口,或者串口等资源不知道怎么分配。 方法1、看硬石、野火、正点原子的开发板,看下他们的例子,那个资源用什么。自己多看几个原理图,多看几个视频,做一下笔记。以后依…...
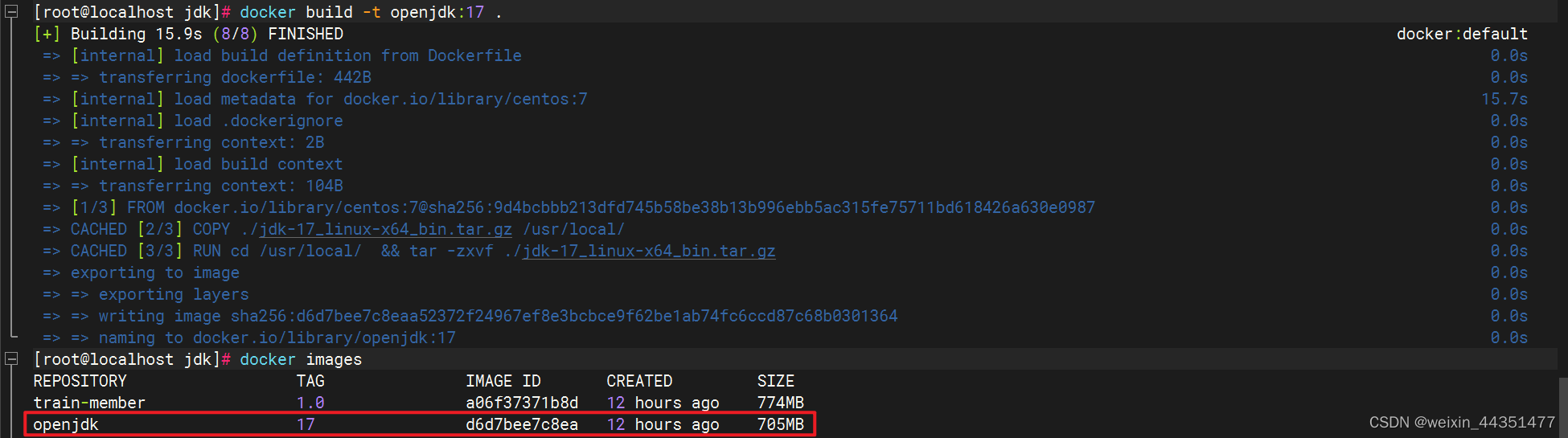
docker构建jdk17镜像
资料参考 参考自黑马教程:10.Docker基础-自定义镜像_哔哩哔哩_bilibili 更多详细语法声明,请参考官网文档:https://docs.docker.com/engine/reference/builder 初步准备 1、下载jdk17包(linux版),我这边版…...
Android Uri转File path路径,Kotlin
Android Uri转File path路径,Kotlin /*** URI转化为file path路径*/private fun getFilePathFromURI(context: Context, contentURI: Uri): String? {val result: String?var cursor: Cursor? nulltry {cursor context.contentResolver.query(contentURI, null…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...
