当前位置： 首页 > news >正文

2024中国网络安全产品用户调查报告（发布版）

news 2026/2/9 1:10:10

       自2020年始，人类进入了21世纪的第二个十年，全球进入了百年未有之大变局，新十年的开始即被新冠疫情逆转了全球化发展的历程，而至2022年3月俄乌战争又突然爆发，紧接着2023年7月“巴以冲突"皱起，世界快速进入动荡中，不确定性激增，网络对抗愈演愈烈，导致中国网络安全市场和环境受到重大影响。
作为国内最具影响力的信息安全专业媒体之一，安在新媒体，从2015年成立以来，一贯秉持专业内涵和大众视角之基调，以人物采访、热点报道、品牌推广、资源对接等方式，为中国网络安全产业发展摇旗助力。而由安在新媒体发起并组织的企业网络安全专家联盟暨“诸子云“社群，更是把视角聚焦在除攻防圈、技术圈、厂商圈之外网络安全产业不可或缺的阵地--网络安全用户企业，也就是我们俗称的"甲方”。

      本报告正是安在新媒体发起，基于“诸子云社群，以“取之于民，用之于民"的方式，反馈“甲方"眼中的中国网络安全市场情况，为网络安全行业提供来自网络安全企业用户视角的参考。本次调查报告是继2020年以来，连续五年的第五期报告，获取来自企业用户的调查样本3783份，经过去重和筛选，获得有效样本3423份，覆盖了全国30个省市及自治区及13个主要行业。

相关文章：

2024中国网络安全产品用户调查报告（发布版）

自2020年始，人类进入了21世纪的第二个十年，全球进入了百年未有之大变局，新十年的开始即被新冠疫情逆转了全球化发展的历程，而至2022年3月俄乌战争又突然爆发，紧接着2023年7月“巴以冲突"皱起，世界快速…...

编程日记 2024/6/13 12:19:24

手写图片懒加载

参考来自前辈 Aidan路修远i 的文章面试官&#xff1a;请你手写一下&#xff01;懒加载 - 掘金 (juejin.cn) Hello.vue <template><div><!-- src里面为空&#xff0c;data-original里面写图片真正的url(此处省略) --><img src"" data-origina…...

编程日记 2024/6/13 12:16:21

大型语言模型（LLMs）的后门攻击和防御技术

大型语言模型&#xff08;LLMs&#xff09;通过训练在大量文本语料库上&#xff0c;展示了在多种自然语言处理&#xff08;NLP&#xff09;应用中取得最先进性能的能力。与基础语言模型相比&#xff0c;LLMs在少样本学习和零样本学习场景中取得了显著的性能提升&#xff0c;这得…...

编程日记 2024/6/13 12:15:20

力扣2594.修车的最少时间

力扣2594.修车的最少时间 二分答案 class Solution {public:long long repairCars(vector<int>& ranks, int cars) {ranges::sort(ranks);auto check [&](long long x) -> bool{long long res 0;for(auto v : ranks){long long k sqrt(x/v);res k;if(r…...

编程日记 2024/6/13 12:12:16

攻防演练之-成功的钓鱼邮件溯源

书接上文&#xff0c;《网络安全攻防演练风云》专栏之攻防演练之-网络安全产品大巡礼二&#xff0c;这里。 演练第一天并没有太大的波澜&#xff0c;白天的时间过得很快。夜色降临&#xff0c;攻防演练中心内的灯光依旧明亮。对于网络安全团队来说&#xff0c;夜晚和白天并没有…...

编程日记 2024/6/13 12:11:15

Gi标签管理

文章目录 前言理解标签创建标签操作标签总结 前言 理解标签 标签&#xff0c;可以理解为对某次commit的一次标识&#xff0c;相当于起起了一个别名。 例如&#xff0c;在项目发布某个版本时候&#xff0c;针对最后一次commit起一个v1.0这样的标签来标识里程碑的意义。 这有什…...

编程日记 2024/6/13 12:09:13

2024福建等保测评公司有哪些？分别叫做什么名字？

2024福建等保测评公司有哪些&#xff1f;分别叫做什么名字&#xff1f; 【回答】&#xff1a;2024年具有资质的福建等保测评公司有6家&#xff0c;其名称以及地址如下&#xff1a; 1、福建省网络与信息安全测评中心&#xff0c;福州市鼓楼区东街8号利达大厦A座8层&#xff1b…...

编程日记 2024/6/13 12:08:11

王先宏老师厉害了，活页笔记版古琴曲谱拆箱图

王先宏老师走心了&#xff0c;活页笔记版古琴曲谱拆箱图&#xff0c;简直是史上最好的古琴学习利器&#xff01;送的防滑垫还带铝合金夹层的&#xff0c;养弦膏都是市面上没有的的。 这些古琴谱上的笔记就是老师课堂上用的&#xff0c;直接拿来就可以跟着弹&#xff0c;不用您…...

编程日记 2024/6/13 12:05:09

TalkingData 是一家专注于提供数据统计和分析解决方案的独立第三方数据智能服务平台

TalkingData 是一家专注于提供数据统计和分析解决方案的独立第三方数据智能服务平台。通过搜索结果&#xff0c;我们可以了解到 TalkingData 的一些关键特性和市场情况&#xff0c;并将其与同类型产品进行比较。 TalkingData 产品特性 数据统计与分析&#xff1a;提供专业的数…...

编程日记 2024/6/13 12:04:08

Springboot的小型超市商品展销系统-计算机毕业设计源码01635

摘 要 科技进步的飞速发展引起人们日常生活的巨大变化&#xff0c;电子信息技术的飞速发展使得电子信息技术的各个领域的应用水平得到普及和应用。信息时代的到来已成为不可阻挡的时尚潮流&#xff0c;人类发展的历史正进入一个新时代。在现实运用中&#xff0c;应用软件的工作…...

编程日记 2024/6/13 12:03:07

UV胶开裂主要因素有哪些？如何避免？

UV胶开裂主要因素有哪些&#xff1f;如何避免&#xff1f; UV胶开裂的原因可能包括多个方面&#xff1a; 固化不足&#xff1a;UV胶的固化需要足够的紫外线照射。如果照射时间不够&#xff0c;或者紫外线光源的强度不足&#xff0c;胶水可能没有完全固化&#xff0c;从而导致开…...

编程日记 2024/6/13 12:02:05

LogicFlow 学习笔记——3. LogicFlow 基础 节点 Node

节点 Node LogicFlow 内置了一些基础节点&#xff0c;开发者在实际应用场景中&#xff0c;可以基于这些基础节点&#xff0c;定义符合自己业务逻辑的节点。 认识基础节点 LogicFlow是基于svg做的流程图编辑框架&#xff0c;所以我们的节点和连线都是svg基本形状&#xff0c;…...

编程日记 2024/6/13 12:01:03

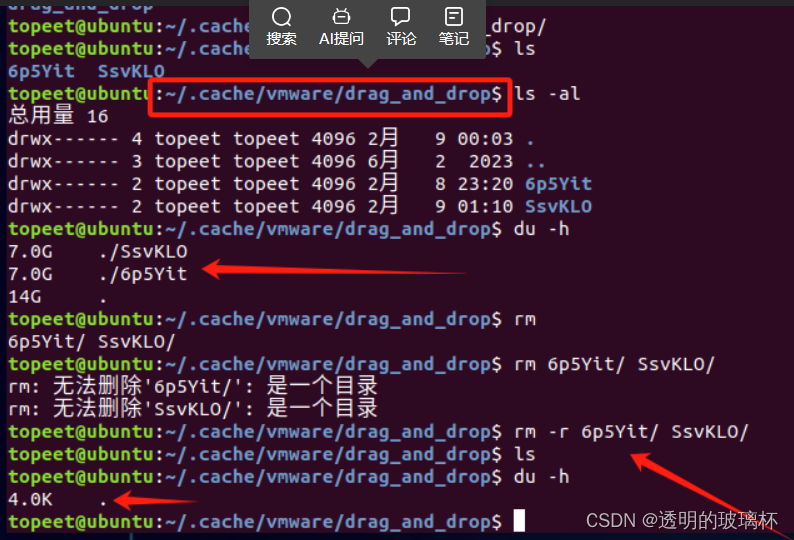
VMware清理拖拽缓存

磁盘空间越用越小&#xff0c;如何快速解决磁盘空间的问题&#xff0c;甩掉烦恼 安装VM tools之后可以通过拖拽的方式把文件拉入虚拟机之中。但每一次拖拽&#xff0c;其实都是现在cache文件夹里面生成一个同样的文件&#xff0c;并使用cp拷贝的方式将其拷贝到拖拽放置的目录中…...

编程日记 2024/6/13 11:58:00

跨语言系统中的功能通信：Rust、Java、Go和C++的最佳实践

在现代软件开发中&#xff0c;使用多种编程语言构建复杂系统已成为一种常见的做法。每种编程语言都有其独特的优势和适用场景&#xff0c;这使得在同一个系统中使用多种语言变得合理且高效。然而&#xff0c;这也带来了一个重要的挑战&#xff1a;如何在这些不同语言之间实现高…...

编程日记 2024/6/13 11:56:58

4. Revit API UI 之 Ribbon（界面）

4. Revit API UI 之 Ribbon&#xff08;界面&#xff09; 第二篇中&#xff0c;我们提到了IExternalApplication&#xff0c;该接口需要实现两个方法&#xff1a;Revit启动时调用的OnStartup 方法&#xff0c;和Revit关闭时调研的OnShutdown 方法。文中还给了个例子&#xff0…...

编程日记 2024/6/13 11:54:57

js数组方法

改变原始数组返回一个新数组添加元素push&#xff0c;unshiftconcat&#xff0c;[…arr] 展开语法删除元素pop&#xff0c;shift&#xff0c;splicefilter&#xff0c;slice替换元素splice&#xff0c;arr[i] … 赋值map排序reverse&#xff0c;sort先将数组复制一份...

编程日记 2024/6/13 11:52:55

PyTorch -- 最常见损失函数 LOSS 的选择

损失函数&#xff1a;度量模型的预测结果与真实值之间的差异&#xff1b;通过最小化 loss -> 最大化模型表现代码实现框架&#xff1a;设有 模型预测值 f (x), 真实值 y 方法一&#xff1a; 步骤 1. criterion torch.nn.某个Loss()&#xff1b;步骤 2. loss criterion(f(x…...

编程日记 2024/6/13 11:50:52

Prometheus 监控系统

一、Prometheus概述 是一个开源的服务监控系统和时序数据库&#xff0c;其提供了通用的数据模型和快捷数据采集、存储和査询接口。它的核心组件. 1.1 Prometheus server 会定期从静态配置的监控目标或者基于服务发现自动配置的目标中进行拉取数据&#xff0c;新拉取到的数据会…...

编程日记 2024/6/13 11:48:50

Spring Boot中使用logback出现LOG_PATH_IS_UNDEFINED文件夹

1.首先查看&#xff0c;application.properties 文件是否按格式编写 logging.pathmylogs logging.configclasspath:logback-spring.xml2.查看 logback-spring.xml <springProperty scope"context" name"LOG_HOME" source"logging.path"/> …...

编程日记 2024/6/13 11:47:49

代码随想录——组合总数Ⅲ（Leetcode216）

题目链接 回溯 class Solution {List<List<Integer>> res new ArrayList<List<Integer>>();List<Integer> list new ArrayList<Integer>();public List<List<Integer>> combinationSum3(int k, int n) {backtracking(k, …...

编程日记 2024/6/13 11:46:47

React第五十七节 Router中RouterProvider使用详解及注意事项

前言 在 React Router v6.4 中&#xff0c;RouterProvider 是一个核心组件&#xff0c;用于提供基于数据路由&#xff08;data routers&#xff09;的新型路由方案。 它替代了传统的 <BrowserRouter>&#xff0c;支持更强大的数据加载和操作功能&#xff08;如 loader 和…...

编程新知 2026/1/21 9:06:43

《用户共鸣指数（E）驱动品牌大模型种草：如何抢占大模型搜索结果情感高地》

在注意力分散、内容高度同质化的时代&#xff0c;情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现&#xff0c;消费者对内容的“有感”程度&#xff0c;正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中&#xff0…...

编程新知 2026/2/2 1:48:09

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力

引言&#xff1a; 在人工智能快速发展的浪潮中&#xff0c;快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型&#xff08;LLM&#xff09;。该模型代表着该领域的重大突破&#xff0c;通过独特方式融合思考与非思考…...

编程新知 2026/2/6 19:29:20

什么是库存周转？如何用进销存系统提高库存周转率？

你可能听说过这样一句话&#xff1a; “利润不是赚出来的&#xff0c;是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业&#xff0c;很多企业看着销售不错&#xff0c;账上却没钱、利润也不见了&#xff0c;一翻库存才发现&#xff1a; 一堆卖不动的旧货…...

编程新知 2026/1/26 13:21:10

【Go】3、Go语言进阶与依赖管理

前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课&#xff0c;做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程&#xff0c;它的核心机制是 Goroutine 协程、Channel 通道&#xff0c;并基于CSP&#xff08;Communicating Sequential Processes&#xff0…...

编程新知 2025/10/7 0:32:40

04-初识css

一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

编程新知 2026/1/29 17:54:05

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变（硬件篇）

本项目是基于 STM32F103C8T6 微控制器的 SPWM（正弦脉宽调制）电源模块，能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路，图中 D1 为二极管， 其目的是防止正负极电源反接， …...

编程新知 2026/1/25 3:29:22

BLEU评分：机器翻译质量评估的黄金标准

BLEU评分&#xff1a;机器翻译质量评估的黄金标准 1. 引言 在自然语言处理(NLP)领域&#xff0c;衡量一个机器翻译模型的性能至关重要。BLEU (Bilingual Evaluation Understudy) 作为一种自动化评估指标&#xff0c;自2002年由IBM的Kishore Papineni等人提出以来&#xff0c;…...

编程新知 2026/1/13 7:39:19

鸿蒙（HarmonyOS5）实现跳一跳小游戏

下面我将介绍如何使用鸿蒙的ArkUI框架&#xff0c;实现一个简单的跳一跳小游戏。 1. 项目结构 src/main/ets/ ├── MainAbility │ ├── pages │ │ ├── Index.ets // 主页面 │ │ └── GamePage.ets // 游戏页面 │ └── model │ …...

编程新知 2025/11/20 18:21:59

在Zenodo下载文件 用到googlecolab googledrive

方法&#xff1a;Figshare/Zenodo上的数据/文件下载不下来&#xff1f;尝试利用Google Colab &#xff1a;https://zhuanlan.zhihu.com/p/1898503078782674027 参考&#xff1a; 通过Colab&谷歌云下载Figshare数据&#xff0c;超级实用&#xff01;&#xff01;&#xff0…...

编程新知 2026/2/4 16:07:16