PyTorch -- 最常见损失函数 LOSS 的选择
- 损失函数:度量模型的预测结果与真实值之间的差异;通过
最小化 loss-> 最大化模型表现 - 代码实现框架:设有 模型预测值
f (x), 真实值y- 方法一: 步骤 1.
criterion = torch.nn.某个Loss();步骤 2.loss = criterion(f(x), y) - 方法二:直接采用
F.某个_loss(f(x), y)
- 方法一: 步骤 1.
回归损失(Regression Loss)
- 【
torch.nn.L1Loss()】平均绝对值误差MAE(Mean Abs Error): f (x) 和 y 之间差的绝对值的平均值- 具体数学计算公式: Loss = 1 n ∑ i = 0 n ∣ f ( x i ) − y ∣ \text{Loss}=\frac{1}{n}\sum^n_{i=0} |f(x_i)-y| Loss=n1∑i=0n∣f(xi)−y∣
- 注:L1 损失, 主要用于回归问题和简单的模型,所以很少使用
- 【
torch.nn.MSELoss()】平均平方误差MSE(Mean Squared Error): f (x) 和 y 之间差的平方的平均值- 具体数学计算公式: Loss = 1 n ∑ i = 0 n ( f ( x i ) − y ) 2 \text{Loss}=\frac{1}{n}\sum^n_{i=0} (f(x_i)-y)^2 Loss=n1∑i=0n(f(xi)−y)2:
F.mse_loss(f(x), y) - 注:L2 损失, 很常用
- 具体数学计算公式: Loss = 1 n ∑ i = 0 n ( f ( x i ) − y ) 2 \text{Loss}=\frac{1}{n}\sum^n_{i=0} (f(x_i)-y)^2 Loss=n1∑i=0n(f(xi)−y)2:
分类损失(Classification Loss)logistic regression
- 【
torch.nn.CrossEntropyLoss()】多分类交叉熵损失函数 Cross Entropy Loss:- 具体数学计算公式: Loss = ∑ y i log ( f ( x i ) ) \text{Loss}=\sum y_i \log(f(x_i)) Loss=∑yilog(f(xi)), 注意其中 f ( x i ) f(x_i) f(xi) 表示模型预测出的概率值如 [0.1, 0.7, 0.2]
- 通常和
softmax(soft version of max S ( y i ) = e y i ∑ e y i S(y_i) = \frac{e^{y_i}}{\sum e^{y_i}} S(yi)=∑eyieyi:F.softmax(y)) 搭配使用 (softmax 负责产生上述概率输出)
- B站视频参考资料
- 详细博客参考资料
相关文章:

PyTorch -- 最常见损失函数 LOSS 的选择
损失函数:度量模型的预测结果与真实值之间的差异;通过最小化 loss -> 最大化模型表现代码实现框架:设有 模型预测值 f (x), 真实值 y 方法一: 步骤 1. criterion torch.nn.某个Loss();步骤 2. loss criterion(f(x…...

Prometheus 监控系统
一、Prometheus概述 是一个开源的服务监控系统和时序数据库,其提供了通用的数据模型和快捷数据采集、存储和査询接口。它的核心组件. 1.1 Prometheus server 会定期从静态配置的监控目标或者基于服务发现自动配置的目标中进行拉取数据,新拉取到的数据会…...

Spring Boot中使用logback出现LOG_PATH_IS_UNDEFINED文件夹
1.首先查看,application.properties 文件是否按格式编写 logging.pathmylogs logging.configclasspath:logback-spring.xml2.查看 logback-spring.xml <springProperty scope"context" name"LOG_HOME" source"logging.path"/> …...

代码随想录——组合总数Ⅲ(Leetcode216)
题目链接 回溯 class Solution {List<List<Integer>> res new ArrayList<List<Integer>>();List<Integer> list new ArrayList<Integer>();public List<List<Integer>> combinationSum3(int k, int n) {backtracking(k, …...

Android native层的线程分析(C++),以及堆栈打印调试
文章目录 Android native层的线程分析(C),多线程实现1.native线程的创建第一部分:android_thread模块第二部分:linux_thread模块 2.测试linux_thread模块3.Android native的Thread类3.1源码分析 4.native层堆栈调试方法 Android native层的线…...

计算机科学:2024年高考生的明智之选?兴趣与趋势并重的决策指南
站在2024年这个时间节点上,计算机相关专业依然保持着其“万金油”地位,尽管面临一定的挑战,但其长期发展前景和就业潜力仍然乐观。以下是从不同身份角度出发的观点分析: 高考生视角: 如果你是今年的高考生࿰…...
跨界合作机会:通过淘宝数据挖掘潜在的合作伙伴与市场拓展方向
淘宝平台汇聚了众多商家和消费者,生成了大量的交易数据,这些数据为商家提供了挖掘跨界合作机会和市场拓展方向的丰富线索。以下是如何利用淘宝数据来寻找潜在的合作伙伴和探索新的市场机会的一些策略: 消费者行为分析:通过跟踪消费…...

如何利用智能家居打造一个“会呼吸的家”?一体化电动窗帘
如何利用智能家居打造一个“会呼吸的家”?一体化电动窗帘 史新华 隐藏式一体化智能电动窗帘与市面上其他窗帘不同的是,电机内置于轨道之中,一体化,美观、安静、滑动顺畅。 每次都会自动打开和关闭,相当漂亮。 众多家庭…...
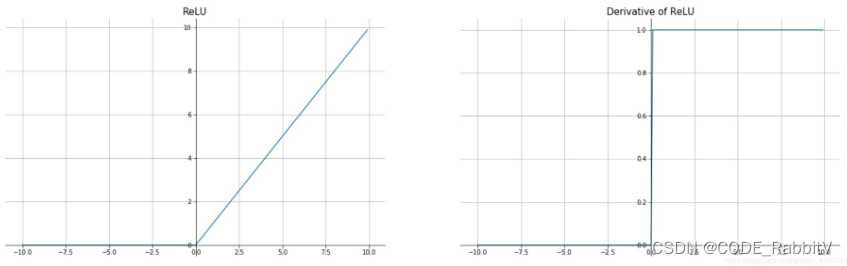
PyTorch -- 最常见激活函数的选择
首先,简单复习下什么是梯度:梯度是偏微分的集合 举例说明:对于 z y 2 − x 2 : ∇ z ( ∂ z ∂ x , ∂ z ∂ y ) ( 2 x , 2 y ) z y^2-x^2: \nabla z (\frac{\partial z}{\partial x}, \frac{\partial z}{\partia…...

人工智能--制造业和农业
欢迎来到 Papicatch的博客 文章目录 🍉人工智能在制造业中的应用 🍈 应用场景及便利 🍍生产线自动化 🍍质量控制 🍍预测性维护 🍍供应链优化 🍈 技术实现及核心 🍍机器学习和…...

go语言,拼接字符串有哪些方式
目录 第一种方式: 使用加号"" 第二种方式: 使用fmt.Sprintf 第三种方式: 使用strings.Join 第四种方式: 使用strings.Builder 第五种方式: 使用bytes.Buffer go语言,拼接字符串的方式有…...

C++类型转换深度解析:从基础数据类型到字符串,再到基础数据类型的完美转换指南
前言 在 C 编程中,我们经常需要在基础数据类型(如 int、double、float、long、unsigned int 等)与 string 类型之间进行转换。这种转换对于处理用户输入、格式化输出、数据存储等场景至关重要。 本文将详细介绍如何在 C 中实现这些转换。 文…...
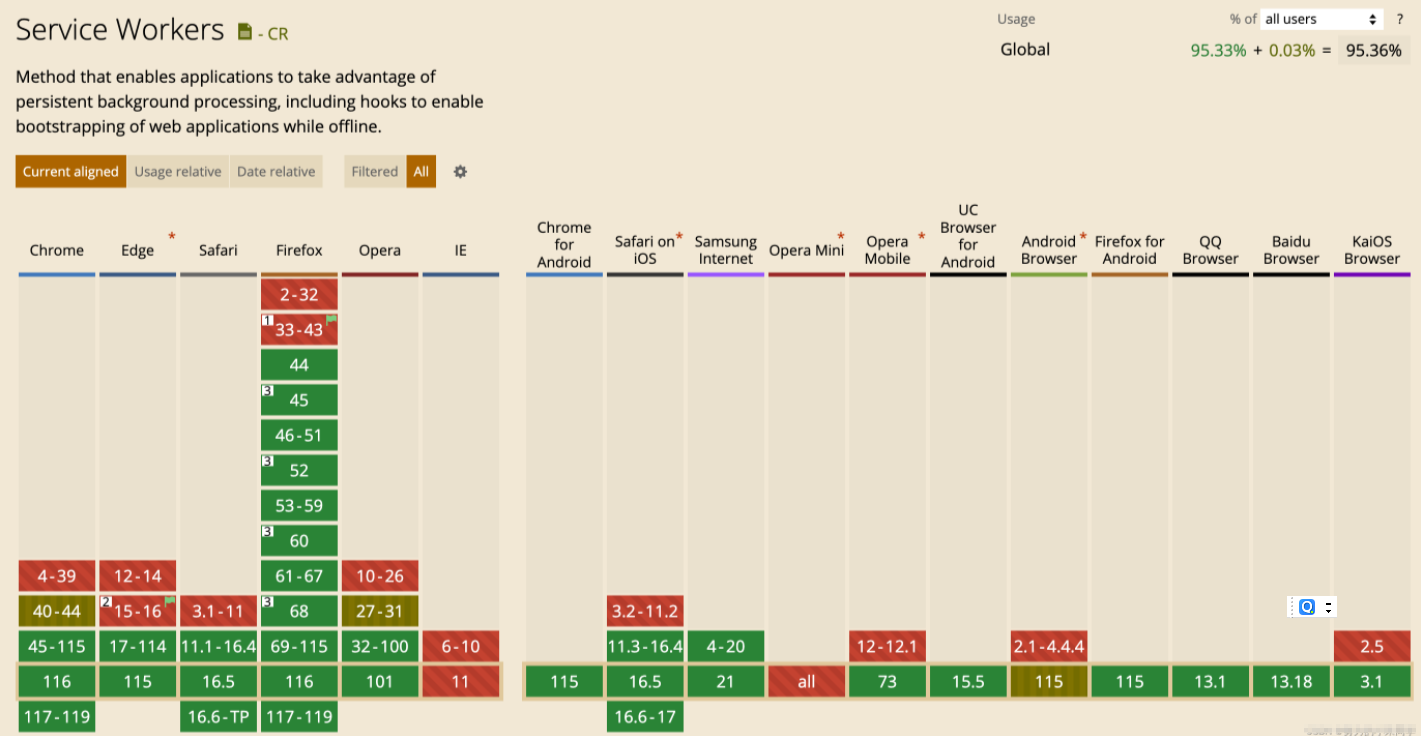
一文了解:渐进式web应用(PWA),原生应用还香吗?
前端开发是一个充满活力和不断演进的领域,各类技术层出不穷,PWA模式的出现就是想让web移动应用获得原生一样的体验,同时有大幅度降低开发成本,那么它到底能行吗?贝格前端工场带领大家了解一下。 一、什么是渐进式web应…...
SOLIDWORKS学生支持 可访问各种产品资源
你是不是一个热爱设计、追求创新的学生?你是不是在寻找一款能够帮助你实现设计梦想的工具?那么,SolidWorks学生支持是你的首要选择! SOLIDWORKS作为三维CAD设计软件,一直致力于为广大学生提供全方面的支持。无论你是初…...
VCS基本仿真
这里记录三种仿真方式: 第一种是将verilog文件一个一个敲在终端上进行仿真; 第二种是将多个verilog文件的文件路径整理在一个文件中,然后进行仿真; 第三种是利用makefile文件进行仿真; 以8位加法器为例: …...

Hbase中Rowkey的设计方法
Hbase中Rowkey的设计方法 过去对于Rowkey设计方法缺乏理解,最近结合多篇博主的文章,进行了学习。有不少心得体会。总结下来供后续学习和回顾。 一、设计Rowkey的三个原则 1.长度原则:长度不能太长,小于100个字节。可以偏端一些…...

Python基础总结之functools.wraps介绍与应用
Python基础总结之functools.wraps介绍与应用 在Python编程中,装饰器(decorator)是一种非常强大的工具,它允许开发者在不改变函数本身的情况下,动态地增加函数的功能。使用装饰器时,常常会用到 functools.wr…...
UE5基础1-下载安装
目录 一.下载 二.安装 三.安装引擎 四.其他 简介: UE5(Unreal Engine 5)是一款功能极其强大的游戏引擎。 它具有以下显著特点: 先进的图形技术:能够呈现出令人惊叹的逼真视觉效果,包括高逼真的光影、材…...
前端实现获取后端返回的文件流并下载
前端实现获取后端返回的文件流并下载 方法一:使用Axios实现文件流下载优点缺点 方法二:使用封装的Request工具实现文件流下载优点缺点 方法三:直接通过URL跳转下载优点缺点 结论 在前端开发中,有时需要从后端获取文件流࿰…...
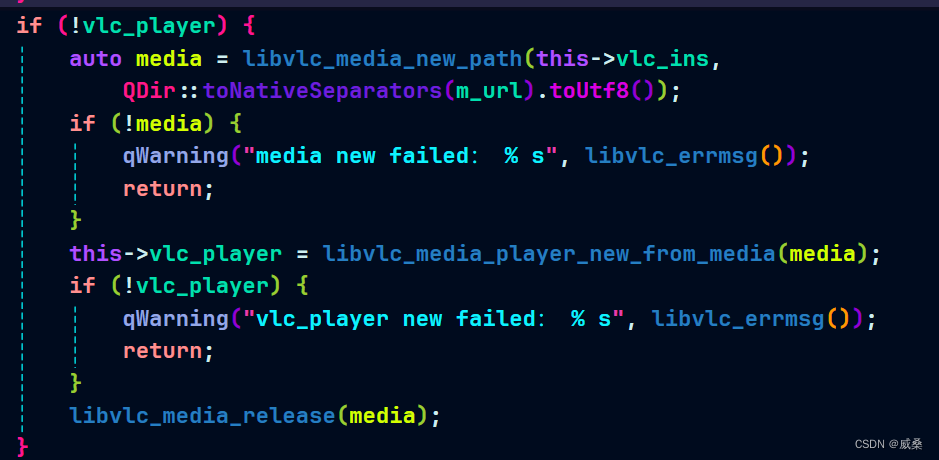
Windows下对于Qt中带 / 的路径的处理
在Windows下,如果你想使用操作系统的分隔符显示用户的路径,请使用 toNativeSeparators()。 请看以下代码: void Player::on_playBtn_clicked() {if (this->m_url.isEmpty()) {openMedia();if (this->m_url.isEmpty())return;}qDebug(…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...
