【数据结构与算法(C语言)】循环队列图解
目录
- 1. 前言
- 1.1 普通循环队列假溢出
- 1.1.1 初始化队列
- 1.1.2 插满队列
- 1.1.3 删除元素后,再插入元素
- 1.2 循环队列
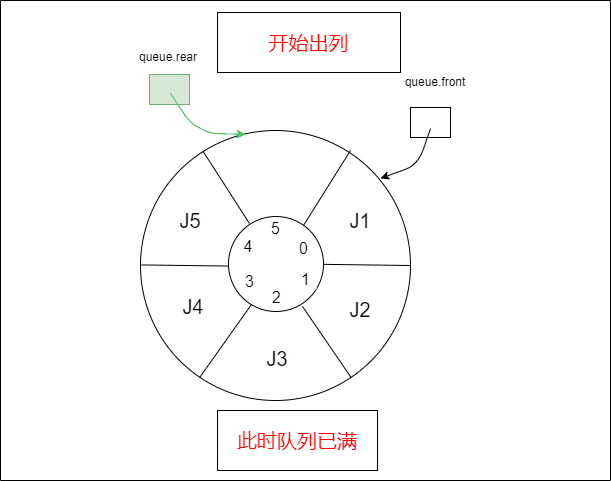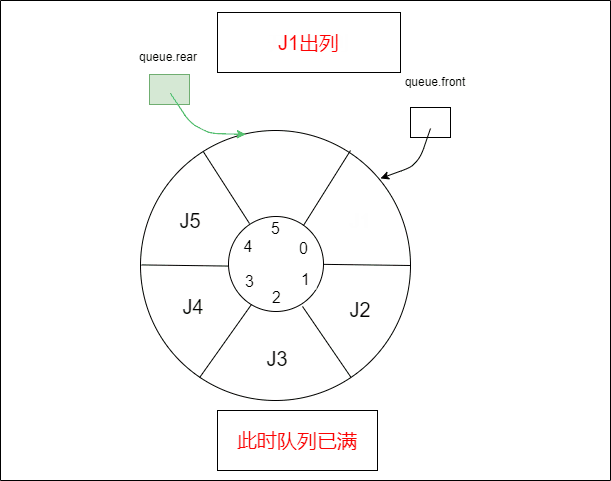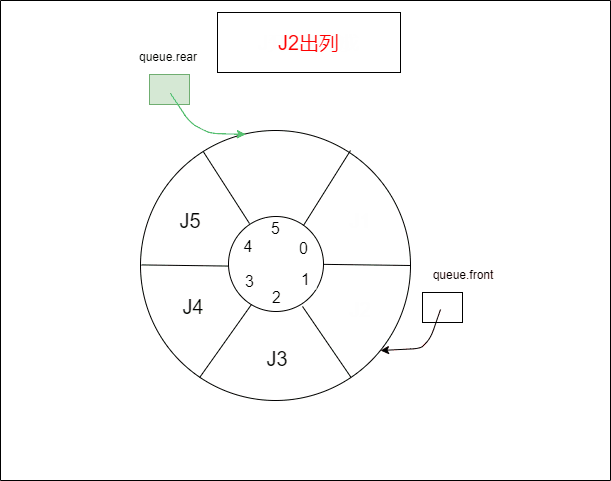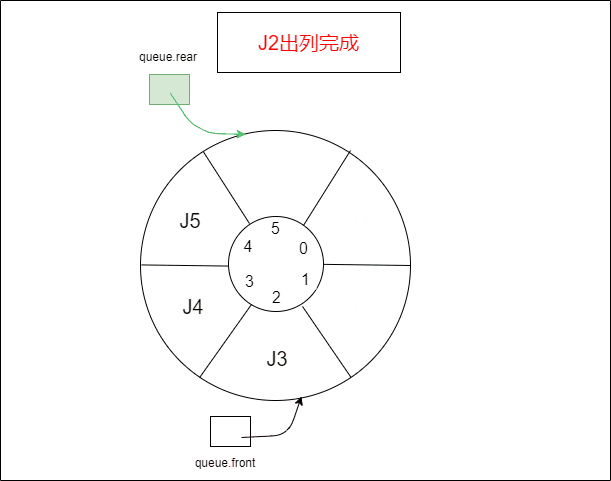
- 1.2.1 插入元素,队列已满
- 1.2.2 将元素J1、J2出列,循环队列又空出两个空间
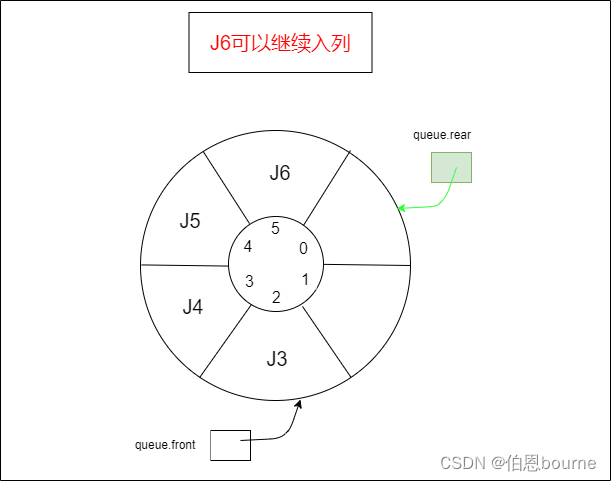
- 1.2.3 元素J6可以继续入列
- 2. 存储结构和函数说明
- 2.1 队列的结构
- 2.2 基本操作函数
- 2.3 初始化队列
- 2.4 销毁队列 DestroyQueue
- 2.5 清空队列 ClearQueue
- 2.6 获取队列第一个元素 GetHead
- 2.7 获取队列长度
- 2.8 元素入列 EnQueue
- 2.9 元素出列 DeQueue
- 2.10 遍历队列 QueueTraverse
- 3. 完整源码和测试代码
- 4. 测试结果
- 5. 小结
- 5.1 优点:
- 5.2 缺点
1. 前言
将队列的头尾相接,臆造成环状的顺序存储结构称为循环队列。
普通的顺序存储队列会出现 假溢出 情况。如下面三张图(三个步骤)描述的情况
1.1 普通循环队列假溢出
下面来看看普通队列是如何产生假溢出现象的。
1.1.1 初始化队列
此时队列为空队列。头指针和尾指针都指向第一个空间
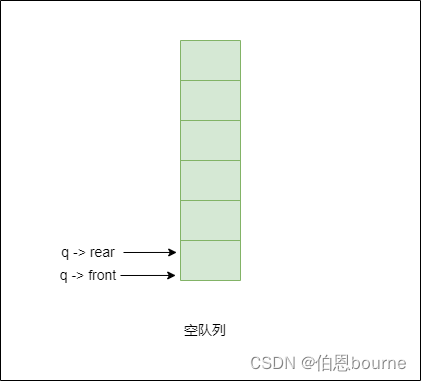
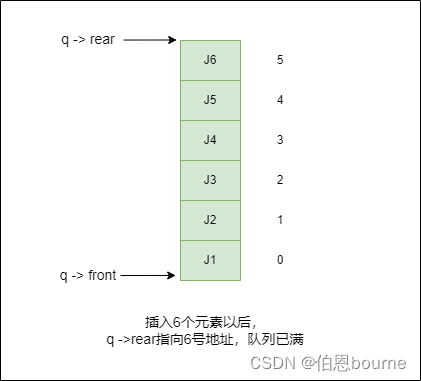
1.1.2 插满队列
插入J1、J2、J3、J4、J5、J6,因为q->rear=6,说明队列已满
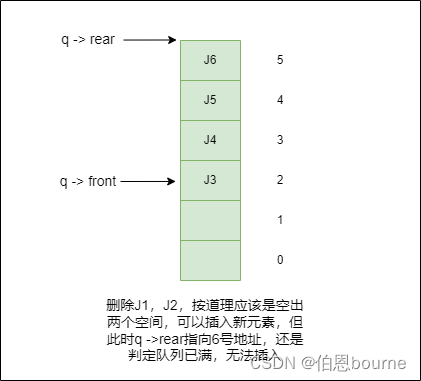
1.1.3 删除元素后,再插入元素
删除J1,J2,按道理应该是空出两个空间,可以插入新元素,但此时q ->rear指向6号地址,还是判定队列已满,如果再插入元素,q-rear=7,则队列溢出。但实际队列是有空间的
1.2 循环队列
普通的循环队列有上述假溢出缺点。于是乎,循环队列就应运而生了。
循环队列的解决假溢出方法 如下面三张图中展示的步骤:
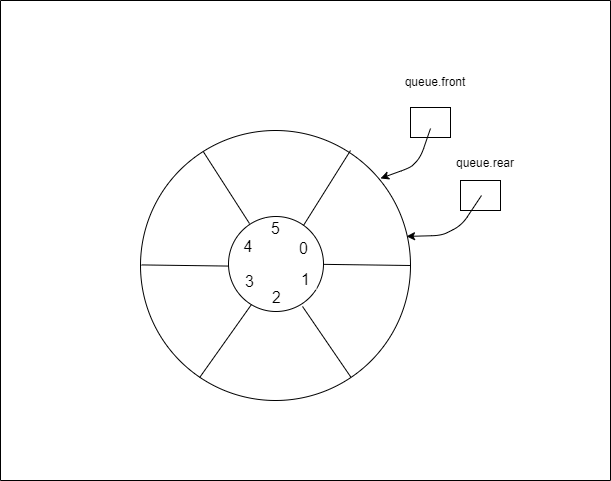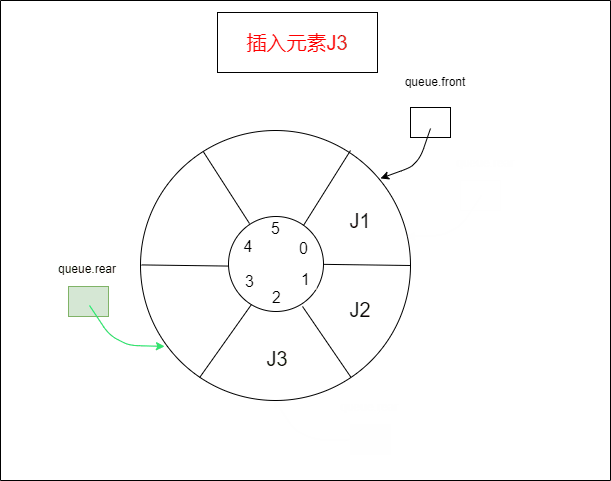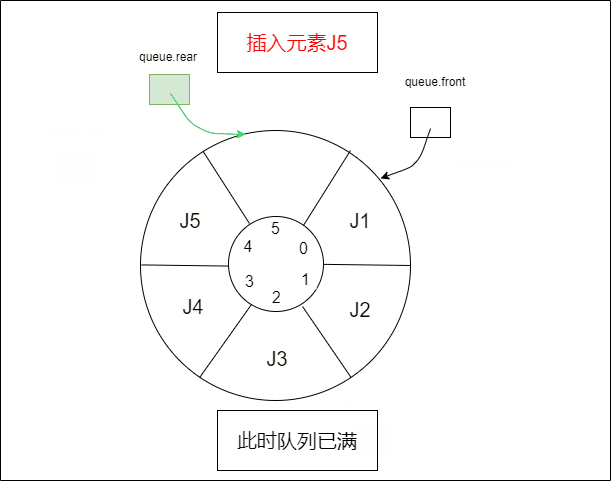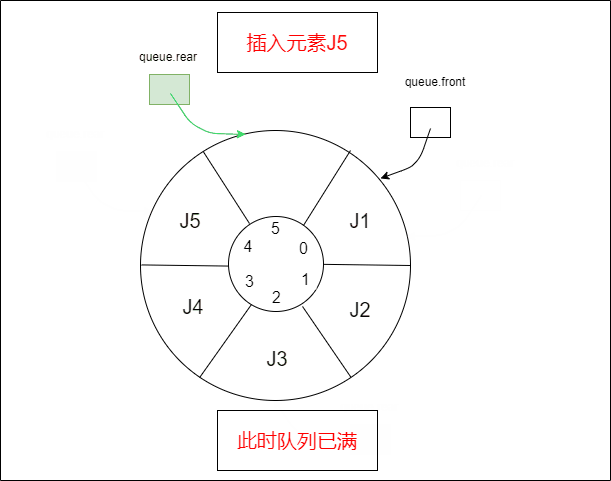
1.2.1 插入元素,队列已满
还剩一个空间的时候,队列就满了。这样设置的原因是,如果不浪费一个空间的话,当 queue.front=queue.rear,可能会有两种情况,一个是队列为空,一个是队列已满。如果预留一个空间的话,可以用 queue.rear + 1=queue.front 判断队列已满,这样和队列为空的判断方式不冲突。
1.2.2 将元素J1、J2出列,循环队列又空出两个空间
1.2.3 元素J6可以继续入列
2. 存储结构和函数说明
2.1 队列的结构
typedef struct{QElemType * base; //存储空间 int front; //队列头的下标int rear; //队列尾的下标
}SqQueue; //定义一个队列类型
2.2 基本操作函数
和上一篇博客中的链式队列差不多,一共8个函数。
Status InitQueue(SqQueue * queue); //初始化队列
void DestroyQueue(SqQueue *queue); //销毁队列
Status ClearQueue(SqQueue * queue);//清空队列
Status QueueEmpty(SqQueue queue); //判断队列是否为空
Status GetHead(SqQueue queue ,QElemType * e); //获取队列头元素
int QueueLength(SqQueue queue); //获取队列长度
Status EnQueue(SqQueue * queue, QElemType e); //元素入列
Status DeQueue(SqQueue * queue ,QElemType * e); //元素出列
2.3 初始化队列
原型:Status InitQueue(SqQueue * queue)
说明:初始化队列,申请一个头结点的内存
/*初始化队列,申请一个头结点的内存*/
Status InitQueue(SqQueue * queue)
{queue->base = (QElemType *) malloc(sizeof(QElemType)*MAXSIZE); //申请一个队列结点作为头结点的内存地址给 队头指针;if(queue->base == NULL)return FALSE;queue->front = queue->rear =0;return TRUE;
}2.4 销毁队列 DestroyQueue
原型 :void DestroyQueue(SqQueue *queue)
功能 :销毁队列,释放队列的数据空间
/*销毁栈,释放队列的数据空间*/
void DestroyQueue(SqQueue *queue)
{free(queue->base);queue->front= queue->rear =0;
}
2.5 清空队列 ClearQueue
原型:Status ClearQueue(SqQueue * queue)
功能 :清空队列的元素,但队列的空间保留
//将队列queue清空
Status ClearQueue(SqQueue * queue)
{queue->front = queue->rear = 0;return OK;
}
2.6 获取队列第一个元素 GetHead
原型:Status GetHead(SqQueue queue ,QElemType * e)
功能 :获取队列第一个元素,注意 不是删除元素
//获取队列第一个元素
Status GetHead(SqQueue queue ,QElemType * e)
{if(QueueEmpty(queue))return FALSE;*e=queue.base[queue.front];return TRUE;
}
2.7 获取队列长度
原型:int QueueLength(SqQueue queue)
功能 :队列长度
//返回队列长度
int QueueLength(SqQueue queue)
{return (queue.rear - queue.front + MAXSIZE) % MAXSIZE;
}
2.8 元素入列 EnQueue
原型:Status EnQueue(SqQueue * queue, QElemType e)
功能 :元素e 插入队列queue
//元素e 插入队列queue
Status EnQueue(SqQueue * queue, QElemType e)
{if((queue->rear + 1) % MAXSIZE == queue->front) //队列满,return FALSE ;queue->base[queue->rear]=e; //e 插入队列尾部,队尾加1queue->rear = (queue->rear + 1) % MAXSIZE;return TRUE;
}
2.9 元素出列 DeQueue
原型:Status DeQueue(SqQueue * queue ,QElemType * e)
功能 :若队列queue不空,则删除Q的队头元素,用e返回其值,并返回 OK;否则返回ERROR
//若队列queue不空,则删除Q的队头元素,用e返回其值,并返回 OK;否则返回ERROR
Status DeQueue(SqQueue * queue ,QElemType * e)
{if(QueueEmpty( *queue))return FALSE;*e = queue->base[queue->front];queue->front= (queue->front + 1) % MAXSIZE;return TRUE;
}
2.10 遍历队列 QueueTraverse
原型:Status QueueTraverse(SqQueue queue,void (*visit)())
功能 :遍历队列,对队列的每个元素调用Visit函数
//遍历队列,对队列的每个元素调用Visit函数
Status QueueTraverse(SqQueue queue,void (*visit)())
{int i = queue.front;if(QueueEmpty(queue))return FALSE ;if(queue.front < queue.rear) while(i < queue.rear)visit(queue.base[i++]);else{while(i< MAXSIZE)visit(queue.base[i++]);i=0;while(i<queue.rear)visit(queue.base[i++]);}return TRUE;
}
3. 完整源码和测试代码
#include <stdio.h>
#include <stdlib.h>#define TRUE 1
#define FALSE 0
#define OK 1
#define ERROR 0
#define MAXSIZE 6 //最大值设置为6typedef int Status;typedef int QElemType; //定义元素类型为整型typedef struct{QElemType * base; //存储空间 int front; //队列头的下标int rear; //队列尾的下标
}SqQueue; //定义一个队列类型 Status InitQueue(SqQueue * queue);
void DestroyQueue(SqQueue *queue);
Status ClearQueue(SqQueue * queue);
Status QueueEmpty(SqQueue queue);
Status GetHead(SqQueue queue ,QElemType * e);
int QueueLength(SqQueue queue);
Status EnQueue(SqQueue * queue, QElemType e);
Status DeQueue(SqQueue * queue ,QElemType * e);/*初始化队列,申请一个头结点的内存*/
Status InitQueue(SqQueue * queue)
{queue->base = (QElemType *) malloc(sizeof(QElemType)*MAXSIZE); //申请一个队列结点作为头结点的内存地址给 队头指针;if(queue->base == NULL)return FALSE;queue->front = queue->rear =0;return TRUE;
}/*销毁队列,释放队列的数据空间*/
void DestroyQueue(SqQueue *queue)
{free(queue->base);queue->front= queue->rear =0;
}//将队列queue清空
Status ClearQueue(SqQueue * queue)
{queue->front = queue->rear = 0;return OK;
}//判断队列是否为空
Status QueueEmpty(SqQueue queue)
{return queue.front == queue.rear? TRUE:FALSE;
}//获取队列第一个元素
Status GetHead(SqQueue queue ,QElemType * e)
{if(QueueEmpty(queue))return FALSE;*e=queue.base[queue.front];return TRUE;
}//返回队列长度
int QueueLength(SqQueue queue)
{return (queue.rear - queue.front + MAXSIZE) % MAXSIZE;
}//元素e 插入队列queue
Status EnQueue(SqQueue * queue, QElemType e)
{if((queue->rear + 1) % MAXSIZE == queue->front) //队列满,return FALSE ;queue->base[queue->rear]=e; //e 插入队列尾部,队尾加1queue->rear = (queue->rear + 1) % MAXSIZE;return TRUE;
}//若队列queue不空,则删除Q的队头元素,用e返回其值,并返回 OK;否则返回ERROR
Status DeQueue(SqQueue * queue ,QElemType * e)
{if(QueueEmpty( *queue))return FALSE;*e = queue->base[queue->front];queue->front= (queue->front + 1) % MAXSIZE;return TRUE;}
void Visit(QElemType e)
{printf("%3d",e);
}
//遍历队列,对队列的每个元素调用Visit函数
Status QueueTraverse(SqQueue queue,void (*visit)())
{int i = queue.front;if(QueueEmpty(queue))return FALSE ;if(queue.front < queue.rear) while(i < queue.rear)visit(queue.base[i++]);else{while(i< MAXSIZE)visit(queue.base[i++]);i=0;while(i<queue.rear)visit(queue.base[i++]);}return TRUE;
}int main()
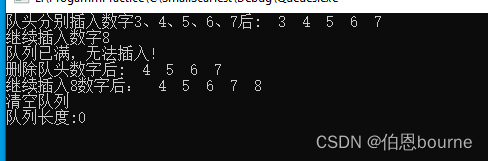
{QElemType e;SqQueue queue;InitQueue(&queue);printf("队头分别插入数字3、4、5、6、7后:");//此时队列已经满了,设置maxsize=6,实际只能存储5个,//因为只剩一个空间,代表队列已满。即 front= (rear+1)%maxsize//如果不留一个空间空着,那么队列满和队列空都是 front=rear,很难分辨EnQueue(&queue,3);EnQueue(&queue,4);EnQueue(&queue,5);EnQueue(&queue,6);EnQueue(&queue,7);QueueTraverse(queue,Visit);printf("\n继续插入数字8");if(EnQueue(&queue,8))printf("\n出问题了,队列满了,还能插入!");elseprintf("\n队列已满,无法插入!");printf("\n删除队头数字后:");DeQueue(&queue,&e); //删除后的队列中还剩4个元素QueueTraverse(queue,Visit);printf("\n继续插入8数字后:");EnQueue(&queue,8); //数字8被存放到queue.base[5]中了QueueTraverse(queue,Visit);printf("\n清空队列");ClearQueue(&queue);printf("\n队列长度:%d\n",QueueLength(queue));DestroyQueue(&queue);getchar();return 0;
}
4. 测试结果
5. 小结
循环队列的优缺点
5.1 优点:
(a) 解决了普通的顺序存储队列的假溢出问题。
(b) 读取方便、快捷
5.2 缺点
存储空间大小固定,无法根据需要进行扩展。
相关文章:

【数据结构与算法(C语言)】循环队列图解
目录 1. 前言1.1 普通循环队列假溢出1.1.1 初始化队列1.1.2 插满队列1.1.3 删除元素后,再插入元素 1.2 循环队列1.2.1 插入元素,队列已满1.2.2 将元素J1、J2出列,循环队列又空出两个空间1.2.3 元素J6可以继续入列 2. 存储结构和函数说明2.1 队…...

私域流量转化不济的原因
你是不是也曾感到私域流量的转化一直不如意?让我来告诉你,这六大问题是为什么,以及如何轻松解决它们,提升你的私域流量转化率! 1. 问题:目标不明确 你是否常常感到茫然,不知道私域流量应该有何目…...

百万上下文RAG,Agent还能这么玩
❝ 在AI技术飞速发展的今天,我们见证了许多令人惊叹的突破。最近,Qwen2模型的开源引起了广泛的关注,它不仅展示了超越闭源模型的能力,还带来了一个全新的框架——Qwen-Agent。 Qwen-Agent的设计思路虽然与LangChain相似࿰…...
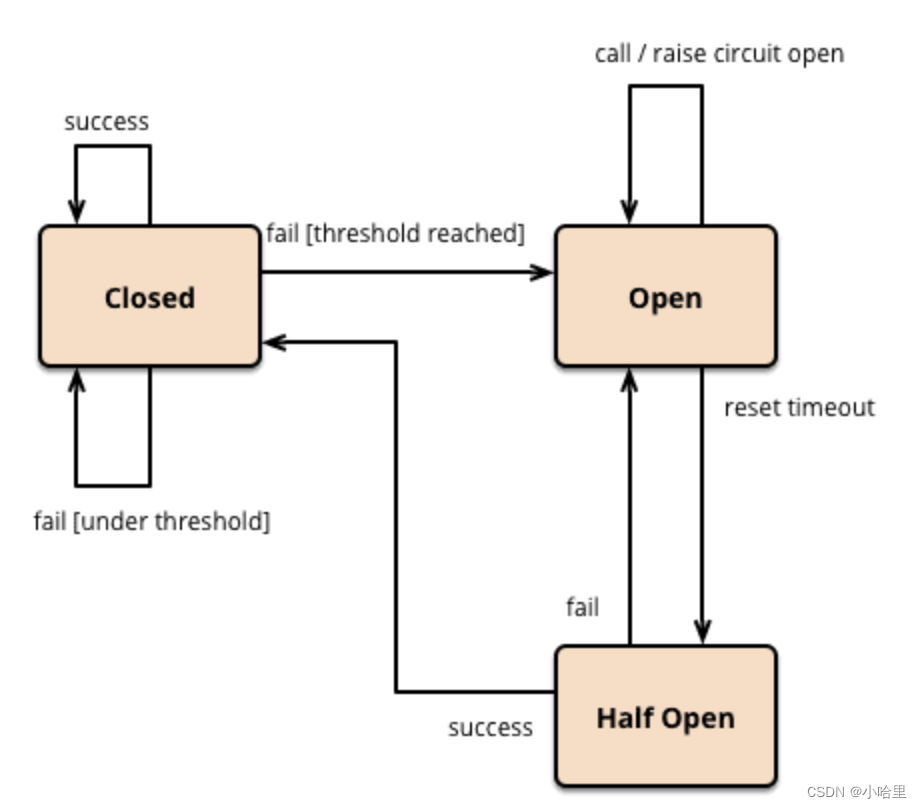
【后端开发】服务开发场景之高可用(冗余设计,服务限流,降级熔断,超时重试,性能测试)
【后端开发】服务开发场景之高可用(冗余设计,服务限流,降级熔断,超时重试,性能测试) 文章目录 序:如何设计一个高可用的系统?可用性的判断指标是什么?哪些情况会导致系统…...
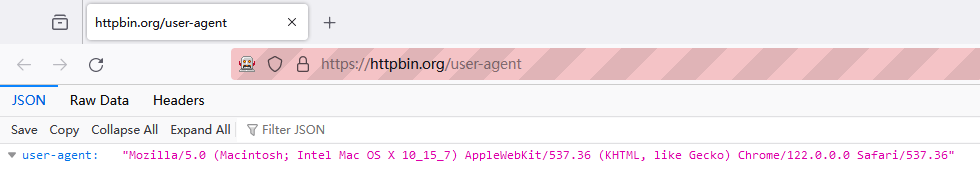
在 Selenium 中更改 User-Agent | 步骤与最佳实践
在 Selenium 中更改 User Agent 是许多网页抓取任务中的关键步骤。它有助于将自动化脚本伪装成常规浏览器,从而避免被网站检测到。本指南将带您了解如何在 Selenium 中更改 Google Chrome 的 User Agent,并提供最佳实践以确保您的网页抓取任务顺利进行。…...
2024酒店IPTV云桌面系统建设方案
Hello大家好,我是点量小芹,这一年多的时间一直在分享实时云渲染像素流相关的内容,今天和大家聊聊酒店IPTV云桌面电视系统解决方案,或者有的朋友也会称之为IPTV服务器。熟悉小芹的朋友知道,IPTV软件系统是我们一直在推的…...

java Thrift TThreadPoolServer 多个processor 的实现
当我们使用Thrift 通信的时候,服务端有时候需要注册多个类,去实现通信,这时候我们就不能再使用单一Processor的方式,就要使用多个Processor,那么如何去实现呢? 多个Process 服务端 public static void m…...

失眠焦虑的解脱之道:找回内心的平静
🍃 在这个快节奏的时代,失眠与焦虑似乎成了许多人的隐形敌人。每当夜幕降临,它们便悄悄潜入心底,扰乱我们的思绪,让宁静的夜晚变得无比漫长。然而,生活总有办法让我们找回内心的平静,只需稍作调…...

OLED柔性屏的显示效果如何
OLED柔性屏的显示效果非常出色,具有多方面的优势。以下是关于OLED柔性屏显示效果的详细分析: 色彩表现:OLED柔性屏的每个像素都可以独立发光,因此色彩准确性极高。黑色呈现得非常深邃,而亮部则展现出鲜明而生动的细节。…...

百货商城优选 伊利牛奶推出全国首款减甲烷环保学生奶
近日,伊利集团受邀参加在全国首个“国际首脑峰会零碳场馆”召开的“降碳增产科技助力奶业绿色高质量发展”首款低碳饲料创新大会。会上,伊利宣布将推出全国首款减甲烷环保学生牛奶——伊利QQ星学生纯牛奶,进一步将可持续发展落到实处…...

Fluid 1.0 版发布,打通云原生高效数据使用的“最后一公里”
作者:顾荣 前言 得益于云原生技术在资源成本集约、部署运维便捷、算力弹性灵活方面的优势,越来越多企业和开发者将数据密集型应用,特别是 AI 和大数据领域应用,运行于云原生环境中。然而,云原生计算与存储分离架构虽…...

软件测试--第十一章 设计和维护测试用例
1.单选题 (2分) 下面有关测试设计的叙述,说法不正确的是( )。 A 测试用例的设计是一项技术性强.智力密集型的活动 B 在开展测试用例设计前,必须将测试需求进行详细展开 C 在一般的测试组织内,测试用例的评审可能不是正式的评审会 D 在测试用例设计时,只设计覆盖正常流程和操…...

前端只允许一次函数调用
如果你正在进行前端开发,并且只想允许一次函数调用,你可以使用JavaScript的闭包结构创建一个只能被调用一次的函数。这样的函数有时被称为单次调用函数(“one-time call” functions)或一次性函数(“once” functions&…...

visdom使用时所遇的问题及解决方法
最近在用visdom进行可视化的过程中,虽然可有效的避免主机拒绝访问(该问题的解决方法,请参考深度学习可视化工具visdom使用-CSDN博客)即在终端输入python -m visom.server 1.训练过程中visdom出现ValueError: too many file descr…...
)
密封类(sealed class)
在 Kotlin 中,密封类(sealed class)是一种受限的类层次结构,允许您定义一个封闭的类层次结构,其中类的所有可能子类都已知并且位于同一文件中。密封类的主要作用是提供类型安全的受限层次结构,使得 when 表…...
私域引流宝PHP源码 以及搭建教程
私域引流宝PHP源码 以及搭建教程...
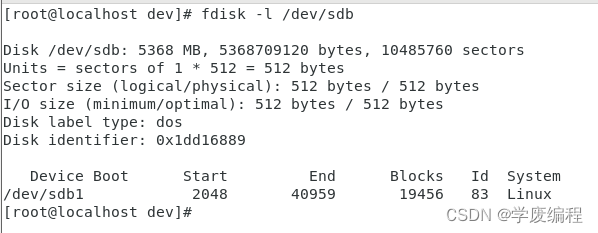
磁盘管理 以及磁盘的分区 详细版
磁盘管理 track:磁道,就是磁盘上同心圆,从外向里,依次1号、2号磁道sector:扇区,将磁盘分成一个一个扇形区域,每个扇区大小是512字节,从外向里,依次是1号扇区、2号扇区cylinder&…...

加码多肤色影像技术 这是传音找到的“出海利器“?
全球化时代,市场竞争愈演愈烈,产品差异化已然成为了企业脱颖而出的关键。在黄、白肤色长期占据人像摄影主赛道的背景下,传音就凭借独一无二的多肤色影像技术走出非洲,走向了更广阔的新兴市场。 聚焦深肤色人群拍照痛点,…...

C++方法封装成dll及C#调用示例
1,编译生成dll时可能出现错误,解决办法:pch.h文件头部,添加声明 #define _CRT_SECURE_NO_WARNINGS 2, c头文件声明 extern "C" __declspec(dllexport) char* getvalue(const char * param1, const char * param2); 3, c方法实现…...

定时清理Linux服务器缓存shell脚本
服务器内存占用过高,如何定时清理一下服务器内存呢?写一个清理缓存脚本,加入到定时任务中。 一、编写脚本 clear_cache.sh 脚本,放到home目录下。 #!/bin/bash# 清除页面缓存、目录项和 inode 缓存 sudo sync echo 3 | sudo tee /proc/sys/vm/drop_caches# 记录执行时间到日…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...

DingDing机器人群消息推送
文章目录 1 新建机器人2 API文档说明3 代码编写 1 新建机器人 点击群设置 下滑到群管理的机器人,点击进入 添加机器人 选择自定义Webhook服务 点击添加 设置安全设置,详见说明文档 成功后,记录Webhook 2 API文档说明 点击设置说明 查看自…...

并发编程 - go版
1.并发编程基础概念 进程和线程 A. 进程是程序在操作系统中的一次执行过程,系统进行资源分配和调度的一个独立单位。B. 线程是进程的一个执行实体,是CPU调度和分派的基本单位,它是比进程更小的能独立运行的基本单位。C.一个进程可以创建和撤销多个线程;同一个进程中…...

Spring Security 认证流程——补充
一、认证流程概述 Spring Security 的认证流程基于 过滤器链(Filter Chain),核心组件包括 UsernamePasswordAuthenticationFilter、AuthenticationManager、UserDetailsService 等。整个流程可分为以下步骤: 用户提交登录请求拦…...

GraphQL 实战篇:Apollo Client 配置与缓存
GraphQL 实战篇:Apollo Client 配置与缓存 上一篇:GraphQL 入门篇:基础查询语法 依旧和上一篇的笔记一样,主实操,没啥过多的细节讲解,代码具体在: https://github.com/GoldenaArcher/graphql…...
