KVM+GFS高可用
资源列表
| 操作系统 | IP | 主机名 |
| Centos7 | 192.168.10.51 | gfs1 |
| Centos7 | 192.168.10.52 | gfs2 |
| Centos7 | 192.168.10.53 | kvm |
在gfs节点部署GlusterFS
#添加hosts解析
cat >> /etc/hosts << EOF
192.168.10.51 gfs1
192.168.10.52 gfs2
192.168.10.53 kvm
EOF挂载磁盘分区(在gfs节点)
fdisk /dev/sdb
mkfs.xfs /dev/sdb1
mkdiir /data
mount /dev/sdb1 /data下载启动gfs
yum -y install centos-release-gluster
yum -y install glusterfs glusterfs-server glusterfs-fuse glusterfs-rdma
systemctl start glusterd.service
systemctl enable glusterd.service加入集群
gluster peer probe gfs1
gluster peer probe gfs2创建分布式复制卷
gluster volume create dis-dist replica 2 transport tcp gfs1:/data gfs2:/data
gluster volume start dis-dist
gluster volume info dis-dist在kvm挂载分布式复制卷
mkdir -p /data/{store,iso}
mount -t glusterfs gfs1:dis-dist /data
df -Th
gfs1:dis-dist fuse.glusterfs 20.0 147M 7.9G 2% /data
#永久挂载
echo 'gfs1:rep-volume /data glusterfs defaults,_netdev 0 0' >> /etc/fstab部署kvm虚拟机
#勾选处理器下的虚拟化
#检查是否支持虚拟化
grep -e 'vmx' -e 'svm' /proc/cpuinfo
#VMX是英特尔版本,SVM是AMD版本#检查KVM模块是否安装
lsmod |grep KVM下载kvm服务
yum -y install qemu-kvm qemu-kvm-tools qemu-img bridge-utils libvirt virt-install virt-manager virt-viewer
systemctl start libvirtd
systemctl enable libvirtd配置桥接模式
cd /etc/sysconfig/network-scripts/
cp ifcfg-ens33 ifcfg-br0#修改ens33网卡配置文件
echo 'BRIDGE=br0' >> ifcfg-ens33#修改br0配置文件
vim ifcfg-br0#删除UUID
TYPE=Bridge
NAME=br0
DEVICE=br0systemctl restart network创建虚拟机
#上传Centos镜像至/data/iso
[root@localhost ~]# ls /data/iso/
CentOS-7-x86_64-DVD-2207-02.isovirt-install \
--name test01 \
--ram 1024 \
--vcpus 1 \
--disk path=/data/store/test01.qcow2,size=10 \
--network bridge=br0 \
--virt-type kvm \
--accelerate \
--autostart \
--cdrom /data/iso/CentOS-7-x86_64-DVD-2207-02.iso \
--graphics vnc,port=5901,listen=0.0.0.0在其他两台机器查看/data也会有虚拟机文件
相关文章:

KVM+GFS高可用
资源列表 操作系统 IP 主机名 Centos7 192.168.10.51 gfs1 Centos7 192.168.10.52 gfs2 Centos7 192.168.10.53 kvm 在gfs节点部署GlusterFS #添加hosts解析 cat >> /etc/hosts << EOF 192.168.10.51 gfs1 192.168.10.52 gfs2 192.168.10.53 kvm EOF …...

C++迈向精通:当我尝试修改虚函数表
尝试修改虚函数表 本期纯整活儿好吧!!!! 初衷 有一天我突然开始好奇虚函数表是否真的存在,于是我开始想是否能够从C中查看或者调用虚函数表中的内容。,于是有了下面的操作。 操作过程 起初我并没有思路…...
IDEA 高效插件工具
文章目录 LombokMaven Helper 依赖冲突any-rule(正则表达式插件)快速生成javadocGsonFormat (Aits) 将json解析成类Diagrams使用 类图SequenceDiagram时序图GenerateAllSetter(AltEnter)大小写转写String ManipulationGitToolBox 代码提交人activate-pow…...

SQL入门大全
SQL(Structured Query Language,结构化查询语言)是一种用于管理关系型数据库的标准编程语言。它具有数据操纵和数据定义等多种功能,为数据库管理系统提供了强大的交互性特点,能够极大地提高计算机应用系统的工作质量与…...

【深度优先搜索 广度优先搜索】297. 二叉树的序列化与反序列化
本文涉及知识点 深度优先搜索 广度优先搜索 深度优先搜索汇总 图论知识汇总 LeetCode297. 二叉树的序列化与反序列化 序列化是将一个数据结构或者对象转换为连续的比特位的操作,进而可以将转换后的数据存储在一个文件或者内存中,同时也可以通过网络传…...
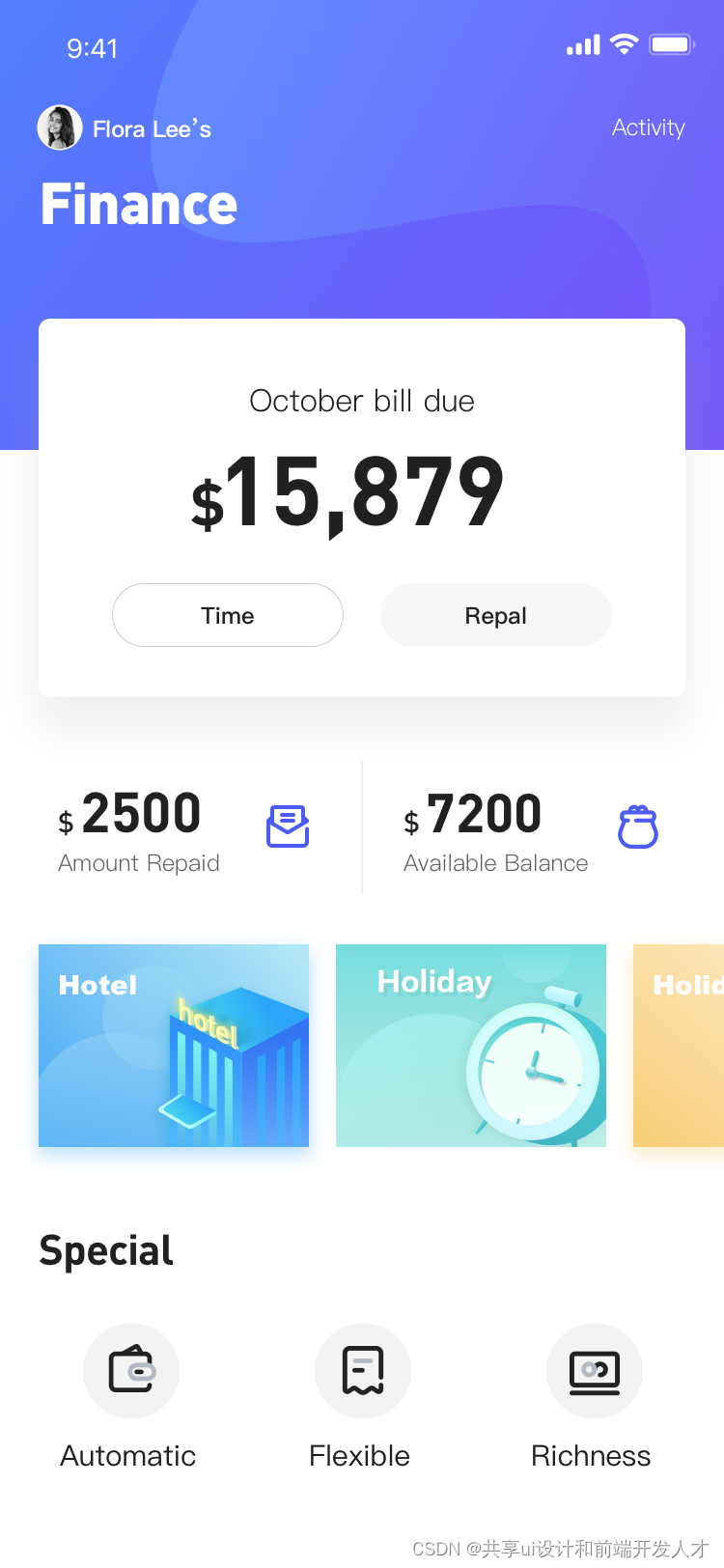
App UI 风格,引领设计风向
App UI 风格,引领设计风向...
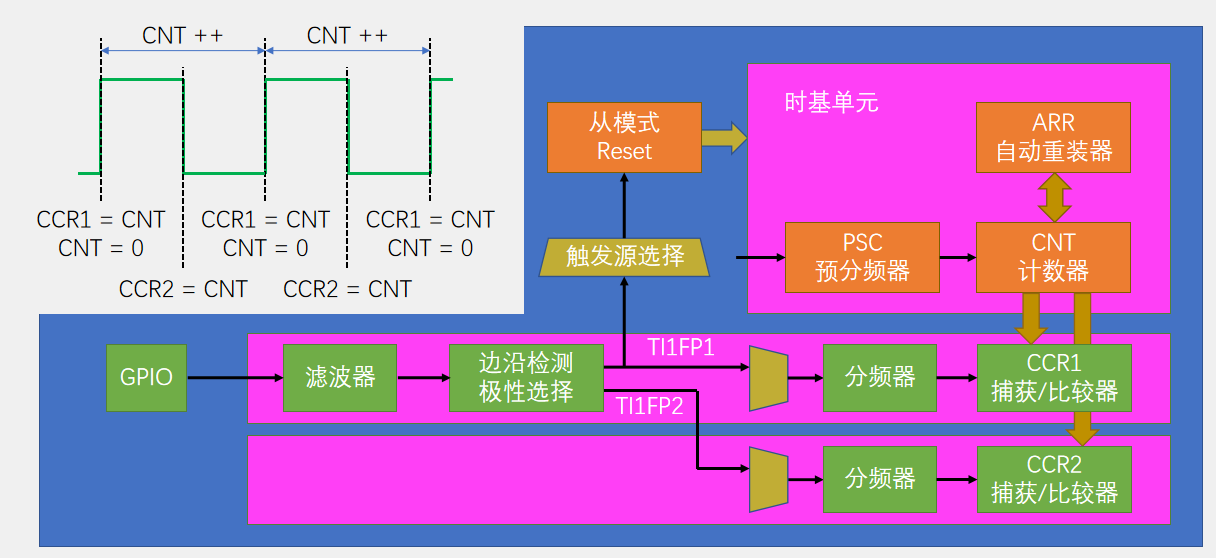
TIM—通用定时器高级定时器
通用/高级定时器的功能 在基本定时器功能的基础上新增功能: 通用定时器有4个独立通道,且每个通道都可以用于下面功能。 (1)输入捕获:测量输入信号的周期和占空比等。 (2)输出比较:产…...
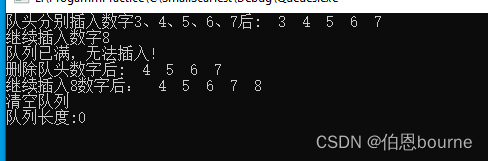
【数据结构与算法(C语言)】循环队列图解
目录 1. 前言1.1 普通循环队列假溢出1.1.1 初始化队列1.1.2 插满队列1.1.3 删除元素后,再插入元素 1.2 循环队列1.2.1 插入元素,队列已满1.2.2 将元素J1、J2出列,循环队列又空出两个空间1.2.3 元素J6可以继续入列 2. 存储结构和函数说明2.1 队…...

私域流量转化不济的原因
你是不是也曾感到私域流量的转化一直不如意?让我来告诉你,这六大问题是为什么,以及如何轻松解决它们,提升你的私域流量转化率! 1. 问题:目标不明确 你是否常常感到茫然,不知道私域流量应该有何目…...

百万上下文RAG,Agent还能这么玩
❝ 在AI技术飞速发展的今天,我们见证了许多令人惊叹的突破。最近,Qwen2模型的开源引起了广泛的关注,它不仅展示了超越闭源模型的能力,还带来了一个全新的框架——Qwen-Agent。 Qwen-Agent的设计思路虽然与LangChain相似࿰…...
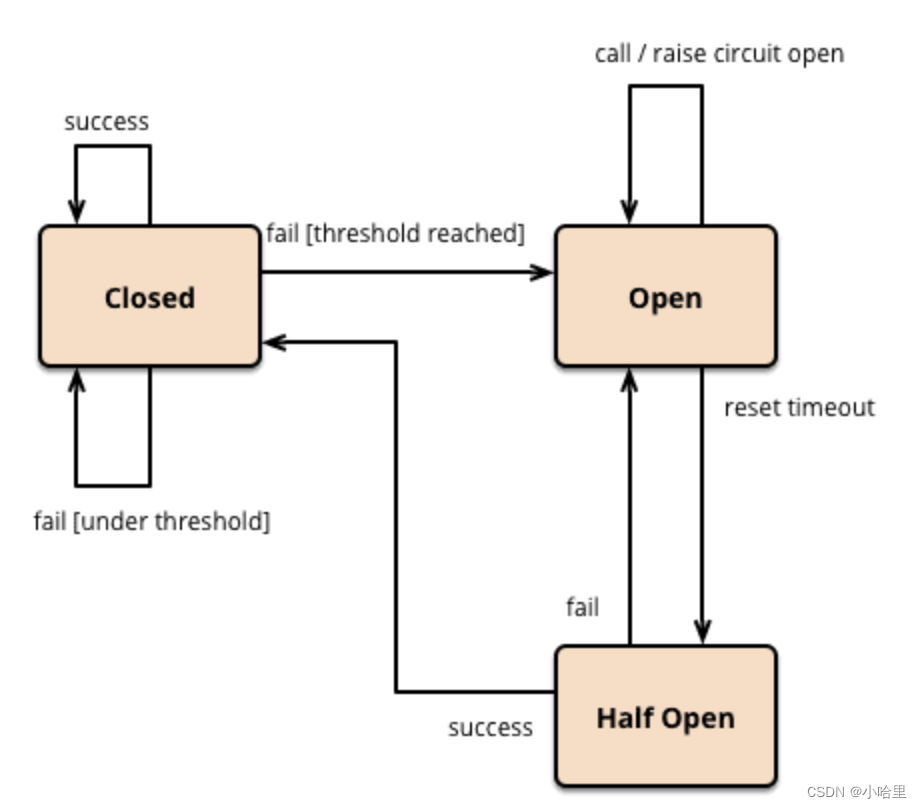
【后端开发】服务开发场景之高可用(冗余设计,服务限流,降级熔断,超时重试,性能测试)
【后端开发】服务开发场景之高可用(冗余设计,服务限流,降级熔断,超时重试,性能测试) 文章目录 序:如何设计一个高可用的系统?可用性的判断指标是什么?哪些情况会导致系统…...
在 Selenium 中更改 User-Agent | 步骤与最佳实践
在 Selenium 中更改 User Agent 是许多网页抓取任务中的关键步骤。它有助于将自动化脚本伪装成常规浏览器,从而避免被网站检测到。本指南将带您了解如何在 Selenium 中更改 Google Chrome 的 User Agent,并提供最佳实践以确保您的网页抓取任务顺利进行。…...
2024酒店IPTV云桌面系统建设方案
Hello大家好,我是点量小芹,这一年多的时间一直在分享实时云渲染像素流相关的内容,今天和大家聊聊酒店IPTV云桌面电视系统解决方案,或者有的朋友也会称之为IPTV服务器。熟悉小芹的朋友知道,IPTV软件系统是我们一直在推的…...

java Thrift TThreadPoolServer 多个processor 的实现
当我们使用Thrift 通信的时候,服务端有时候需要注册多个类,去实现通信,这时候我们就不能再使用单一Processor的方式,就要使用多个Processor,那么如何去实现呢? 多个Process 服务端 public static void m…...

失眠焦虑的解脱之道:找回内心的平静
🍃 在这个快节奏的时代,失眠与焦虑似乎成了许多人的隐形敌人。每当夜幕降临,它们便悄悄潜入心底,扰乱我们的思绪,让宁静的夜晚变得无比漫长。然而,生活总有办法让我们找回内心的平静,只需稍作调…...

OLED柔性屏的显示效果如何
OLED柔性屏的显示效果非常出色,具有多方面的优势。以下是关于OLED柔性屏显示效果的详细分析: 色彩表现:OLED柔性屏的每个像素都可以独立发光,因此色彩准确性极高。黑色呈现得非常深邃,而亮部则展现出鲜明而生动的细节。…...

百货商城优选 伊利牛奶推出全国首款减甲烷环保学生奶
近日,伊利集团受邀参加在全国首个“国际首脑峰会零碳场馆”召开的“降碳增产科技助力奶业绿色高质量发展”首款低碳饲料创新大会。会上,伊利宣布将推出全国首款减甲烷环保学生牛奶——伊利QQ星学生纯牛奶,进一步将可持续发展落到实处…...

Fluid 1.0 版发布,打通云原生高效数据使用的“最后一公里”
作者:顾荣 前言 得益于云原生技术在资源成本集约、部署运维便捷、算力弹性灵活方面的优势,越来越多企业和开发者将数据密集型应用,特别是 AI 和大数据领域应用,运行于云原生环境中。然而,云原生计算与存储分离架构虽…...

软件测试--第十一章 设计和维护测试用例
1.单选题 (2分) 下面有关测试设计的叙述,说法不正确的是( )。 A 测试用例的设计是一项技术性强.智力密集型的活动 B 在开展测试用例设计前,必须将测试需求进行详细展开 C 在一般的测试组织内,测试用例的评审可能不是正式的评审会 D 在测试用例设计时,只设计覆盖正常流程和操…...

前端只允许一次函数调用
如果你正在进行前端开发,并且只想允许一次函数调用,你可以使用JavaScript的闭包结构创建一个只能被调用一次的函数。这样的函数有时被称为单次调用函数(“one-time call” functions)或一次性函数(“once” functions&…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...
