AcWing 477:神经网络 ← 拓扑排序+链式前向星
【题目来源】
https://www.acwing.com/problem/content/479/
【题目描述】
人工神经网络(Artificial Neural Network)是一种新兴的具有自我学习能力的计算系统,在模式识别、函数逼近及贷款风险评估等诸多领域有广泛的应用。
对神经网络的研究一直是当今的热门方向,兰兰同学在自学了一本神经网络的入门书籍后,提出了一个简化模型,他希望你能帮助他用程序检验这个神经网络模型的实用性。
在兰兰的模型中,神经网络就是一张有向图,图中的节点称为神经元,而且两个神经元之间至多有一条边相连,下图是一个神经元的例子:

图中,X1—X3是信息输入渠道,Y1-Y2 是信息输出渠道,C1 表示神经元目前的状态,Ui 是阈值,可视为神经元的一个内在参数。
神经元按一定的顺序排列,构成整个神经网络。
在兰兰的模型之中,神经网络中的神经元分为几层;称为输入层、输出层,和若干个中间层。
每层神经元只向下一层的神经元输出信息,只从上一层神经元接受信息。
下图是一个简单的三层神经网络的例子。

兰兰规定,Ci 服从公式:,(其中 n 是网络中所有神经元的数目)
公式中的Wji(可能为负值)表示连接 j 号神经元和 i 号神经元的边的权值。
当 Ci 大于 0 时,该神经元处于兴奋状态,否则就处于平静状态。
当神经元处于兴奋状态时,下一秒它会向其他神经元传送信号,信号的强度为 Ci。
如此.在输入层神经元被激发之后,整个网络系统就在信息传输的推动下进行运作。
现在,给定一个神经网络,及当前输入层神经元的状态(Ci),要求你的程序运算出最后网络输出层的状态。
【输入格式】
输入文件第一行是两个整数 n 和 p。
接下来 n 行,每行两个整数,第 i+1 行是神经元 i 最初状态和其阈值(Ui)。注意:输入层给定的状态即为最终值,不需要再减去 Ui,非输入层的神经元开始时状态必然为 0。
再下面 P 行,每行有两个整数 i,j 及一个整数 Wij,表示连接神经元 i、j 的边权值为 Wij。
【输出格式】
输出文件包含若干行,每行有两个整数,分别对应一个神经元的编号,及其最后的状态,两个整数间以空格分隔。
仅输出最后状态大于零的输出层神经元状态,并且按照编号由小到大顺序输出。
若输出层的神经元最后状态都不大于零,则输出 NULL。
【数据范围】
1≤n≤100
【输入样例】
5 6
1 0
1 0
0 1
0 1
0 1
1 3 1
1 4 1
1 5 1
2 3 1
2 4 1
2 5 1
【输出样例】
3 1
4 1
5 1
【算法分析】
● 拓扑序列:https://blog.csdn.net/hnjzsyjyj/article/details/129811447
● 链式前向星:https://blog.csdn.net/hnjzsyjyj/article/details/139369904
val[idx]:存储编号为 idx 的边的值
e[idx]:存储编号为 idx 的结点的值
ne[idx]:存储编号为 idx 的结点指向的结点的编号
h[a]:存储头结点 a 指向的结点的编号
【算法代码】
#include <bits/stdc++.h>
using namespace std;const int maxn=105;
const int maxm=maxn*maxn/2;
int val[maxm],e[maxn],ne[maxn],h[maxn],idx;
int f[maxn],u[maxn],din[maxn],dout[maxn];
int q[maxn];
int n,m;void add(int a,int b,int w) {val[idx]=w,e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}void topsort() {int hh=0, tt=-1;for(int i=1; i<=n; i++)if(!din[i]) q[++tt]=i;while(hh<=tt) {int t=q[hh++];for(int i=h[t]; i!=-1; i=ne[i]) {int j=e[i];if(--din[j]==0) q[++tt]=j;}}
}int main() {cin>>n>>m;for(int i=1; i<=n; i++) {cin>>f[i]>>u[i];if(!f[i]) f[i]-=u[i];}memset(h,-1,sizeof h);while(m--) {int a,b,c;cin>>a>>b>>c;add(a,b,c);dout[a]++;din[b]++;}topsort();for(int i=0; i<n; i++) {int j=q[i];if(f[j]>0) {for(int k=h[j]; k!=-1; k=ne[k])f[e[k]]+=f[j]*val[k];}}bool flag=true;for(int i=1; i<=n; i++)if(!dout[i] && f[i]>0) {cout<<i<<" "<<f[i]<<endl;flag=false;}if(flag) cout<<"NULL"<<endl;return 0;
}/*
in:
5 6
1 0
1 0
0 1
0 1
0 1
1 3 1
1 4 1
1 5 1
2 3 1
2 4 1
2 5 1out:
3 1
4 1
5 1
*/
【参考文献】
https://www.acwing.com/solution/content/3706/
https://blog.csdn.net/hnjzsyjyj/article/details/139369904
https://blog.csdn.net/hnjzsyjyj/article/details/129811447
相关文章:
AcWing 477:神经网络 ← 拓扑排序+链式前向星
【题目来源】https://www.acwing.com/problem/content/479/【题目描述】 人工神经网络(Artificial Neural Network)是一种新兴的具有自我学习能力的计算系统,在模式识别、函数逼近及贷款风险评估等诸多领域有广泛的应用。 对神经网络的研究…...

鲁教版八年级数学下册-笔记
文章目录 第六章 特殊平行四边形1 菱形的性质与判定2 矩形的性质与判定3 正方形的性质与判定 第七章 二次根式1 二次根式2 二次根式的性质3 二次根式的加减二次根式的乘除 第八章 一元二次方程1 一元二次方程2 用配方法解一元二次方程3 用公式法解一元二次方程4 用因式分解法解…...

Web前端栅格:深入解析与实战应用
Web前端栅格:深入解析与实战应用 在Web前端开发中,栅格系统是一种重要的布局工具,它能够帮助我们快速构建响应式、灵活且美观的页面布局。然而,对于许多初学者和从业者来说,栅格系统的概念、原理以及实际应用却常常令…...

mysql Innodb引擎常见问题
问题 1:InnoDB 引擎的主要特点有哪些? 答:支持事务、行级锁、外键约束,具有较好的数据完整性和并发性。 问题 2:InnoDB 如何实现事务的 ACID 特性? 答:通过原子性(事务要么全部成功要…...
创建 MFC DLL-使用关键字_declspec(dllexport)
本文仅供学习交流,严禁用于商业用途,如本文涉及侵权请及时联系本人将于及时删除 从MFC DLL中导出函数的另一种方法是在定义函数时使用关键字_declspec(dllexport)。这种情况下,不需要DEF文件。 导出函数的形式为: declspec(dll…...
机器学习笔记 - 用于3D数据分类、分割的Point Net的网络实现
上一篇,我们大致了解了Point Net的原理,这里我们要进行一下实现。 机器学习笔记 - 用于3D数据分类、分割的Point Net简述-CSDN博客文章浏览阅读3次。在本文中,我们将了解Point Net,目前,处理图像数据的方法有很多。从传统的计算机视觉方法到使用卷积神经网络到Transforme…...

C#知识|基于实体类对象,返回实体集合封装介绍。
哈喽,你好啊,我是雷工! 前面通过实体类封装传递了零散的参数,打包后给数据访问方法。 但当查询结果是数据集,要把查询到的数据返回给UI时,我们也可以把返回的多条零散数据封装到实体类中。 此次练习可以使用实体容器:泛型集合List<T>,当把每条数据封装成实体对…...
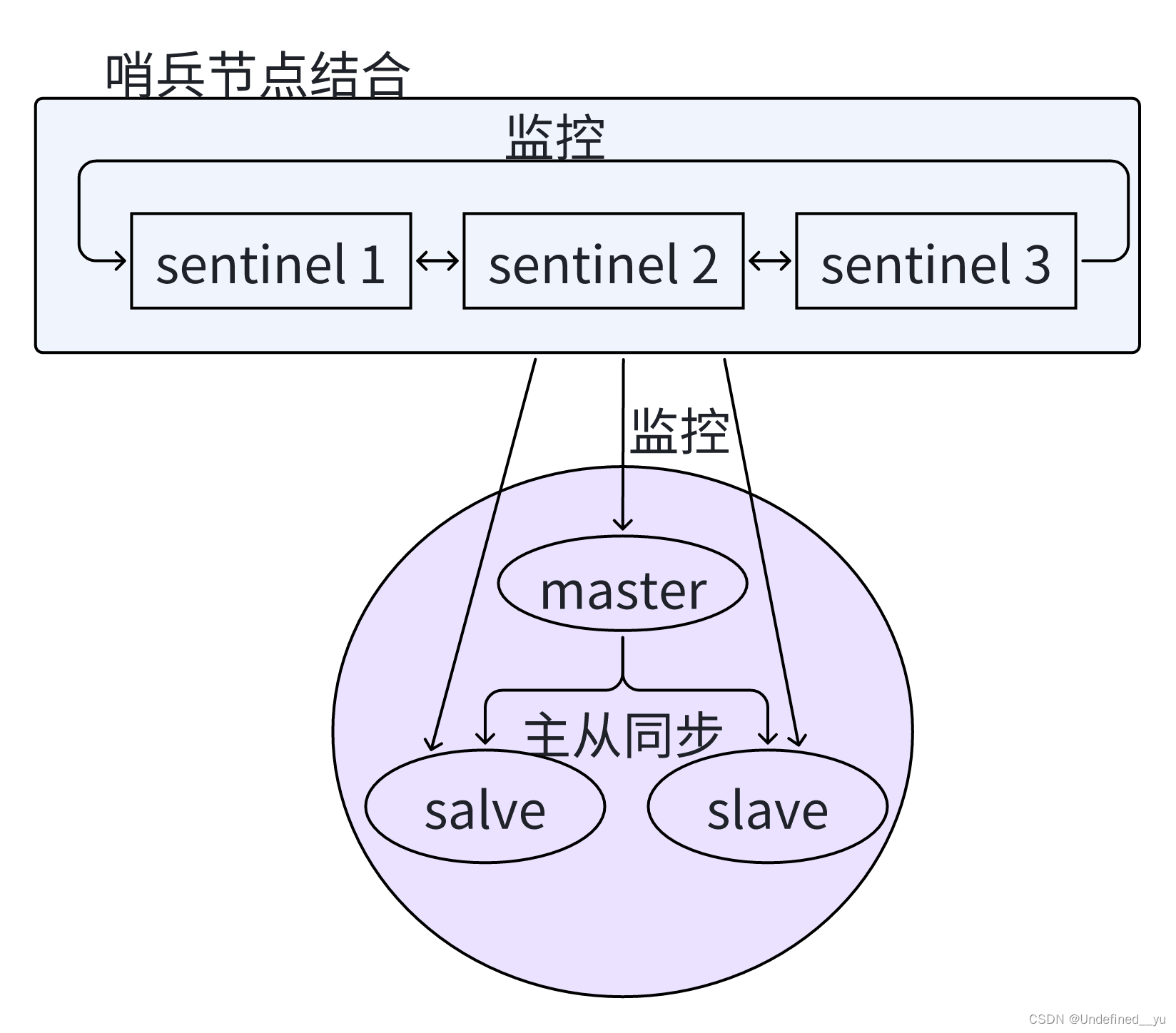
关于Redis中哨兵(Sentinel)
Redis Sentinel 相关名词解释 名词 逻辑结构 物理结构 主节点 Redis 主服务 一个独立的 redis-server 进程 从节点 Redis 从服务 一个独立的 redis-server 进程 Redis 数据节点 主从节点 主节点和从节点的进程 哨兵节点 监控 Redis 数据节点的节点 一个独立的 re…...

论文阅读:H-ViT,一种用于医学图像配准的层级化ViT
来自CVPR的一篇文章,用CNNTransformer混合模型做图像配准。可变形图像配准是一种在相同视场内比较或整合单模态或多模态视觉数据的技术,它旨在找到两幅图像之间的非线性映射关系。 1,模型结构 首先,使用类似特征金字塔网络&#…...
【MySQL】(基础篇七) —— 通配符和正则表达式
通配符和正则表达式 本章介绍什么是通配符、如何使用通配符以及怎样使用LIKE操作符进行通配搜索,以便对数据进行复杂过滤;如何使用正则表达式来更好地控制数据过滤。 目录 通配符和正则表达式LIKE操作符百分号(%)通配符下划线(_)通配符 通配符使用技巧正…...

HTML静态网页成品作业(HTML+CSS)—— 名人霍金介绍网页(6个页面)
🎉不定期分享源码,关注不丢失哦 文章目录 一、作品介绍二、作品演示三、代码目录四、网站代码HTML部分代码 五、源码获取 一、作品介绍 🏷️本套采用HTMLCSS,未使用Javacsript代码,共有6个页面。 二、作品演示 三、代…...
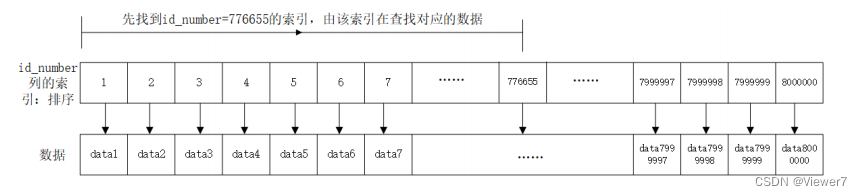
MySQL: 索引与事务
文章目录 1. 索引 (Index)1.1 概念1.2 作用1.3 使用场景1.4 索引的使用1.5 索引的使用案例 (不要轻易尝试)1.6 索引背后的数据结构1.7 重点总结 2.事务2.1 为什么要使用事务2.2 事务的概念2.3 事务的使用2.4 对事务的理解2.5 事务的基本特性 1. 索引 (Index) 1.1 概念 索引是…...

2024年最新Microsoft Edge关闭自动更新的方法分享
这里写自定义目录标题 打开【服务】 打开【服务】 windows中搜索服务,如下图: 打开服务界面,找到“Microsoft Edge Update Service (edgeupdate)” 及 “Microsoft Edge Update Service (edgeupdatem)” 两个服务,设置为禁用...

Unity3D TextMeshPro组件使用及优化详解
在Unity3D游戏开发中,文本渲染是一个不可或缺的部分。而TextMeshPro作为Unity的一个插件,提供了更高质量、更灵活的文本渲染功能,为开发者带来了极大的便利。本文将详细介绍TextMeshPro组件的使用技巧以及优化方法,并通过代码实例…...

react 0至1 【jsx】
1.函数调用 // 项目的根组件 // App -> index.js -> public/index.html(root)const count 100function getName () {return test }function App () {return (<div className"App">this is App{/* 使用引号传递字符串 */}{this is message}{/* 识别js变…...

算法训练营day58
题目1:392. 判断子序列 - 力扣(LeetCode) 暴力解法 class Solution { public:bool isSubsequence(string s, string t) {if(s.size() > t.size()) return false;if(s.size() < t.size()) {swap(s, t);}bool reslut false;int flag …...

JAVA面试中,面试官最爱问的问题。
解释Java中的抽象类和接口的区别。 在Java中,抽象类和接口都是用来定义类的抽象行为和特性的,但它们有一些关键区别: ### 抽象类 1. **定义**:抽象类是使用abstract关键字修饰的类,不能被实例化,只能被继…...
分类算法与逻辑回归分类算法的差异与特性?)
【机器学习300问】115、对比K近邻(KNN)分类算法与逻辑回归分类算法的差异与特性?
在学习了K近邻(KNN)和逻辑回归(Logistic Regression)这两种分类算法后,对它们进行总结和对比很有必要。尽管两者都能有效地执行分类任务,但它们在原理、应用场景和性能特点上存在着显著的差异。本文就是想详…...

Selenium IDE 工具
官网 ## https://blog.csdn.net/weixin_49770443/article/details/129366721## https://www.selenium.dev/selenium-ide/是什么? Selenium IDE是 Selenium Suite 下的开源 Web 自动化测试工具。 Selenium IDE 一个用于火狐 (firefox) 浏览器的插件,打开…...

python的open函数
1.open() 1.1 参数11.2 参数21.3 参数32.with open() as 3.open函数常用的方法 3.1 读3.2 写3.3 获取文件读写类型3.4 指针移动3.5 当前指针位置3.6 truncate在python中使用open函数对文件进行处理。 1.open() python打开文件使用open()函数,返回一个指向文件的指针。该函数常…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...

LINUX 69 FTP 客服管理系统 man 5 /etc/vsftpd/vsftpd.conf
FTP 客服管理系统 实现kefu123登录,不允许匿名访问,kefu只能访问/data/kefu目录,不能查看其他目录 创建账号密码 useradd kefu echo 123|passwd -stdin kefu [rootcode caozx26420]# echo 123|passwd --stdin kefu 更改用户 kefu 的密码…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...

CRMEB 中 PHP 短信扩展开发:涵盖一号通、阿里云、腾讯云、创蓝
目前已有一号通短信、阿里云短信、腾讯云短信扩展 扩展入口文件 文件目录 crmeb\services\sms\Sms.php 默认驱动类型为:一号通 namespace crmeb\services\sms;use crmeb\basic\BaseManager; use crmeb\services\AccessTokenServeService; use crmeb\services\sms\…...

基于Springboot+Vue的办公管理系统
角色: 管理员、员工 技术: 后端: SpringBoot, Vue2, MySQL, Mybatis-Plus 前端: Vue2, Element-UI, Axios, Echarts, Vue-Router 核心功能: 该办公管理系统是一个综合性的企业内部管理平台,旨在提升企业运营效率和员工管理水…...
