【SCAU数据挖掘】数据挖掘期末总复习题库简答题及解析——上
1.K-Means
假定我们对A、B、C、D四个样品分别测量两个变量,得到的结果见下表。
| 样品 | 变量 | |
| X1 | X2 | |
| A | 5 | 3 |
| B | -1 | 1 |
| C | 1 | -2 |
| D | -3 | -2 |
利用K-Means方法将以上的样品聚成两类。为了实施均值法(K-Means)聚类,首先将这些样品随意分成两类(A、B)和(C、D)。请详细给出每次聚类的中心坐标,计算样品到中心坐标的欧氏平方距离。
解:
第一步:按要求取K=2,为了实施均值法聚类,我们将这些样品随意分成两类(A、B)和(C、D),然后计算这两个聚类的中心坐标(见下表)。中心坐标是通过原始数据计算得来的。
聚类中心坐标一
| 聚类 | 中心坐标 | |
| X1 | X2 | |
| (A、B) | 2 | 2 |
| (C、D) | -1 | -2 |
第二步:计算某个样品到各类中心的欧氏平方距离,然后将该样品分配给最近的一类对于样品有变动的类,重新计算它们的中心坐标,为下一步聚类做准备。先计算A到两个类的平方距离:
d²(A,(AB))=(5-2)²+(3-2)²=10
d²(A,(CD))= (5 + 1)²+ (3 + 2)²= 61
由于A到(4、B)的距离小于到(C、D)的距离,因此A不用重新分配。计算B到两类的平方距离
d²(B,(AB))=(-1-2)²+(1-2)²=10
d²(B,(CD))=(-1 + 1)²+(1 + 2)²=9
由于B到(4、B)的距离大于到(C、D)的距离,因此B要分配给(C、D)类,得到新的聚类是(A)和(B、C、D)。更新中心坐标如下表所示。
聚类中心坐标二
| 聚类 | 中心坐标 | |
| X1 | X2 | |
| (A) | 5 | 3 |
| (B、C、D) | -1 | -1 |
第三步:再次检查每个样品,以决定是否需要重新分类。计算各样品到各中心的距离平方,结果如下表所示。
样本到中心的距离平方
| 聚类 | 样本到中心的距离平方 | |||
| A | B | C | D | |
| (A) | 0 | 40 | 41 | 89 |
| (B、C、D) | 52 | 4 | 5 | 5 |
到现在为止,每个样品都已经分配给距离中心最近的类,聚类过程到此结束。最终得到K=2的聚类结果是4独自成一类,B、C、D聚成一类。
2.试分析回归与分类的区别。
| 输出结果 | 应用场景 | |
| 分类 | 离散的类别标签 (有限个离散变量) | 用于将事物或数据样本分配到一个或多个预定义的类别中,比如识别图片中的动物种类。分类的目标是构建一个模型,该模型能够基于输入的特征来预测数据样本所属的类别。 |
| 回归 | 连续的数值 (连续变量) | 通常用于预测一个连续性的数值,比如预测股票价格。目标是找到一个函数,能够基于输入的特征来预测一个连续的数值。 |
3.基于正态分布的离群点检测
假设某城市过去10年中7月份的平均温度按递增序排列,结果为24℃、28.9℃、28.9℃、29℃、29.1℃、29.1℃、29.2℃、29.2℃、29.3℃和29.4℃。假定平均温度服从正态分布,由两个参数决定:均值和标准差。假设数据分布在这个区间(以平均![]() 标准差)之外,该数据对象即为离群点。
标准差)之外,该数据对象即为离群点。
(1)利用最大似然估计求均值和标准差。
均值(μ)的估计:
其中 n=10,xi 是每个样本的温度值。
将给定的温度值代入公式,得到:
μ=(24+2×28.9+29+2×29.1+2×29.2+29.3+29.4)/10=28.61
标准差(σ)的估计:
由于样本数量 n=10,我们使用样本标准差的无偏估计: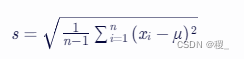
将给定的温度值和计算得到的均值代入公式,得到标准差 s 的值。
s=sqrt([(24-28.61)^2+(28.9-28.61)^2+...+(29.4-28.61)^2]/9)约等于1.63
(2)寻找上述10个对象中的所有离群点。
根据题目,离群点定义为数据对象落在平均值加减一个标准差之外的值。即,离群点不在区间
(μ^−σ^,μ^+σ^)=(28.61−1.63,28.61+1.63)=(26.98,30.24) 内。
由于 μ=28.61 和 s≈1.63,我们可以发现所有给定的温度值中24℃不在区间 (26.98,30.24) 内。
4.K均值与K中心点
K均值和K中心点算法都可以进行有效的聚类。
(1)概述K均值和K中心点的优缺点。
| 优点 | 缺点 | |
| K均值法 | 聚类时间短。当结果簇密集且簇间区别明显,效果较好。能对大数据集进行高效划分。 | 必须先指定聚类簇的个数。只适用于数值属性聚类,对噪声和异常数据很敏感,对于不同的初始值,结果可能不同。不适合发现非凸面形状的簇。 |
| K中心点法 | 对于非凸数据集也能较好聚类效果,且对于噪声点影响比较小 | 算法效率相对K-均值法较低,还有可能出现簇中心点初始化不佳,导致聚类结果不埋想的情况。 |
(2)概述这两种方法与层次聚类方法相比较有何优缺点。
层次聚类方法(AGNES)是一种分层聚类的方法,将教据点分层次进行聚类,也就是在保留所有数据点的前提下,从最小单元开始进行聚类,然后逐步合并相近的类别,最后形成n个。
优点是没有预先设定需要聚类的数量,能够处理复杂的数据结构,相对于K-均值、K-中心点更能反映出数据分布的全貌,尤其是在不平凡分布的数据上表现更加突出。
缺点是AGNES算法计算量较大,在大规模数据集上效率较低,且聚类结果可能受到簇合并顺序的影响。
5.Apriori算法:通过限制候选产生发现频繁项集
数据表中有5个事物,设min_sup=60%,min_conf=80%,并有下表所示信息。
| TID | 购买的商品 |
| T100 | {M,O,N,K,E,Y} |
| T200 | {D,O,N,K,E,Y} |
| T300 | {M,A,K,E} |
| T400 | {M,U,C,K,Y} |
| T500 | {C,O,O,K,I,E} |
请用Apriori算法找出频繁项集。
置信度(min_conf)是在找到频繁项集之后,用于生成关联规则时的一个参数,不用理会。
依题得min_sup=0.6*5=3,计算所有单项集的计数得到支持度计数大于等于3的频繁1-项集:
m 3
o 3
n 2
k 5
e 4
y 3
d 1
a 1
u 1
c 2
i 1
频繁 1- 顶集: M,O,K,E,Y
然后根据频繁1-项集,找出支持度技术大于等于3的频繁2-项集:
mo 1
mk 3
me 2
my 2
ok 3
oe 3
oy 2
ke 4
ky 3
ey 2
频繁 2- 项集: {M,K},{O,K},{O,E} ,{K,Y},{K,E}
再根据频繁2-项集,找出支持度技术大于等于3的频繁3-项集:
oke 3
key 2
频繁 3- 项集: {O,K,E}
故,用Apriori算法找出的频繁项集有频繁 1- 顶集: M,O,K,E,Y; 频繁 2- 项集: {M,K},{O,K},{O,E} ,{K,Y},{K,E}; 频繁 3- 项集: {O,K,E}
相关文章:
【SCAU数据挖掘】数据挖掘期末总复习题库简答题及解析——上
1.K-Means 假定我们对A、B、C、D四个样品分别测量两个变量,得到的结果见下表。 样品 变量 X1X2 A 5 3 B -1 1 C 1 -2 D -3 -2 利用K-Means方法将以上的样品聚成两类。为了实施均值法(K-Means)聚类,首先将这些样品随意分成两类(A、B)和(C、…...

云时代的Java:在云环境中实施Java的最佳实践
引言 云计算已经成为现代软件开发不可或缺的一部分,它提供了灵活性、可扩展性和成本效益。对于Java开发者来说,掌握在云环境中部署和管理Java应用的最佳实践是至关重要的。本文将探讨一些关键策略,帮助你最大化Java在云平台上的性能和效率。…...

STL - 常用算法
概述: 算法主要是由头文件<algorithm><functional><numeric>组成<algorithm>是所有STL头文件中最大的一个,范围涉及比较、 交换、查找、遍历操作、复制、修改等等<numeric>体积很小,只包括几个在序列上面进行…...
)
Qt | QTextStream 类(文本流)
01、字符编码 1、怎样将字符转换为二进制形式进行存储,存在一个编码的问题,通常都需进行两次编码, 2、字符集:字符的第一次编码是将字符编码为与一个数值(如一个 10 进制整数)相对应,比如把字符 A 编码为 10 进制的 65,B 编码为 66 等。把每一个字符都编码为与一个数值…...

Python学习笔记7:入门知识(七)
前言 之前说过我更换了新的学习路线,现在是根据官方文档和书籍Python crash course来进行学习的,在目前的学习中,对于之前的知识有一些遗漏,这里进行补充。 学习资料有两个,书籍中文版PDF,关注我私信发送…...

如何翻译和本地化游戏?翻译访谈
如何翻译和本地化游戏?这个过程的技术细节有哪些?游戏翻译不同于电影翻译。Logrus IT游戏本地化部门负责人阿列克谢费奥多罗夫(Alexey Fedorov)在接受RUDN语言学系外语系教授和研究人员的采访时谈到了这一点,他是由尤利…...

[C++] 从零实现一个ping服务
💻文章目录 前言ICMP概念报文格式 Ping服务实现系统调用函数具体实现运行测试 总结 前言 ping命令,因为其简单、易用等特点,几乎所有的操作系统都内置了一个ping命令。如果你是一名C初学者,对网络编程、系统编程有所了解ÿ…...

2024网络安全学习路线 非常详细 推荐学习
关键词:网络安全入门、渗透测试学习、零基础学安全、网络安全学习路线 首先咱们聊聊,学习网络安全方向通常会有哪些问题 1、打基础时间太长 学基础花费很长时间,光语言都有几门,有些人会倒在学习 linux 系统及命令的路上&#…...
STM32F103ZET6_HAL_CAN
1定义时钟 2定义按键 按键上拉电阻 3开启串口 4打开CAN(具体什么意思上一篇讲了) 5生成代码 /* USER CODE BEGIN Header */ /********************************************************************************* file : main.c* brief …...

javaWeb项目-ssm+vue网上租车系统功能介绍
本项目源码:java-基于ssmvue的网上租车系统源码说明文档资料资源-CSDN文库 项目关键技术 开发工具:IDEA 、Eclipse 编程语言: Java 数据库: MySQL5.7 框架:ssm、Springboot 前端:Vue、ElementUI 关键技术:springboot、…...
Go模板页面浏览器显示HTML源码问题
<!--* Title: This is a file for ……* Author: JackieZheng* Date: 2024-06-09 17:00:01* LastEditTime: 2024-06-09 17:01:12* LastEditors: Please set LastEditors* Description:* FilePath: \\GoCode\\templates\\index.html --> <!DOCTYPE html> <html …...
弃用Docker Desktop:在WSL2中玩转Docker之Docker Engine 部署与WSL入门
Docker技术概论 在WSL2中玩转Docker之Docker Engine部署 - 文章信息 - Author: 李俊才 (jcLee95) Visit me at CSDN: https://jclee95.blog.csdn.netMy WebSite:http://thispage.tech/Email: 291148484163.com. Shenzhen ChinaAddress of this article:https://bl…...

Mac下载了docker,在终端使用docker命令时用不了
问题:在mac使用docker的时候,拉取docker镜像失败 原因:docker是需要用app使用的 ,所以在使用的时候必须打开这个桌面端软件才可以在终端上使用docker命令!!!...
Spring Security——基于MyBatis
目录 项目总结 新建一个项目 pom.xml application.properties配置文件 User实体类 UserMapper映射接口 UserService访问数据库中的用户信息 WebSecurityConfig配置类 MyAuthenticationFailureHandler登录失败后 MyAuthenticationSuccessHandlerw登录成功后 WebSecur…...
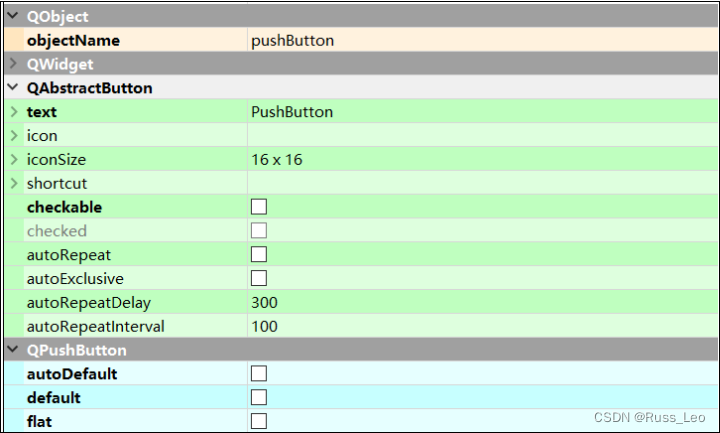
Qt——升级系列(Level Four):控件概述、QWidget 核心属性、按钮类控件
目录 控件概述 QWidget 核心属性 核心属性概览 enabled geometry windowTitle windowIcon windowOpacity cursor font toolTip focusPolicy styleSheet 按钮类控件 Push Button Radio Buttion Check Box Tool Button 控件概述 Widget 是 Qt 中的核⼼概念. 英⽂原义是 "…...
品质卓越为你打造App UI 风格
品质卓越为你打造App UI 风格...

ei期刊和sci期刊的区别
ei期刊和sci期刊的区别 ei期刊和sci期刊的区别是什么?Sci和ei都属于国际期刊的一种,但是二者之间存在一些区别,选择期刊投稿时需要注意这些区别。EI期刊刊物的审查周期短,SCI学术期刊的审查期长。难度要求不同,SCI期刊比EI期刊对…...

从零手写实现 nginx-20-placeholder 占位符 $
前言 大家好,我是老马。很高兴遇到你。 我们为 java 开发者实现了 java 版本的 nginx https://github.com/houbb/nginx4j 如果你想知道 servlet 如何处理的,可以参考我的另一个项目: 手写从零实现简易版 tomcat minicat 手写 nginx 系列 …...

leetcode290:单词规律
题目链接:290. 单词规律 - 力扣(LeetCode) class Solution { public:bool wordPattern(string pattern, string s) {unordered_map<char, string> s2t;unordered_map<string, char> t2s;int len pattern.size();int CountSpace…...

IDEA 2022
介绍 【尚硅谷IDEA安装idea实战教程(百万播放,新版来袭)】 jetbrains 中文官网 IDEA 官网 IDEA 从 IDEA 2022.1 版本开始支持 JDK 17,也就是说如果想要使用 JDK 17,那么就要下载 IDEA 2022.1 或之后的版本。 公司…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

企业大模型服务合规指南:深度解析备案与登记制度
伴随AI技术的爆炸式发展,尤其是大模型(LLM)在各行各业的深度应用和整合,企业利用AI技术提升效率、创新服务的步伐不断加快。无论是像DeepSeek这样的前沿技术提供者,还是积极拥抱AI转型的传统企业,在面向公众…...
之(六) ——通用对象池总结(核心))
怎么开发一个网络协议模块(C语言框架)之(六) ——通用对象池总结(核心)
+---------------------------+ | operEntryTbl[] | ← 操作对象池 (对象数组) +---------------------------+ | 0 | 1 | 2 | ... | N-1 | +---------------------------+↓ 初始化时全部加入 +------------------------+ +-------------------------+ | …...
