【数学】什么是傅里叶变换?什么是离散傅里叶变换?什么是拉普拉斯变换?
文章目录
- 什么是傅里叶变换?什么是离散傅里叶变换?什么是拉普拉斯变换?
- 背景
- 公式
- 示例题目
- 详细讲解
- Python代码求解
- 实际生活中的例子
- 什么是线性时不变系统
- 线性性(Linearity)
- 时不变性(Time-Invariance)
- LTI系统的分析方法
- 结论
什么是傅里叶变换?什么是离散傅里叶变换?什么是拉普拉斯变换?
背景
傅里叶变换、离散傅里叶变换和拉普拉斯变换都是在信号处理和系统分析中非常重要的工具。
- 傅里叶变换(Fourier Transform) 用于将时间或空间上的信号转换到频率域。通过傅里叶变换,我们可以分析信号的频率成分。
- 离散傅里叶变换(Discrete Fourier Transform, DFT) 是傅里叶变换在离散信号上的实现。它用于将有限长的序列转换到频率域。
- 拉普拉斯变换(Laplace Transform) 用于分析线性时不变系统。它将一个时间域的函数转换为复频域的函数,可以解决微分方程和控制系统问题。
公式
-
傅里叶变换
连续函数 f ( t ) f(t) f(t) 的傅里叶变换 F ( ω ) F(\omega) F(ω) 定义为:
F ( ω ) = ∫ − ∞ ∞ f ( t ) e − i ω t d t F(\omega) = \int_{-\infty}^{\infty} f(t) e^{-i \omega t} \, dt F(ω)=∫−∞∞f(t)e−iωtdt反傅里叶变换为:
f ( t ) = 1 2 π ∫ − ∞ ∞ F ( ω ) e i ω t d ω f(t) = \frac{1}{2\pi} \int_{-\infty}^{\infty} F(\omega) e^{i \omega t} \, d\omega f(t)=2π1∫−∞∞F(ω)eiωtdω -
离散傅里叶变换(DFT)
序列 x [ n ] x[n] x[n] 的离散傅里叶变换 X [ k ] X[k] X[k] 定义为:
X [ k ] = ∑ n = 0 N − 1 x [ n ] e − i 2 π N k n X[k] = \sum_{n=0}^{N-1} x[n] e^{-i \frac{2\pi}{N} kn} X[k]=n=0∑N−1x[n]e−iN2πkn反离散傅里叶变换为:
x [ n ] = 1 N ∑ k = 0 N − 1 X [ k ] e i 2 π N k n x[n] = \frac{1}{N} \sum_{k=0}^{N-1} X[k] e^{i \frac{2\pi}{N} kn} x[n]=N1k=0∑N−1X[k]eiN2πkn -
拉普拉斯变换
函数 f ( t ) f(t) f(t) 的拉普拉斯变换 F ( s ) F(s) F(s) 定义为:
F ( s ) = ∫ 0 ∞ f ( t ) e − s t d t F(s) = \int_{0}^{\infty} f(t) e^{-st} \, dt F(s)=∫0∞f(t)e−stdt其中, s s s 是复数,可以表示为 s = σ + i ω s = \sigma + i\omega s=σ+iω。
示例题目
-
傅里叶变换示例
求 f ( t ) = e − t u ( t ) f(t) = e^{-t} u(t) f(t)=e−tu(t) 的傅里叶变换,其中 u ( t ) u(t) u(t) 是单位阶跃函数。
-
离散傅里叶变换示例
对序列 x = [ 1 , 2 , 3 , 4 ] x = [1, 2, 3, 4] x=[1,2,3,4] 计算其离散傅里叶变换。
-
拉普拉斯变换示例
求 f ( t ) = e 3 t f(t) = e^{3t} f(t)=e3t 的拉普拉斯变换。
详细讲解
-
傅里叶变换示例讲解
对于 f ( t ) = e − t u ( t ) f(t) = e^{-t} u(t) f(t)=e−tu(t),傅里叶变换为:
F ( ω ) = ∫ 0 ∞ e − t e − i ω t d t = ∫ 0 ∞ e − ( 1 + i ω ) t d t F(\omega) = \int_{0}^{\infty} e^{-t} e^{-i \omega t} \, dt = \int_{0}^{\infty} e^{-(1 + i \omega)t} \, dt F(ω)=∫0∞e−te−iωtdt=∫0∞e−(1+iω)tdt这个积分是一个简单的指数积分,可以求得:
F ( ω ) = 1 1 + i ω F(\omega) = \frac{1}{1 + i \omega} F(ω)=1+iω1 -
离散傅里叶变换示例讲解
对于序列 x = [ 1 , 2 , 3 , 4 ] x = [1, 2, 3, 4] x=[1,2,3,4],计算其离散傅里叶变换:
X [ k ] = ∑ n = 0 3 x [ n ] e − i 2 π 4 k n X[k] = \sum_{n=0}^{3} x[n] e^{-i \frac{2\pi}{4} kn} X[k]=n=0∑3x[n]e−i42πkn具体计算为:
X [ 0 ] = 1 + 2 + 3 + 4 = 10 X[0] = 1 + 2 + 3 + 4 = 10 X[0]=1+2+3+4=10
X [ 1 ] = 1 + 2 e − i π 2 + 3 e − i π + 4 e − i 3 π 2 = 1 − 2 i − 3 + 4 i = − 2 + 2 i X[1] = 1 + 2e^{-i \frac{\pi}{2}} + 3e^{-i \pi} + 4e^{-i \frac{3\pi}{2}} = 1 - 2i - 3 + 4i = -2 + 2i X[1]=1+2e−i2π+3e−iπ+4e−i23π=1−2i−3+4i=−2+2i
X [ 2 ] = 1 + 2 e − i π + 3 e − i 2 π + 4 e − i 3 π = 1 − 2 + 3 − 4 = − 2 X[2] = 1 + 2e^{-i \pi} + 3e^{-i 2\pi} + 4e^{-i 3\pi} = 1 - 2 + 3 - 4 = -2 X[2]=1+2e−iπ+3e−i2π+4e−i3π=1−2+3−4=−2
X [ 3 ] = 1 + 2 e − i 3 π 2 + 3 e − i 3 π + 4 e − i 9 π 2 = 1 + 2 i − 3 − 4 i = − 2 − 2 i X[3] = 1 + 2e^{-i \frac{3\pi}{2}} + 3e^{-i 3\pi} + 4e^{-i \frac{9\pi}{2}} = 1 + 2i - 3 - 4i = -2 - 2i X[3]=1+2e−i23π+3e−i3π+4e−i29π=1+2i−3−4i=−2−2i -
拉普拉斯变换示例讲解
对于 f ( t ) = e 3 t f(t) = e^{3t} f(t)=e3t,拉普拉斯变换为:
F ( s ) = ∫ 0 ∞ e 3 t e − s t d t = ∫ 0 ∞ e ( 3 − s ) t d t F(s) = \int_{0}^{\infty} e^{3t} e^{-st} \, dt = \int_{0}^{\infty} e^{(3-s)t} \, dt F(s)=∫0∞e3te−stdt=∫0∞e(3−s)tdt这个积分是一个简单的指数积分,可以求得:
F ( s ) = 1 s − 3 对于 Re ( s ) > 3 F(s) = \frac{1}{s - 3} \quad \text{对于 } \text{Re}(s) > 3 F(s)=s−31对于 Re(s)>3
Python代码求解
import numpy as np# 离散傅里叶变换示例代码
x = np.array([1, 2, 3, 4])
X = np.fft.fft(x)
print("DFT of x:", X)
实际生活中的例子
- 傅里叶变换:在音频信号处理中,用于将声音分解成不同的频率分量。比如,用傅里叶变换来分析音乐中的不同音调和音符。
- 离散傅里叶变换:在图像处理中,用于图像的压缩和去噪。例如,JPEG图像压缩算法中使用了离散余弦变换(DCT),其原理类似于DFT。
- 拉普拉斯变换:在控制系统中,用于分析系统的稳定性和瞬态响应。例如,电路分析中的传递函数和机械系统的振动分析都使用拉普拉斯变换。
这些变换在工程和科学中的广泛应用,使得它们成为信号处理和系统分析中的基础工具。
什么是线性时不变系统
线性时不变系统(Linear Time-Invariant System,LTI系统)是控制理论和信号处理中的一个重要概念。它具有两个主要特性:线性性(Linearity)和时不变性(Time-Invariance)。理解这些特性有助于分析和设计许多实际系统。以下是对这两个特性的详细解释:
线性性(Linearity)
线性性包括两个方面:
-
齐次性(Homogeneity)或比例性(Scaling):
对于任意输入信号 ( x(t) ) 和常数 ( a ),系统的响应满足:
x ( t ) → y ( t ) ⟹ a ⋅ x ( t ) → a ⋅ y ( t ) x(t) \rightarrow y(t) \implies a \cdot x(t) \rightarrow a \cdot y(t) x(t)→y(t)⟹a⋅x(t)→a⋅y(t) -
可加性(Additivity)或叠加性(Superposition):
对于任意两个输入信号 ( x_1(t) ) 和 ( x_2(t) ),系统的响应满足:
x 1 ( t ) → y 1 ( t ) 和 x 2 ( t ) → y 2 ( t ) ⟹ x 1 ( t ) + x 2 ( t ) → y 1 ( t ) + y 2 ( t ) x_1(t) \rightarrow y_1(t) \quad \text{和} \quad x_2(t) \rightarrow y_2(t) \implies x_1(t) + x_2(t) \rightarrow y_1(t) + y_2(t) x1(t)→y1(t)和x2(t)→y2(t)⟹x1(t)+x2(t)→y1(t)+y2(t)
如果一个系统同时满足齐次性和可加性,那么它就是线性的。
时不变性(Time-Invariance)
时不变性意味着系统的特性不会随时间变化。也就是说,如果一个系统在时刻 ( t ) 的输入 ( x(t) ) 产生输出 ( y(t) ),那么对输入信号的任意时间平移 ( x(t - \tau) ) 产生的输出应为相同时间平移的输出信号 ( y(t - \tau) ):
x ( t ) → y ( t ) ⟹ x ( t − τ ) → y ( t − τ ) x(t) \rightarrow y(t) \implies x(t - \tau) \rightarrow y(t - \tau) x(t)→y(t)⟹x(t−τ)→y(t−τ)
LTI系统的分析方法
LTI系统的两个重要性质使得其分析和处理变得相对简单。以下是一些常用的方法:
-
脉冲响应(Impulse Response):
LTI系统可以通过其对单位脉冲信号 ( \delta(t) ) 的响应来完全描述。单位脉冲响应 ( h(t) ) 和任意输入 ( x(t) ) 的关系可以通过卷积积分表示:
y ( t ) = ( x ∗ h ) ( t ) = ∫ − ∞ ∞ x ( τ ) h ( t − τ ) d τ y(t) = (x * h)(t) = \int_{-\infty}^{\infty} x(\tau) h(t - \tau) d\tau y(t)=(x∗h)(t)=∫−∞∞x(τ)h(t−τ)dτ -
频率响应(Frequency Response):
LTI系统的频率响应可以通过其脉冲响应的傅里叶变换得到:
H ( ω ) = F { h ( t ) } H(\omega) = \mathcal{F}\{h(t)\} H(ω)=F{h(t)}
系统的输出信号的频谱是输入信号频谱和系统频率响应的乘积:
Y ( ω ) = X ( ω ) ⋅ H ( ω ) Y(\omega) = X(\omega) \cdot H(\omega) Y(ω)=X(ω)⋅H(ω) -
拉普拉斯变换(Laplace Transform):
对于连续时间系统,拉普拉斯变换可以用于求解系统的微分方程。系统的传递函数 ( H(s) ) 是脉冲响应的拉普拉斯变换:
H ( s ) = L { h ( t ) } H(s) = \mathcal{L}\{h(t)\} H(s)=L{h(t)}
输入输出关系可以表示为:
Y ( s ) = H ( s ) ⋅ X ( s ) Y(s) = H(s) \cdot X(s) Y(s)=H(s)⋅X(s) -
Z变换(Z-Transform):
对于离散时间系统,Z变换是类似的工具。系统的传递函数 ( H(z) ) 是脉冲响应的Z变换:
H ( z ) = Z { h [ n ] } H(z) = \mathcal{Z}\{h[n]\} H(z)=Z{h[n]}
输入输出关系可以表示为:
Y ( z ) = H ( z ) ⋅ X ( z ) Y(z) = H(z) \cdot X(z) Y(z)=H(z)⋅X(z)
结论
线性时不变系统(LTI系统)通过其线性性和时不变性特性,使得分析和设计变得较为简单。利用脉冲响应、频率响应、拉普拉斯变换和Z变换等工具,可以有效地处理和理解这些系统。
相关文章:

【数学】什么是傅里叶变换?什么是离散傅里叶变换?什么是拉普拉斯变换?
文章目录 什么是傅里叶变换?什么是离散傅里叶变换?什么是拉普拉斯变换?背景公式示例题目详细讲解Python代码求解实际生活中的例子 什么是线性时不变系统线性性(Linearity)时不变性(Time-Invariance…...
opencv安装笔记 各种平台
目录 python安装opencv-python c 麒麟arm系统安装和用法 python安装opencv-python pypi上搜索 Search results PyPI 现在安装是一个版本,大于3.6都可以安装 c 麒麟arm系统安装和用法 参考: ffmpeg rknn麒麟系统 安装 opencv_ffmpeg4 解码示例-CSDN…...

前端开发中的热更新原理
一、什么是热更新 热更新(Hot Module Replacement,HMR)是一种在前端开发中极为重要的技术。它允许开发者在不重新加载整个页面的情况下,实时更新应用程序中的某些模块。简单来说,热更新能让你在开发过程中即时看到代码…...

unix环境高级编程第2版:深入探索UNIX编程的奥秘
unix环境高级编程第2版:深入探索UNIX编程的奥秘 在数字世界的浩瀚海洋中,UNIX环境以其稳定、高效和灵活的特性,一直备受程序员们的青睐。而《unix环境高级编程第2版》这本书,无疑是探索UNIX编程奥秘的绝佳指南。接下来࿰…...
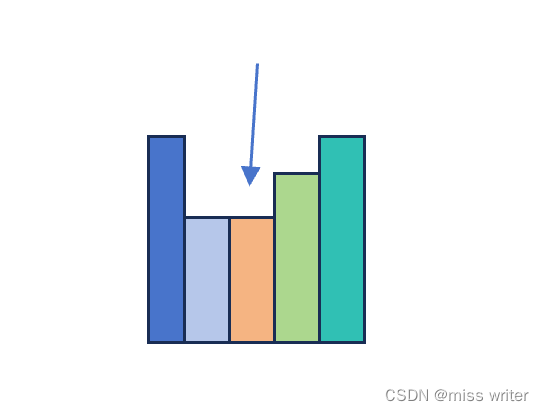
力扣42 接雨水
听说字节每人都会接雨水,我也要会哈哈哈 数据结构:数组 算法:核心是计算这一列接到多少雨水,它取决于它左边的最大值和右边的最大值,如下图第三根柱子能接到的雨水应该是第一根柱子高度和第五根柱子高度的最小值减去第…...

【代码随想录】【算法训练营】【第35天】[134]加油站 [135]分发糖果 [860]柠檬水找零 [406]根据身高重建队列
前言 思路及算法思维,指路 代码随想录。 题目来自 LeetCode。 day 35,连休两天~ 题目详情 [134] 加油站 题目描述 134 加油站 解题思路 前提:数组 思路:全局贪心算法:最小累加剩余汽油为负数,说明…...

Talk|新加坡国立大学贾鑫宇:适用于高自由度机器人的运动控制器
本期为TechBeat人工智能社区第600期线上Talk。 北京时间6月13日(周四)20:00,新加坡国立大学博士生—贾鑫宇的Talk已经准时在TechBeat人工智能社区开播! 他与大家分享的主题是: “适用于高自由度机器人的运动控制器”,向大家系统地介绍了如何通…...
【npm】console工具(含胶囊,表格,gif图片)
这是一款控制台花样输出工具 相对丰富的输出方式 文本输出属性值输出胶囊样式输出表格输出图片输出(含动图) 安装 npm install v_aot引用 import v_aot from "v_aot";字段说明 字段类型属性字符串值字符串类型default 、 primary 、 suc…...

OpenCV读取图片
import cv2 as cv # 读取图像 image cv.imread(F:\\mytupian\\xihuduanqiao.jpg) # 创建窗口 cv.namedWindow(image, cv.WINDOW_NORMAL) #显示图像后,允许用户随意调整窗口大小 # 显示图像 cv.imshow(image, image) cv.waitKey(0)import cv2 as cv srccv.imread(…...

HBase中的CRUD
Table接口:负责表数据的基本操作。 Admin类:负责管理建表、删表、该表等元数据操作的接口。 1、Put方法 1.1、了解put方法之前,必须知道的相关知识。 在HBase中有一个理念:所有的数据皆为bytes。因此在HBase中所有的数据最终都…...

C/C++学习笔记 C语言中的\0以及查找字符串中字符出现的频率
在此示例中,计算了字符串对象中字符的频率。 为此,使用size()函数查找字符串对象的长度。然后for 循环迭代直到字符串末尾。 在每次迭代中,检查字符是否出现,如果发现,则计数增加 1。 示例 1 #include <iostream&g…...

在C#中,有多种方式可以实现每天在指定的时间清空数据库数据。下面列出几种常用的方法,并提供简要的实现思路:
在C#中,实现每天在指定时间清空数据库数据的需求,可以通过多种方式来完成。下面列举了几种常用的方法: 方式一:使用 Task 和 Timer 这种方法利用 System.Threading.Timer 类来定时执行清空数据库的操作。 using System; using …...

深入理解java设计模式之单例模式
目录 概述单例模式是什么单例模式的使用场景单例模式的优缺点单例模式的几种实现方式饿汉式懒汉式双重检查锁定机制静态内部类枚举使用容器几种可能破坏单例类的方法多线程环境下的竞争条件使用反射机制使用序列化多个类加载器概述 单例模式是什么 定义:单例模式确保一个类在…...
程序员自由创业周记#36:Gap Year
程序员自由创业周记#36:Gap Year 一整年 刚过去的一周,度过了我31周岁的生日,距离结束上一份工作,刚好一年。一年过得好快,犹记得刚失业那会的迷茫,第一个月的纠结,是继续打工还是自己当“老板…...

Java 类与对象 -- Java 语言的类与对象、构造器、static、final、包和 JAR
大家好,我是栗筝i,这篇文章是我的 “栗筝i 的 Java 技术栈” 专栏的第 006 篇文章,在 “栗筝i 的 Java 技术栈” 这个专栏中我会持续为大家更新 Java 技术相关全套技术栈内容。专栏的主要目标是已经有一定 Java 开发经验,并希望进…...

MTK平台纯色背景抑制
MTK中有两个机制可以抑制纯色背景的亮度,分别是Main target、Histogram。 Main target的纯色背景亮度机制原理大概如下: 将图像分成64*48块,分别统计每一块的亮度Y。 但对于纯色背景时,如果仍然使用Luma来计算,容易造…...

Linux iptables使用详解
一、Linux系统下使用iptables 在Linux中,常用的防火墙工具是iptables。以下是一些基本的iptables命令,用于配置防火墙规则。 查看现有的iptables规则: sudo iptables -L 清除所有现有的规则(慎用,可能导致服务不可用…...
算法02 递归算法及其相关问题
递归 在编程中,我们把函数直接或者间接调用自身的过程叫做递归。 递归处理问题的过程是:通常把一个大型的复杂问题,转变成一个与原问题类似的,规模更小的问题来进行求解。 递归的三大要素 函数的参数。在用递归解决问题时&…...

三个pdf工具和浏览软件(pdftk,muppdf,epdfview)
安装pdftk pdftk是一款功能强大的PDF处理工具,主要用于对PDF文件进行各种操作。它提供了丰富的功能,包括但不限于合并、拆分、旋转、加密、解密、添加水印、从PDF文档中解出附件等。pdftk分为图形界面版本和命令行版本,适用于不同的用户需求…...
UKP3d的excel汇总表
长沙某正版用户就EXCEL的图框两点问题,进行交流: 1.1.图框:中英文两行,字体样式,logo加上等个性化需求; cbl回复:9.3后续版本迭代会加图框(解决用户个性化需求)…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...

BLEU评分:机器翻译质量评估的黄金标准
BLEU评分:机器翻译质量评估的黄金标准 1. 引言 在自然语言处理(NLP)领域,衡量一个机器翻译模型的性能至关重要。BLEU (Bilingual Evaluation Understudy) 作为一种自动化评估指标,自2002年由IBM的Kishore Papineni等人提出以来,…...

负载均衡器》》LVS、Nginx、HAproxy 区别
虚拟主机 先4,后7...

32位寻址与64位寻址
32位寻址与64位寻址 32位寻址是什么? 32位寻址是指计算机的CPU、内存或总线系统使用32位二进制数来标识和访问内存中的存储单元(地址),其核心含义与能力如下: 1. 核心定义 地址位宽:CPU或内存控制器用32位…...
