算法02 递归算法及其相关问题
递归
在编程中,我们把函数直接或者间接调用自身的过程叫做递归。
递归处理问题的过程是:通常把一个大型的复杂问题,转变成一个与原问题类似的,规模更小的问题来进行求解。
递归的三大要素
- 函数的参数。在用递归解决问题时,要合理地去设计函数的参数,达到当前问题与子问题之间的变化,可以通过参数进行准确地描述。
- 递推关系。要能够找到当前问题与子问题之间的联系,能够用子问题去描述当前问题的解。
- 递归出口(边界条件)。要找到问题的边界,避免出现无限递归的情况。每次我们在设计递归函数时,第一步就是先判断当前是否已经到达递归出口,若未到达则再继续递归。
偶数的递归定义
现在我们采用递归的方式来定义偶数:
- 0是一个偶数。
- 一个偶数与2的和是一个偶数。
这里我们在定义偶数时,就使用了偶数的这个概念。
证明10是偶数
现在我们需要使用刚才的定义来证明10是否为偶数。
因为10=8+2,根据第二条定义可以知道,一个偶数与2的和是一个偶数,现在我们只需要证明8是否是偶数即可得到结论。
我们现在用f(10)表示证明10是否为偶数的函数。
则整个的证明过程如下:
f(10) -> f(8) -> f(6) -> f(4) -> f(2) -> f(0),最终我们的问题变成证明0是否为偶数,而定义中已经给出0是偶数,所以我们可以得到2是偶数...依次类推。
f(0) -> f(2) -> f(4) -> f(6) -> f(8) -> f(10) 。
得出10是偶数。
参考代码
#include<bits/stdc++.h>
using namespace std;
bool f(int n){if(n==0)//如果n==0,则n是偶数return true;return f(n-2); //否则证明n-2是否为偶数
}
int main(){int n;cin>>n;cout<<f(n);return 0;
}输入奇数会怎么样?
输入奇数就会无限递归下去,因为我们并没有为n是奇数的情况设计递归出口。如果n=7,就会去求n=5、3、1、-1、-3...一直递归下去。
我们可以在函数中添加,针对奇数情况的递归出口。(当n==1时,返回false)
训练:递归求和
请使用递归的方法,计算1+2+3+...+n的和。
【输入描述】1行:输入一个整数n。
【输出描述】1行:输出一个整数,表示求和的结果。
【样例输入】5
【样例输出】15
参考代码
#include<bits/stdc++.h>
using namespace std;
int sum(int n){if(n==1)return 1;return sum(n-1)+n;
}
int main(){int n;cin>>n;cout<<sum(n);return 0;
}
训练:汉诺塔问题
汉诺塔(河内塔)问题是源于印度一个古老传说的益智玩具。大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定,在小圆盘上不能放大圆盘,在三根柱子之间一次只能移动一个圆盘。
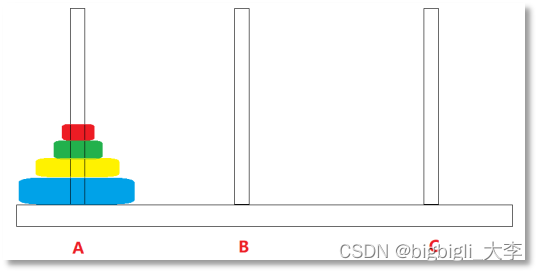
问题建模
我们可以使用4个参数去描述汉诺塔问题。
void Hanoi(int n,char a,char b,char c);
n表示移动的是第n号盘子;
a,b,c分别表示汉诺塔问题中的三个柱子。
我们称a,b,c分别为:起始柱,辅助柱,目标柱。
递归关系
- 根据游戏规则:想要移动n号盘,则需要先将n-1号盘从a柱移动到b柱。
此时我们的问题变成:Hanoi(n-1, a, c, b);
即:将n-1号盘从a柱出发,借助c柱,移动到b柱。
在这次移动的过程中a,c,b分别为:起始柱,辅助柱,目标柱。
- 将n-1号盘子移到b柱之后,我们就可以将n号盘子,直接从a移动到c,即:a->c。
到这一步,我们完成了第n号盘子的移动。
接下来我们还需要将n-1号盘子(在b柱),移动到c柱上。
即:Hanoi(n-1, b, a, c);
在这次移动的过程中b,a,c分别为:起始柱,辅助柱,目标柱。
边界条件
当问题变成只有一个盘子时,我们就无须借助辅助柱,
直接从a移动到c柱即可。
参考代码
void Hanoi(int n,char a,char b,char c){if(n==1){cout<<n<<":"<<a<<"->"<<c<<endl;return ;}else{Hanoi(n-1,a,c,b);cout<<n<<":"<<a<<"->"<<c<<endl;Hanoi(n-1,b,a,c);}
}
int main(){Hanoi(3,'a','b','c');return 0;
}从C++入门到算法,再到数据结构,查看全部文章请点击![]() http://www.bigbigli.com/
http://www.bigbigli.com/
相关文章:
算法02 递归算法及其相关问题
递归 在编程中,我们把函数直接或者间接调用自身的过程叫做递归。 递归处理问题的过程是:通常把一个大型的复杂问题,转变成一个与原问题类似的,规模更小的问题来进行求解。 递归的三大要素 函数的参数。在用递归解决问题时&…...

三个pdf工具和浏览软件(pdftk,muppdf,epdfview)
安装pdftk pdftk是一款功能强大的PDF处理工具,主要用于对PDF文件进行各种操作。它提供了丰富的功能,包括但不限于合并、拆分、旋转、加密、解密、添加水印、从PDF文档中解出附件等。pdftk分为图形界面版本和命令行版本,适用于不同的用户需求…...
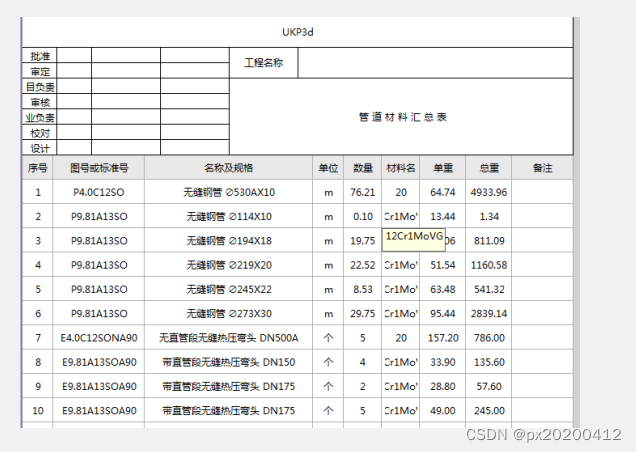
UKP3d的excel汇总表
长沙某正版用户就EXCEL的图框两点问题,进行交流: 1.1.图框:中英文两行,字体样式,logo加上等个性化需求; cbl回复:9.3后续版本迭代会加图框(解决用户个性化需求)…...

体验亚马逊AIGC——Amazon Bedrock
前言 随着人工智能技术的不断发展,我们已经进入了一个全新的时代,即AI驱动的时代。在这个时代,人工智能已经逐渐成为我们生活中不可或缺的一部分,它可以帮助我们更好地处理各种复杂的问题,提高我们的工作效率ÿ…...

Vue前端服务是什么:深入解析与实际应用
Vue前端服务是什么:深入解析与实际应用 在现今的互联网开发领域,前端技术日新月异,Vue.js作为其中的佼佼者,其前端服务更是成为了众多开发者关注的焦点。那么,Vue前端服务究竟是什么?它有哪些核心要素和实…...

mysql_ssl_rsa_setup使用详解
mysql_ssl_rsa_setup 是一个MySQL附带的工具,用于自动创建SSL证书和密钥文件,以便在MySQL服务器与客户端之间启用安全的SSL/TLS连接。这对于确保数据传输的安全性是非常重要的,尤其是在不安全的网络环境中。下面是对mysql_ssl_rsa_setup使用的…...
:FreeSWITCH基础概念与架构)
FreeSWITCH入门到精通系列(三):FreeSWITCH基础概念与架构
FreeSWITCH入门到精通系列(三):FreeSWITCH基础概念与架构 前言 在前两篇博客中,我们介绍了FreeSWITCH的基本概念和安装与配置。本篇文章将深入探讨FreeSWITCH的基础概念和架构,帮助您更好地理解这个强大的通信平台的…...
【C++】AVL树/红黑树实现及map与set的封装
前言 【C】二叉树进阶(二叉搜索树) 这篇文章讲述了关于二叉搜索树知识,但是二叉搜索树有其自身的缺陷,假如往树中插入的元素有序或者接近有序,二叉搜索树就会退化成单支树,时间复杂度会退化成O(N)ÿ…...

利用CSS隐藏HTML元素并插入替代内容
在创建一个支持切换阅读模式和答题模式的Anki问答题模板中,我创建了一个支持切换阅读模式和答题模式的问答题模板,该文最终利用JavaScript将Anki输出的向下箭头删除,并插入自定义的提示语。经过进一步测试,发现实现上述功能完全不…...

第二节 单机版本redis部署
1. 部署环境 操作系统:centos7.XCPU: 2H内存:4GIP: 192.168.100.102部署版本: redis-7.0.15.tar.gz基础环境: gcc下载 2. 上传Redis安装包 [rootlocalhost opt]# ll 总用量 2932 drwxrwxr-x. 8 root root 4096 1…...

Vim 常用指令
Vim 是一款功能强大且高度可定制的文本编辑器。其高效的编辑方式使其成为许多程序员和系统管理员的首选。 1. Vim 的基本模式 Vim 具有以下几种基本模式: 正常模式(Normal mode):用于浏览和编辑文本(按 ESC 进入&am…...

PySide6实现pdf转化为word和长图片
目录 一:实现思路 二:实现过程 三:完整代码和实现 一:实现思路 最近在使用wps,发现wps中使用pdf转化为长图片还需要收费,这么不地道。就想自己能不能用程序实现这种功能的。还好python在自动化办公领域比较强悍,对文档操作也是得心应手。因此记录下用python实现pdf转…...
嵌入式硬件VS软件,到底哪个更难?
在嵌入式系统开发中,硬件和软件是密不可分的两个方面。但是,究竟是硬件开发更具挑战性,还是软件开发更难以应对呢?本文将就这一问题展开讨论,探究嵌入式硬件和软件在开发过程中的各种挑战与特点。 一、硬件开发&#…...

Spring boot集成log4j及日志配置详解,实战,ELK使用教程。
目录 引言一、SpringBoot 集成 Log4j1. 添加 Log4j 依赖2. 移除默认的Logback组件3. 创建 Log4j 配置文件4. 配置 Log4j2 日志文件 二、Log4j2 XML 文件配置详解基本结构Appenders 配置详解Loggers 配置详解 三、日志的作用四、日志数据采集与分析1. 日志数据采集2. 日志数据分…...
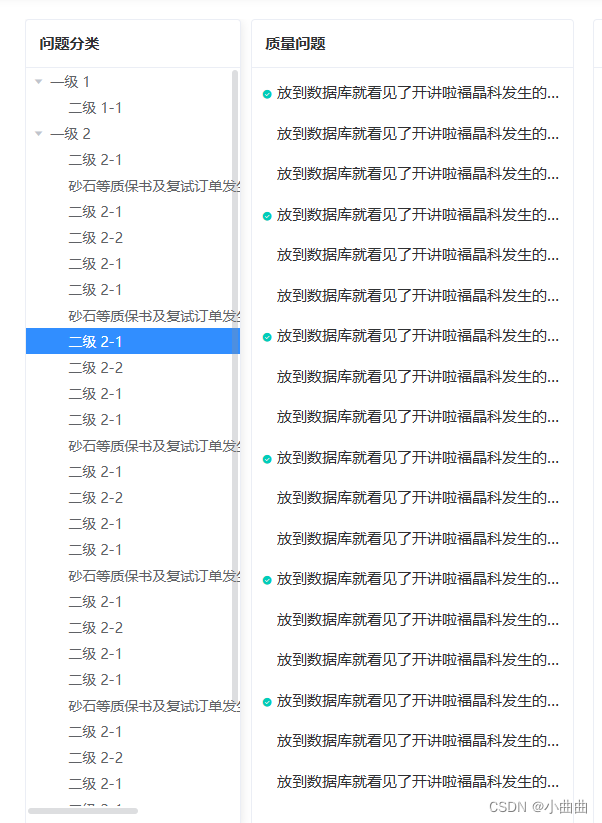
element 树组件 tree 横向纵向滚动条
Html <el-cardshadow"hover"class"solo flex-2"style"height: calc(100vh - 1.6rem); border: 1px solid #ebeef5"><div slot"header" class"clearfix"><span>问题分类</span></div><div …...

matlab 任意二维图像转点云
目录 一、概述二、代码实现三、结果展示本文由CSDN点云侠原创,原文链接。如果你不是在点云侠的博客中看到该文章,那么此处便是不要脸的爬虫。 一、概述 给定任意一张图片,通过代码操作将图片转成点云。图像中包含大量可用信息,其中必不可少的信息为像素坐标和像素值,将像…...

编程机器人的参数表怎么看
编程机器人的参数表怎么看 在探索编程机器人的世界时,理解其参数表是至关重要的一步。这些参数不仅反映了机器人的性能特点,还决定了其在实际应用中的表现。然而,对于初学者来说,参数表往往如同一本深奥的秘籍,充满了…...
上位机图像处理和嵌入式模块部署(h750 mcu串口命令处理)
【 声明:版权所有,欢迎转载,请勿用于商业用途。 联系信箱:feixiaoxing 163.com】 前面学习103和407的时候,当时学过串口的收发。不过当时使用的主要是阻塞的方式。这一次,我们看下应该怎么利用中断的形式进…...

西王食品2023营收下滑、净利润大幅减亏遭问询,近三年业绩承压
《港湾商业观察》廖紫雯 日前,西王食品股份有限公司(以下简称:西王食品,000639.SZ)收到来自深交所对公司2023年年报的问询函。 深交所问询函指出,要求公司说明营业收入下降、净利润大幅减亏的原因及合理性…...

视频媒介VS文字媒介
看到一篇蛮有思考意义的文章就摘录下来了,也引起了反思 目录 一、视频的定义 二、”视频媒介“与”文字媒介”作对比 1.形象 VS 抽象 2.被动 VS 主动 三、视频的缺点-【更少】的思考 1.看视频为啥会导致【更少的思考】 2.内容的【浅薄化】 3.内容的【娱乐化…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

pikachu靶场通关笔记19 SQL注入02-字符型注入(GET)
目录 一、SQL注入 二、字符型SQL注入 三、字符型注入与数字型注入 四、源码分析 五、渗透实战 1、渗透准备 2、SQL注入探测 (1)输入单引号 (2)万能注入语句 3、获取回显列orderby 4、获取数据库名database 5、获取表名…...

【C++】纯虚函数类外可以写实现吗?
1. 答案 先说答案,可以。 2.代码测试 .h头文件 #include <iostream> #include <string>// 抽象基类 class AbstractBase { public:AbstractBase() default;virtual ~AbstractBase() default; // 默认析构函数public:virtual int PureVirtualFunct…...
