在有向无环图(DAG)中实现拓扑排序与最短路径和最长路径算法
有向无环图(DAG)是一类非常重要的图结构,广泛应用于任务调度、数据依赖分析等领域。本文将介绍如何在DAG中实现拓扑排序、单源最短路径和单源最长路径算法,并提供完整的Java代码示例。
图结构定义
首先,我们定义一个简单的图结构,包括节点和边。使用Java代码如下:
import java.util.*;class Graph {final List<List<Edge>> adjList;public Graph(int vertices) {adjList = new ArrayList<>(vertices);for (int i = 0; i < vertices; i++) {adjList.add(new ArrayList<>());}}public void addEdge(int from, int to, int weight) {adjList.get(from).add(new Edge(from, to, weight));}public List<Edge> getEdges(int vertex) {return adjList.get(vertex);}public int size() {return adjList.size();}static class Edge {final int from;final int to;final int weight;Edge(int from, int to, int weight) {this.from = from;this.to = to;this.weight = weight;}@Overridepublic String toString() {return String.format("%d - %d: %d", from, to, weight);}}
}
拓扑排序算法
拓扑排序是DAG中非常基础且重要的算法。它为每个节点排列顺序,使得所有有向边从前往后指向。这里我们介绍两种拓扑排序算法:基于DFS和基于BFS的算法。
基于DFS的拓扑排序
import java.util.*;class TopologicalSort {public static List<Integer> sortDFS(Graph graph) {boolean[] visited = new boolean[graph.size()];Stack<Integer> stack = new Stack<>();for (int i = 0; i < graph.size(); i++) {if (!visited[i]) {topologicalSortUtil(graph, i, visited, stack);}}List<Integer> topoOrder = new ArrayList<>();while (!stack.isEmpty()) {topoOrder.add(stack.pop());}return topoOrder;}private static void topologicalSortUtil(Graph graph, int v, boolean[] visited, Stack<Integer> stack) {visited[v] = true;for (Graph.Edge edge : graph.getEdges(v)) {if (!visited[edge.to]) {topologicalSortUtil(graph, edge.to, visited, stack);}}stack.push(v);}
}
基于BFS的拓扑排序
import java.util.*;class TopologicalSort {public static List<Integer> sortBFS(Graph graph) {int[] inDegree = new int[graph.size()];for (List<Graph.Edge> edges : graph.adjList) {for (Graph.Edge edge : edges) {inDegree[edge.to]++;}}Queue<Integer> queue = new LinkedList<>();for (int i = 0; i < graph.size(); i++) {if (inDegree[i] == 0) {queue.offer(i);}}List<Integer> topoOrder = new ArrayList<>();while (!queue.isEmpty()) {int v = queue.poll();topoOrder.add(v);for (Graph.Edge edge : graph.getEdges(v)) {if (--inDegree[edge.to] == 0) {queue.offer(edge.to);}}}return topoOrder.size() == graph.size() ? topoOrder : new ArrayList<>(); // Check for cycle}
}
比较两种拓扑排序算法
-
DFS拓扑排序:
- 优点:实现简单,递归方式直观,适用于大部分编程场景。
- 缺点:需要使用额外的栈空间,可能导致栈溢出问题。
-
BFS拓扑排序(Kahn’s Algorithm):
- 优点:使用队列实现,避免了递归带来的栈空间问题。能有效检测图中的环。
- 缺点:实现稍微复杂,需要额外的入度数组。
基于拓扑排序的DAG单源最短路径算法
DAG中的单源最短路径算法可以利用拓扑排序来实现。由于DAG中不存在环,可以按照拓扑顺序依次松弛每个节点的边,从而实现单源最短路径。
import java.util.*;class ShortestPathDAG {public static int[] shortestPath(Graph graph, int start) {List<Integer> topoOrder = TopologicalSort.sortDFS(graph);int[] distTo = new int[graph.size()];Arrays.fill(distTo, Integer.MAX_VALUE);distTo[start] = 0;for (int v : topoOrder) {if (distTo[v] != Integer.MAX_VALUE) {for (Graph.Edge edge : graph.getEdges(v)) {if (distTo[v] + edge.weight < distTo[edge.to]) {distTo[edge.to] = distTo[v] + edge.weight;}}}}return distTo;}
}
最短路径算法与Dijkstra算法的优劣性比较
-
优点:
- 拓扑排序+最短路径算法在DAG中效率高,可以在线性时间内解决最短路径问题。
- 对于DAG来说,算法实现相对简单。
-
缺点:
- 仅适用于DAG,对于有环图无效。
- Dijkstra算法适用于任意有向图和无向图,且能处理正权边的最短路径问题。
基于拓扑排序的DAG单源最长路径算法
方法1:使用图的副本和最短路径算法
import java.util.*;class LongestPathDAG {public static int[] longestPathWithNegation(Graph graph, int start) {Graph negatedGraph = new Graph(graph.size());for (int i = 0; i < graph.size(); i++) {for (Graph.Edge edge : graph.getEdges(i)) {negatedGraph.addEdge(edge.from, edge.to, -edge.weight);}}int[] negatedDistances = ShortestPathDAG.shortestPath(negatedGraph, start);int[] distances = new int[graph.size()];for (int i = 0; i < negatedDistances.length; i++) {distances[i] = -negatedDistances[i];}return distances;}
}
方法2:直接修改最短路径算法
import java.util.*;class LongestPathDAG {public static int[] longestPathDirect(Graph graph, int start) {List<Integer> topoOrder = TopologicalSort.sortDFS(graph);int[] distTo = new int[graph.size()];Arrays.fill(distTo, Integer.MIN_VALUE);distTo[start] = 0;for (int v : topoOrder) {if (distTo[v] != Integer.MIN_VALUE) {for (Graph.Edge edge : graph.getEdges(v)) {if (distTo[v] + edge.weight > distTo[edge.to]) {distTo[edge.to] = distTo[v] + edge.weight;}}}}return distTo;}
}
比较两种单源最长路径算法
-
使用图的副本和最短路径算法:
- 优点:利用现有的最短路径算法作为黑箱,方便直接调用。
- 缺点:需要额外创建图的副本,增加了时间和空间复杂度。
-
直接修改最短路径算法:
- 优点:无需额外的图副本,算法效率更高,直接适用于最长路径问题。
- 缺点:实现稍微复杂,需要对算法进行适当调整。
主类(用于测试)
public class Main {public static void main(String[] args) {Graph graph = new Graph(6);graph.addEdge(0, 1, 5);graph.addEdge(0, 2, 3);graph.addEdge(1, 3, 6);graph.addEdge(1, 2, 2);graph.addEdge(2, 4, 4);graph.addEdge(2, 5, 2);graph.addEdge(2, 3, 7);graph.addEdge(3, 4, -1);graph.addEdge(3, 5, 1);graph.addEdge(4, 5, -2);List<Integer> topoOrderDFS = TopologicalSort.sortDFS(graph);System.out.println("Topological Sort (DFS): " + topoOrderDFS);List<Integer> topoOrderBFS = TopologicalSort.sortBFS(graph);System.out.println("Topological Sort (BFS): " + topoOrderBFS);int[] shortestPaths = ShortestPathDAG.shortestPath(graph, 0);System.out.println("Shortest Paths from vertex 0: " + Arrays.toString(shortestPaths));int[] longestPathsNegation = LongestPathDAG.longestPathWithNegation(graph, 0);System.out.println("Longest Paths from vertex 0 (with negation): " + Arrays.toString(longestPathsNegation));int[] longestPathsDirect = LongestPathDAG.longestPathDirect(graph, 0);System.out.println("Longest Paths from vertex 0 (direct method): " + Arrays.toString(longestPathsDirect));}
}
总结
本文介绍了在有向无环图(DAG)中实现拓扑排序、单源最短路径和单源最长路径算法的详细步骤和Java代码。通过比较不同的拓扑排序方法和最长路径算法,我们可以根据实际需求选择最适合的实现方案。希望这些内容能帮助读者更好地理解和应用DAG相关的算法。
相关文章:
中实现拓扑排序与最短路径和最长路径算法)
在有向无环图(DAG)中实现拓扑排序与最短路径和最长路径算法
有向无环图(DAG)是一类非常重要的图结构,广泛应用于任务调度、数据依赖分析等领域。本文将介绍如何在DAG中实现拓扑排序、单源最短路径和单源最长路径算法,并提供完整的Java代码示例。 图结构定义 首先,我们定义一个…...

SQLServer按照年龄段进行分组查询数据
1.按照年龄段对数据进行分组, 将人群分为:青年,中年,老年三种类型,人群类型加上其他分组字段如:性别,进行多条件分组,统计各个年龄段多少人 Select case sex when 1 then ‘男’ when 2 then …...

开放式耳机哪个品牌质量比较好?2024高性价比机型推荐!
随着音乐技术的不断发展,开放式耳机已成为音乐发烧友们的另外一种选择。从最初的简单音质,到如今的高清解析,开放式耳机不断进化升级。音质纯净,佩戴舒适,无论是街头漫步还是家中放松时候,都能带给你身临其…...

Blender骨骼创建
骨骼系统 建立 使用Shift A添加骨骼或在添加|骨架中添加一段骨骼 骨骼的三种模式 -物体模式:做动画,摆人物pose时在该模式 -编辑模式:进行骨骼搭建(选择一段骨骼,然后按E挤出一段骨骼并进行调整) -姿…...
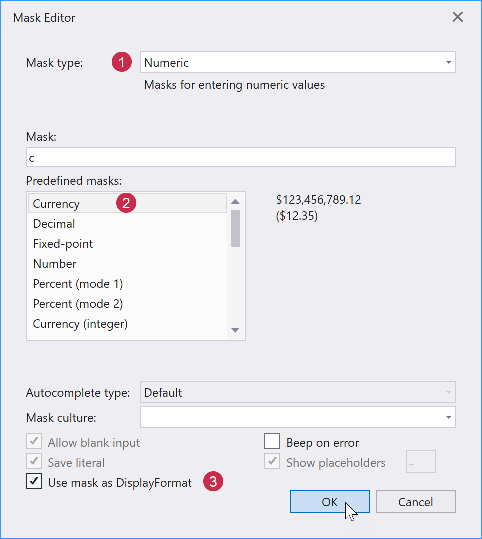
DevExpress WPF中文教程:Grid - 如何完成列和编辑器配置(设计时)?
DevExpress WPF拥有120个控件和库,将帮助您交付满足甚至超出企业需求的高性能业务应用程序。通过DevExpress WPF能创建有着强大互动功能的XAML基础应用程序,这些应用程序专注于当代客户的需求和构建未来新一代支持触摸的解决方案。 无论是Office办公软件…...

高考完的三个月想自学点编程,有没有什么建议
👆点击关注 获取更多编程干货👆 对于刚刚完成高考的学生来说,无论未来是否选择计算机科学作为专业方向,自学编程技能是一项非常有价值的投资,掌握编程知识能够帮助同学们为将来的学习和科研 实践奠定一个基础。 随着…...

运维开发(DevOps):加速软件交付的关键方法
1. 什么是运维开发 运维开发(DevOps)是将软件开发(Development)与信息技术运维(Operations)的流程整合在一起的实践方法。DevOps的目标是通过增强开发和运维团队之间的协作,提高软件产品的发布…...

Vue前端环境搭建:从四个方面、五个方面、六个方面和七个方面深度解析
Vue前端环境搭建:从四个方面、五个方面、六个方面和七个方面深度解析 在构建Vue.js项目时,搭建一个稳定且高效的前端环境至关重要。这不仅关乎项目的顺利推进,更直接影响开发者的效率和代码质量。本文将从四个方面、五个方面、六个方面和七个…...

农业领域科技查新点提炼方法附案例!
农业学科是人类通过改造和利用生物有机体(植物、动物、微生物等)及各种自然资源(光、热、水、土壤等)生产出人类需求的农产品的过程,人类在这一过程中所积累的科学原理、技术、工艺和技能,统称为农业科学技术,该领域具有研究范围广、综合性强…...
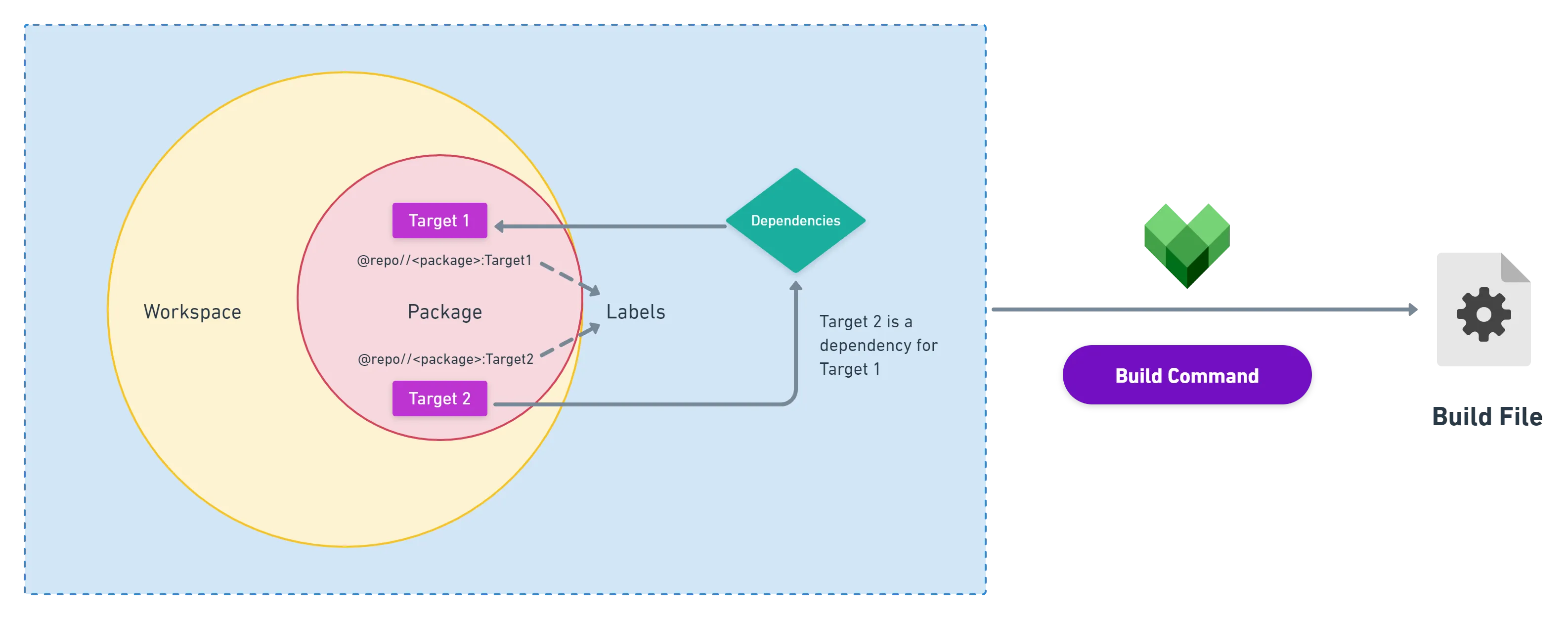
【Bazel入门与精通】 rules之属性
https://bazel.build/extending/rules?hlzh-cn#attributes Attributes An attribute is a rule argument. Attributes can provide specific values to a target’s implementation, or they can refer to other targets, creating a graph of dependencies. Rule-specifi…...
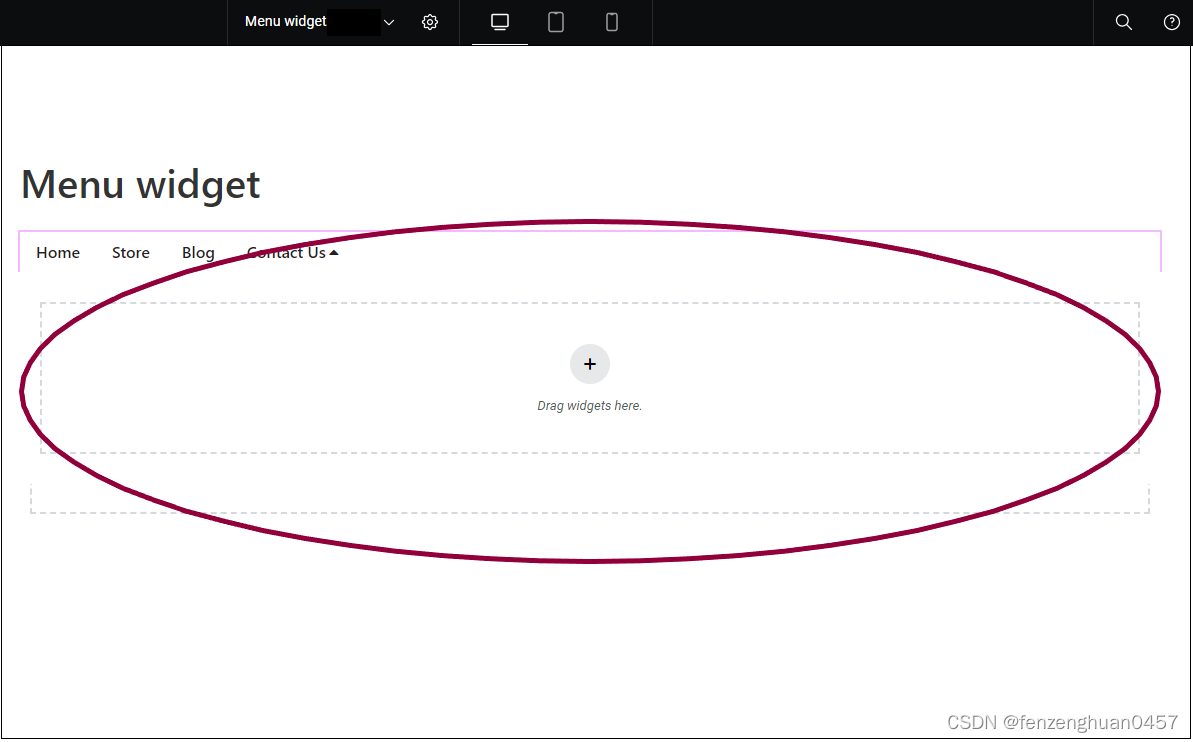
Elementor无需第三方插件实现高级下拉菜单/巨型菜单
使用新的嵌套功能创建美观的菜单和大型菜单。巨型菜单是具有复杂导航结构和独特设计的网站的理想选择。 Elementor-设置-特性-Menu启用 之后再去前端编辑器设计即可,就会有一个新的menu菜单模块了。 这个菜单的下拉则是通过Elementor直接来设计,也就以为…...

【数学】什么是傅里叶变换?什么是离散傅里叶变换?什么是拉普拉斯变换?
文章目录 什么是傅里叶变换?什么是离散傅里叶变换?什么是拉普拉斯变换?背景公式示例题目详细讲解Python代码求解实际生活中的例子 什么是线性时不变系统线性性(Linearity)时不变性(Time-Invariance…...
opencv安装笔记 各种平台
目录 python安装opencv-python c 麒麟arm系统安装和用法 python安装opencv-python pypi上搜索 Search results PyPI 现在安装是一个版本,大于3.6都可以安装 c 麒麟arm系统安装和用法 参考: ffmpeg rknn麒麟系统 安装 opencv_ffmpeg4 解码示例-CSDN…...

前端开发中的热更新原理
一、什么是热更新 热更新(Hot Module Replacement,HMR)是一种在前端开发中极为重要的技术。它允许开发者在不重新加载整个页面的情况下,实时更新应用程序中的某些模块。简单来说,热更新能让你在开发过程中即时看到代码…...

unix环境高级编程第2版:深入探索UNIX编程的奥秘
unix环境高级编程第2版:深入探索UNIX编程的奥秘 在数字世界的浩瀚海洋中,UNIX环境以其稳定、高效和灵活的特性,一直备受程序员们的青睐。而《unix环境高级编程第2版》这本书,无疑是探索UNIX编程奥秘的绝佳指南。接下来࿰…...
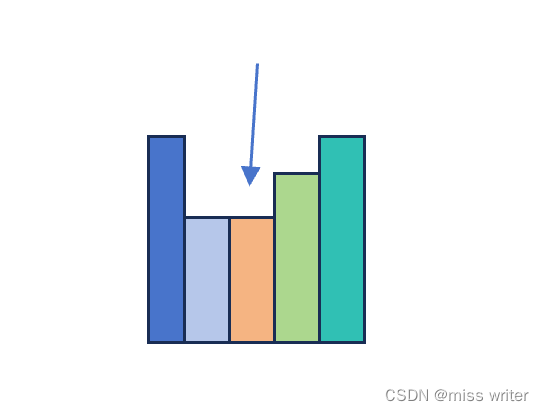
力扣42 接雨水
听说字节每人都会接雨水,我也要会哈哈哈 数据结构:数组 算法:核心是计算这一列接到多少雨水,它取决于它左边的最大值和右边的最大值,如下图第三根柱子能接到的雨水应该是第一根柱子高度和第五根柱子高度的最小值减去第…...

【代码随想录】【算法训练营】【第35天】[134]加油站 [135]分发糖果 [860]柠檬水找零 [406]根据身高重建队列
前言 思路及算法思维,指路 代码随想录。 题目来自 LeetCode。 day 35,连休两天~ 题目详情 [134] 加油站 题目描述 134 加油站 解题思路 前提:数组 思路:全局贪心算法:最小累加剩余汽油为负数,说明…...

Talk|新加坡国立大学贾鑫宇:适用于高自由度机器人的运动控制器
本期为TechBeat人工智能社区第600期线上Talk。 北京时间6月13日(周四)20:00,新加坡国立大学博士生—贾鑫宇的Talk已经准时在TechBeat人工智能社区开播! 他与大家分享的主题是: “适用于高自由度机器人的运动控制器”,向大家系统地介绍了如何通…...
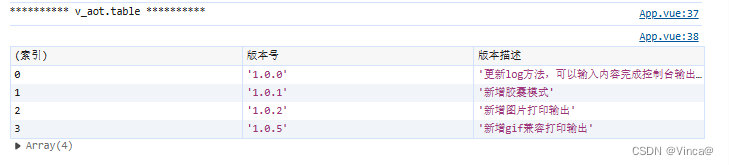
【npm】console工具(含胶囊,表格,gif图片)
这是一款控制台花样输出工具 相对丰富的输出方式 文本输出属性值输出胶囊样式输出表格输出图片输出(含动图) 安装 npm install v_aot引用 import v_aot from "v_aot";字段说明 字段类型属性字符串值字符串类型default 、 primary 、 suc…...

OpenCV读取图片
import cv2 as cv # 读取图像 image cv.imread(F:\\mytupian\\xihuduanqiao.jpg) # 创建窗口 cv.namedWindow(image, cv.WINDOW_NORMAL) #显示图像后,允许用户随意调整窗口大小 # 显示图像 cv.imshow(image, image) cv.waitKey(0)import cv2 as cv srccv.imread(…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...
