r语言数据分析案例25-基于向量自回归模型的标准普尔 500 指数长期预测与机制分析
一、背景介绍
2007 年的全球经济危机深刻改变了世界经济格局,引发了一系列连锁反应,波及各大洲。经济增长停滞不前,甚至在某些情况下出现负增长,给出口导向型发展中国家带来了不确定性。实体经济受到的冲击尤为严重,生产成本上升,利润下降,实际经济价值缩水。相比之下,金融部门的投资活动激增,原因是在动荡的经济环境中寻求稳定和更高的回报。然而,金融投资的性质与实体经济有很大不同,实体经济的特点是复杂且往往不可预测的因素交织在一起。。。。。
二、研究现状
理解和掌握标准普尔 500 指数的变化规律,对于正确评估美国经济趋势、跟踪世界经济发展的源和流、参与全球市场套利和定价具有重要的现实意义。基于标准普尔 500 指数在金融市场中的重要地位,标准普尔 500 指数的预测受到研究人员的更多关注。
目前对标准普尔 500 指数的研究主要集中在短期预测上,使用不同的研究工具。例如,[1]在预测标准普尔 500 指数值时使用隐马尔可夫链方法和离散时间马尔可夫链方法,指出使用全样本数据和特征子样本时预测效果更好。。。。。。
三、数据集介绍和分析
3.1 数据分析
在这项研究中,选择了美国股票的标准普尔 500 指数进行预测分析,并初步选择开盘价、最高价、最低价和收盘价作为研究数据。
标准普尔 500 指数的数据收集时间为 1995 年 1 月 3 日至 2020 年 12 月 31 日,包括该期间内的交易日。
代码和数据
报告代码和数据
library(quantmod)
library(TTR)data$Date <- as.Date(data$Date, format = "%Y/%m/%d")# (VWAP)
data$VWAP <- with(data, rowSums(data[, c("High", "Low", "Close")]) / 3 * Volume / sum(data$Volume))#### Convert data to xts objects
HTM_xts <- xts(HTM[, c("Open", "High", "Low", "Close")], order.by = HTM$Date)plot(HTM_xts)
addLegend("topleft", legend.names = colnames(HTM_xts), lwd = 1)
3.2稳定性分析
该检验的原假设和备择假设为:
原假设:该序列存在单位根。
备择假设:该序列不存在单位根。
如果我们不能拒绝原假设,我们可以说该序列是非平稳的。

以收盘价为例,通过上图我们可以看出,该指数的均值和标准差都在增加,初步判断该序列是非平稳的。
表 1. 单位根检验的结果
| Variable | ADF Statistic | p value | |
| Dickey-Fuller Test | Open | -0.428 | 0.985 |
| High | -0.250 | 0.990 | |
| Low | -0.525 | 0.981 | |
| Close | -0.442 | 0.984 |
从表 1 中,我们观察到所有四个时间序列的 p 值都大于 0.05。因此,我们不能拒绝原假设,并得出时间序列是非平稳的结论。为了解决这个问题,我们需要对序列进行差分。

| Variable | ADF Statistic | p value | |
| Dickey-Fuller Test | Open | -18.943 | 0.010 |
| High | -18.834 | 0.010 | |
| Low | -18.697 | 0.010 | |
| Close | -18.742 | 0.010 |
四、方法理论
向量自回归(VAR)模型是自回归(AR)模型的扩展,是一种常用的计量经济模型[6]。它考虑了多个变量之间的相互依赖关系,比简单的 AR 模型更全面。。。。。
五、模型建立和分析
选择 1995-01-03 至 2020-11-16 期间作为训练集,预测 2020-11-17 至 2020-12-31 期间的数据。
| AIC(n) | HQ(n) | SC(n) | FPE(n) | |
| 1 | 17.678 | 17.686 | 17.699 | 47606900.000 |
| 2 | 17.073 | 17.086 | 17.111 | 25986330.000 |
| 3 | 16.810 | 16.829 | 16.865 | 19983500.000 |
| 4 | 16.735 | 16.759 | 16.805 | 18523240.000 |
| 5 | 16.583 | 16.613 | 16.670 | 15910690.000 |
| 6 | 16.513 | 16.549 | 16.617 | 14837310.000 |
| 7 | 16.442 | 16.484 | 16.563 | 13826240.000 |
| 8 | 16.391 | 16.439 | 16.529 | 13139830.000 |
| 9 | 16.307 | 16.360 | 16.461 | 12075260.000 |
| 10 | 16.273 | 16.332 | 16.444 | 11673230.000 |
我们可以看到,不同的标准选择了相同的滞后长度(n=10)。当滞后长度超过 3 时,AIC 值的下降幅度变小,这表明在 3 之后添加更多的滞后观测值并不会显著提高模型拟合度。因此,按照选择 AIC 值较小的更简单模型的原则,我们选择 p=3 作为滞后阶数。
| Estimation results for equation Open: | ||||
| Open = Open.l1 + High.l1 + Low.l1 + Close.l1 + Open.l2 + High.l2 + Low.l2 + Close.l2 + Open.l3 + High.l3 + Low.l3 + Close.l3 + const | ||||
| Estimate | Std.Error | t value | Pr(>|t|) | |
| Open.l1 | -0.840 | 0.018 | -45.764 | < 2e-16 *** |
| High.l1 | -0.004 | 0.016 | -0.229 | 0.819 |
| Low.l1 | 0.043 | 0.014 | 3.079 | 0.00209 ** |
| Close.l1 | 0.897 | 0.012 | 72.094 | < 2e-16 *** |
| Open.l2 | -0.309 | 0.020 | -15.594 | < 2e-16 *** |
| High.l2 | -0.113 | 0.019 | -6.031 | 1.72e-09 *** |
| Low.l2 | 0.001 | 0.016 | 0.072 | 0.943 |
| Close.l2 | 0.820 | 0.018 | 44.881 | < 2e-16 *** |
| Open.l3 | -0.011 | 0.013 | -0.852 | 0.395 |
| High.l3 | -0.108 | 0.016 | -6.676 | 2.66e-11 *** |
| Low.l3 | -0.017 | 0.014 | -1.200 | 0.230 |
| Close.l3 | 0.367 | 0.016 | 22.711 | < 2e-16 *** |
| const | 0.135 | 0.093 | 1.449 | 0.147 |
| Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 | ||||
| Residual standard error: 7.522 on 6499 degrees of freedom | ||||
| Multiple R-Squared: 0.8063, Adjusted R-squared: 0.8059 | ||||
| F-statistic: 2254 on 12 and 6499 DF, p-value: < 2.2e-16 | ||||
| Estimation results for equation High: | ||||
| High = Open.l1 + High.l1 + Low.l1 + Close.l1 + Open.l2 + High.l2 + Low.l2 + Close.l2 + Open.l3 + High.l3 + Low.l3 + Close.l3 + const | ||||
| Estimate | Std.Error | t value | Pr(>|t|) | |
| Open.l1 | -0.196 | 0.030 | -6.592 | 4.69e-11 *** |
| High.l1 | -0.680 | 0.026 | -25.885 | < 2e-16 *** |
| Low.l1 | 0.041 | 0.023 | 1.815 | 0.06952 . |
| Close.l1 | 0.698 | 0.020 | 34.741 | < 2e-16 *** |
| Open.l2 | 0.133 | 0.032 | 4.164 | 3.16e-05 *** |
| High.l2 | -0.538 | 0.030 | -17.707 | < 2e-16 *** |
| Low.l2 | -0.018 | 0.026 | -0.714 | 0.475 |
| Close.l2 | 0.715 | 0.030 | 24.222 | < 2e-16 *** |
| Open.l3 | 0.111 | 0.021 | 5.308 | 1.14e-07 *** |
| High.l3 | -0.324 | 0.026 | -12.385 | < 2e-16 *** |
| Low.l3 | -0.015 | 0.022 | -0.658 | 0.511 |
| Close.l3 | 0.281 | 0.026 | 10.743 | < 2e-16 *** |
| const | 0.391 | 0.151 | 2.592 | 0.00955 ** |
| Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 | ||||
| Residual standard error: 12.15 on 6499 degrees of freedom | ||||
| Multiple R-Squared: 0.3167, Adjusted R-squared: 0.3154 | ||||
| F-statistic: 251 on 12 and 6499 DF, p-value: < 2.2e-16 | ||||
模型检验
为了确保模型已经捕获了数据中的所有方差和模式,我们需要测试残差项中是否存在剩余相关性。
| Portmanteau Test (asymptotic) | ||
| Chi-squared = 850.9 | df = 0 | p-value < 2.2e-16 |
非常小的 p 值表明拒绝了无自相关的原假设。这是一个信号,表明需要增加滞后长度。我们可以考虑在 VAR 模型中选择更高的滞后阶数,以使残差中的自相关在很大程度上被消除。以“Close”为例,可以看出模型的预测性能不是很令人满意(见图 5)。

comparison_df <- data.frame(date = forecast_df$date,forecasted = forecast_df$close,actual = test_o$Close
)
comparison_dfggplot(comparison_df, aes(x = date)) +geom_line(aes(y = forecasted, color = "Forecasted")) +geom_line(aes(y = Close, color = "Actual")) +labs(x = "Date", y = "Close Value", color = "Data") +scale_color_manual(values = c("Forecasted" = "blue", "Actual" = "red")) +theme_minimal()+theme(panel.border = element_rect(color = "black", fill = NA), panel.grid.major = element_blank(), panel.grid.minor = element_blank())
四个指数的预测误差在 50 左右。
| Open | High | Low | Close | |
| RMSE | 54.559 | 54.141 | 57.482 | 58.794 |
可视化结果如下
###plot
rmse_open <- 54.55896
rmse_high <- 54.14115
rmse_low <- 57.48235
rmse_close <- 58.79398rmse_data <- data.frame(RMSE = c(rmse_open, rmse_high, rmse_low, rmse_close),Type = c("Open", "High", "Low", "Close")
)barplot(rmse_data$RMSE, names.arg = rmse_data$Type, main = "RMSE Values",xlab = "Type",ylab = "RMSE",col = rainbow(length(rmse_data$RMSE))) text(x = 1:length(rmse_data$RMSE), y = rmse_data$RMSE, label = round(rmse_data$RMSE, 2), pos = 3, cex = 0.8, col = "black",xpd = TRUE) 
接下来,使用欧美汇率数据对 S&P 500 股票价格和其他特征进行多元线性回归: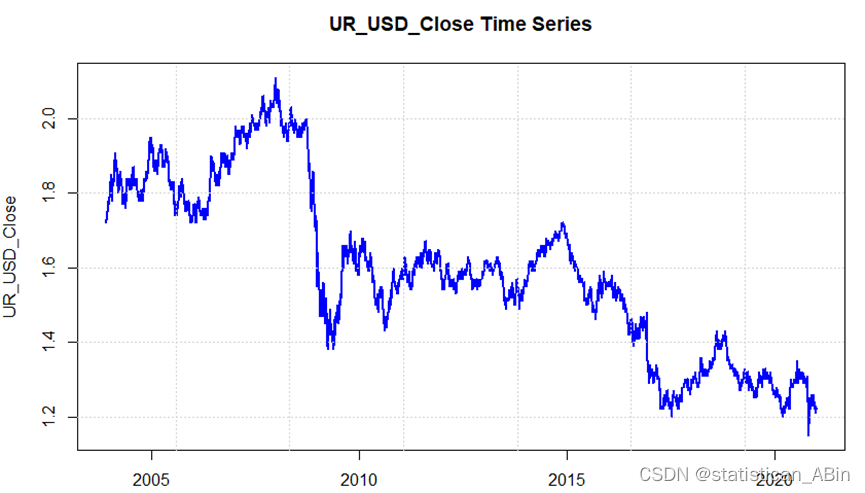
| Call: | ||||
| lm(formula = dataset$UR_USD Close ~ log_Open + log_High + log_Low + log_Close, data = dataset) | ||||
| Residuals: | ||||
| Min | 1Q | Median | 3Q | Max |
| -0.48796 | -0.09936 | -0.02465 | 0.08142 | 0.48518 |
| Coefficients: | ||||
| Estimate | Std. Error | t value | Pr(>|t|) | |
| (Intercept) | 4.80613 | 0.05312 | 90.480 | < 0.0000 *** |
| log_Open | 0.51837 | 0.61270 | 0.846 | 0.397575 |
| log_High | -2.27459 | 0.66081 | -3.442 | 0.0006 *** |
| log_Low | 1.98556 | 0.56573 | 3.510 | 0.000453 *** |
| log_Close | -0.65925 | 0.59302 | -1.112 | 0.266336 |
| Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 | ||||
| Residual standard error: 0.1658 on 4297 degrees of freedom Multiple R-squared: 0.4693, Adjusted R-squared: 0.4689 F-statistic: 950.1 on 4 and 4297 DF, p-value: < 0.00000000000000022 | ||||
从上述模型拟合结果可以看出,去除对数后的每日最高价和每日最低价是最显著的水平,因此从理论上讲,它们对欧美汇率有影响。
六、结论
在这项研究中,VAR 模型被用于对标准普尔 500 指数的开盘价、最高价、最低价和收盘价进行多变量预测。然而,我们的分析表明,虽然 VAR 模型在捕捉一些变量之间的线性关系方面表现良好,但它可能无法完全捕捉非线性驱动因素的影响。随后,我们使用欧美汇率数据,结合标准普尔 500 股票和其他特征的数据,对数据进行多元线性回归和对数处理,最终结果表明,标准普尔 500 指数的每日最高价和最低价对欧元兑美元汇率有显著影响。
在未来的实验过程中,可以选择特征进行进一步的影响分析,如脉冲响应和方差分解等,这些可以继续探索影响因素,同时为经济投资提供一定程度的指导。
七、参考文献
[1]Hashemi, Ray R., et al. Extraction of the Essential Constituents of the S&P 500 Index. 2017 international conference on computational science and computational intelligence (CSCI). IEEE, 2017.
[2]Sukparungsee, S. . A comparison of s&p 500 index forecasting models of arima, arima with garch-m and arima with e-garch.International Journal of Technical Research and Applications,32,2015.
[3]K.J.M. Cremers. Stock return predictability. a Bayesian model selection perspective. Rev. Financ. Stud,15(4), 1223–1249,2002.
[4]Wang F .Predicting S&P 500 Market Price by Deep Neural Network and Enemble Model[J].E3S Web of Conferences, 2020.DOI:10.1051/e3sconf/202021402040.
[5]G. M. Siddesh,et al.A Long Short-Term Memory Network-Based Approach for Predicting the Trends in the S&P 500 Index.Journal of The Institution of Engineers.1(105),19-26,2024.
数据和代码
代码和完整报告
创作不易,希望大家多多点赞收藏和评论!
相关文章:

r语言数据分析案例25-基于向量自回归模型的标准普尔 500 指数长期预测与机制分析
一、背景介绍 2007 年的全球经济危机深刻改变了世界经济格局,引发了一系列连锁反应,波及各大洲。经济增长停滞不前,甚至在某些情况下出现负增长,给出口导向型发展中国家带来了不确定性。实体经济受到的冲击尤为严重,生…...
解决使用Jmeter进行测试时出现“302“,‘‘401“等用户未登录的问题
使用 JMeter 压力测试时解决登录问题的两种方法 在使用 JMeter 进行压力测试时,可能会遇程序存在安全验证,必须登录后才能对里面的具体方法进行测试: 如果遇到登录问题,通常是因为 JMeter 无法模拟用户的登录状态,导…...

MySql通过 Procedure 循环删除数据
一、问题描述 在日常使用运维中,一些特殊情况需要批量删除陈旧或异常数据。 如果通过 delete from 【表名】 where 【条件】 直接删除,可能会由于数据量过大,事务执行时间过长,造成死锁。 二、解决方案 通过 Procedure 使用循环…...

Spring Boot 的启动原理、Spring Boot 自动配置原理
Spring Boot启动原理包含自动装配原理。 Spring Boot 的启动原理: 1. 入口类与 SpringApplication 初始化: 应用程序通常从一个带有 SpringBootApplication 注解的主类开始,这个注解是一个组合注解,包含了 SpringBootConfigurat…...

不会开发的你也能管理好企业漏洞,开源免费工具:洞察(insight II)
公司刚开始建设安全管理时,都是从一片混沌开始的,资源总是不够的,我们每个做安全的人员,又要会渗透,又要抓制度,还得管理各种漏洞。在管理楼栋是,我相信大家都遇到过以下几个问题: …...

java实现两个不同对象的集合复制
场景: 我们开发中会遇到集合对象复制的场景,可以避免代码的重复编写 基于 com.alibaba.fastjson.JSON 实现对象集合的拷贝 对象定义:ObjectA属性:id,name,ageObjectB属性:id,name…...

bind failed: Address already in use
添加代码 这是个很常见的问题:在bind函数之前添加如下代码即可。 int yes 1; if (setsockopt(sockfd, SOL_SOCKET, SO_REUSEADDR, &yes, sizeof(int)) -1) { perror("setsockopt"); exit(1); } 查看端口 如果还是不能结果,那么说…...
LabVIEW结构体内部缺陷振动检测
结构体内部缺陷会改变其振动特性,通过振动分析可以检测并定位这些缺陷。本文详细分析内部缺陷对振动的影响,从频谱分析、时域分析和模态分析等多角度探讨基于LabVIEW的检测方法,提供实施步骤和注意事项,帮助工程师有效利用LabVIEW…...
RK3568技术笔记六 新建 Ubuntu Linux 虚拟机
VMware 安装完成后,启动 VMware 软件。启动后在 VMware 主界面点击“创建新的虚拟机”。如下图所示: 开始对新建的虚拟机进行设置。选择“自定义”,然后点击“下一步”。如下图所示: 使用默认配置,单击“下一步”。如下…...

Web前端博客模板下载:一站式解决方案与深度探索
Web前端博客模板下载:一站式解决方案与深度探索 在当今数字化时代,拥有一个美观且功能强大的博客网站已成为许多人的追求。而Web前端博客模板作为构建博客网站的重要工具,其选择和下载对于实现这一目标至关重要。本文将从四个方面、五个方面…...
Docker部署常见应用之大数据实时计算引擎Flink
文章目录 Flink 简介Docker 部署Docker Compose 部署参考文章 Flink 简介 Apache Flink 是一个开源的分布式流批一体化的计算框架,它提供了一个流计算引擎,能够处理有界和无界的数据流。Flink 的核心优势在于其高吞吐量、低延迟的处理能力,以…...

python使用os.getcwd()获取当前路径不正确
# codinggbk import ostry:current_dir os.getcwd()#print(os.path.dirname(os.path.realpath(__file__)))#获取错误print("当前工作目录[不想要]:",current_dir)#获取真实文件夹路径print("当前工作目录[想要]:",os.path.dirname(…...

pycharm终端pip安装模块成功但还是显示找不到 ModuleNotFoundError: No module named
报错信息: ModuleNotFoundError: No module named 但是分明已经安装过此模块: 在cmd运行pip list 查看所有安装过的包找到了安装过: 如果重新安装就是这样:显示已经存在了 问题排查: 直接根据重新安装的显示已存在的…...
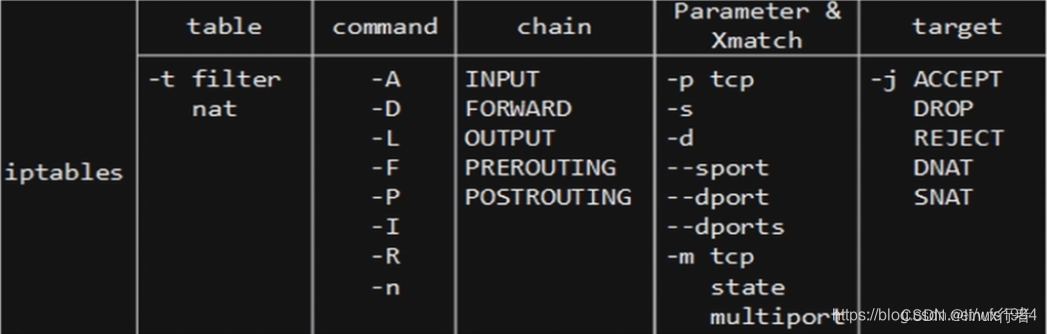
iptables教程
1 iptables安装 1.1 iptables和iptables-service的关系 iptables 是基于内核的,和 iptables-services 没有关系,不用安装任何工具包就可以使用 iptable 命令添加的防火墙规则, 但是iptables添加的规则是临时的,基于内存的&…...

破局外贸企业海外通邮难题,U-Mail邮件中继有绝招
在当今全球化的商业环境中,国内企业正扮演着越来越重要的角色,它们不仅在国内市场活跃,而且在全球范围内拓展业务,成为国际贸易中不可或缺的一部分。然而,尽管这些企业在业务扩展上取得了显著成就,但在与海…...
: 从理论到实践的指南(2))
支持向量机(SVM): 从理论到实践的指南(2)
葡萄酒数据集经常被用于机器学习、模式识别和统计分类算法的测试中。由于其特征维度较高,非常适合于验证特征选择和降维方法,例如主成分分析(PCA)或线性判别分析(LDA)的效果。同时,由于数据集包…...
——修订注释(Redaction))
PDF格式分析(八十六)——修订注释(Redaction)
修订注释(PDF 1.7及其以上版本),该注释的做用是标识要从文档中删除的内容。 修订注释启用的步骤如下: 1、内容标识。PDF编辑器可指定应删除的文档内容片段或区域,在执行下一个步骤前,用户可以看到、移动和重新定义这些注释。 2、内容移除。PDF阅读器应删除修订注释指…...

【python】flask中Session忽然取不到存储内容怎么办?
尚未确定,后续更新,先别以此为准。 【背景】 用flask写的Web应用,运行不正常,查看原因,发现视图函数a中设定的session内容在视图函数b忽然拿不到了。 【分析】 这个应用在两个服务器间互相Hook,因此可能涉及跨域的问题。 视图函数a设置的session,再次从前端调用视图…...

05-腾讯云Copilot及 向量数据库AI套件介绍
1 Andon Copilot核心功能介绍 2 Andon Copilot覆盖腾讯云售后、售前场景 3 腾讯云向量数据库– AI套件效果 AI 套件是腾讯云向量数据库(Tencent Cloud VectorDB)提供的一站式文档检索解决方案,包含自动化文档解析、信息补充、向量化、内容检…...

软件版本库管理工具
0 Preface/Foreword 常用代码版本管理工具包括如下几种: Git,最基本管理工具,由Linux kernel开发者开发Repo,主要用于管理Android SDK,由Google开发Gerrit,代码审查软件 1 Git 最基本的代码版本库管理工…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...

多模态图像修复系统:基于深度学习的图片修复实现
多模态图像修复系统:基于深度学习的图片修复实现 1. 系统概述 本系统使用多模态大模型(Stable Diffusion Inpainting)实现图像修复功能,结合文本描述和图片输入,对指定区域进行内容修复。系统包含完整的数据处理、模型训练、推理部署流程。 import torch import numpy …...

Bean 作用域有哪些?如何答出技术深度?
导语: Spring 面试绕不开 Bean 的作用域问题,这是面试官考察候选人对 Spring 框架理解深度的常见方式。本文将围绕“Spring 中的 Bean 作用域”展开,结合典型面试题及实战场景,帮你厘清重点,打破模板式回答,…...

提升移动端网页调试效率:WebDebugX 与常见工具组合实践
在日常移动端开发中,网页调试始终是一个高频但又极具挑战的环节。尤其在面对 iOS 与 Android 的混合技术栈、各种设备差异化行为时,开发者迫切需要一套高效、可靠且跨平台的调试方案。过去,我们或多或少使用过 Chrome DevTools、Remote Debug…...

通过MicroSip配置自己的freeswitch服务器进行调试记录
之前用docker安装的freeswitch的,启动是正常的, 但用下面的Microsip连接不上 主要原因有可能一下几个 1、通过下面命令可以看 [rootlocalhost default]# docker exec -it freeswitch fs_cli -x "sofia status profile internal"Name …...

【C++】纯虚函数类外可以写实现吗?
1. 答案 先说答案,可以。 2.代码测试 .h头文件 #include <iostream> #include <string>// 抽象基类 class AbstractBase { public:AbstractBase() default;virtual ~AbstractBase() default; // 默认析构函数public:virtual int PureVirtualFunct…...

JS红宝书笔记 - 3.3 变量
要定义变量,可以使用var操作符,后跟变量名 ES实现变量初始化,因此可以同时定义变量并设置它的值 使用var操作符定义的变量会成为包含它的函数的局部变量。 在函数内定义变量时省略var操作符,可以创建一个全局变量 如果需要定义…...
