破局外贸企业海外通邮难题,U-Mail邮件中继有绝招
在当今全球化的商业环境中,国内企业正扮演着越来越重要的角色,它们不仅在国内市场活跃,而且在全球范围内拓展业务,成为国际贸易中不可或缺的一部分。然而,尽管这些企业在业务扩展上取得了显著成就,但在与海外合作伙伴沟通时,却面临着一些挑战,尤其是电子邮件的国际传输问题。

电子邮件作为外贸企业与海外市场沟通的主要工具,其重要性不言而喻。但是,由于中国国家防火墙的存在、出口带宽的限制以及国内外邮箱规则的差异,邮件的国际传输并不总是顺畅。这些问题导致了邮件丢失、退信以及收发延迟,对企业的海外业务发展造成了不小的影响。
为了解决这些问题,U-Mail技术团队提出了一系列解决方案。他们建议,通过建立专用的传输通道和海外服务器的连接,并采用加密传输协议,可以有效地规避国家防火墙和出口带宽的限制。U-Mail邮件中继服务正是基于这样的理念,通过架设海外中转服务器和邮件加密传输技术,为外贸企业提供了一个全面的解决方案。
U-Mail邮件中继在全球多个重要城市,如美洲、欧洲、亚太地区,都部署了邮件中继服务器。这些服务器位于网络连接良好的数据中心,无论用户的邮件服务器接入点是电信还是联通,都能实现高速访问。此外,U-Mail采用了智能DNS技术,系统会根据用户的网络环境自动选择最佳投递线路。如果遇到投递失败的情况,系统会自动更换线路,直到邮件成功发送,确保邮件能够实时、准确地送达海外。
在安全方面,U-Mail邮件服务器支持128-256位SSL加密传输,并与对方SMTP服务器采用TLS加密传输。通过VPN技术,U-Mail在电信、联通以及海外服务器之间实现了高位加密传输。这种数据加密技术不仅可以防止邮件被国家防火墙过滤,还能压缩邮件大小,提高传输速度。
此外,U-Mail还注重邮件的反欺诈问题。他们为所有服务器设置了符合RFC标准的IP反向解析(PTR)和SMTP会话HELO参数,并提供SPF记录设置服务,以帮助企业解决邮件假冒问题。
总之,随着全球化贸易的发展,中国外贸企业面临着越来越多的挑战,其中电子邮件的国际传输问题是一个重要的方面。通过采用U-Mail邮件中继服务,可以从多方面提高企业与海外客户沟通的效率,实现更高效、更安全的国际沟通。
相关文章:

破局外贸企业海外通邮难题,U-Mail邮件中继有绝招
在当今全球化的商业环境中,国内企业正扮演着越来越重要的角色,它们不仅在国内市场活跃,而且在全球范围内拓展业务,成为国际贸易中不可或缺的一部分。然而,尽管这些企业在业务扩展上取得了显著成就,但在与海…...
: 从理论到实践的指南(2))
支持向量机(SVM): 从理论到实践的指南(2)
葡萄酒数据集经常被用于机器学习、模式识别和统计分类算法的测试中。由于其特征维度较高,非常适合于验证特征选择和降维方法,例如主成分分析(PCA)或线性判别分析(LDA)的效果。同时,由于数据集包…...
——修订注释(Redaction))
PDF格式分析(八十六)——修订注释(Redaction)
修订注释(PDF 1.7及其以上版本),该注释的做用是标识要从文档中删除的内容。 修订注释启用的步骤如下: 1、内容标识。PDF编辑器可指定应删除的文档内容片段或区域,在执行下一个步骤前,用户可以看到、移动和重新定义这些注释。 2、内容移除。PDF阅读器应删除修订注释指…...

【python】flask中Session忽然取不到存储内容怎么办?
尚未确定,后续更新,先别以此为准。 【背景】 用flask写的Web应用,运行不正常,查看原因,发现视图函数a中设定的session内容在视图函数b忽然拿不到了。 【分析】 这个应用在两个服务器间互相Hook,因此可能涉及跨域的问题。 视图函数a设置的session,再次从前端调用视图…...

05-腾讯云Copilot及 向量数据库AI套件介绍
1 Andon Copilot核心功能介绍 2 Andon Copilot覆盖腾讯云售后、售前场景 3 腾讯云向量数据库– AI套件效果 AI 套件是腾讯云向量数据库(Tencent Cloud VectorDB)提供的一站式文档检索解决方案,包含自动化文档解析、信息补充、向量化、内容检…...

软件版本库管理工具
0 Preface/Foreword 常用代码版本管理工具包括如下几种: Git,最基本管理工具,由Linux kernel开发者开发Repo,主要用于管理Android SDK,由Google开发Gerrit,代码审查软件 1 Git 最基本的代码版本库管理工…...
LVS负载均衡集群企业级应用实战-LVS/NAT模式(三)
目录 LVS/NAT模式 一. 环境准备 二. 对虚拟服务器操作 三. 对真实服务器操作 四. 打开网站验证 LVS/NAT模式 一. 环境准备 统一关闭防火墙和selinux,时间同步,配置好YUM源系统发行版选择会用就可以,这里也是两种一起使用学习。用的不同系…...
)
在Spring中如何手动开启事务(使用编程式事务)
这里写自定义目录标题 一、使用 transactionManager1、向容器中注入事务管理器2、使用 transactionManager 提交事务3、测试 二、使用TransactionTemplate1、向容器中注入 TransactionTemplate2、开启事务 一、使用 transactionManager 1、向容器中注入事务管理器 Configurat…...

cv的优势
计算机视觉(CV)技术是一种通过计算机对图像、视频等视觉数据进行分析和理解的技术。它在多个领域有着广泛的应用,包括图像识别、目标检测、人脸识别、无人驾驶等。下面是一些计算机视觉技术的优势和挑战的例子: 优势:…...

基于某评论的TF-IDF下的LDA主题模型分析
完整代码: import numpy as np import re import pandas as pd import jieba from sklearn.feature_extraction.text import TfidfVectorizer from sklearn.decomposition import LatentDirichletAllocationdf1 pd.read_csv(小红书评论.csv) # 读取同目录下csv文件…...

四、Nginx配置文件-负载均衡
目录 一、负载均衡的作用 二、负载均衡状态 三、负载均衡的指令 1、upstream 指令 2、server指令 四、负载均衡几种方式 1、轮询(Round Robin 常用) 2、IP Hash (较少) 3、最少连接数(Least Connections 较少&…...
ofd文件预览
文件列表 <template><div><div classfile v-if$myUtils.coll.isNotEmpty(filesList)><div classfile-view><div classfile-view-item :style{justifyContent: align } v-for(item, index) in filesList :keyindex><img classfile-view-item-…...
)
浅浅了解下Spring中生命周期函数(Spring6全攻略)
你好,这里是codetrend专栏“Spring6全攻略”。 Spring框架设计生命周期回调函数的主要目的是为了提供一种机制,使开发人员能够在对象创建、初始化和销毁等生命周期阶段执行特定的操作。这种机制可以帮助开发人员编写更加灵活和可维护的代码。 举个例子…...
建议收藏!亚马逊卖家必须知道的37个常用术语解释
运营亚马逊,经常会看到很多个专业术语,想必大部分新手卖家都比较陌生,熟悉这些常用术语的含义有助于你更好地运营亚马逊。下面为各位整理了37个在亚马逊跨境电商中常见的术语及其解释,建议收藏! 1、SKU Stock Keeping…...
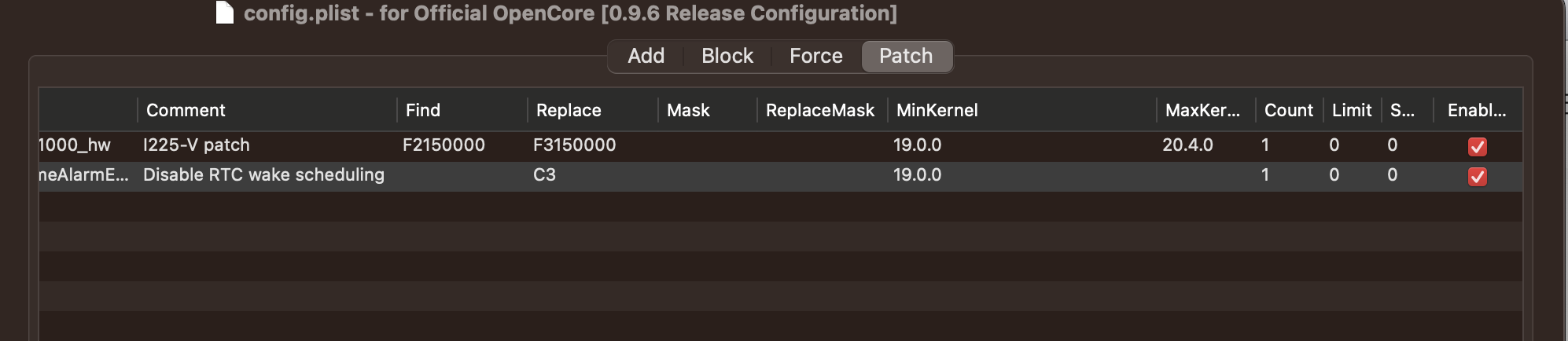
黑苹果睡眠总是自动唤醒(RTC)
黑苹果睡眠总是自动唤醒【RTC】 1. 问题2. 解决方案2.1. 查看重启日志2.2. 配置Disable RTC wake scheduling补丁 3. 后续4. 参考 1. 问题 黑苹果EFI 更换后,总是在手动 睡眠后,间歇性重启,然后再次睡眠,然后再重启。原因归结为&…...

【代码随想录训练营】【Day 49+】【动态规划-8】| Leetcode 121, 122, 123
【代码随想录训练营】【Day 49】【动态规划-8】| Leetcode 121, 122, 123 需强化知识点 买卖股票系列 题目 121. 买卖股票的最佳时机 动态规划贪心:记录左侧的最小值 class Solution:def maxProfit(self, prices: List[int]) -> int:# n len(prices)# # 0…...
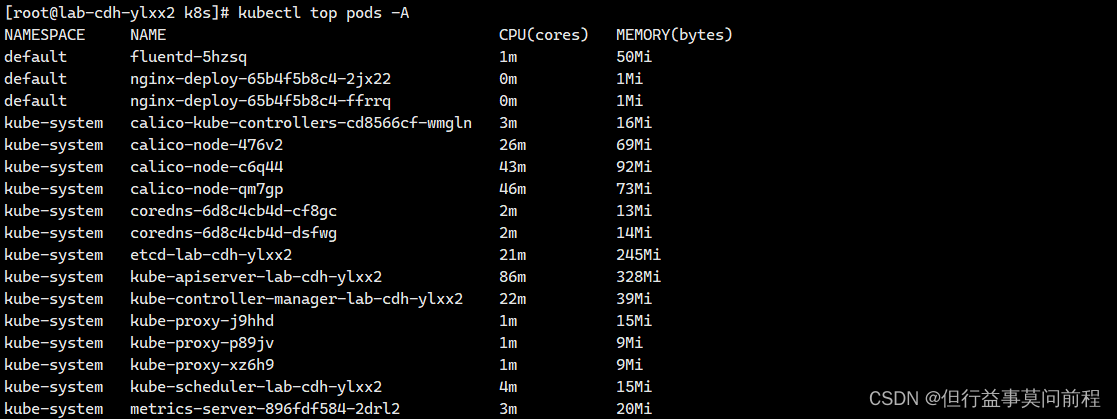
k8s metrics-server服务监控pod 的 cpu、内存
项目场景: 需要开启指标服务,依据pod 的 cpu、内存使用率进行自动的扩容或缩容 pod 的数量 解决方案: 下载 metrics-server 组件配置文件: wget https://github.com/kubernetes-sigs/metrics-server/releases/latest/download/…...

电脑自带录屏在哪?电脑录屏,4个详细方法
在现代社会中,越来越多的人需要在电脑上录制视频,比如录制游戏操作、制作教学视频、演示文稿等等。因此,电脑录屏成为了一项非常重要的功能。那么电脑自带录屏在哪?本文将带领大家看看可以使用哪些方法进行录屏。 录屏方法一&…...
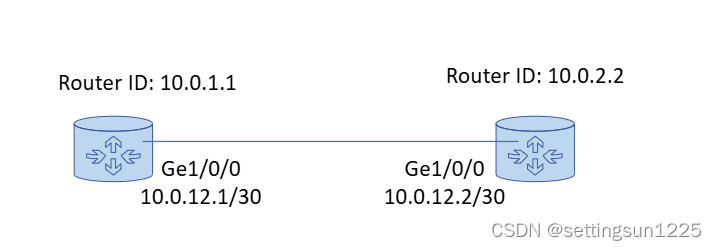
[Cloud Networking] Layer3 (Continue)
文章目录 1. DHCP Protocol1.1 DHCP 三种分配方式1.2 DHCP Relay (中继) 2. 路由协议 (Routing Protocol)2.1 RIP (Routing Information Protocol)2.2 OSPF Protocol2.2.1 OSPF Area2.2.2 Route ID / DR / BDR2.2.3 LSA / OSPF 邻居表 / LSDB / OSPF路由表 2.3 BGP Protocol2.4…...

missing authentication credentials for REST request
1、报错截图 2、解决办法 将elasticsearch的elasticsearch.yml的 xpack.security.enabled: true 改为 xpack.security.enabled: false...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...

云原生安全实战:API网关Kong的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关(API Gateway) API网关是微服务架构中的核心组件,负责统一管理所有API的流量入口。它像一座…...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...

Linux nano命令的基本使用
参考资料 GNU nanoを使いこなすnano基础 目录 一. 简介二. 文件打开2.1 普通方式打开文件2.2 只读方式打开文件 三. 文件查看3.1 打开文件时,显示行号3.2 翻页查看 四. 文件编辑4.1 Ctrl K 复制 和 Ctrl U 粘贴4.2 Alt/Esc U 撤回 五. 文件保存与退出5.1 Ctrl …...

C++ 设计模式 《小明的奶茶加料风波》
👨🎓 模式名称:装饰器模式(Decorator Pattern) 👦 小明最近上线了校园奶茶配送功能,业务火爆,大家都在加料: 有的同学要加波霸 🟤,有的要加椰果…...
