DP:两个数组的dp问题

解决两个数组的dp问题的常用状态表示:
1、选取第一个字符串[0-i]区间以及第二个字符串[0,j]区间作为研究对象
2、根据题目的要求确定状态表示
字符串dp的常见技巧
1、空串是有研究意义的,引入空串可以帮助我们思考虚拟的边界如何进行初始化。
2、如果我们的dp多开了一行一列,可以在字符串的前面多加上一个空格(s=“ ”+s),这样可以保证dp数组和字符串数组的下标映射关系是一一对应的,方便我们书写代码
一、最长公共子序列(模版)
. - 力扣(LeetCode)

算法原理:
1、状态表示(经验+题目要求)
dp[i][j]表示:s1的[0,i]区间以及s2的[0,j]区间内的所有子序列中,最长公共子序列的长度。
2、状态转移方程
dp[i][j]: (从最后一个位置的状况去分情况讨论)
(1)s[i]==s[j]——>dp[i-1][j-1]+1
(2)s[i]!=s[j]——>max(dp[i-1][j],dp[i][j-1])
注意:dp[i-1][j]和dp[i][j-1]都包含了dp[i-1][j-1]的情况,但是该题只需要找最大值而不是统计个数,所以不必在意。
3、初始化
多开一行一列,引入空串去研究边界,均初始化为0即可。
4、填表顺序
从上往下填每一行
每一行从左往右填
5、返回值
dp[m][n]
class Solution {
public:int longestCommonSubsequence(string text1, string text2) {//字符串技巧int m=text1.size(),n=text2.size();text1=" "+text1, text2=" "+text2;vector<vector<int>> dp(m+1,vector<int>(n+1));for(int i=1;i<=m;++i)for(int j=1;j<=n;++j)if(text1[i]==text2[j]) dp[i][j]=dp[i-1][j-1]+1;else dp[i][j]=max(dp[i-1][j],dp[i][j-1]);return dp[m][n];}
};二、不相交的线
. - 力扣(LeetCode)

该题其实等价于最长公共子序列
class Solution {
public:int maxUncrossedLines(vector<int>& nums1, vector<int>& nums2) {//相当于是最长公共子序列int m=nums1.size(),n=nums2.size();vector<vector<int>> dp(m+1,vector<int>(n+1));for(int i=1;i<=m;++i)for(int j=1;j<=n;++j) if(nums1[i-1]==nums2[j-1]) dp[i][j]=dp[i-1][j-1]+1;else dp[i][j]=max(dp[i-1][j],dp[i][j-1]);return dp[m][n];}
};三、不同的子序列
. - 力扣(LeetCode)

算法原理:
1、状态表示(经验+题目要求)
dp[i][j]表示:s的[0,j]区间的所有子序列中,有多少个t的[0,i]区间内的子串
2、状态转移方程
dp[i][j]: (从s的子序列最后一个位置是否包含s[j])
(1)包含s[j]——>t[i]==s[j]——>+=dp[i-1][j-1]
(2)不包含s[j]——>+=dp[i][j-1]
3、初始化
引入空串去思考:
当s和t都为空串时,应该为1
当s为空串,t不为空串的时候,应该为0
当t为空串,s不为空串的时候,应该为1
所以t为空串时,也就是i=0(第一行) 应该都初始化为1 而其他位置则是0
4、填表顺序
从上往下填每一行
每一行从左往右填
5、返回值
dp[m][n]
6、细节处理
该题可能会越界,所以用double去存储。
class Solution {
public:int numDistinct(string s, string t) {//s字符串0-j中所有子序列中 有多少个t字符串内0-i区间内的子串int m=t.size(),n=s.size();vector<vector<double>> dp(m+1,vector<double>(n+1)); //会越界 double>long long//分析最后一位的状态 t[i]==s[j] dp[i-1][j-1]//无论如何dp[i][j]+=dp[i][j-1]//可以利用空串的性质去思考for(int j=0;j<=n;++j) dp[0][j]=1; for(int i=1;i<=m;++i)for(int j=1;j<=n;++j){dp[i][j]+=dp[i][j-1];if(t[i-1]==s[j-1]) dp[i][j]+=dp[i-1][j-1];}return dp[m][n];}
};四、通配符匹配(重点)
. - 力扣(LeetCode)


class Solution {
public:bool isMatch(string s, string p) {//两个数组的dp问题//p中0-j的子串能否匹配s中0-i的子串int m=s.size(),n=p.size();s=" "+s,p=" "+p;vector<vector<bool>> dp(m+1,vector<bool>(n+1));//初始化第一行 当s为空(i=0时) dp[0][0]=true;for(int j=1;j<=n;++j) if(p[j]=='*') dp[0][j]=true;else break;for(int i=1;i<=m;++i)for(int j=1;j<=n;++j)if(p[j]=='*') dp[i][j]=dp[i-1][j]||dp[i][j-1];else dp[i][j]=(p[j]=='?'||s[i]==p[j])&&dp[i-1][j-1];return dp[m][n];}
};五、正则表达式匹配(重点)
. - 力扣(LeetCode)


class Solution {
public:bool isMatch(string s, string p) {//p中0-j的子串能否匹配s中0-i的子串int m=s.size(),n=p.size();s=" "+s,p=" "+p;//控制下标的映射vector<vector<bool>> dp(m+1,vector<bool>(n+1));//如果是 (p[j]=="."||p[j]==s[i])&&dp[i-1][j-1]//如果是 * 取决于p[j-1] p[j-1]='.' 匹配空 dp[i][j-2] 匹配1个 dp[i-1][j-2]……//所以dp[i][j]=dp[i][j-2]||dp[i-1][j-2]||dp[i-2][j-2]……//数学推导 dp[i-1][j]=dp[i-1][j-2]||dp[i-2][j-2]…… //dp[i][j]=dp[i][j-2]||dp[i-1][j] //如果p[j-1]==s[i] //初始化dp[0][0]=true;for(int j=2;j<=n;j+=2) if(p[j]=='*') dp[0][j]=true;else break;//填表for(int i=1;i<=m;++i)for(int j=1;j<=n;++j)if(p[j]=='*') dp[i][j]=dp[i][j-2]||(p[j-1]=='.'||p[j-1]==s[i])&&dp[i-1][j];else dp[i][j]=(p[j]=='.'||p[j]==s[i])&&dp[i-1][j-1];return dp[m][n];}
};六、交错字符串
. - 力扣(LeetCode)
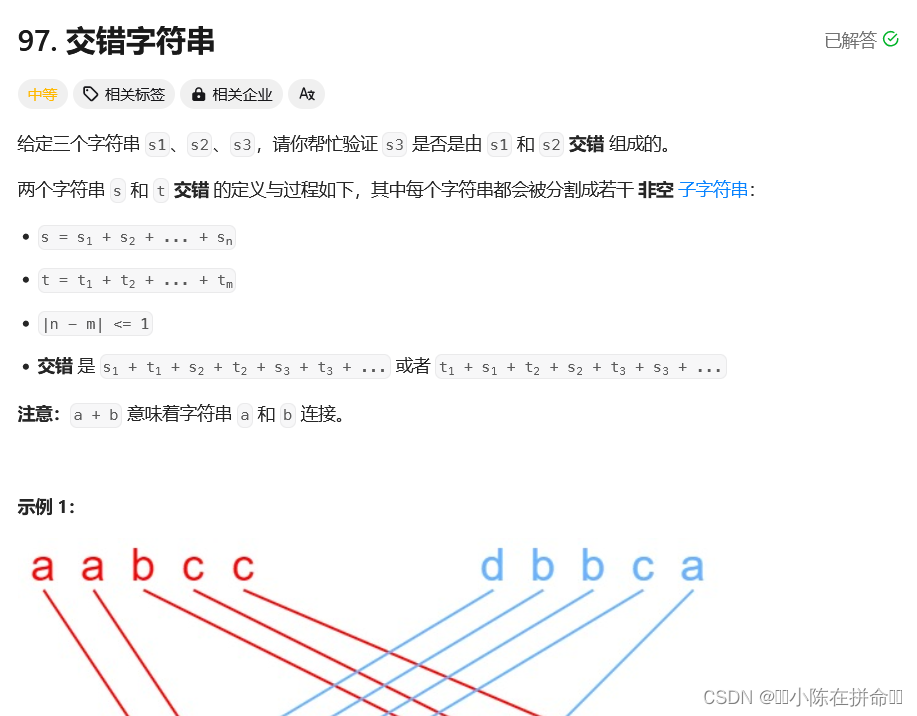
预处理:在s1、s2、s3前面加上“ ”
算法原理:
1、状态表示(经验+题目要求)
dp[i][j]表示:s1字符串的[1,i]区间和s2字符串的[1,j]区间的字符串能否拼凑成s3[1,i+j]子串
2、状态转移方程
dp[i][j]: (从最后一个位置)
dp[i][j]= s1[i]==s3[i+j]&&dp[i-1][j] ||s2[j]==s3[i+j]&&dp[i][j-1]
3、初始化
引入空串去思考:
当s1和s2均为空串时,s3也为空串,所以是true
当s1是空串,s2不是空串时,s3取决于s2 所以如果第一行一直是s2[j]==s3[j]就是true,一旦有一个不满足,就跳出循环。
当s2是空串,s1不是空串时,s3取决于s1 所以如果第一列一直是s1[i]==s3[i]就是true,一旦有一个不满足,就跳出循环。
所以需要按照上面的规则对第一行和第一列进行相关的初始化。
4、填表顺序
从上往下填每一行
每一行从左往右填
5、返回值
dp[m][n]
class Solution {
public:bool isInterleave(string s1, string s2, string s3) {int m=s1.size(),n=s2.size();if(m+n!=s3.size()) return false;//优化s1=" "+s1,s2=" "+s2,s3=" "+s3;//dp[i][j]表示s1 1-i s2 1-j 能否组成 s3 1-i+jvector<vector<bool>> dp(m+1,vector<bool>(n+1));//先初始化第一列 此时s2是空串dp[0][0]=true;for(int i=1;i<=m;++i) if(s1[i]==s3[i]) dp[i][0]=true;else break; //初始化第一行 s1是空串for(int j=1;j<=n;++j)if(s2[j]==s3[j]) dp[0][j]=true;else break;//开始填表 讨论最后一个位置 s1[i]==s[j]for(int i=1;i<=m;++i)for(int j=1;j<=n;++j) dp[i][j]=(s1[i]==s3[i+j])&&dp[i-1][j]||(s2[j]==s3[i+j])&&dp[i][j-1];return dp[m][n];}
};七、两个字符串的最小ASCII删除和
. - 力扣(LeetCode)

预处理:要求删除序列的最小ascii值,删除之后剩下的序列是一样的,并且总ascii值是不变的,所以我们可以运用正难则反的思路。
将问题转化为:求两个字符串所有最长公共子序列中的ascii码值的最大和
算法原理:
1、状态表示(经验+题目要求)
dp[i][j]表示:s1字符串的[0,i]区间和s2字符串的[0,j]区间的所有子序列里,公共子序列最大的ascii码和
2、状态转移方程
dp[i][j]: (从最后一个位置)
s1[i]==s2[j]——dp[i-1][j-1]+s1[i]
s1[i]!=s2[j]——max(dp[i-1][j],dp[i][j-1])
3、初始化
引入空串去思考:
都初始化为0即可
4、填表顺序
从上往下填每一行
每一行从左往右填
5、返回值
sum-2*dp[m][n] (sum为两个字符串的ascii码值总和)
class Solution {
public:int minimumDeleteSum(string s1, string s2) {int m=s1.size(),n=s2.size();vector<vector<int>> dp(m+1,vector<int>(n+1));//正难则反 找两个字符串的最小ascii删除和可以等价于//找两个字符串的ascii总值-两个字符串的最长公共子序列的ascii值//dp[i][j] s1 0-i 以及s2 0-j 所有子序列中最长公共子序列的ascii值总和for(int i=1;i<=m;++i)for(int j=1;j<=n;++j)if(s1[i-1]==s2[j-1]) dp[i][j]=dp[i-1][j-1]+s1[i-1];else dp[i][j]=max(dp[i-1][j],dp[i][j-1]);int sum=0;for(char&ch:s1) sum+=ch;for(char&ch:s2) sum+=ch;return sum-2*dp[m][n];}
};八、最长重复子数组
. - 力扣(LeetCode)

子数组最大的特点就是必须连续!!
算法原理:
1、状态表示(经验+题目要求)
dp[i][j]表示:nums1中以i位置为结尾的所有子数组以及nums2中以j位置为结尾的所有子数组中,最长重复子数组的长度。
2、状态转移方程
dp[i][j]: (从最后一个位置)
nums1[i]!=nums2[j]——>0
nums1[i]==nums2[j]——>dp[i-1][j-1]+1
3、初始化
都初始化为0即可
4、填表顺序
从上往下填每一行
每一行从左往右填
5、返回值
dp表中的最大值
class Solution {
public:int findLength(vector<int>& nums1, vector<int>& nums2) {int m=nums1.size(),n=nums2.size();vector<vector<int>> dp(m+1,vector<int>(n+1));//dp[i][j]表示 nums1以i位置结尾 nums2以j位置结尾的最长公共子数组长度int ret=0;for(int i=1;i<=m;++i)for(int j=1;j<=n;++j)if(nums1[i-1]==nums2[j-1]) dp[i][j]=dp[i-1][j-1]+1,ret=max(ret,dp[i][j]);return ret;}
};
相关文章:

DP:两个数组的dp问题
解决两个数组的dp问题的常用状态表示: 1、选取第一个字符串[0-i]区间以及第二个字符串[0,j]区间作为研究对象 2、根据题目的要求确定状态表示 字符串dp的常见技巧 1、空串是有研究意义的,引入空串可以帮助我们思考虚拟的边界如何进行初始化。 2、如…...

嵌入式Linux:格式化I/O
目录 1、格式化输出函数 1.1、printf()函数 1.2、fprintf()函数 1.3、dprintf()函数 1.4、sprintf()函数 1.5、snprintf()函数 2、格式化输入函数 2.1、scanf()函数 2.2、fscanf()函数 2.3、sscanf()函数 在Linux中,格式化I/O(formatted I/O&a…...
【elementui源码解析】如何实现自动渲染md文档-第二篇
目录 1.概要 2.引用文件 1)components.json 2)json-template/string 3)os.EOL 3.变量定义 4.模版填充 5.MAIN_TEMPLATE填充 6.src下的index.js文件 1)install 2)export 7.总结 1.概要 今天看第二个命令no…...
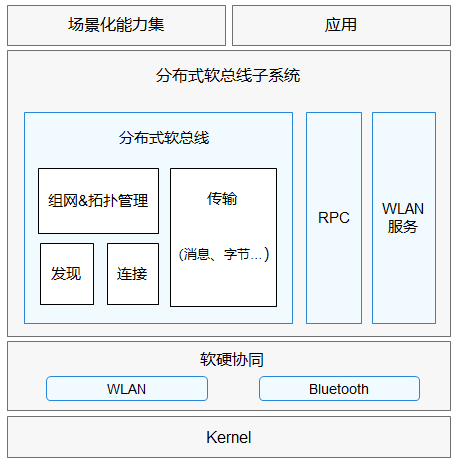
热门开源项目OpenHarmony
目录 1.概述 1.1.开源项目的意义 1.2.开源项目对软件行业的促进作用 1.3.小结 2.OpenHarmony 2.1.技术架构 2.2.分布式软总线 2.2.1.架构 2.2.2.代码介绍 2.2.2.1.代码目录 2.2.2.2.说明 2.2.2.3.发现组网和传输 2.2.2.3.1.发现 2.2.2.3.2.组网 2.2.2.3.3.传输…...

NewspaceAi之GPT使用新体验
GPT功能 使用地址:https://newspace.ai0.cn/ 上车 挂挡 踩油门,一脚到底,开始你的表演 问题1:你能做什么详细告诉我? 下面内容是GPT的回答 当然!作为一个基于GPT-4架构的AI,我能够在许多方面为…...

详解红黑树
红黑树规则 节点是红色或黑色。根节点是黑色。每个叶子节点都是黑色的空节点(NIL节点)。每个红色节点的两个子节点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点)从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。 红黑树…...

探索JavaScript逆向工程与风控等级
探索JavaScript逆向工程与风控等级 在当今的网络安全领域,JavaScript逆向工程(简称JS逆向)已成为许多开发者和安全专家关注的焦点。JS逆向主要涉及对JavaScript代码的分析与理解,以发现其内部逻辑、数据流及潜在漏洞。这种技术常用…...

C++ 22 之 立方体案例
c22立方体案例.cpp #include <iostream> #include <string>using namespace std;class Cube{ private:int cube_l; // 长int cube_w; // 宽int cube_h; // 高public:// 设置长void set_l(int l){cube_l 1;}// 设置宽void set_w(int w){cube_w w;}// 设置高void …...

vue2使用antv/g6-editor实现可拖拽流程图
依赖下载 照着这个引入就好,然后npm install 源码 <template><div id"vue-g6-editor"><el-row><el-col :span"24"></el-col></el-row><!-- 工具栏 --><el-row><el-col :span"24&qu…...

springboot学习小结
背景 业务上需要开发,组里一位前辈给我指路 spring基础 什么是spring spring提供一个容器称为spring应用上下文,容器里可以创建和管理组件,组件会在容器里装配好,组件也可以叫bean。 装配不由组件创建他依赖的组件࿰…...

vue聊天发送Emoji表情
在用web端写聊天发送表情的功能中,使用web端有系统自带的unicode表情会出现每端不统一的情况,不好用不能统一,在这里我想到了一个非常好的思路,可以解决这个问题! 那就是发送表情用图片的形式呈现,然后发给…...
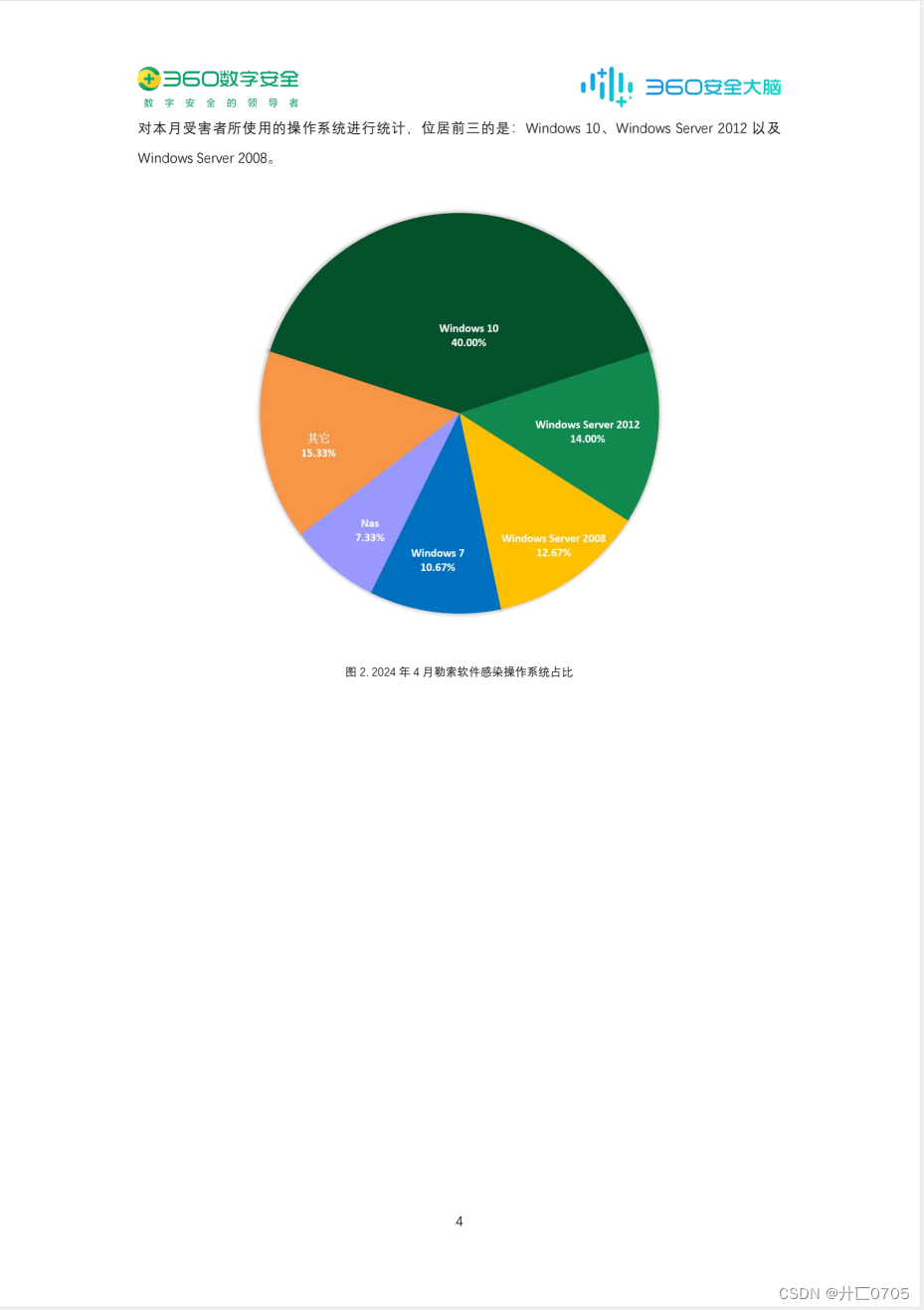
360数字安全:2024年4月勒索软件流行态势分析报告
勒索软件传播至今,360 反勒索服务已累计接收到数万勒索软件感染求助。随着新型勒索软件的快速蔓延,企业数据泄露风险不断上升,勒索金额在数百万到近亿美元的勒索案件不断出现。勒索软件给企业和个人带来的影响范围越来越广,危害性…...
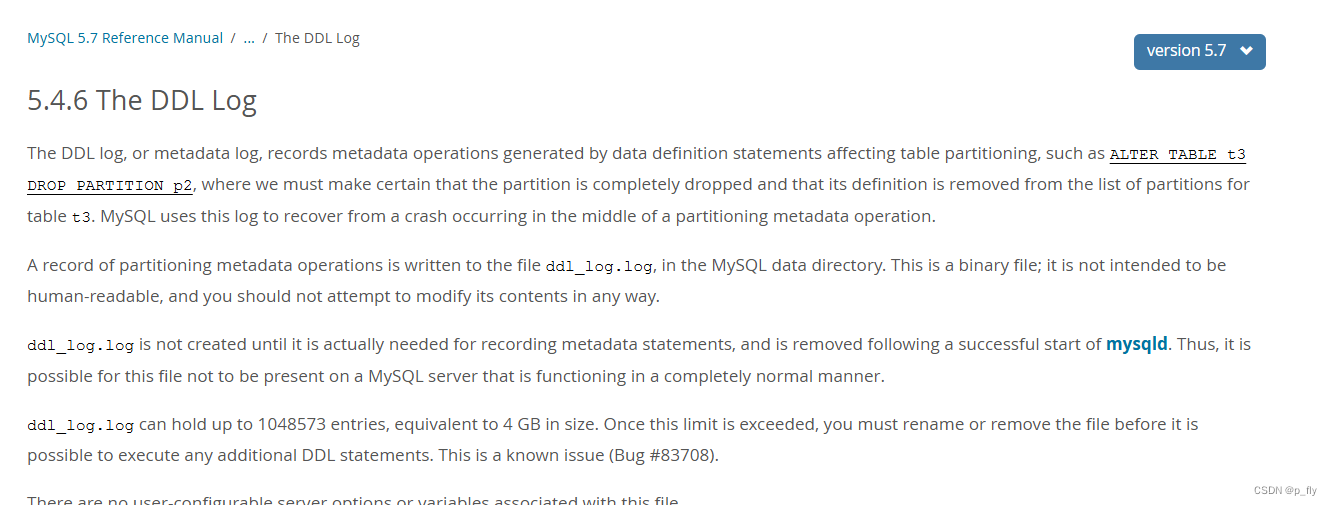
【MySQL】日志详解
本文使用的MySQL版本是8 日志概览 它们记录了数据库系统中的不同操作和事件,以便于故障排除、性能优化和数据恢复。本文将介绍MySQL中常见的几种日志,同时也会介绍一点常用的选项。 官方文档:MySQL :: MySQL 8.0 Reference Manual :: 7.4 M…...

MyBatis 延迟加载,一级缓存,二级缓存设置
MyBatis不仅提供了一级缓存和二级缓存机制,还支持延迟加载(Lazy Loading),以进一步优化性能。 1. 延迟加载(Lazy Loading) 延迟加载是在需要时才加载数据,而不是在查询时立即加载所有相关数据。…...

Linux 基本指令2
cp 指令 cp[选项]源文件 目标文件 将源文件的内容复制到目标文件中,源文件可以有多个,最后一个文件为目标文件,目标文件也可以是一段路径,若目的地不是一个目录的话会拷贝失败。若没有路径上的目录则会新建一个,若源是…...

联邦学习的基本流程,联邦学习权重聚合,联邦学习权重更新
目录 联邦学习的基本流程是 S_t = np.random.choice(range(K), m, replace=False) 联邦学习权重聚合 model.state_dict() 联邦学习权重更新 下载数据集 https://ossci-datasets.s3.amazonaws.com/mnist/train-images-idx3-ubyte.gz 联邦学习的基本流程是 **1. server初始…...
React保姆级教学
React保姆级教学 一、创建第一个react项目二、JSX基本语法与react基础知识1、 插值语法:2、 循环一个简单列表3、 实现简单条件渲染4、 实现复杂的条件渲染5、 事件绑定6、 基础组件(函数组件)7、 使用useState8、 基础样式控制9、 动态类名1…...

数据结构和矩阵细节用法:double、cell和complex #matlab
矩阵建立 建立矩阵用[]; 矩阵的同一行内的元素用逗号或者空格隔开; 矩阵的不同行的元素用分号隔开 eg. 矩阵 A 1 2 3 4 5 6 7 8 9 在matlab中矩阵A表示为: clc;clear; A[1,2,3;4,5,6;7,8,9]; %或者A[1 2 3;4 5 …...
12. Django 第三方功能应用
12. 第三方功能应用 因为Django具有很强的可扩展性, 所以延伸了第三方功能应用. 通过本章的学习, 读者能够在网站开发过程中快速实现API接口开发, 验证码生成与使用, 站内搜索引擎, 第三方网站实现用户注册, 异步任务和定时任务, 即时通信等功能.12.1 Django Rest Framework框…...
)
UnityWebRequest获取本地txt文件,其中中文乱码问题(踩坑记录)
Unity获取本地streamingassert下txt文件,遇到点问题,就是用UnityWebRequest下载一个txt文件的时候,原txt在资源管理器用notepad打开显示正常,但是Unity里调试,打印内容却是乱码, 在notepad 转存为utf-8&…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...
