机器学习实验----支持向量机(SVM)实现二分类
目录
一、介绍
(1)解释算法
(2)数据集解释
二、算法实现和代码介绍
1.超平面
2.分类判别模型
3.点到超平面的距离
4.margin 间隔
5.拉格朗日乘数法KKT不等式
(1)介绍
(2)对偶问题
(3)惩罚参数
(4)求解
6.核函数解决非线性问题
7.SMO
(1)更新w
(2)更新b
三、代码解释及其运行结果截图
(1)svm(拉格朗日、梯度、核函数)
(2)测试集预测
(3)画出超平面
四、实验中遇到的问题
五、svm的优缺点
优点:
缺点:
六、实验中还需要改进的地方
七、总代码展现
一、介绍
(1)解释算法
支持向量机(Support Vector Machine, SVM)是一类按监督学习(supervised learning)方式对数据进行二元分类的广义线性分类器(generalized linear classifier),其决策边界是对学习样本求解的最大边距超平面 ------------百度百科
本实验采取的数据集依旧是鸢尾花数据集,实现的是二分类,为了使得数据可以在坐标轴上展示出来,实验中取的是鸢尾花数据集的setosa和versicolor类别。
支持向量机SVM的目标是找到一个能够将两类数据点分隔开的超平面,使得两侧距离最近的数据点到超平面的距离最大。这些最靠近超平面的数据点被称为支持向量。
(2)数据集解释
data = pd.read_csv(r"C:\\Users\\李烨\\Desktop\\ljhg.txt", sep=' ')
X_train = data.iloc[:, :2].values
y_train = np.where(data.iloc[:, -1].values == 'setosa', 1, -1)test_data = pd.read_csv("C:\\Users\\李烨\\Desktop\\ljhgtest.txt", sep='\s+')
X_test = test_data[["Sepal.Length", "Sepal.Width"]].values采用鸢尾花数据集,为了可以在二维图上显示,所以我截取了部分数据,"Sepal.Length", "Sepal.Width"两列来表示横纵坐标,把setosa判断为正类1,把versicolor判断为负类-1
二、算法实现和代码介绍
1.超平面
两侧距离最近的数据点到超平面的距离最大。超平面被用来划分特征空间,以便实现对数据进行分类或回归。
在多分类实验中,是n元空间中,超平面就是一个n-1维的空间。 我们实现的是二分类,就得到的是一条直线。
给定样本数据集,假设样本特征为X,样本标签为y。其中y 的取值只能有+1和-1。表示样本正类和负类。
公式:
其中w代表每个特征前的系数,也就是超平面的法向量
2.分类判别模型
公式:
当f(w)>0时,判定为正类,否则判别为负类。
3.点到超平面的距离
得到样本点到超平面距离的公式:
在二维空间里面,也就是两个特征中,我们可以把超平面也就是直线的公式写成。
将一个点代入,这个点可能在直线的上方,直线上,和直线的下方。那么对于分类为正类1和负类-1,我们可以得到新的公式:
其中
4.margin 间隔
从网上找了张图便于理解

支持向量:在支持向量机中起关键作用的训练数据点。在SVM中,超平面由这些支持向量确定,它们是离分隔超平面最近的那些点。
图中l1和l3直线的确定就是按照支持向量来确定的,查找正类和负类中距离超平面最近的点,找到超平面使得这个间隔最大,以此来确定超平面。
w,b都是未知参数,所以我们就将l1和l3等比例缩放
最后得到
那么这两条直线到超平面的距离就可以表示为
那我们就可以得到预测为正类的公式
负类的公式
合并后得到
我们确定超平面是为了分隔两个类别,所以需要找到超平面到支持向量的最大距离,也就是margin间隔。也就是求两条直线到超平面距离的最大值d,也就是求||w||的最大值,为了方便计算,也就是求的的最大值。
5.拉格朗日乘数法KKT不等式
(1)介绍
拉格朗日乘数法的主要是将有等式约束条件优化问题转换为无约束条件,求解带约束条件下的极值。因为拉格朗日是求解等式约束条件,而要求解带不等式约束条件下的求解,所以引入KKT不等式约束。
对于 求解
我们可以考虑加入alpha使得,这样就可以了利用拉格朗日乘数法得到
拉格朗日得到,求解该式子对应的极值。
对该式子求导得到
为了求解f(x)在s.t条件下的极值,我们先求得不在约束条件下的极值p,然后在约束条件下查找合适的x使得他尽可能的靠近极值点,也就是说alpha就没影响等式。那么就把问题转化为
(2)对偶问题
对于求解等效于 求解
当然这样交换是假设成立。情况分为强对偶和弱对偶
如果是弱对偶,因为是先求解最小值的x,就会使得求最大值是在小中选择较大的,那么。而如果等价的话,那么就是该交换成立。特别的是,在本实验中下凸满足Slater条件,所以对于所有下凸函数都是满足强对偶性。
(3)惩罚参数
惩罚参数C控制了分类器对错误分类样本的容忍程度。较大的C值会导致分类器试图尽量减少误分类样本的数量,这可能会导致模型在训练数据上表现得更好,但也可能导致过拟合的风险增加;而较小的C值则对误分类样本的惩罚较小,允许一些样本被错分,从而使得决策边界更加平滑,减少了过拟合的风险。
我们可以预料到,数据中肯定存在一些点会影响到超平面的选择从而造成超平面的分类效果不理想,这时候就引入惩罚参数,当该点的误差超过一定界限的对其惩罚较大,就减少该样本点造成的误差。
(4)求解
最后求解极值就是用到和之前逻辑回归算法一样的梯度上升和梯度下降算法,这里就不多做介绍。
6.核函数解决非线性问题
用升维的方法来解决线性不可分的问题。
假设原始特征为x1,x2,x3,那么将这三个特征两两组合的得到:
在训练模型的适合将这些参与到训练模型中。
对于两个数据m和n,将m和n内积,然后平方得到
公式:
这个公式是多项式核函数,当时他的完整公式是
核函数有线性核函数、多项式核函数、高斯核函数等。
def polynomial_kernel(X, Y, degree=2):return (np.dot(X, Y.T) ) ** degree7.SMO
在SMO算法中,需要解决的优化问题是一个凸二次规划问题,其目标是最小化关于拉格朗日乘子alpha的二次函数,同时满足一些约束条件,例如 KKT 条件。通过构建拉格朗日函数,然后应用SMO算法来迭代优化,最终得到最优的 alpha 和 b
(1)更新w
选择两个样本i和j来进行更新,更新步长的计算与核函数的值以及拉格朗日乘子都有关系。
公式:
这个步长有正有负。当为正数的时候意味着在更新拉格朗日乘子时,朝着梯度方向移动一个较小的步长。为负数,则可能表示算法中的错误,需要检查和调整。
(2)更新b
当时 b=b1;
当时b=b2;
否则
当然a和b的更新,这边学习的仅仅只是其中的一种。
三、代码解释及其运行结果截图
(1)svm(拉格朗日、梯度、核函数)
def svm_fit(X, y, C, kernel, degree=2, alpha=0.001, num=1000):n_samples, n_features = X.shapew = np.zeros(n_samples)b = 0kernel_matrix = kernel(X, X, degree)for _ in range(num):for idx, x_i in enumerate(X):E_i = np.sum(w * y * kernel_matrix[idx]) + b - y[idx]if ((y[idx] * E_i < -alpha and w[idx] < C) or (y[idx] * E_i > alpha and w[idx] > 0)):j = np.random.choice(np.delete(np.arange(n_samples), idx))E_j = np.sum(w * y * kernel_matrix[j]) + b - y[j]w_i_old, w_j_old = w[idx], w[j]if (y[idx] != y[j]):L = max(0, w[j] - w[idx])H = min(C, C + w[j] - w[idx])else:L = max(0, w[idx] + w[j] - C)H = min(C, w[idx] + w[j])if L == H:continueeta = 2 * kernel_matrix[idx, j] - kernel_matrix[idx, idx] - kernel_matrix[j, j]if eta >= 0:continuew[j] = w[j] - (y[j] * (E_i - E_j)) / etaw[j] = max(L, min(H, w[j]))if abs(w[j] - w_j_old) < 1e-5:continuew[idx] = w[idx] + y[idx] * y[j] * (w_j_old - w[j])b1 = b - E_i - y[idx] * (w[idx] - w_i_old) * kernel_matrix[idx, idx] - y[j] * (w[j] - w_j_old) * kernel_matrix[idx, j]b2 = b - E_j - y[idx] * (w[idx] - w_i_old) * kernel_matrix[idx, j] - y[j] * (w[j] - w_j_old) * kernel_matrix[j, j]if 0 < w[idx] < C:b = b1elif 0 < w[j] < C:b = b2else:b = (b1 + b2) / 2return w, b- C是惩罚参数, kernel是代表的核函数, degree是核函数的阶数, alpha是梯度的步长, num是迭代次数。用E_i来表示的是第i个样本的预测误差,也就是样本的核函数对应的数据到超平面的距离减去该样本的分类之和。
- if ((y[idx] * E_i < -alpha and w[idx] < C) or (y[idx] * E_i > alpha and w[idx] > 0))是来判断这个是否要更新参数,如果误差太大,那么就说明w[idx]的值不合适,就需要更新他。
- 先从数据中再次随机选取一个数据,判断y[idx] != y[j],对w[j]进行约束在一定范围内,使得在满足约束条件的同时,能够使得目标函数在更新后有下降较快,可以更节省时间。
- 如果约束到一个点上面,就无法继续优化了,如果没有,二阶导数判断一下更新的方向。if eta >= 0说明图像是下凸的,跳过再次更新,为负数就需要进行整改。
- 对w进行更新,但是w应该在一定范围内。如果w[j]的改变量很小,就认为他对w[idx]的更新没有贡献,跳过。
- 根据smo更新b的方式对b进行更新。
(2)测试集预测
def predict(w, b, X_train, y_train, X_test, kernel, degree=2):predictions = []for x in X_test:prediction = bfor i, x_i in enumerate(X_train):prediction += w[i] * y_train[i] * kernel(x_i, x, degree)predictions.append(np.sign(prediction))return predictions对于测试集中的数据,将他们与训练集中的数据核函数,再根据得到的值为正数和负数分类到正类和负类。
运行结果:
可以看到对于二分类的结果还是较为准确的。

(3)画出超平面
def plot_decision_boundary(X, y, w, b, kernel, degree=2):x1_min, x1_max = X[:, 0].min() - 1, X[:, 0].max() + 1x2_min, x2_max = X[:, 1].min() - 1, X[:, 1].max() + 1xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, 0.1), np.arange(x2_min, x2_max, 0.1))Z = predict(w, b, X, y, np.c_[xx1.ravel(), xx2.ravel()], kernel, degree)Z = np.array(Z).reshape(xx1.shape)plt.contourf(xx1, xx2, Z, alpha=0.4)plt.scatter(X[:, 0], X[:, 1], c=y, marker='o', edgecolors='k')因为超平面中用到了核函数,所以超平面的公式就和样本数量有关,得到的公式就不再是可以像逻辑回归一样直接表示出来,需要最坐标轴上面的点用核函数表示 代入到公式中得到预测值。
这个代码是参考了网上的代码,以坐标轴的形式,把坐标轴上的点用核函数的公式拿去预测,那么他就得到了整张坐标轴上的分类。超平面就是两个分类交叉的地方。
运行结果:

四、实验中遇到的问题
- 实验中遇到的最主要的问题就是对w和b的更新上,因为和逻辑回归一点像,就没有真正理解算法,对w和b的选取和更新是都花了较大的时间来理解SMO的算法,SMO算法有许多给定的公式来更新w和b,核函数和拉格朗日乘子法KKT不等式等都是利用公式求解,公式较多较为复杂,重点就在对这些公式的掌握和理解上面。
- 实验中的另一个问题就是对于惩罚参数的选取上,由于刚开始看到的并没有添加惩罚参数,所以导致超平面受到的影响较大,受到个别点的影响,导致拟合效果非常不好,而且由于是利用梯度求解,所以就会导致超平面因为拟合效果不好。如图。超平面并不能很好的划分。

3.超平面的画法上面,最开始是想直接将点表示出来,但是发现用核函数得到的超平面公式与样本点的数量有关系,在画超平面的时候仍然需要对他进行核函数求解,所以在预测的时候加上核函数就可以了。
五、svm的优缺点
优点:
逻辑回归主要是处理线性问题,与之相比,支持向量机可以处理许多非线性的问题,SVM 找到最大间隔超平面,这意味着它试图最大化类别之间的间隔,拟合效果会更好。在高维空间中svm支持向量机的适应效果回归更好。
缺点:
支持向量机svm的优化问题通常是凸优化问题,它的计算复杂度随着样本数量和特征维度的增加而增加。在处理大规模数据和高维数据时,训练时间和内存时间复杂度很大。
六、实验中还需要改进的地方
- 与逻辑回归一样,使用的是普通梯度,而随机梯度上升在每次迭代中只需要计算一个样本数据的梯度,因此通常比梯度上升更快。我们可以利用随机梯度来减小时间复杂度。
- 由于对SMO算法的不熟悉,所以我的实验中用到的是最简单的SMO,复杂度高,程序预测效果没那么好,使用更加完整成熟的SMO算法可以有效改进拟合效果。
七、总代码展现
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
def polynomial_kernel(X, Y, degree=2):return (np.dot(X, Y.T) ) ** degree
def svm_fit(X, y, C, kernel, degree=2, alpha=0.001, num=1000):n_samples, n_features = X.shapew = np.zeros(n_samples)b = 0kernel_matrix = kernel(X, X, degree)for _ in range(num):for idx, x_i in enumerate(X):E_i = np.sum(w * y * kernel_matrix[idx]) + b - y[idx]if ((y[idx] * E_i < -alpha and w[idx] < C) or (y[idx] * E_i > alpha and w[idx] > 0)):j = np.random.choice(np.delete(np.arange(n_samples), idx))E_j = np.sum(w * y * kernel_matrix[j]) + b - y[j]w_i_old, w_j_old = w[idx], w[j]if (y[idx] != y[j]):L = max(0, w[j] - w[idx])H = min(C, C + w[j] - w[idx])else:L = max(0, w[idx] + w[j] - C)H = min(C, w[idx] + w[j])if L == H:continueeta = 2 * kernel_matrix[idx, j] - kernel_matrix[idx, idx] - kernel_matrix[j, j]if eta >= 0:continuew[j] = w[j] - (y[j] * (E_i - E_j)) / etaw[j] = max(L, min(H, w[j]))if abs(w[j] - w_j_old) < 1e-5:continuew[idx] = w[idx] + y[idx] * y[j] * (w_j_old - w[j])b1 = b - E_i - y[idx] * (w[idx] - w_i_old) * kernel_matrix[idx, idx] - y[j] * (w[j] - w_j_old) * kernel_matrix[idx, j]b2 = b - E_j - y[idx] * (w[idx] - w_i_old) * kernel_matrix[idx, j] - y[j] * (w[j] - w_j_old) * kernel_matrix[j, j]if 0 < w[idx] < C:b = b1elif 0 < w[j] < C:b = b2else:b = (b1 + b2) / 2return w, bdef predict(w, b, X_train, y_train, X_test, kernel, degree=2):predictions = []for x in X_test:prediction = bfor i, x_i in enumerate(X_train):prediction += w[i] * y_train[i] * kernel(x_i, x, degree)predictions.append(np.sign(prediction))return predictionsdef plot_decision_boundary(X, y, w, b, kernel, degree=2):x1_min, x1_max = X[:, 0].min() - 1, X[:, 0].max() + 1x2_min, x2_max = X[:, 1].min() - 1, X[:, 1].max() + 1xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, 0.1), np.arange(x2_min, x2_max, 0.1))Z = predict(w, b, X, y, np.c_[xx1.ravel(), xx2.ravel()], kernel, degree)Z = np.array(Z).reshape(xx1.shape)plt.contourf(xx1, xx2, Z, alpha=0.4)plt.scatter(X[:, 0], X[:, 1], c=y, marker='o', edgecolors='k')data = pd.read_csv(r"C:\\Users\\李烨\\Desktop\\ljhg.txt", sep=' ')
X_train = data.iloc[:, :2].values
y_train = np.where(data.iloc[:, -1].values == 'setosa', 1, -1)test_data = pd.read_csv("C:\\Users\\李烨\\Desktop\\ljhgtest.txt", sep='\s+')
X_test = test_data[["Sepal.Length", "Sepal.Width"]].values
y_test = test_data[["Species"]].values;C = 1.0
degree = 2
tol = 0.001
max_iter = 1000w, b = svm_fit(X_train, y_train, C, polynomial_kernel, degree, tol, max_iter)predictions = predict(w, b, X_train, y_train, X_test, polynomial_kernel, degree)cnt=0.0
for i, prediction in enumerate(predictions):if prediction == 1:ans='setosa'else :ans='versicolor'print(f"第{i}个数据{X_test[i]}预测结果为{ans},实际结果为{y_test[i]}")if ans==y_test[i]:cnt+=1print(f"准确率为{cnt/len(predictions)}")plt.rcParams['font.sans-serif'] = ['SimHei']
plt.figure(figsize=(10, 6))
plot_decision_boundary(X_train, y_train, w, b, polynomial_kernel, degree)
plt.title('SVM支持向量机')
plt.xlabel('Sepal Length')
plt.ylabel('Sepal Width')
plt.show()相关文章:

机器学习实验----支持向量机(SVM)实现二分类
目录 一、介绍 (1)解释算法 (2)数据集解释 二、算法实现和代码介绍 1.超平面 2.分类判别模型 3.点到超平面的距离 4.margin 间隔 5.拉格朗日乘数法KKT不等式 (1)介绍 (2)对偶问题 (3)惩罚参数 (4)求解 6.核函数解决非线性问题 7.SMO (1)更新w (2)更新b 三、代…...
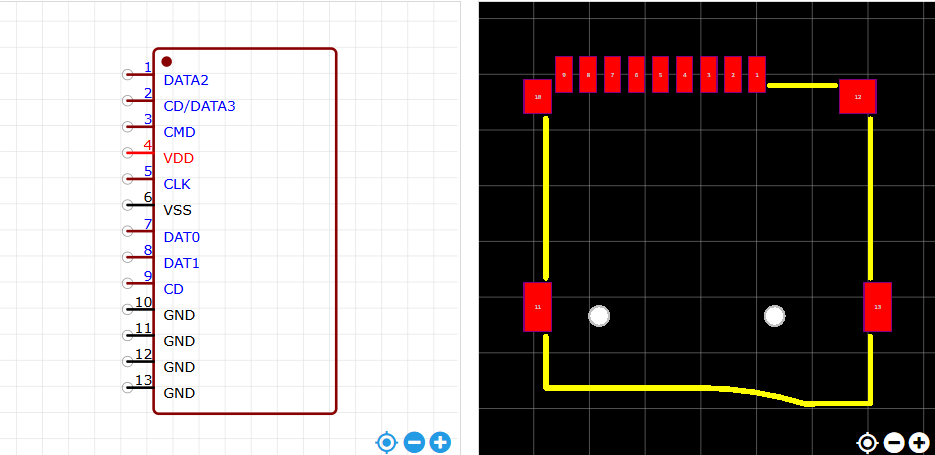
STM32自己从零开始实操05:接口电路原理图
一、TTL 转 USB 驱动电路设计 1.1指路 延续使用芯片 CH340E 。 实物图 实物图 原理图与封装图 1.2数据手册重要信息提炼 1.2.1概述 CH340 是一个 USB 总线的转接芯片,实现 USB 与串口之间的相互转化。 1.2.2特点 支持常用的 MODEM 联络信号 RTS(请…...

git子模块
1 子模块管理的关键文件和配置 在 Git 中使用子模块时,Git 会利用几个特殊的文件和配置来管理子模块。以下是涉及子模块管理的关键文件和配置: 1.1 .gitmodules 这是一个文本文件,位于 Git 仓库的根目录下。它记录了子模块的信息ÿ…...

stm32编写Modbus步骤
1. modbus协议简介: modbus协议基于rs485总线,采取一主多从的形式,主设备轮询各从设备信息,从设备不主动上报。 日常使用都是RTU模式,协议帧格式如下所示: 地址 功能码 寄存器地址 读取寄存器…...

基于 Transformer 的大语言模型
语言建模作为语言模型(LMs)的基本功能,涉及对单词序列的建模以及预测后续单词的分布。 近年来,研究人员发现,扩大语言模型的规模不仅增强了它们的语言建模能力,而且还产生了处理传统NLP任务之外更复杂任务…...

证照之星是一款很受欢迎的证件照制作软件
证照之星是一款很受欢迎的证件照制作软件,证照之星可以为用户提供“照片旋转、裁切、调色、背景处理”等功能,满足用户对证件照制作的基本需求。本站证照之星下载专题为大家提供了证照之星电脑版、安卓版、个人免费版等多个版本客户端资源,此…...
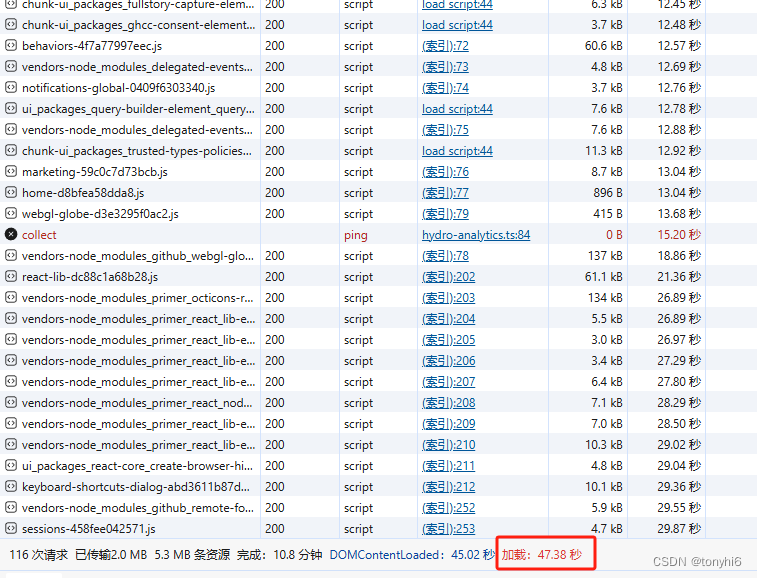
不定时更新 解决无法访问GitHub github.com 打不开 dns访问加速
1 修改hosts Windows 10为例,文件C:\Windows\System32\drivers\etc\hosts 管理员打开记事本来修改 文件-打开-“C:\Windows\System32\drivers\etc\hosts” 20.205.243.168 api.github.com 185.199.108.154 github.githubassets.com 185.199.108.133 raw.githubusercontent.…...

单向环形链表的创建与判断链表是否有环
单向环形链表的创建与单向链表的不同在于,最后一个节点的next需要指向头结点; 判断链表是否带环,只需要使用两个指针,一个步长为1,一个步长为2,环状链表这两个指针总会相遇。 如下示例代码: l…...
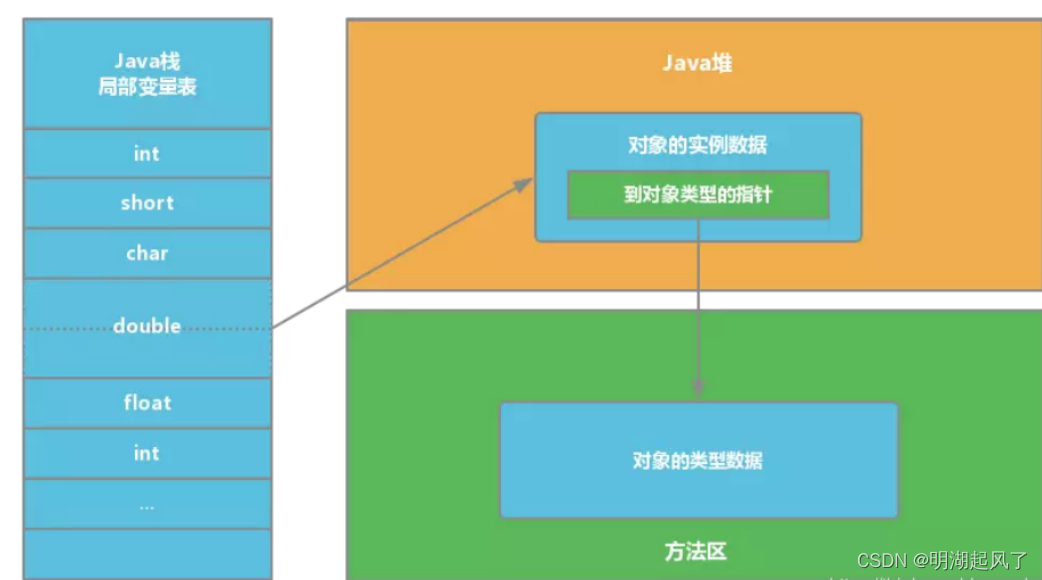
JVM堆栈的区别、分配内存与并发安全问题、对象定位
一、堆和栈的区别 堆(Heap)和栈(Stack)是两种基本的数据结构,它们在内存管理、程序执行流程控制等方面扮演着重要角色。在编程语言尤其是Java这样的高级语言环境中,堆和栈的概念被用来描述程序运行时的内存…...
)
Python教程:机器学习 - 百分位数(4)
什么是百分位数? 统计学中使用百分位数(Percentiles)为您提供一个数字,该数字描述了给定百分比值小于的值。 例如:假设我们有一个数组,包含住在一条街上的人的年龄。 ages [5,31,43,48,50,41,7,11,15,3…...
数据结构习题(快期末了)
一个数据结构是由一个逻辑结构和这个逻辑结构上的一个基本运算集构成的整体。 从逻辑关系上讲,数据结构主要分为线性结构和非线性结构两类。 数据的存储结构是数据的逻辑结构的存储映像。 数据的物理结构是指数据在计算机内实际的存储形式。 算法是对解题方法和…...

Http协议:Http缓存
文章目录 Cookie和Session缓存有效性检查整体流程总结Cookie和Session Cookie 客户端的缓存 Session 服务端的缓存,存储服务器与客户端一次会话的过程中的数据/资源 两者区别 是服务端与客户端的不同需求造成的 有效期 Cookie的有效期很长,Session的较短 原因:服务…...

idea插件开发之hello idea plugin
写在前面 最近一直想研究下自定义idea插件的内容,这样如果是想要什么插件,但又一时找不到合适的,就可以自己来搞啦!这不终于有时间来研究下,但过程可谓是一波三折,再一次切身体验了下万事开头难。那么&…...

Sm4【国密4加密解密】
当我们开发金融、国企、政府信息系统时,不仅要符合网络安全的等保二级、等保三级,还要求符合国密的安全要求,等保测评已经实行很久了,而国密测评近两年才刚开始。那什么是密码/国密?什么是密评?本文就关于密…...

git如果将多次提交压缩成一次
将N个提交压缩到单个提交中有两种方式: git reset git reset的本意是版本回退,回退时可以选择保留commit提交。我们基于git reset的作用,结合新建分支,可以实现多次commit提交的合并。这个不需要vim编辑,很少有冲突。…...

android用Retrofit进行网络请求和解析
Retrofit 的原理 Retrofit的核心原理包括动态代理与Service Method的构建、注解解析与请求配置、网络请求执行与响应处理等。它是一个类型安全的HTTP客户端,用于Android和Java平台,通过将HTTP API转化为Java接口的方式,简化了网络请求的编写…...

list容器的基本使用
目录 前言一,list的介绍二,list的基本使用2.1 list的构造2.2 list迭代器的使用2.3 list的头插,头删,尾插和尾删2.4 list的插入和删除2.5 list 的 resize/swap/clear 前言 list中的接口比较多,与string和vector类似&am…...

34万汉语词语成语反义词ACCESS\EXCEL数据库
反义词就是两个意思相反的词,包括:绝对反义词和相对反义词。分为成对的意义相反、互相对立的词。如:真——假,动——静,拥护——反对。这类反义词所表达的概念意义互相排斥。或成对的经常处于并举、对待位置的词。如&a…...

yum方式更新Jenkins
目的 使用yum方式更新Jenkins。 步骤 查看最新可用版本 $ yum list jenkins Last metadata expiration check: 0:03:44 ago on Fri Jun 14 06:10:01 2024. Installed Packages jenkins.noarch 2.452.1-1.1 jenkins Available Pa…...

欢乐钓鱼大师保姆级教程,云手机辅助攻略解析!
在这份攻略中,我们将为大家详细介绍如何在《欢乐钓鱼大师》中快速提升钓鱼技能和游戏进展,避免常见的新手误区和不必要的资源浪费。无论是钓鱼点的选择、装备的合理使用还是技能的优化,我们都会一一为您详细解析,帮助您成为一名优…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...
