机器学习与数据挖掘知识点总结(二)分类算法
目录
1、什么是数据挖掘
2、为什么要有数据挖掘
3、数据挖掘用在分类任务中的算法
朴素贝叶斯算法
svm支持向量机算法
PCA主成分分析算法
k-means算法
决策树
1、什么是数据挖掘
数据挖掘是从大量数据中发现隐藏在其中的模式、关系和规律的过程。它利用统计学、机器学习和数据库技术等工具和方法来分析大规模数据集,以发现其中的信息,并将其转化为可用的知识或决策支持。数据挖掘常用于预测、分类、聚类和关联规则发现等任务。
2、为什么要有数据挖掘
数据挖掘的出现是为了解决大规模数据中存在的隐含信息和规律,并将其转化为可用的知识或决策支持。
3、数据挖掘主要任务
通过数据挖掘技术,可以从大规模数据中挖掘出有用的信息和知识,为决策提供支持和指导,发现数据中的潜在规律和趋势。

4、数据分析步骤

5、数据挖掘用在分类任务中的算法
-
朴素贝叶斯算法
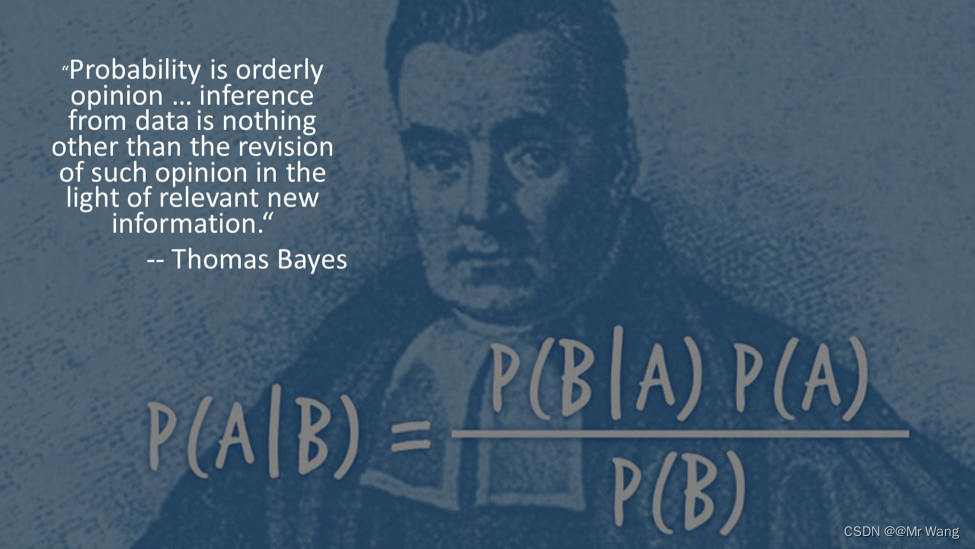
朴素贝叶斯是一组基于贝叶斯定理的监督学习算法。
先验概率:基于统计规律,基于以往的历史经验和分析得到的结果,不依赖于当前发生的条件。
后验概率:由条件概率推理而来,由因推果,是计算在发生某事之后的概率,依赖于当前发生的条件。
条件概率:记事件A发生的概率为P(A),事件B发生的概率为P(B),则在事件B发生的条件下事件A发生的概率为P(A|B),
而贝叶斯公式就是基于条件概率,通过P(B|A)求解P(A|B) ,如下:
由联合公式可以推导如下,
P(A)和P(B)分别为先验概率,P(A|B)和P(B|A)分别为后验概率,P(A,B)则称为联合概率。
全概率公式:表示若事件构成一个完备事件组且都有正概率,则对任意一个事件B都有公式成立,故有:
机器学习的最终目标就是回归或者是分类,都可以看为是预测,分类则是预测属于某一类的概率是多大,因此可以把上述贝叶斯表达式中的A看成是属于某类的规律,把B看成是具有某种特征的现象,那么贝叶斯公式又可以表示为:
朴素贝叶斯算法的原理:
特征条件假设:若假设各个特征之间没有联系,给定训练数据集后,每个样本都是n维特征,,类别标记中有m种类别,
。
朴素贝叶斯算法对条件概率分布做出了独立性的假设,即个人维度上的特征相互独立,那么在此假设前提下,条件概率可转化为:
朴素贝叶斯算法是一组基于贝叶斯定理的监督学习算法,朴素贝叶斯算法通过预测指定样本属于特定类别的概率来预测该样本的所属类别,即:
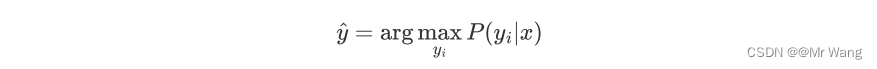
可以写为,
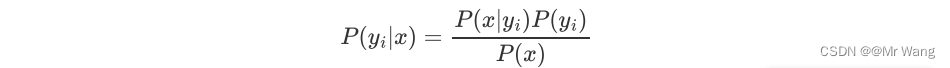 其中,
其中,对应为样本的特征向量,p(x)为样本的先验概率,对于特定样本x和任意类别yi,P(x)的取值均相同,并不会影响P(yi|x)取值的相对大小,因此在计算中可以被忽略(求解P(yi|x)就相当于求解P(x|yi)P(yi))。“朴素”特别之处就在于假设了特征
相互独立,由此可以得到:
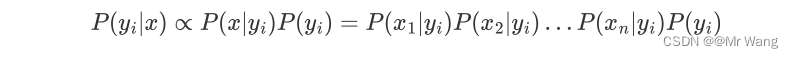
上述等式的右边即为连乘,将等式右边的概率称为判定函数。它的结果值不仅仅是代表概率,代表着判定值,,以及
均可以通过训练样本统计得到,最后的目标函数如下,
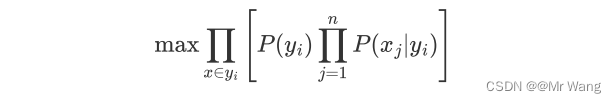
但是由于概率值为[0,1]的数,作连乘运算时,容易让最后的结果越来越趋近于0(数据下溢),故对其取log是一个常用的手段,并根据log(xy)=log(x)+log(y)将其转换为相加的形式,
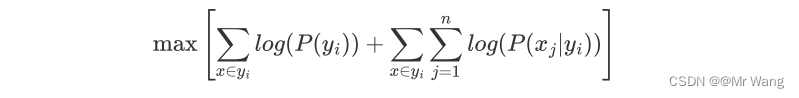
这样仅能预测出最后对应的最大的判定值,将上式中的max更改为argmax即可求出最大判定值所对应的类别。
-
svm支持向量机算法
支持向量机(Support Vector Machine,SVM)本身是一个二分类算法,是对感知器算法模型的一种扩展,现在的SVM算法支持线性分类和非线性分类的应用,并且也能通过将SVM应用于回归应用中,在不考虑集成学习算法,不考虑特定数据集时,分类算法SVM是非常优秀的。
支持向量:离分割超平面最近的那些点。
间隔:数据点到分割超平面的间距。
首先介绍一下感知器模型,感知器的思想就是在数据是线性可分(能找到一个平面将两组数据给分开)的前提下任意空间中,感知器需要寻找一个超平面,能够把所有的二分类别分割开。
感知器模型如下,目标是找到一个为0的超平面,然后分别根据神经元的加权求和的结果判断,大于0的为一个类别,小于0的为一个类别,因此,期望分类错误的样本离超平面的距离之和最小,从而让分类错误的样本更快地朝着正确的方向进行更新,从而让训练成功。
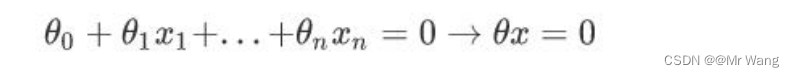
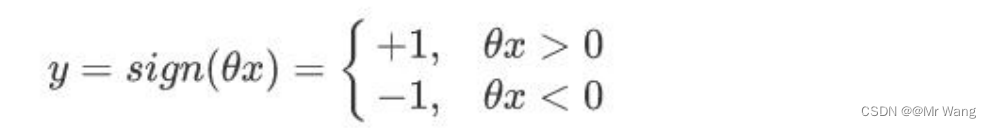
然后就是SVM算法,为什么感知器算法缺陷呢,下图中两条直线分别为感知器算法的超平面,它比较关注的是让所有的点离超平面尽可能的远,但实际上离超平面足够远的点基本都是被正确分类的,所以这个是没有意义的,反而应该关注那些离超平面很近的点,这些点才容易出错。如果测试时来了一个新的数据点(样本),并位于这两条蓝色直线之间,那么就不能很好的处理这个新的数据,由此引入了SVM支持向量机算法。

也就是说,如下图所示,希望 找到一个最好的w和b固定一个超平面,使得这个超平面在能够完美的区分正负例(分类)的基础上,找到距离最近的点间隔最大。(后面的证明过程先不叙述,涉及到拉格朗日优化目标函数过程)
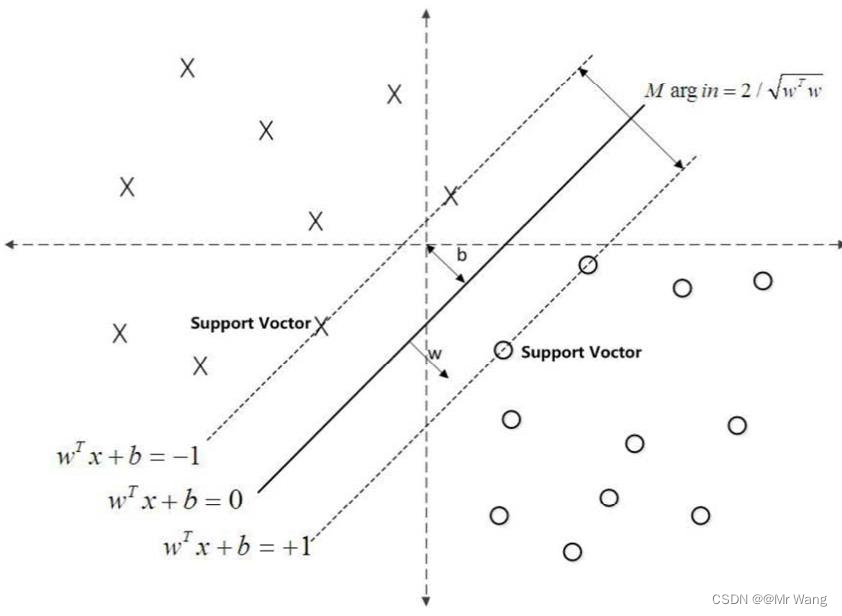
-
PCA主成分分析算法
PCA是一种线性降维方法,他的思想主要是依靠将数据从高维空间映射到低维空间,同时在低维空间里的数据的方差被最大化。
算法步骤:
- 建立数据的协方差矩阵
- 计算矩阵的多个特征向量
- 对应有最大几个特征值的特征向量被应用于重新建立数据,这样就会使新建的数据包含有大量原本数据的方差(信息量)。
主要包含最大投影方差和最小投影距离两种方法证明PCA的有效性,下面用最大投影方差的方法证明一下。
最大投影方差(证明)
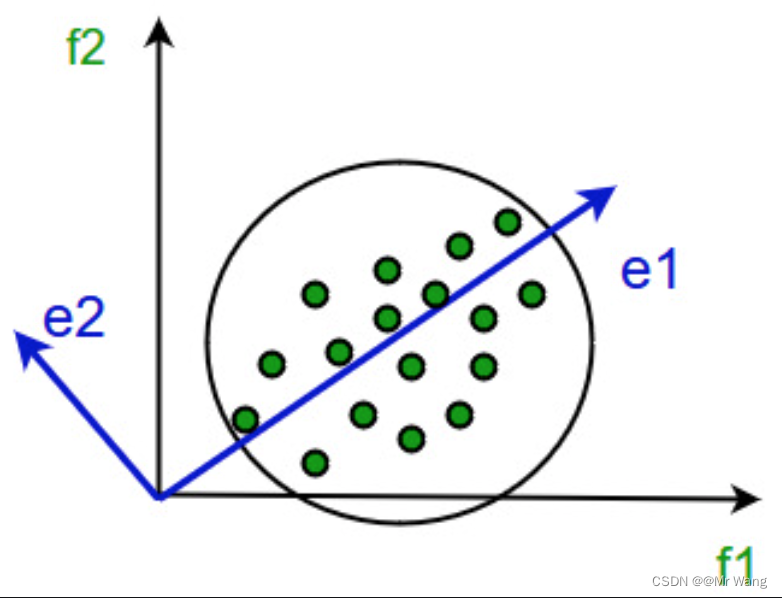
数据的离散性越大,代表数据在所投影的维度具有更高的区分度,这个区分度(方差)就是信息量,我们希望降维之后还能更多的保留原来的信息量,而且降维后不同维度的相关性为0,这样即使是去掉某些相对不重要的维度也不会干扰到剩余的维度信息。
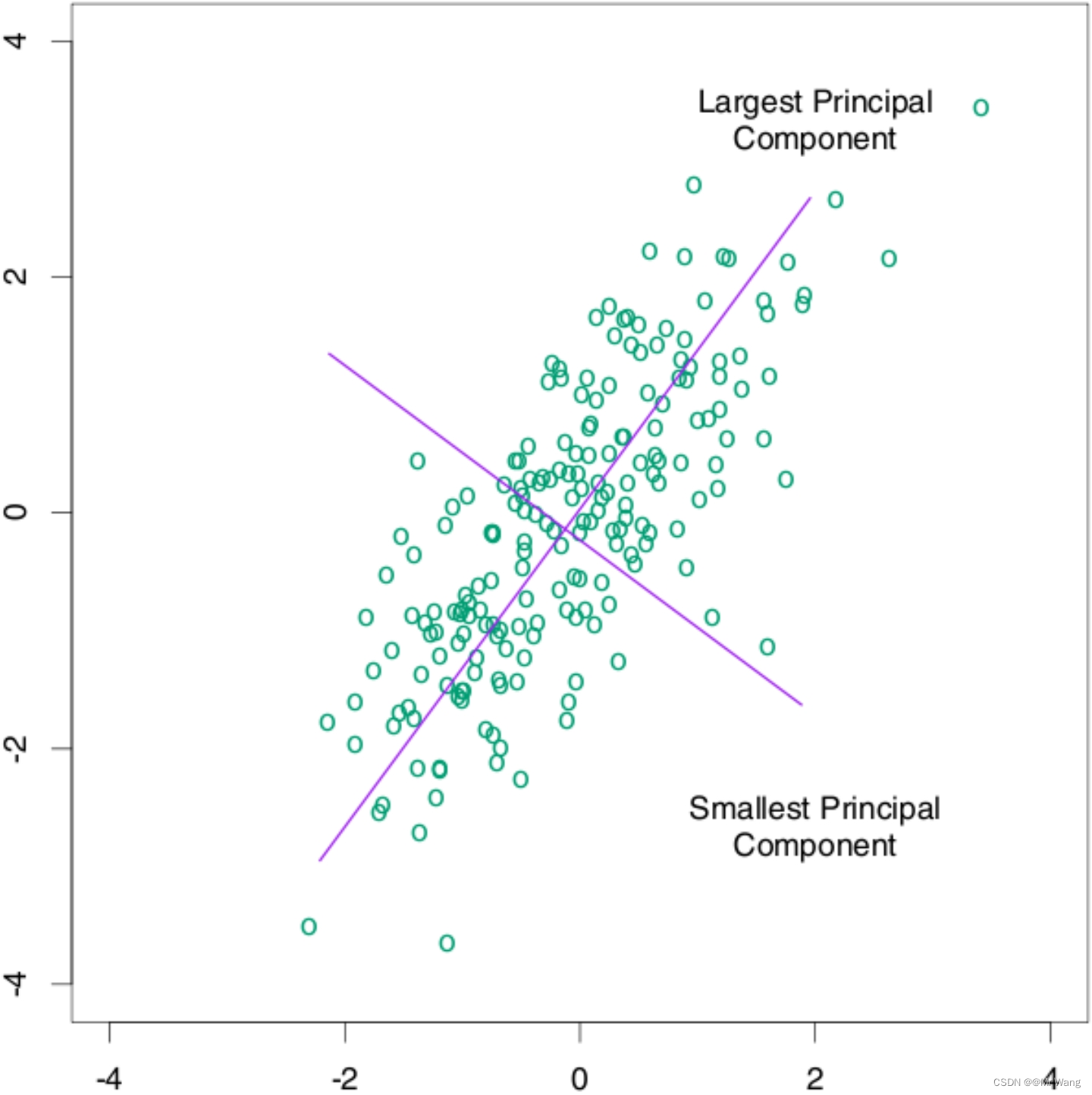
如图2所示,使用PCA主成分分析,并不会改变原始数据的分布,只是换个角度解决问题,本质上相当于是重新定义坐标系,找到一个更好的角度去审视数据。如图2,举个例子,对于同一数据分布,原坐标系横轴纵轴比例为(5:5)1:1,采用等长的横纵坐标,但经过重新找定坐标系(图2中紫色),新的坐标系横纵轴比例可能为7:3,那这样的话,采用主成分分析PCA,选取占比70%这条轴线进行降维,这就可以在降维的同时保留较大的信息量。
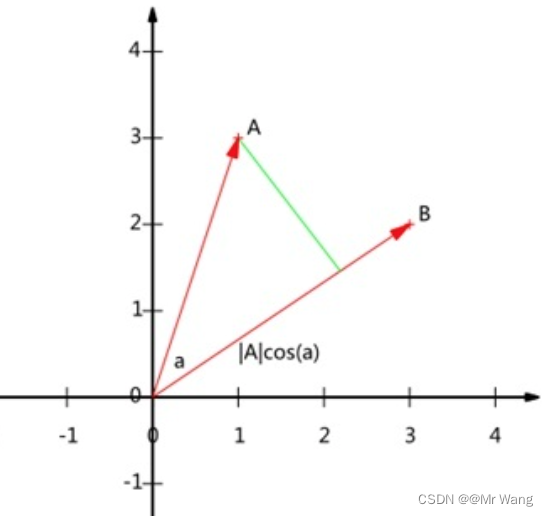
既然希望用样本点投影的方式希望投影之后的数据点会有更大的方差,那么不妨把投影之后的数值表达出来,如图3中的一个数据点A(x1,y1),将原点O与其的连线构成的向量A投影到向量B所在的方向上,得:
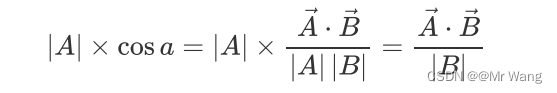
那既然这样的话,单位向量不也能表示方向吗,让B为单位向量,|B|=1,可由上式推出,
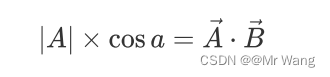
投影之后的新坐标系,每个轴用单位向量表示,新坐标系设置为标准正交基;即既保证了每个主成分向量wi的模为1,即
,又保证了各个主成分之间互不干扰(不叠加、不覆盖),
。
对于任意一个点xi投影到某个坐标轴w上,则投影后的值为。

由上面的方差公式可以推出,
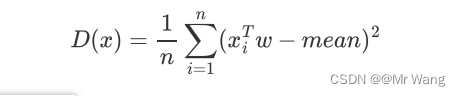
其中,mean表示投影后的均值。
又因为PCA会对未投影前的原始数据进行标准归一化操作:
- 均值归一化/中心化:经过如下证明得投影后的mean也为0.
- 方差归一化:即为无量纲化,归一到某范围内,这样在投影之后方差不会受到某些维度的主导。
故将mean=0带入计算方差的式子中得,
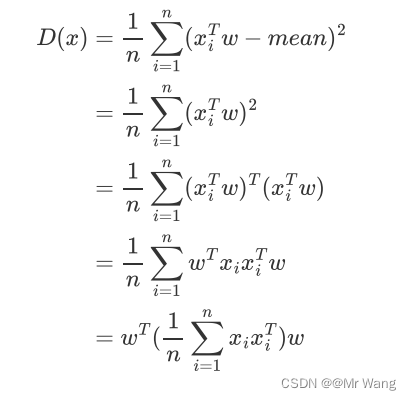
注意,在前面是两个向量的内积运算,在上述式子中,xi被看成为一个列向量,因此
((m*n)*(n*m)=m*m),接着把上面的每个样本点运算求和转换为原始数据X(shape:d*n,d指原始数据维度,n代表原始数据的样本数),得
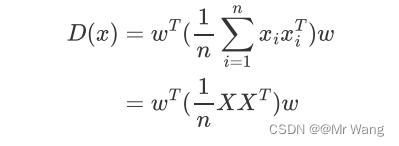
接着代入协方差(用来衡量两个随机变量之间关系的统计量,通过计算变量之间的协方差矩阵,可以找到数据中最具代表性和最重要的方向(主成分))公式中得,
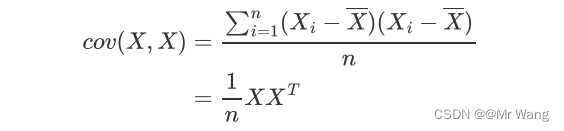
若将协方差矩阵用符号表示,则优化目标最大化投影后方差等价于,
![]()
然后按照构建拉格朗日函数,g(x)为约束条件,引入拉格朗日乘子lamda,这样就把具有约束条件的最优问题转化为无约束条件的最优化问题,对w求偏导得,
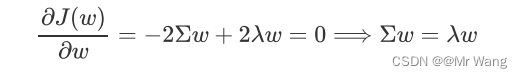
这样就可以看出,w是 的特征向量,lamda是对应特征向量的特征值,最大化投影后的方差,等价于
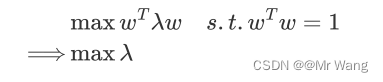
这样一来,要寻找的第一主成分就是使得投影方差最大的坐标轴就是最大特征值对应的特征向量。最终保留几个维度,就按照大小顺序选取前几个最大的特征值对应的特征向量,然后把原始数据进行投影即可,比如取出前k个大的特征值对应的特征向量w1,w2,...,wk,通过以下映射将d维样本降低到k维度,
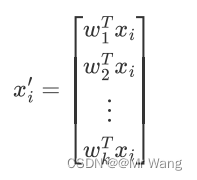
如此一来,新的的第j维就是xi在第j个主成分wj方向上的投影,如果通过选取最大的k个特征值对应的特征向量,将方差小的特征抛弃,使得每个d维列向量xi被映射为k维列向量xi',
和
为对应维度上的方差,那么定义降维后的信息占比如下,可以反过来通过
决定该选择保留下多少维度:
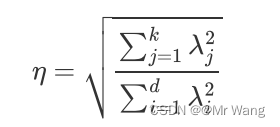
-
k-means算法
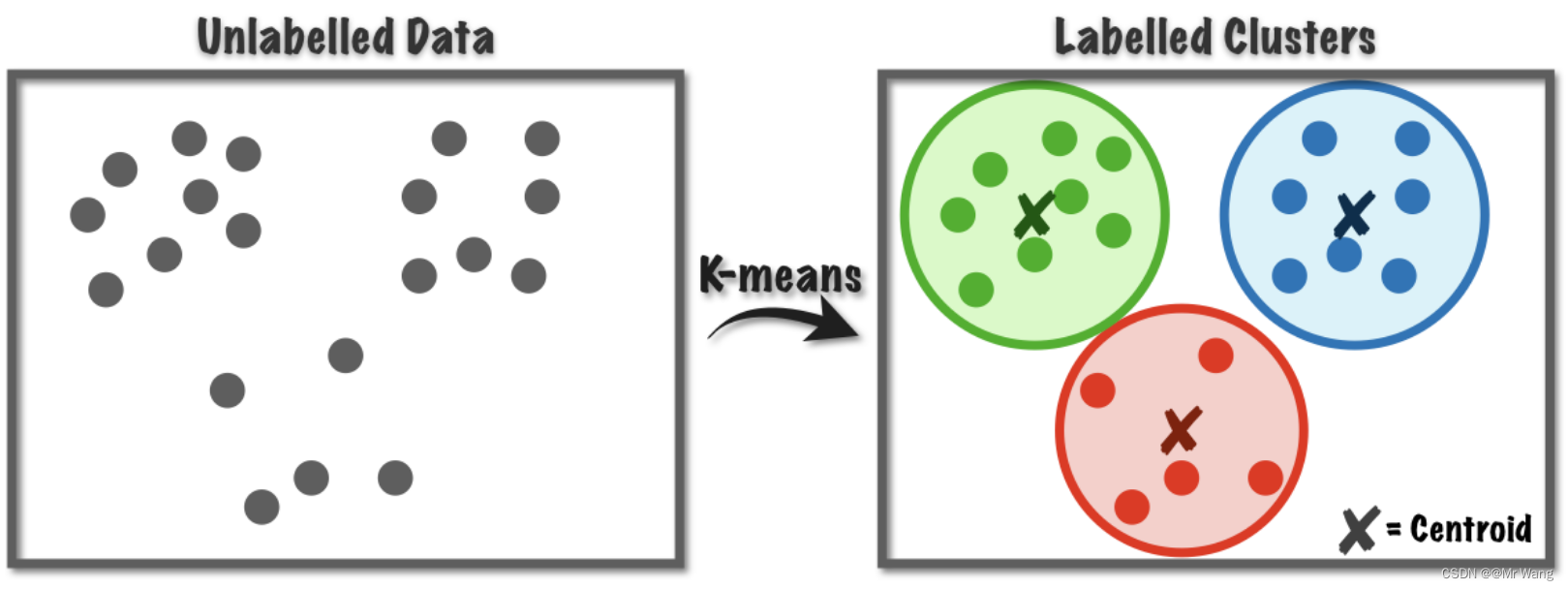
聚类算法是一种无监督学习的方法,用于将数据集中的对象按照特征的相似度或者距离进行分组,并且每个分组被称为一个簇。聚类即是让同一个簇内的样本相互之间更加相似,而不同的簇之间差异较大。
(了解)监督学习则是指模型根据已知的输入输出关系学习一个映射函数,以便于对新的数据进行预测或分类。在监督学习中,训练数据集包括带有标签的样本数据对(样本加标签)。这些标签可以是已知的正确输出(回归问题)或事先定义好的类别样本(分类问题)。
K-Means算法又称K均值算法,属于聚类算法的一种。聚类算法就是根据相似性原则,将具有较高相似度的数据对象划分至同一类簇,将具有较高相异度的数据对象划分至不同类簇,简而言之,就是把一些没有标签(label)的数据通过聚类算法打上标签分为不同的组/簇。
聚类与分类的最大区别就是在于聚类属于无监督过程(处理事务无先验知识),而分类过程为有监督过程(存在有先验知识的训练数据集)。
最优的划分其实也就是最优的中心点的位置,未来的数据求出其与不同中心点的距离实现对其的预测。
对于预测问题,大体流程如图1所示,
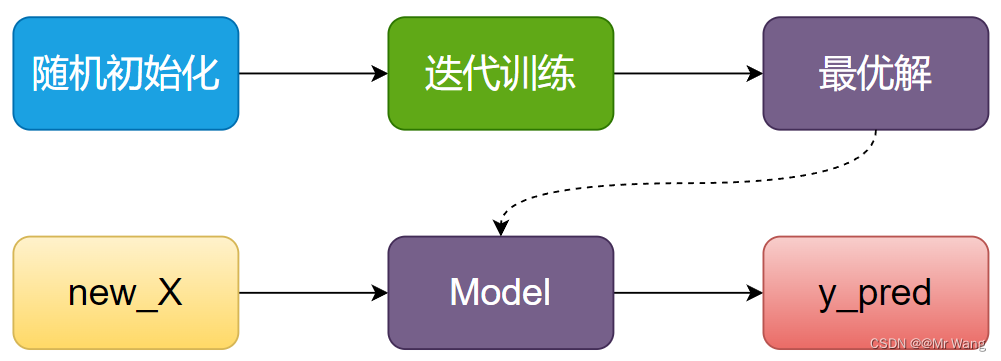
对于聚类算法,大体的流程如图2所示,
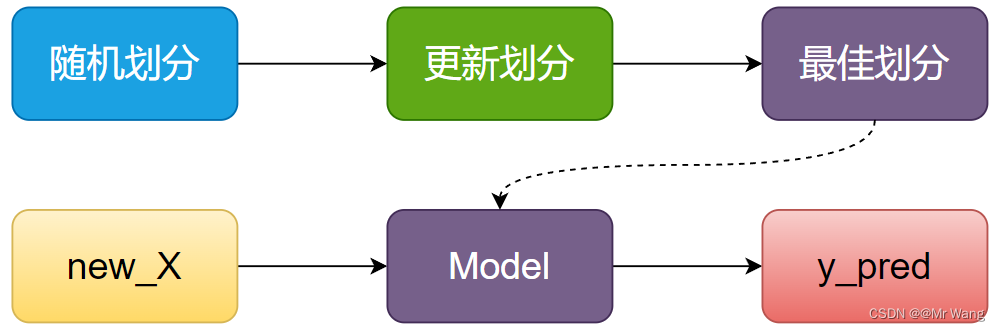
为什么要叫KMeans?因为K代表着最终的簇数量,或者说目标簇数量,需要手动设置,是一个超参数。Means是因为算法过程中需要计算平均值,下面描述一下KMeans的流程,
随机初始化簇中心点个数K
输入:样本
输出:样本所属簇
// 当样本分配到K个簇不再变化时end
While(样本的分配发生改变)for i=1,2,...,N then do样本被分配到距离其最近的中心点根据当前每个簇中的样本更新K个簇中心点:采用平均值计算end
end-
决策树
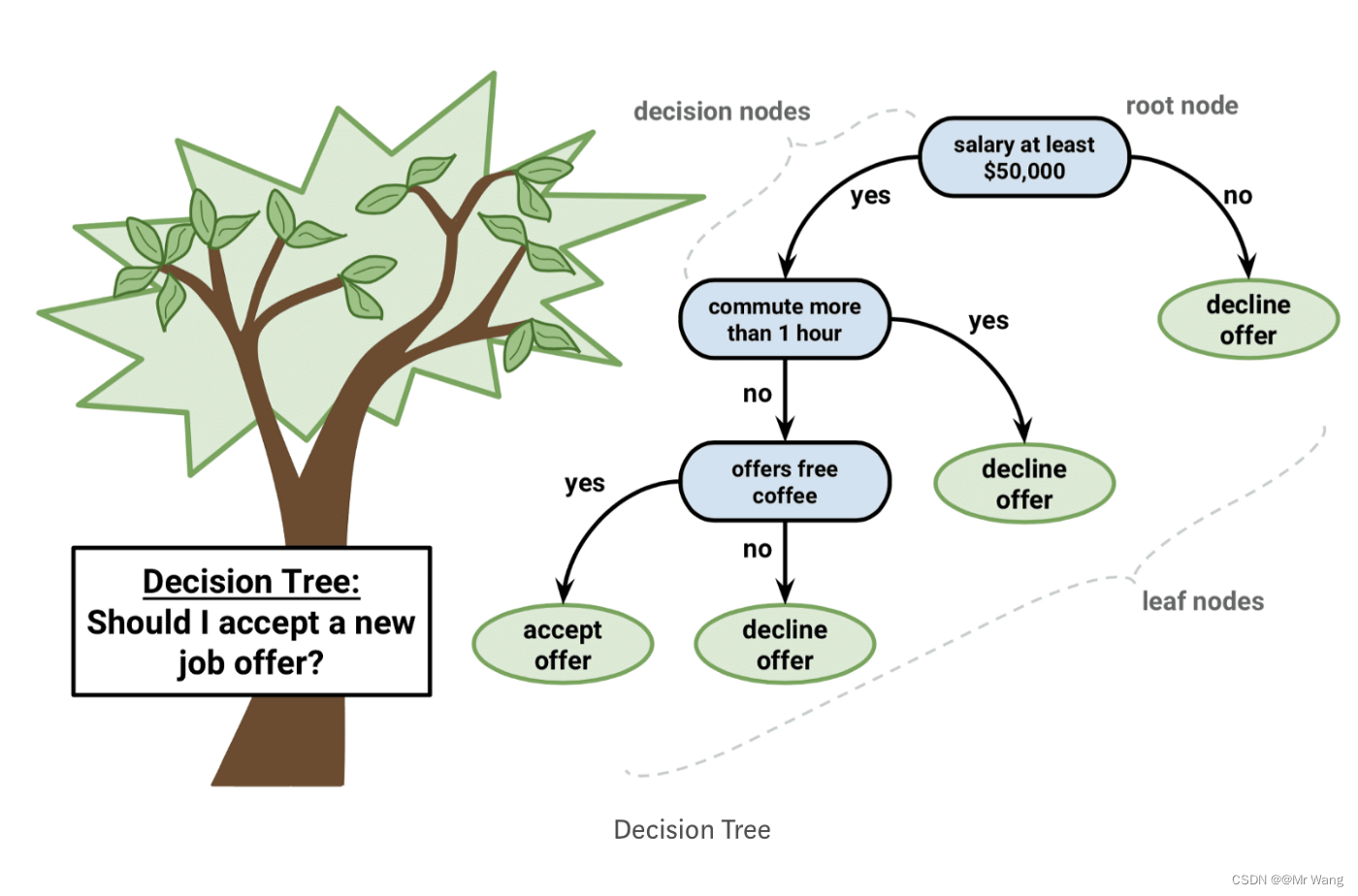
决策树是一种有监督学习,有明确的标签用于划分树的分支,符合直觉且非常直观,非叶子节点均为决策节点,每个叶子节点对应的标签即为对应的样本的预测值。需要知道回归与分类问题的区别,回归针对于连续问题,分类针对于离散问题。
特点:
决策树可以处理非线性问题,可解释性强(无seta参数),模型简单且预测效率高;不容易显示的使用函数表达,不可微XGBoost。
对于一个好的模型对一个数据集进行分类,希望得到以下两种分割方式中的哪一种?当然是分割方式2,它可以保证分割后的两个类别中,分错的类别占比很低,下面介绍一下决策树的流程。

递归解释:

上图中的b(x)=c就相当于是对应的走的子树的所在路径的值,一般为0或1,即走哪条路径哪条路径对应的值就为1。

算法描述(递归):
一共有n条样本,gt(x)表示第t个节点所对应的分值,如果节点不允许再继续分裂,即当前到达叶子节点,返回gt(x)。否则,学习分裂的条件,使得节点能不断向下分裂(就是把数据集进行划分),然后把分割后的数据(递归调用)分别重新传入DecisionTree(),构造子树,如果条件判定b(x)也不可再构造出来,构造子树结束。最后需要返回Gc(x)的加权和。
四个选择会导致决策树的形状并不唯一:分支数量、分裂的条件(用于切分数据集)、分支终止条件、基础假设(子树的叶子结点的分值如何计算,G(x))。

-
随机森林(集成学习方法)
集成学习是指通过结合多个基础学习器的预测结果提高整体的预测性能,旨在利用多个模型的优势弥补单个模型的缺点(组合多个弱学习器构建一个强学习器)。
- Bagging(自举汇聚法):通过在原始数据集上进行有放回抽样,生成多个子数据集,然后分别训练单独的基础学习器,将他们的结果进行组合。随机森林就是这种思想。
- Boosting(提升法):依次训练一系列基础学习器,每个学习器都试图修正前一个学习器的错误,最终将它们的预测结果进行加权组合。
如下图所示,从分类的角度分析(直观叙述),每个决策树都是一个分类器,对于一个输入样本,每棵树都会给出一个分类结果,而随机森林就是集成所有投票结果,根据少数服从多数的原则(使多数靠谱纠正少数不靠谱)选出最终的类别,这就是一种简单的随机森林(Bagging思想)。

有不同的树构成,每棵树的训练都相互独立,各自学习,可以实现并行,效率很高。
6、预测题案例
可以利用任意一个编程语言,或者伪代码,实现对树的定义(主要这里树的定义要根据你测量结果或者预测一棵树的样子来定义) 在图片中说明变量代表的含义,并通过代码实现对原始图片的数据分析,最终实现根据求出的关系比例来得到你预测树的结果。
import random
class Tree:def __init__(self, height, diameter, leaf_area):self.height = height # 树高self.diameter = diameter # 树径树干直径self.leaf_area = leaf_area # 叶面积def calculate_ratios(self):"""1、通过绘制样本数据固定某一属性为x轴导入matplotlib使用scatter绘制各个属性的散点图,分析为线性还是非线性关系2、或者是使用相关性分析通过结果值判断各个属性的相关性。3、假设经分析后,高与直径之间存在线性关系,叶面积与高之间存在线性关系,求解比例关系如下。"""# 数据分析部分,假设通过求高径比,叶面积与高的比,进行预测height_to_diameter_ratio = self.height/self.diameter if self.diameter != 0 else 0leaf_area_to_height_ratio = self.leaf_area/self.height if self.height != 0 else 0return height_to_diameter_ratio, leaf_area_to_height_ratiodef predict_tree(height_to_diameter_ratio, leaf_area_to_height_ratio):# 基于高径比预测直径predicted_diameter = random.uniform(0.5, 2) * height_to_diameter_ratio# 基于叶面积与树高比例预测叶面积predicted_leaf_area = random.uniform(10, 100) * leaf_area_to_height_ratioreturn predicted_diameter, predicted_leaf_area# 样本数据
trees = [Tree(10, 1, 50), # 树高 10, 树径 1, 叶面积 50Tree(12, 1.2, 60), # 树高 12, 树径 1.2, 叶面积 60Tree(9, 0.8, 40) # 树高 9, 树径 0.8, 叶面积 40
]for tree in trees:height_to_diameter_ratio, leaf_area_to_height_ratio = tree.calculate_ratios()print("树木信息:")print("树高:", tree.height)print("树径:", tree.diameter)print("叶面积:", tree.leaf_area)print("高径比:", height_to_diameter_ratio)print("叶面积与树高比例:", leaf_area_to_height_ratio)# 预测新树木的属性predicted_diameter, predicted_leaf_area = predict_tree(height_to_diameter_ratio, leaf_area_to_height_ratio)print("预测的树径:", predicted_diameter)print("预测的叶面积:", predicted_leaf_area)print("\n")class Tree:def __init__(self, height, crown_diameter, trunk_diameter):self.height = height # 树的高度self.crown_diameter = crown_diameter # 树冠直径self.trunk_diameter = trunk_diameter # 树干直径def analyze_tree_image(image):# 使用图像处理和计算机视觉算法提取树的相关参数height = measure_height(image) # 测量树的高度crown_diameter = measure_crown_diameter(image) # 测量树冠直径trunk_diameter = measure_trunk_diameter(image) # 测量树干直径return Tree(height, crown_diameter, trunk_diameter)def predict_tree(tree):# 根据测量结果和定义的树的结构,进行预测predicted_height = tree.height * scale_factor_height # 预测树的高度predicted_crown_diameter = tree.crown_diameter * scale_factor_crown_diameter # 预测树冠直径predicted_trunk_diameter = tree.trunk_diameter * scale_factor_trunk_diameter # 预测树干直径return Tree(predicted_height, predicted_crown_diameter, predicted_trunk_diameter)7、2d和3d问题
- 2d(二维):指平面上的形状或对象,具有两个坐标轴,通常为水平轴和垂直轴,在二维空间中物体只有长度和宽度两个方向的尺寸,例如平面图和照片等都是二维的。
- 3d(三维):指具有三个坐标轴的空间,通常为长度、宽度和高度三个方向的尺寸,可以从各个角度观察,例如实物体、建筑物、立体图形等。
问题描述:考虑光照,是否穿过方格,是不是球体,由3d到2d都可以应该怎么做?
- 光照影响:考虑光照时,可以使用阴影和高光来呈现3D物体在2D平面上的视觉效果。这可以通过计算每个表面的光照情况,并相应地调整其在2D表示中的亮度和颜色来实现。
- 是否穿过方格:如果物体在3D空间中与方格相交,需要确定交点并将其投影到2D平面上。这可以通过计算光线与物体的相交点,然后将其映射到2D平面上的对应位置来实现。
- 形状是否为球体:如果物体的形状为球体,则可以使用球体的投影公式将其投影到2D平面上。这可以通过计算球体与投影平面的交点来确定投影位置,并考虑球体的曲面特性来确定投影的形状和大小。
function convert3DTo2D(object3D, lightSource, grid, isSphere):result2D = empty 2D arrayfor each point in object3D:# 光照影响brightness = calculateBrightness(point, lightSource)# 是否穿过方格if intersectsGrid(point, grid):adjustPointPosition(point, grid)# 形状是否为球体if isSphere:projectedPoint = projectSphereTo2D(point)else:projectedPoint = projectPointTo2D(point)# 在2D数组中记录点的亮度result2D[projectedPoint.x][projectedPoint.y] = brightnessreturn result2D# 计算点的亮度
function calculateBrightness(point, lightSource):# 根据光照方向和点的法向量计算亮度# 这里可以使用光照模型(如Phong光照模型)进行计算# 判断点是否与方格相交
function intersectsGrid(point, grid):# 判断点是否与方格相交的逻辑# 调整点的位置,确保不穿过方格
function adjustPointPosition(point, grid):# 调整点的位置,确保不穿过方格的逻辑# 将点投影到2D平面上
function projectPointTo2D(point):# 使用投影方法将点投影到2D平面上# 将球体投影到2D平面上
function projectSphereTo2D(point):# 使用球体投影公式将点投影到2D平面上function isLightPassingThrough(grid, sphere_radius, light_position, grid_position):// 3D空间到2D投影,假设光源位于 (0, 0, 0)light_x = light_position.xlight_y = light_position.ylight_z = light_position.zgrid_x = grid_position.xgrid_y = grid_position.ygrid_z = grid_position.z// 确定光线是否经过方格的投影if (light_x == grid_x && light_y == grid_y):// 光源与方格在同一平面,无法穿过方格return falseelse if (light_x == grid_x):// 光线平行于 YZ 平面,检查 YZ 投影是否相交if (abs(light_y - grid_y) <= sphere_radius && abs(light_z - grid_z) <= sphere_radius):return trueelsereturn falseelse if (light_y == grid_y):// 光线平行于 XZ 平面,检查 XZ 投影是否相交if (abs(light_x - grid_x) <= sphere_radius && abs(light_z - grid_z) <= sphere_radius):return trueelsereturn falseelse if (light_z == grid_z):// 光线平行于 XY 平面,检查 XY 投影是否相交if (abs(light_x - grid_x) <= sphere_radius && abs(light_y - grid_y) <= sphere_radius):return trueelsereturn falseelse {// 光线不平行于任何平面,计算光线是否穿过方格// 利用球体方程 (x - light_x)^2 + (y - light_y)^2 + (z - light_z)^2 <= sphere_radius^2// 在 XY 平面上的方程a = 1b = 1c = 0d = -sphere_radius^2// 计算方格的四个顶点vertices = [(grid_x - 0.5, grid_y - 0.5),(grid_x + 0.5, grid_y - 0.5),(grid_x + 0.5, grid_y + 0.5),(grid_x - 0.5, grid_y + 0.5)]// 检查光线是否穿过方格的投影for each vertex in vertices {if (a * vertex.x + b * vertex.y + c * light_z + d >= 0) {return true}}return false}end function相关文章:

机器学习与数据挖掘知识点总结(二)分类算法
目录 1、什么是数据挖掘 2、为什么要有数据挖掘 3、数据挖掘用在分类任务中的算法 朴素贝叶斯算法 svm支持向量机算法 PCA主成分分析算法 k-means算法 决策树 1、什么是数据挖掘 数据挖掘是从大量数据中发现隐藏在其中的模式、关系和规律的过程。它利用统计学、机器学…...
MySQL数据库初体验
目录 1.数据库基本概念 1.1 数据Data 1.2 表 1.3 数据库 1.4 数据库管理系统(DBMS) 1.5 数据库系统(DBS) 2.数据库的发展 3.主流的数据库介绍 3.1 SQL Server(微软公司产品) 3.2 Oracle (甲骨文公司产品&…...

关于RDMA传输的基本流量控制
Basic flow control for RDMA transfers | The Geek in the Corner (wordpress.com) 名词解释 IB : InfiniBand的缩写,指的就是InfiniBand技术。 MAD : Management Datagram的缩写。MAD是InfiniBand架构中用于设备管理和配置的一种特殊消息…...
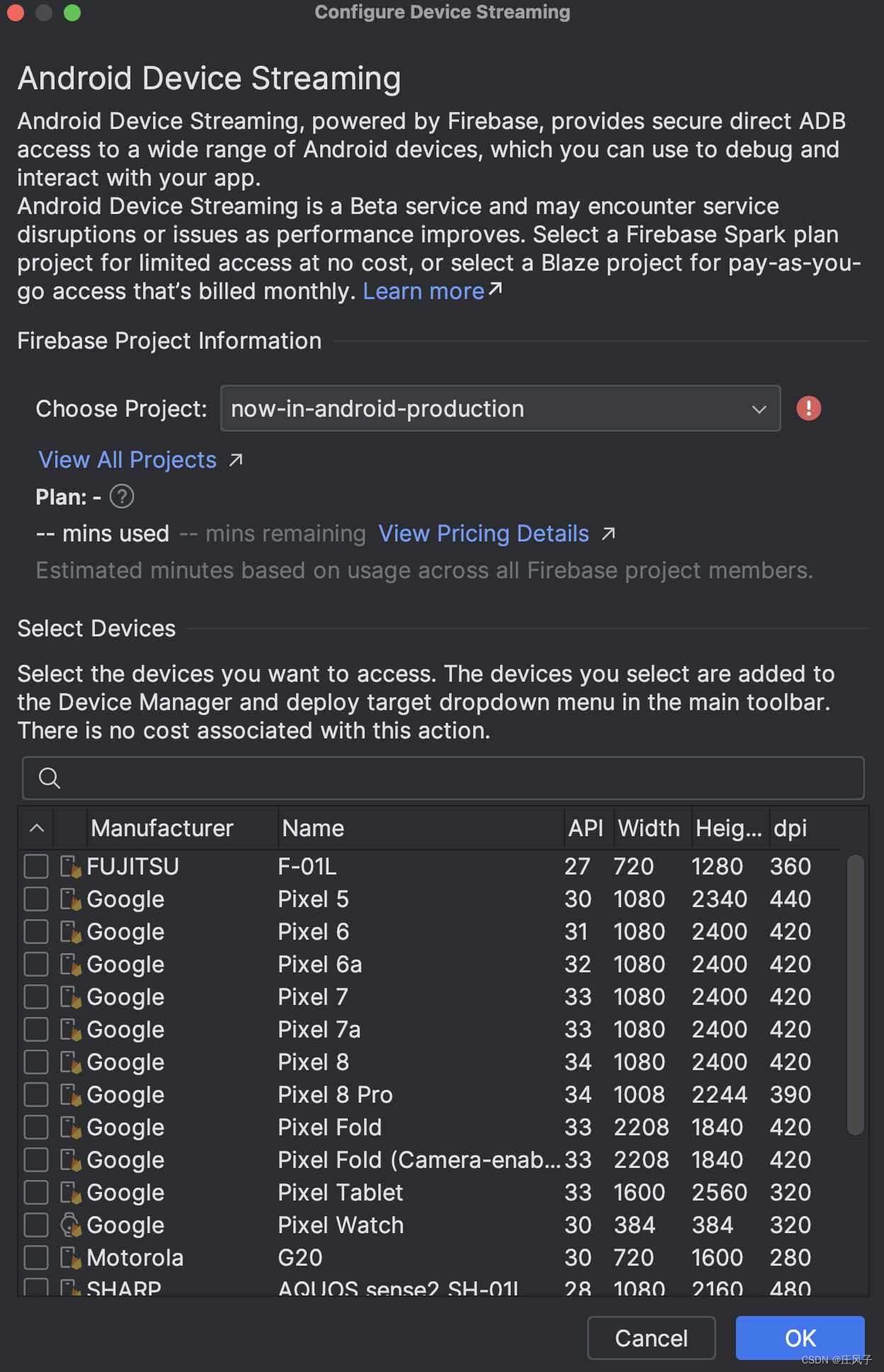
Android Studio新增功能:Device Streaming
今天将Android Studio升级到2023.3.1 Patch2。发现新增了Device Streaming功能。支持远程使用Google的物理设备调试程序。这样可以方便地在真实设备上测试自己的APP。这对于手头没有Google设备的开发者而言,确实方便很多。该功能目前处于测试阶段,在2025…...

实施ISO 26262与ISO 21434的关键要素分析
随着汽车工业的快速发展和智能化水平的不断提升,汽车的功能性和安全性成为了消费者关注的重点。为了确保车辆的安全性和可靠性,国际标准化组织(ISO)制定了一系列与汽车安全相关的标准,其中ISO 26262(道路车…...
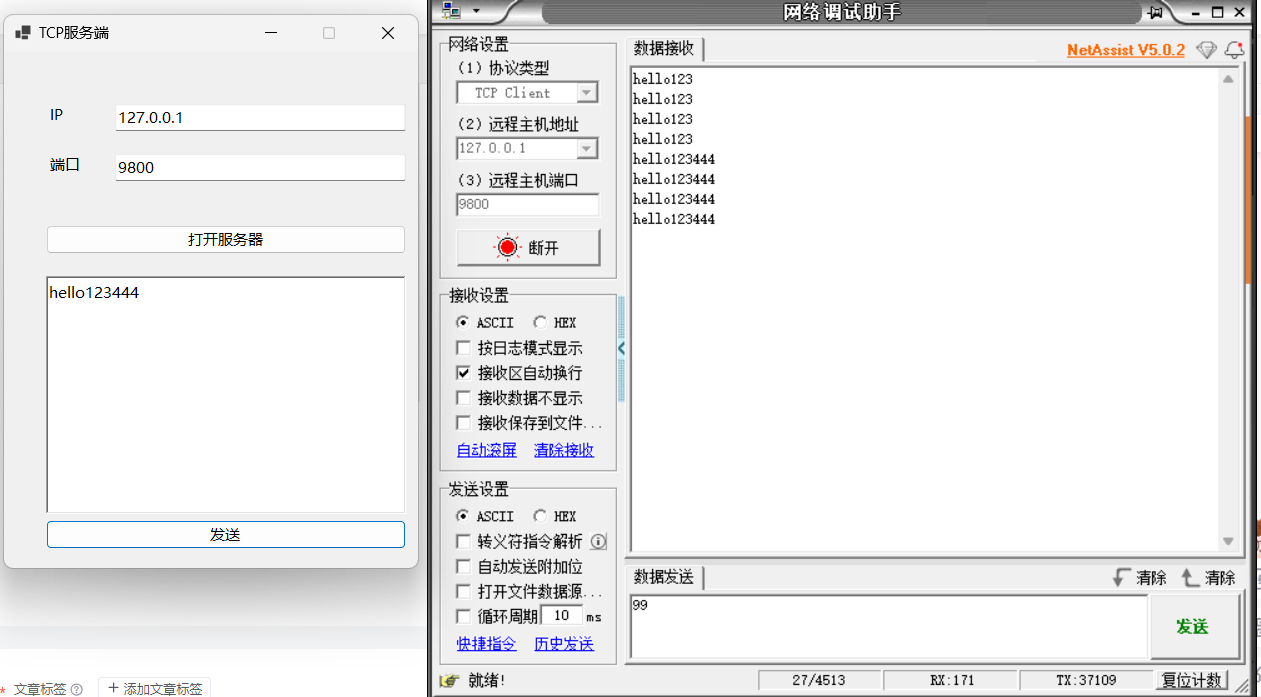
WinForm之TCP服务端
目录 一 原型 二 源码 一 原型 二 源码 using System.Net; using System.Net.Sockets; using System.Text;namespace TCP网络服务端通讯 {public partial class Form1 : Form{public Form1(){InitializeComponent();}TcpListener listener null;TcpClient handler null;Ne…...
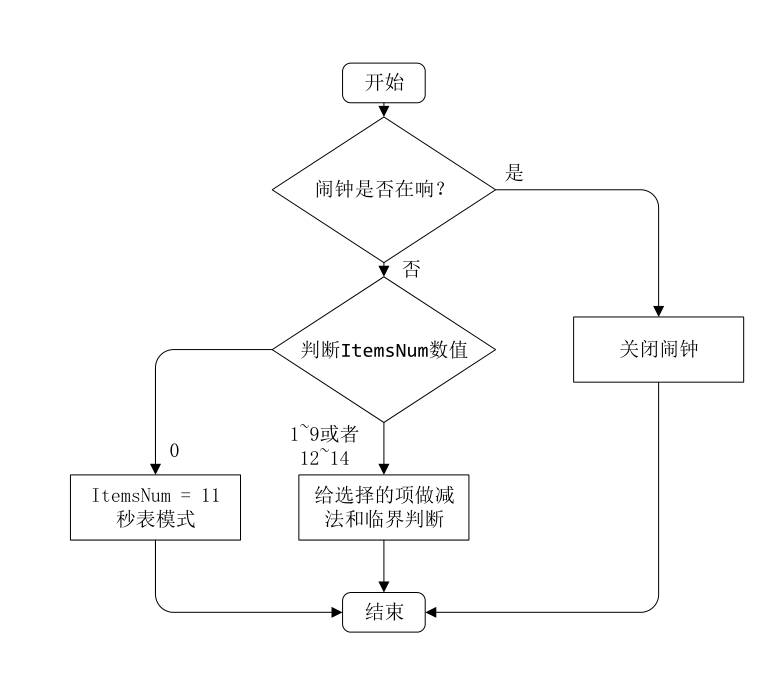
【TB作品】MSP430 G2553 单片机 口袋板 日历 时钟 闹钟 万年历 电子时钟 秒表显示
文章目录 功能介绍操作方法部分流程图代码录制了一个演示视频可以下载观看 功能介绍 时间与日期显示: 实时显示当前时间(小时、分钟、秒)和日期(年、月、日)。 闹钟功能: 设置闹钟时间(小时、分…...

推流工具OBS的下载使用
一、下载安装 OBS,windows版本官网下载地址 二、推流步骤 安装好之后,打开软件 1、右下角,打开设置 2、输入推流地址,一般为rtmp格式开头的推流地址 输入完成后,应用并确定关闭窗口 3、“来源”里面新建媒体源、新…...

【设计模式之外观模式 -- C++】
外观模式 – 统一接口,简化调用 外观模式(Facade Pattern)是一种常用的软件设计模式,它为子系统中的一组接口提供了一个统一的高层接口,使得子系统更易于使用。外观模式定义了一个高层接口,这个接口使得这…...
【课程总结】Day8(上):深度学习基本流程
前言 在上一篇课程《【课程总结】Day7:深度学习概述》中,我们了解到: 模型训练过程→本质上是固定w和b参数的过程;让模型更好→本质上就是让模型的损失值loss变小;让loss变小→本质上就是求loss函数的最小值…...

论文发表知网//新课程//简介//投稿指南
【新课程】杂志是国家新闻出版署批准,山西省新闻出版局主管,由山西三晋报刊传媒集团主办、北京师范大学科学传播与教育研究中心协办的教育类学术期刊。 【新课程】属于山西省一级、国家二级期刊,主要围绕教学改革和实践方面的问题进行探讨和研…...

全面解析AdaBoost:多分类、逻辑回归与混合分类器的实现
1. 使用 AdaBoost 完成多分类和逻辑回归问题 多分类 AdaBoost 原本是为二分类问题设计的,但可以扩展到多分类问题。常用的方法包括 One-vs-All (OVA), AdaBoost.MH (Multiclass, Multi-Label) 和 AdaBoost.MR (Multiclass Ranking)。下面对每种方法进行详细介绍。…...
:导语)
UE5实战篇二(对话系统1):导语
实现一款商业游戏中使用的对话系统插件。 虚幻商店链接: https://www.unrealengine.com/marketplace/zh-CN/product/0b84eaa9343543f58138bc4956a2fa8f 1. 内容可配置 2. 多分支对话、旁白对话、对话序列动画、文字显示及各种特效 3. 可配置文字、音效、呈现位…...

无人机的发展
朋友们,你们知道吗?无人机的发展之路可谓是科技界的一股清流,风头正劲啊!从最初简单的遥控飞机到现在各种智能功能的加持,无人机真是越来越神奇了! 首先,无人机在航拍领域大放异彩!无…...

MySQL和MariaDB的对比和选型
目录 1 基本介绍 2 功能对比 3 性能对比 4 兼容性 5 社区支持和发展 6 安全性 7 选择建议 8 结论 除去功能本身的对比,相应各位看官不一定能看出太大所以然,而且对于大部分同学来说,使用起来感觉应该差不多。 所以综合来说࿰…...

Android11 后台启动Activity
在 Android 10 (API 29) 及更高版本(包括 Android 11),系统对后台启动 Activity 施加了严格的限制。默认情况下,应用程序在后台无法启动 Activity,以提高用户体验并减少不必要的干扰。以下为解决方法。 From 7d554af386150edec1cd68f6eaf700538af4e373 Mon Sep 17 00:00:0…...
这4款国产软件,因为太良心好用,甚至被误认为是外国人开发的
说起国产软件,大家总是容易给它们打上“流氓、要钱、广告满天飞”的标签,其实,有些小众的软件超级好用,功能强大又不耍流氓,真心不该被一棍子打死。 1、sunlight studio Sunlight Studio是一个开源、免费、无广告的硬…...

【C++进阶学习】第一弹——继承(上)——探索代码复用的乐趣
前言: 在前面,我们已经将C的初阶部分全部讲完了,包括类与对象、STL、栈和队列等众多内容,今天我们就进入C进阶部分的学习,今天先来学习第一弹——继承 目录 一、什么是继承?为什么会有继承? 二…...

OpenCV单词轮廓检测
OpenCV单词轮廓检测 0. 前言1. 策略分析2. 检测字符轮廓3. 检测单词轮廓相关链接 0. 前言 在根据文档图像执行单词转录时,通常第一步是识别图像中单词的位置。我们可以使用两种不同的方法识别图像中的单词: 使用 CRAFT、EAST 等深度学习技术使用基于 O…...

主流后端开发语言对比
软件开发领域,语言本身在各自领域都有适用场景,有许多流行的编程语言可供选择,每种语言都有其独特的特点和适用场景。 Java、C、C、Go 、Python、C#、Ruby、PHP 等主流编程语言,从底层实现、效率、原理、国内外市场占有率、社区活…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...

tomcat入门
1 tomcat 是什么 apache开发的web服务器可以为java web程序提供运行环境tomcat是一款高效,稳定,易于使用的web服务器tomcathttp服务器Servlet服务器 2 tomcat 目录介绍 -bin #存放tomcat的脚本 -conf #存放tomcat的配置文件 ---catalina.policy #to…...

通过 Ansible 在 Windows 2022 上安装 IIS Web 服务器
拓扑结构 这是一个用于通过 Ansible 部署 IIS Web 服务器的实验室拓扑。 前提条件: 在被管理的节点上安装WinRm 准备一张自签名的证书 开放防火墙入站tcp 5985 5986端口 准备自签名证书 PS C:\Users\azureuser> $cert New-SelfSignedCertificate -DnsName &…...

node.js的初步学习
那什么是node.js呢? 和JavaScript又是什么关系呢? node.js 提供了 JavaScript的运行环境。当JavaScript作为后端开发语言来说, 需要在node.js的环境上进行当JavaScript作为前端开发语言来说,需要在浏览器的环境上进行 Node.js 可…...

Java多线程实现之Runnable接口深度解析
Java多线程实现之Runnable接口深度解析 一、Runnable接口概述1.1 接口定义1.2 与Thread类的关系1.3 使用Runnable接口的优势 二、Runnable接口的基本实现方式2.1 传统方式实现Runnable接口2.2 使用匿名内部类实现Runnable接口2.3 使用Lambda表达式实现Runnable接口 三、Runnabl…...

OpenGL-什么是软OpenGL/软渲染/软光栅?
软OpenGL(Software OpenGL)或者软渲染指完全通过CPU模拟实现的OpenGL渲染方式(包括几何处理、光栅化、着色等),不依赖GPU硬件加速。这种模式通常性能较低,但兼容性极强,常用于不支持硬件加速…...