全面解析AdaBoost:多分类、逻辑回归与混合分类器的实现
1. 使用 AdaBoost 完成多分类和逻辑回归问题
多分类
AdaBoost 原本是为二分类问题设计的,但可以扩展到多分类问题。常用的方法包括 One-vs-All (OVA), AdaBoost.MH (Multiclass, Multi-Label) 和 AdaBoost.MR (Multiclass Ranking)。下面对每种方法进行详细介绍。
One-vs-All (OVA)
数学原理:
-
训练过程:
- 对于每个类别 k k k ,训练一个二分类器 G k G_k Gk ,将该类别视为正类,其他类别视为负类。
- 使用二分类 AdaBoost 方法训练每个 G k G_k Gk,并获得分类器的权重 α m \alpha_m αm 。
-
预测过程:
- 对于新样本 x x x ,通过所有分类器 G k G_k Gk 进行预测,选择得分最高的分类器 G k G_k Gk 的类别作为最终预测结果:
y ^ = arg max k G k ( x ) \hat{y} = \arg\max_k G_k(x) y^=argkmaxGk(x)
- 对于新样本 x x x ,通过所有分类器 G k G_k Gk 进行预测,选择得分最高的分类器 G k G_k Gk 的类别作为最终预测结果:
通俗解释:
对于每个类别,训练一个分类器来区分该类别和其他类别。最后,通过比较所有分类器的预测得分,选择得分最高的类别作为最终分类结果。
AdaBoost.MH (Multiclass, Multi-Label)
数学原理:
-
初始化权重:
- 对于每个样本 i i i 和每个类别 k k k ,初始化权重 w ˉ i , k = 1 \bar{w}_{i,k} = 1 wˉi,k=1 。
-
迭代过程:
- 对于每一轮 m m m ,针对每个类别 k k k 和每个样本 i i i,定义权重:
w ˉ i , k = exp [ − y i , k f m − 1 ( x i , k ) ] \bar{w}_{i,k} = \exp\left[-y_{i,k} f_{m-1}(x_i, k)\right] wˉi,k=exp[−yi,kfm−1(xi,k)] - 更新分类器 G m G_m Gm 使得加权误差最小:
G m = arg min G ∑ i = 1 N ∑ k = 1 K w ˉ i , k I ( y i , k ≠ G ( x i , k ) ) G_m = \arg\min_G \sum_{i=1}^{N} \sum_{k=1}^{K} \bar{w}_{i,k} I(y_{i,k} \ne G(x_i, k)) Gm=argGmini=1∑Nk=1∑Kwˉi,kI(yi,k=G(xi,k)) - 计算误差率 ϵ m \epsilon_m ϵm 和分类器权重 α m \alpha_m αm ,更新样本权重,归一化权重,类似二分类 AdaBoost。
- 对于每一轮 m m m ,针对每个类别 k k k 和每个样本 i i i,定义权重:
-
最终分类器:
- 最终分类器 F ( x ) F(x) F(x) 是所有弱分类器的加权和:
F ( x ) = ∑ m = 1 M α m G m ( x ) F(x) = \sum_{m=1}^{M} \alpha_m G_m(x) F(x)=m=1∑MαmGm(x)
- 最终分类器 F ( x ) F(x) F(x) 是所有弱分类器的加权和:
通俗解释:
将多分类问题视为多个二分类问题,并通过调整样本权重来增强分类效果。每个类别都有独立的权重,最终通过加权求和得到最终分类结果。
AdaBoost.MR (Multiclass Ranking)
数学原理:
-
初始化权重:
- 对于每个样本 i i i 和每个类别 k k k ,初始化权重 w ˉ i , k = 1 \bar{w}_{i,k} = 1 wˉi,k=1 。
-
迭代过程:
- 在每轮迭代中,更新分类器 G m G_m Gm 使得加权误差最小,并基于对样本排序的思想选择最佳分类器:
G m = arg min G ∑ i = 1 N ∑ k = 1 K w ˉ i , k I ( y i , k ≠ G ( x i , k ) ) G_m = \arg\min_G \sum_{i=1}^{N} \sum_{k=1}^{K} \bar{w}_{i,k} I(y_{i,k} \ne G(x_i, k)) Gm=argGmini=1∑Nk=1∑Kwˉi,kI(yi,k=G(xi,k)) - 计算误差率 ϵ m \epsilon_m ϵm 和分类器权重 α m \alpha_m αm ,更新样本权重,归一化权重,类似二分类 AdaBoost。
- 在每轮迭代中,更新分类器 G m G_m Gm 使得加权误差最小,并基于对样本排序的思想选择最佳分类器:
-
最终分类器:
- 最终分类器 F ( x ) F(x) F(x) 是所有弱分类器的加权和:
F ( x ) = ∑ m = 1 M α m G m ( x ) F(x) = \sum_{m=1}^{M} \alpha_m G_m(x) F(x)=m=1∑MαmGm(x)
- 最终分类器 F ( x ) F(x) F(x) 是所有弱分类器的加权和:
通俗解释:
基于对样本的排序,将多个分类器的输出进行排序,选择得分最高的类别作为最终预测结果。
逻辑回归
将 AdaBoost 与逻辑回归结合,可以通过每轮迭代增加一个逻辑回归分类器来增强模型的能力。
数学原理:
- 初始化: 给定训练数据 ( x i , y i ) (x_i, y_i) (xi,yi),初始权重 w i = 1 N w_i = \frac{1}{N} wi=N1。
- 迭代过程:
- 对于每一轮 m m m ,训练逻辑回归模型 G m G_m Gm:
G m ( x ) = 1 1 + exp ( − β m h m ( x ) ) G_m(x) = \frac{1}{1 + \exp(-\beta_m h_m(x))} Gm(x)=1+exp(−βmhm(x))1 - 更新权重:
w ˉ i = w i exp [ − y i G m ( x i ) ] \bar{w}_{i} = w_i \exp\left[-y_i G_m(x_i)\right] wˉi=wiexp[−yiGm(xi)] - 归一化权重:
w i = w ˉ i ∑ j = 1 N w ˉ j w_i = \frac{\bar{w}_i}{\sum_{j=1}^{N} \bar{w}_j} wi=∑j=1Nwˉjwˉi
- 对于每一轮 m m m ,训练逻辑回归模型 G m G_m Gm:
通俗解释:
逻辑回归是一种用来预测二分类问题的模型。将逻辑回归与 AdaBoost 结合,可以通过逐步增加多个逻辑回归模型来提高整体的预测性能。在每轮迭代中,增加一个新的逻辑回归模型,并根据上一个模型的预测结果调整样本的权重,使得模型更关注那些被错误分类的样本。
2. 训练中选择不同的分类器
AdaBoost 是一种增强学习算法,通过组合多个弱分类器来提高分类性能。这里我们详细描述如何在 AdaBoost 中应用决策树桩、朴素贝叶斯和支持向量机(SVM)作为基础分类器,并解释其数学原理和实现方法。
1. 决策树桩
数学原理:
决策树桩是非常简单的决策树,通常只包含一个决策节点和两个叶节点。它是 AdaBoost 中常用的基础分类器。
步骤:
-
初始化权重:
- 初始化每个样本的权重为 w i = 1 N w_i = \frac{1}{N} wi=N1,其中 N N N 是样本数。
-
迭代过程:
- 对于每一轮 m m m,训练一个新的决策树桩 G m G_m Gm:
G m ( x ) = arg min G ∑ i = 1 N w i I ( y i ≠ G ( x i ) ) G_m(x) = \arg\min_{G} \sum_{i=1}^{N} w_i I(y_i \ne G(x_i)) Gm(x)=argGmini=1∑NwiI(yi=G(xi)) - 计算误差率 ϵ m \epsilon_m ϵm:
ϵ m = ∑ i = 1 N w i I ( y i ≠ G m ( x i ) ) \epsilon_m = \sum_{i=1}^{N} w_i I(y_i \ne G_m(x_i)) ϵm=i=1∑NwiI(yi=Gm(xi)) - 计算分类器的权重 α m \alpha_m αm:
α m = 1 2 ln ( 1 − ϵ m ϵ m ) \alpha_m = \frac{1}{2} \ln\left(\frac{1 - \epsilon_m}{\epsilon_m}\right) αm=21ln(ϵm1−ϵm) - 更新样本权重:
w i ← w i exp ( − α m y i G m ( x i ) ) w_i \leftarrow w_i \exp\left(-\alpha_m y_i G_m(x_i)\right) wi←wiexp(−αmyiGm(xi)) - 归一化权重:
w i ← w i ∑ j = 1 N w j w_i \leftarrow \frac{w_i}{\sum_{j=1}^{N} w_j} wi←∑j=1Nwjwi
- 对于每一轮 m m m,训练一个新的决策树桩 G m G_m Gm:
-
最终分类器:
- 最终分类器 F ( x ) F(x) F(x) 是所有弱分类器的加权和:
F ( x ) = ∑ m = 1 M α m G m ( x ) F(x) = \sum_{m=1}^{M} \alpha_m G_m(x) F(x)=m=1∑MαmGm(x)
- 最终分类器 F ( x ) F(x) F(x) 是所有弱分类器的加权和:
通俗解释:
在每一轮迭代中,选择一个简单的决策树桩作为弱分类器,然后根据该分类器的表现来调整样本的权重,使得分类错误的样本权重增加。在下一轮迭代中,新的分类器将更关注这些错误分类的样本。最终,将所有弱分类器的结果加权求和得到最终分类结果。
2. 朴素贝叶斯
数学原理:
朴素贝叶斯假设特征之间相互独立,使用贝叶斯定理计算类别的后验概率。
步骤:
-
初始化权重:
- 初始化每个样本的权重为 w i = 1 N w_i = \frac{1}{N} wi=N1,其中 N N N 是样本数。
-
迭代过程:
- 对于每一轮 m m m,训练一个新的朴素贝叶斯分类器 G m G_m Gm:
G m ( x ) = arg max y P ( y ∣ x ) = arg max y P ( x ∣ y ) P ( y ) P ( x ) G_m(x) = \arg\max_{y} P(y | x) = \arg\max_{y} \frac{P(x | y) P(y)}{P(x)} Gm(x)=argymaxP(y∣x)=argymaxP(x)P(x∣y)P(y) - 计算误差率 ϵ m \epsilon_m ϵm 和分类器权重 α m \alpha_m αm,更新样本权重,归一化权重,类似决策树桩。
- 对于每一轮 m m m,训练一个新的朴素贝叶斯分类器 G m G_m Gm:
-
最终分类器:
- 最终分类器 F ( x ) F(x) F(x) 是所有弱分类器的加权和:
F ( x ) = ∑ m = 1 M α m G m ( x ) F(x) = \sum_{m=1}^{M} \alpha_m G_m(x) F(x)=m=1∑MαmGm(x)
- 最终分类器 F ( x ) F(x) F(x) 是所有弱分类器的加权和:
通俗解释:
朴素贝叶斯假设所有特征独立,并根据训练数据计算每个类别的概率。在每一轮迭代中,使用新的朴素贝叶斯分类器进行分类,并调整样本权重,使得错误分类的样本在下一轮中更加重要。最终将所有分类器的结果加权求和得到最终分类结果。
3. 支持向量机 (SVM)
数学原理:
SVM 通过找到一个超平面来最大化类间间隔,从而实现分类。
步骤:
-
初始化权重:
- 初始化每个样本的权重为 w i = 1 N w_i = \frac{1}{N} wi=N1,其中 N N N 是样本数。
-
迭代过程:
- 对于每一轮 m m m,训练一个新的 SVM 分类器 G m G_m Gm,目标是最大化类间间隔:
min w 1 2 ∥ w ∥ 2 subject to y i ( w ⋅ x i + b ) ≥ 1 \min_w \frac{1}{2} \|w\|^2 \quad \text{subject to} \quad y_i (w \cdot x_i + b) \ge 1 wmin21∥w∥2subject toyi(w⋅xi+b)≥1 - 使用样本权重 w i w_i wi 进行加权训练,使得 SVM 更关注权重较大的样本。
- 计算误差率 ϵ m \epsilon_m ϵm 和分类器权重 α m \alpha_m αm,更新样本权重,归一化权重,类似决策树桩。
- 对于每一轮 m m m,训练一个新的 SVM 分类器 G m G_m Gm,目标是最大化类间间隔:
-
最终分类器:
- 最终分类器 F ( x ) F(x) F(x) 是所有弱分类器的加权和:
F ( x ) = ∑ m = 1 M α m G m ( x ) F(x) = \sum_{m=1}^{M} \alpha_m G_m(x) F(x)=m=1∑MαmGm(x)
- 最终分类器 F ( x ) F(x) F(x) 是所有弱分类器的加权和:
通俗解释:
SVM 寻找一个能够最大化类间间隔的超平面来进行分类。在每一轮迭代中,使用加权的样本训练新的 SVM 分类器,使得错误分类的样本在下一轮中更加重要。最终将所有分类器的结果加权求和得到最终分类结果。
结论
在 AdaBoost 中,可以选择不同的基础分类器,如决策树桩、朴素贝叶斯和 SVM。每种分类器有其独特的训练方式和优势。通过逐轮训练新的基础分类器,并根据误分类调整样本权重,AdaBoost 能够逐步增强分类性能,最终得到一个强分类器。
好的,让我们更深入地探讨在同一个训练中使用不同分类器的过程,并结合具体实例进行详细分析。
3. 在同一个训练中使用不同的分类器
在 AdaBoost 中使用不同类型的分类器,称为 混合增强学习(Hybrid Boosting) 。这种方法在某些情况下可以提高分类性能。
应用场景和必要性
-
复杂数据集:
- 对于复杂的数据集,不同的分类器可能在不同的数据子集上表现优异。混合使用不同的分类器可以综合利用各分类器的优势。
-
提高泛化能力:
- 混合分类器可以减少单一分类器的偏差和方差,从而提高模型的泛化能力。
-
适应性:
- 不同的分类器可能对不同的特征类型更敏感。通过混合分类器,可以更好地捕捉数据的不同特征。
数学原理和实现
以一个具体实例进行详细分析,假设我们要分类一个包含三类的复杂数据集,其中特征类型多样。
初始化权重
- 初始化权重:
- 对于每个样本 i i i ,初始化权重 w i = 1 N w_i = \frac{1}{N} wi=N1 ,其中 N N N 是样本总数。
迭代过程
假设我们有三个基础分类器:决策树桩(Tree Stump),朴素贝叶斯(Naive Bayes),支持向量机(SVM)。在每轮迭代中,我们选择不同的分类器来训练模型。
-
第一轮:决策树桩
- 训练决策树桩 G 1 G_1 G1 ,计算误差率 ϵ 1 \epsilon_1 ϵ1:
ϵ 1 = ∑ i = 1 N w i I ( y i ≠ G 1 ( x i ) ) \epsilon_1 = \sum_{i=1}^{N} w_i I(y_i \ne G_1(x_i)) ϵ1=i=1∑NwiI(yi=G1(xi)) - 计算分类器权重 α 1 \alpha_1 α1:
α 1 = 1 2 ln ( 1 − ϵ 1 ϵ 1 ) \alpha_1 = \frac{1}{2} \ln\left(\frac{1 - \epsilon_1}{\epsilon_1}\right) α1=21ln(ϵ11−ϵ1) - 更新样本权重:
w i ← w i exp ( − α 1 y i G 1 ( x i ) ) w_i \leftarrow w_i \exp\left(-\alpha_1 y_i G_1(x_i)\right) wi←wiexp(−α1yiG1(xi)) - 归一化权重:
w i ← w i ∑ j = 1 N w j w_i \leftarrow \frac{w_i}{\sum_{j=1}^{N} w_j} wi←∑j=1Nwjwi
- 训练决策树桩 G 1 G_1 G1 ,计算误差率 ϵ 1 \epsilon_1 ϵ1:
-
第二轮:朴素贝叶斯
- 使用更新后的样本权重,训练朴素贝叶斯分类器 G 2 G_2 G2,计算误差率 ϵ 2 \epsilon_2 ϵ2 :
ϵ 2 = ∑ i = 1 N w i I ( y i ≠ G 2 ( x i ) ) \epsilon_2 = \sum_{i=1}^{N} w_i I(y_i \ne G_2(x_i)) ϵ2=i=1∑NwiI(yi=G2(xi)) - 计算分类器权重 α 2 \alpha_2 α2:
α 2 = 1 2 ln ( 1 − ϵ 2 ϵ 2 ) \alpha_2 = \frac{1}{2} \ln\left(\frac{1 - \epsilon_2}{\epsilon_2}\right) α2=21ln(ϵ21−ϵ2) - 更新样本权重:
w i ← w i exp ( − α 2 y i G 2 ( x i ) ) w_i \leftarrow w_i \exp\left(-\alpha_2 y_i G_2(x_i)\right) wi←wiexp(−α2yiG2(xi)) - 归一化权重:
w i ← w i ∑ j = 1 N w j w_i \leftarrow \frac{w_i}{\sum_{j=1}^{N} w_j} wi←∑j=1Nwjwi
- 使用更新后的样本权重,训练朴素贝叶斯分类器 G 2 G_2 G2,计算误差率 ϵ 2 \epsilon_2 ϵ2 :
-
第三轮:支持向量机
- 使用更新后的样本权重,训练支持向量机 G 3 G_3 G3 ,计算误差率 ϵ 3 \epsilon_3 ϵ3 :
ϵ 3 = ∑ i = 1 N w i I ( y i ≠ G 3 ( x i ) ) \epsilon_3 = \sum_{i=1}^{N} w_i I(y_i \ne G_3(x_i)) ϵ3=i=1∑NwiI(yi=G3(xi)) - 计算分类器权重 α 3 \alpha_3 α3 :
α 3 = 1 2 ln ( 1 − ϵ 3 ϵ 3 ) \alpha_3 = \frac{1}{2} \ln\left(\frac{1 - \epsilon_3}{\epsilon_3}\right) α3=21ln(ϵ31−ϵ3) - 更新样本权重:
w i ← w i exp ( − α 3 y i G 3 ( x i ) ) w_i \leftarrow w_i \exp\left(-\alpha_3 y_i G_3(x_i)\right) wi←wiexp(−α3yiG3(xi)) - 归一化权重:
w i ← w i ∑ j = 1 N w j w_i \leftarrow \frac{w_i}{\sum_{j=1}^{N} w_j} wi←∑j=1Nwjwi
- 使用更新后的样本权重,训练支持向量机 G 3 G_3 G3 ,计算误差率 ϵ 3 \epsilon_3 ϵ3 :
最终分类器
最终分类器 F ( x ) F(x) F(x) 是所有弱分类器的加权和:
F ( x ) = ∑ m = 1 M α m G m ( x ) F(x) = \sum_{m=1}^{M} \alpha_m G_m(x) F(x)=m=1∑MαmGm(x)
示例分析
假设我们有一个包含 10 个样本的数据集(简化为演示),每个样本具有两个特征,目标是将这些样本分类为三类(1, 2, 3)。
初始化权重
初始化所有样本的权重 w i = 1 10 = 0.1 w_i = \frac{1}{10} = 0.1 wi=101=0.1 。
第一轮迭代:决策树桩
- 训练一个简单的决策树桩,得到分类器 G 1 G_1 G1。
- 计算分类误差率 ϵ 1 \epsilon_1 ϵ1,假设 ϵ 1 = 0.3 \epsilon_1 = 0.3 ϵ1=0.3 。
- 计算分类器权重 α 1 \alpha_1 α1:
α 1 = 1 2 ln ( 1 − 0.3 0.3 ) ≈ 0.4236 \alpha_1 = \frac{1}{2} \ln\left(\frac{1 - 0.3}{0.3}\right) \approx 0.4236 α1=21ln(0.31−0.3)≈0.4236 - 更新样本权重 w i w_i wi 并归一化。
第二轮迭代:朴素贝叶斯
- 使用更新后的样本权重,训练朴素贝叶斯分类器 G 2 G_2 G2。
- 计算分类误差率 ϵ 2 \epsilon_2 ϵ2,假设 ϵ 2 = 0.25 \epsilon_2 = 0.25 ϵ2=0.25 。
- 计算分类器权重 α 2 \alpha_2 α2 :
α 2 = 1 2 ln ( 1 − 0.25 0.25 ) ≈ 0.5493 \alpha_2 = \frac{1}{2} \ln\left(\frac{1 - 0.25}{0.25}\right) \approx 0.5493 α2=21ln(0.251−0.25)≈0.5493 - 更新样本权重 w i w_i wi 并归一化。
第三轮迭代:支持向量机
- 使用更新后的样本权重,训练支持向量机 G 3 G_3 G3。
- 计算分类误差率 ϵ 3 \epsilon_3 ϵ3,假设 ϵ 3 = 0.2 \epsilon_3 = 0.2 ϵ3=0.2 。
- 计算分类器权重 α 3 \alpha_3 α3:
α 3 = 1 2 ln ( 1 − 0.2 0.2 ) ≈ 0.6931 \alpha_3 = \frac{1}{2} \ln\left(\frac{1 - 0.2}{0.2}\right) \approx 0.6931 α3=21ln(0.21−0.2)≈0.6931 - 更新样本权重 w i w_i wi 并归一化。
最终分类器
最终分类器 F ( x ) F(x) F(x) 是所有弱分类器的加权和:
F ( x ) = 0.4236 G 1 ( x ) + 0.5493 G 2 ( x ) + 0.6931 G 3 ( x ) F(x) = 0.4236 G_1(x) + 0.5493 G_2(x) + 0.6931 G_3(x) F(x)=0.4236G1(x)+0.5493G2(x)+0.6931G3(x)
通过这种方法,我们可以综合利用不同分类器的优势,提升模型的整体性能。在每轮迭代中,选择最适合当前数据的分类器,通过加权方式得到更准确的最终分类结果。
通俗解释
在每一轮迭代中,选择一个不同的分类器来训练模型。每个分类器在其擅长的数据子集上表现良好。根据每个分类器的表现,调整样本权重,使得分类错误的样本在下一轮中更加重要。最终,将所有分类器的结果加权求和得到最终分类结果。通过混合使用不同的分类器,可以充分利用各分类器的优势,提升整体模型的性能。
结论
通过使用混合增强学习,我们可以在同一个训练中使用不同的分类器(如决策树桩、朴素贝叶斯、SVM 等),提高模型的分类性能。通过具体实例分析,我们可以看到在每一轮迭代中,选择不同的分类器并调整样本权重,从而优化最终模型。这种方法在复杂数据集和不同特征类型的情况下特别有效。
相关文章:

全面解析AdaBoost:多分类、逻辑回归与混合分类器的实现
1. 使用 AdaBoost 完成多分类和逻辑回归问题 多分类 AdaBoost 原本是为二分类问题设计的,但可以扩展到多分类问题。常用的方法包括 One-vs-All (OVA), AdaBoost.MH (Multiclass, Multi-Label) 和 AdaBoost.MR (Multiclass Ranking)。下面对每种方法进行详细介绍。…...
:导语)
UE5实战篇二(对话系统1):导语
实现一款商业游戏中使用的对话系统插件。 虚幻商店链接: https://www.unrealengine.com/marketplace/zh-CN/product/0b84eaa9343543f58138bc4956a2fa8f 1. 内容可配置 2. 多分支对话、旁白对话、对话序列动画、文字显示及各种特效 3. 可配置文字、音效、呈现位…...

无人机的发展
朋友们,你们知道吗?无人机的发展之路可谓是科技界的一股清流,风头正劲啊!从最初简单的遥控飞机到现在各种智能功能的加持,无人机真是越来越神奇了! 首先,无人机在航拍领域大放异彩!无…...

MySQL和MariaDB的对比和选型
目录 1 基本介绍 2 功能对比 3 性能对比 4 兼容性 5 社区支持和发展 6 安全性 7 选择建议 8 结论 除去功能本身的对比,相应各位看官不一定能看出太大所以然,而且对于大部分同学来说,使用起来感觉应该差不多。 所以综合来说࿰…...

Android11 后台启动Activity
在 Android 10 (API 29) 及更高版本(包括 Android 11),系统对后台启动 Activity 施加了严格的限制。默认情况下,应用程序在后台无法启动 Activity,以提高用户体验并减少不必要的干扰。以下为解决方法。 From 7d554af386150edec1cd68f6eaf700538af4e373 Mon Sep 17 00:00:0…...
这4款国产软件,因为太良心好用,甚至被误认为是外国人开发的
说起国产软件,大家总是容易给它们打上“流氓、要钱、广告满天飞”的标签,其实,有些小众的软件超级好用,功能强大又不耍流氓,真心不该被一棍子打死。 1、sunlight studio Sunlight Studio是一个开源、免费、无广告的硬…...

【C++进阶学习】第一弹——继承(上)——探索代码复用的乐趣
前言: 在前面,我们已经将C的初阶部分全部讲完了,包括类与对象、STL、栈和队列等众多内容,今天我们就进入C进阶部分的学习,今天先来学习第一弹——继承 目录 一、什么是继承?为什么会有继承? 二…...

OpenCV单词轮廓检测
OpenCV单词轮廓检测 0. 前言1. 策略分析2. 检测字符轮廓3. 检测单词轮廓相关链接 0. 前言 在根据文档图像执行单词转录时,通常第一步是识别图像中单词的位置。我们可以使用两种不同的方法识别图像中的单词: 使用 CRAFT、EAST 等深度学习技术使用基于 O…...

主流后端开发语言对比
软件开发领域,语言本身在各自领域都有适用场景,有许多流行的编程语言可供选择,每种语言都有其独特的特点和适用场景。 Java、C、C、Go 、Python、C#、Ruby、PHP 等主流编程语言,从底层实现、效率、原理、国内外市场占有率、社区活…...

Linux排查问题常用命令
查看运行内存使用情况命令: free -g(单位GB)free -m(单位MB) 查看磁盘空间使用情况命令: df -h lsof命令: 诊断网络问题和分析系统资源利用情况非常有用 - lsof -n:查看已经删除的…...

【Python/Pytorch - 网络模型】-- 手把手搭建E3D LSTM网络
文章目录 文章目录 00 写在前面01 基于Pytorch版本的E3D LSTM代码02 论文下载 00 写在前面 测试代码,比较重要,它可以大概判断tensor维度在网络传播过程中,各个维度的变化情况,方便改成适合自己的数据集。 需要github上的数据集…...

C#面:Server.UrlEncode、HttpUtility.UrlDecode的区别
C#中的Server.UrlEncode和HttpUtility.UrlDecode都是用于处理URL编码和解码的方法,它们的区别如下: Server.UrlEncode: Server.UrlEncode是一个静态方法,属于System.Web命名空间。它用于将字符串进行URL编码,将特殊字…...
50.Python-web框架-Django中引入静态的bootstrap样式
目录 Bootstrap 官网 特性 下载 在线样例 Bootstrap 入门 Bootstrap v5 中文文档 v5.3 | Bootstrap 中文网 在django中使用bootstrap 新建static\bootstrap5目录,解压后的Bootstrap文件,拷贝项目里就好。 在template文件里引用css文…...

机器学习实验----支持向量机(SVM)实现二分类
目录 一、介绍 (1)解释算法 (2)数据集解释 二、算法实现和代码介绍 1.超平面 2.分类判别模型 3.点到超平面的距离 4.margin 间隔 5.拉格朗日乘数法KKT不等式 (1)介绍 (2)对偶问题 (3)惩罚参数 (4)求解 6.核函数解决非线性问题 7.SMO (1)更新w (2)更新b 三、代…...
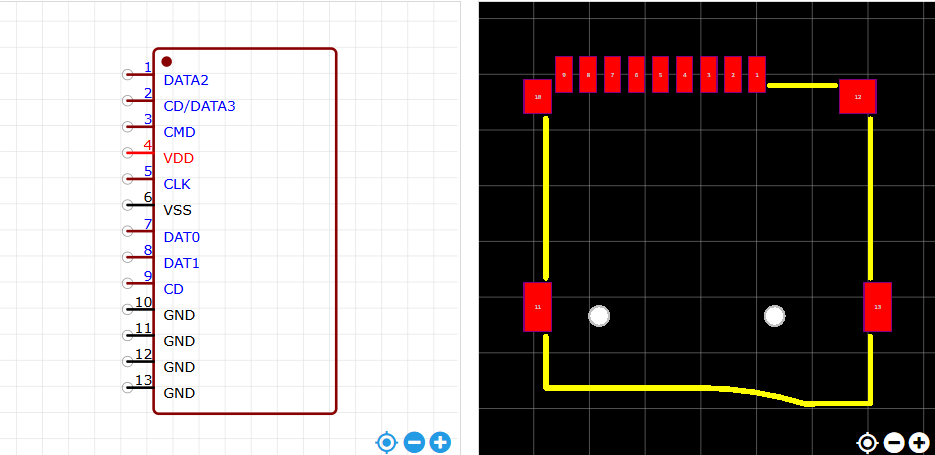
STM32自己从零开始实操05:接口电路原理图
一、TTL 转 USB 驱动电路设计 1.1指路 延续使用芯片 CH340E 。 实物图 实物图 原理图与封装图 1.2数据手册重要信息提炼 1.2.1概述 CH340 是一个 USB 总线的转接芯片,实现 USB 与串口之间的相互转化。 1.2.2特点 支持常用的 MODEM 联络信号 RTS(请…...

git子模块
1 子模块管理的关键文件和配置 在 Git 中使用子模块时,Git 会利用几个特殊的文件和配置来管理子模块。以下是涉及子模块管理的关键文件和配置: 1.1 .gitmodules 这是一个文本文件,位于 Git 仓库的根目录下。它记录了子模块的信息ÿ…...

stm32编写Modbus步骤
1. modbus协议简介: modbus协议基于rs485总线,采取一主多从的形式,主设备轮询各从设备信息,从设备不主动上报。 日常使用都是RTU模式,协议帧格式如下所示: 地址 功能码 寄存器地址 读取寄存器…...

基于 Transformer 的大语言模型
语言建模作为语言模型(LMs)的基本功能,涉及对单词序列的建模以及预测后续单词的分布。 近年来,研究人员发现,扩大语言模型的规模不仅增强了它们的语言建模能力,而且还产生了处理传统NLP任务之外更复杂任务…...

证照之星是一款很受欢迎的证件照制作软件
证照之星是一款很受欢迎的证件照制作软件,证照之星可以为用户提供“照片旋转、裁切、调色、背景处理”等功能,满足用户对证件照制作的基本需求。本站证照之星下载专题为大家提供了证照之星电脑版、安卓版、个人免费版等多个版本客户端资源,此…...
不定时更新 解决无法访问GitHub github.com 打不开 dns访问加速
1 修改hosts Windows 10为例,文件C:\Windows\System32\drivers\etc\hosts 管理员打开记事本来修改 文件-打开-“C:\Windows\System32\drivers\etc\hosts” 20.205.243.168 api.github.com 185.199.108.154 github.githubassets.com 185.199.108.133 raw.githubusercontent.…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...

【C++特殊工具与技术】优化内存分配(一):C++中的内存分配
目录 一、C 内存的基本概念 1.1 内存的物理与逻辑结构 1.2 C 程序的内存区域划分 二、栈内存分配 2.1 栈内存的特点 2.2 栈内存分配示例 三、堆内存分配 3.1 new和delete操作符 4.2 内存泄漏与悬空指针问题 4.3 new和delete的重载 四、智能指针…...

Golang——6、指针和结构体
指针和结构体 1、指针1.1、指针地址和指针类型1.2、指针取值1.3、new和make 2、结构体2.1、type关键字的使用2.2、结构体的定义和初始化2.3、结构体方法和接收者2.4、给任意类型添加方法2.5、结构体的匿名字段2.6、嵌套结构体2.7、嵌套匿名结构体2.8、结构体的继承 3、结构体与…...

Linux中《基础IO》详细介绍
目录 理解"文件"狭义理解广义理解文件操作的归类认知系统角度文件类别 回顾C文件接口打开文件写文件读文件稍作修改,实现简单cat命令 输出信息到显示器,你有哪些方法stdin & stdout & stderr打开文件的方式 系统⽂件I/O⼀种传递标志位…...

保姆级【快数学会Android端“动画“】+ 实现补间动画和逐帧动画!!!
目录 补间动画 1.创建资源文件夹 2.设置文件夹类型 3.创建.xml文件 4.样式设计 5.动画设置 6.动画的实现 内容拓展 7.在原基础上继续添加.xml文件 8.xml代码编写 (1)rotate_anim (2)scale_anim (3)translate_anim 9.MainActivity.java代码汇总 10.效果展示 逐帧…...

前端调试HTTP状态码
1xx(信息类状态码) 这类状态码表示临时响应,需要客户端继续处理请求。 100 Continue 服务器已收到请求的初始部分,客户端应继续发送剩余部分。 2xx(成功类状态码) 表示请求已成功被服务器接收、理解并处…...
