DP算法:动态规划算法
步骤
(1)确定初始状态
(2)确定转移矩阵,得到每个阶段的状态,由上一阶段推到出来
(3)确定边界条件。
例题
蓝桥杯——印章(python实现)

使用dp记录状态,dp[i][j]表示买i张印章,凑齐j种印章的概率
i表示买的印章数,j表示凑齐的印章种数
情况一:如果i<j,不可能凑齐印章,概率为0
情况二:如果j=1,dp[i][1] = n*((1/n)**i),凑齐一种印章,所有i个印章为一个种类,这一个种类有n种情况可选
情况三:凑齐j种印章。前面买了i-1个印章。可能前面i-1步凑够了j种印章,那么只用从j种里随意选出来一个dp[i-1][j]*j*p;可能前面i-1步凑够了j-1种印章,那么从剩下的n-j+1种里选出来一个dp[i-1][j-1]*(n-j+1)*p,因此为dp[i][j] = dp[i-1][j]*j*p+dp[i-1][j-1]*(n-j+1)*p
strs = input().strip().split()
n = int(strs[0])
m = int(strs[1])# 使用dp记录状态,dp[i][j]表示买i张印章,凑齐j种印章的概率
dp = [[0]*(n+1) for _ in range(m+1)]p = 1.0/nfor i in range(1,m+1):for j in range(1,n+1):# 如果i<j,不可能凑齐印章if i<j:dp[i][j] = 0# 如果凑齐一种印章elif j==1:dp[i][1] = n*(p**i)# 凑齐j种印章:可能前面i-1步凑够了j种印章,那么只用从j种里随意选出来一个;# 可能前面i-1步凑够了j-1种印章,那么从剩下的n-j+1种里选出来一个else:dp[i][j] = dp[i-1][j]*j*p+dp[i-1][j-1]*(n-j+1)*p
print('%.4f'%(dp[m][n]))
相关文章:

DP算法:动态规划算法
步骤(1)确定初始状态(2)确定转移矩阵,得到每个阶段的状态,由上一阶段推到出来(3)确定边界条件。例题蓝桥杯——印章(python实现)使用dp记录状态,d…...
一三四——一六七
一三四、JavaScript——_DOM简介 MDNq前端参考文档:DOM 概述 - Web API 接口参考 | MDN (mozilla.org) 一三五、JavaScript——HelloWorld <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta h…...

day29_JS
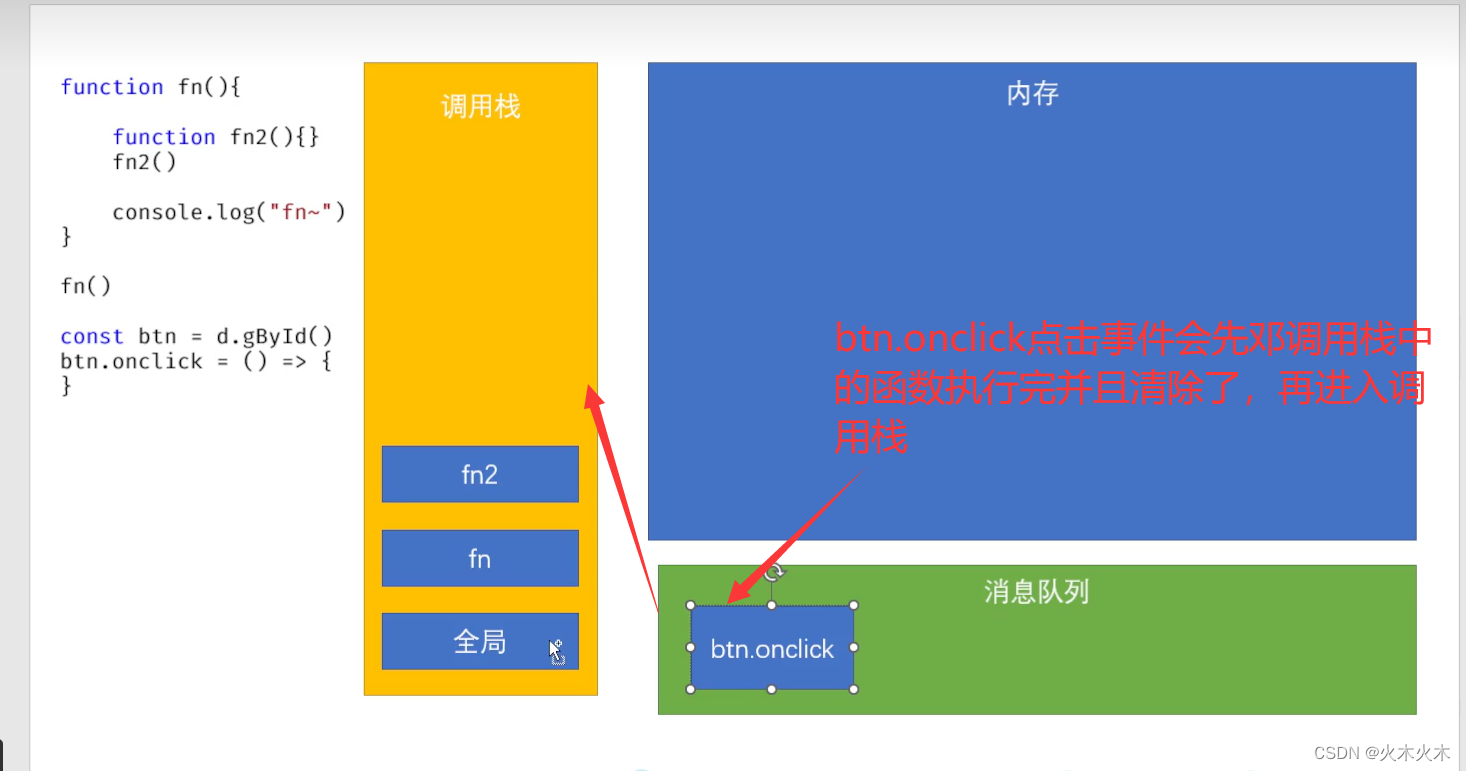
今日内容 上课同步视频:CuteN饕餮的个人空间_哔哩哔哩_bilibili 同步笔记沐沐霸的博客_CSDN博客-Java2301 零、 复习昨日 一、事件 二、DOM操作 三、案例 零、 复习昨日 js 脚本语言,弱类型 引入方案: 3种 js的内容: 语法dombom 语法 变量 var 数据类型 引用类型 - 对象,J…...
【HTTP协议与Web服务器】
HTTP协议与Web服务器浏览器与服务器通信过程HTTP的请求报头HTTP请求报头结构HTTP的请求方法HTTP应答报头HTTP应答报头结构应答状态web服务器的c语言实现浏览器与服务器通信过程 浏览器与Web服务器再应用层通信使用的是HTTP协议,而HTTP协议在传输层使用的是TCP协议。…...
Idea+maven+spring-cloud项目搭建系列--12 整合grpc
前言: grpc 是geogle 开源的rpc 通信框架,通过定义proto生成通信存根,像本地调用服务一样,进行远程服务的调用; 1 消费端服务提供: 1.1 引入grpc 和 protobuf <!-- RPC --> <!-- RPC 服务调用 …...
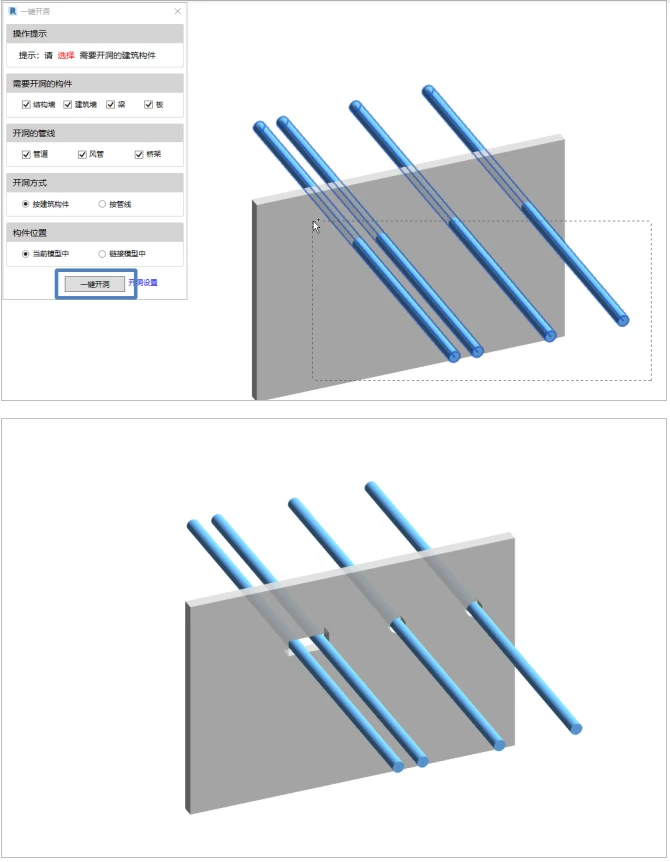
Revit开洞问题:结构专业开洞口剖面显示及一键开洞
一、Revit中关于结构专业开洞口剖面显示问题 Revit作业的时候,我们不仅只为了一个最后的三维立体模型,我们需要的是一个符合国家以及本院制图标准的一个出图样式,这时候就会出现各种各样的显示问题,本期就一个结构专业开洞显示问题,跟大家一起…...
)
0107连通分量-无向图-数据结构和算法(Java)
文章目录1 API2 代码实现和分析测试后记1 API 深度优先搜索下一个直接应用就是找出一幅图中的连通分量,定义如下API。 public class CCCC(Graph g)预处理构造函数booleanconnected(int v, int w)v和w连通吗intcount()连通分量数intid(int v)v所在的连通分量标识符(0~count()-…...
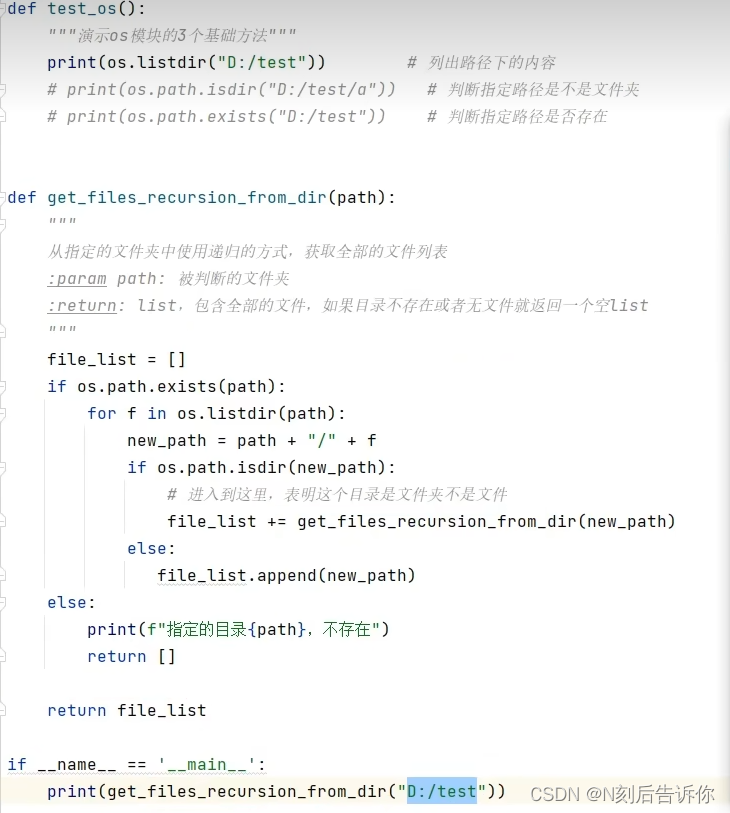
[学习笔记]黑马程序员python教程
文章目录思维导图Python基础知识图谱面向对象SQL入门和实战Python高阶技巧第一阶段第九章:Python异常、模块与包1.9.1异常的捕获1.9.1.1 为什么要捕获异常1.9.1.2 捕获常规的异常1.9.1.3 捕获指定的异常1.9.1.4 捕获多个异常1.9.1.5 捕获全部异常1.9.1.6 异常的else…...

如何配置用于构建 FastReport Online Designer 的 API ?
FastReport Online Designer 是一个跨平台的报表设计器,允许通过任何平台的移动设备创建和编辑报表。今天我们就一起来看看在2023版中新增和改进的功能有哪些,点击下方可以获取最新版免费试用哦! FastReport Onlin Designe最新版试用https:/…...
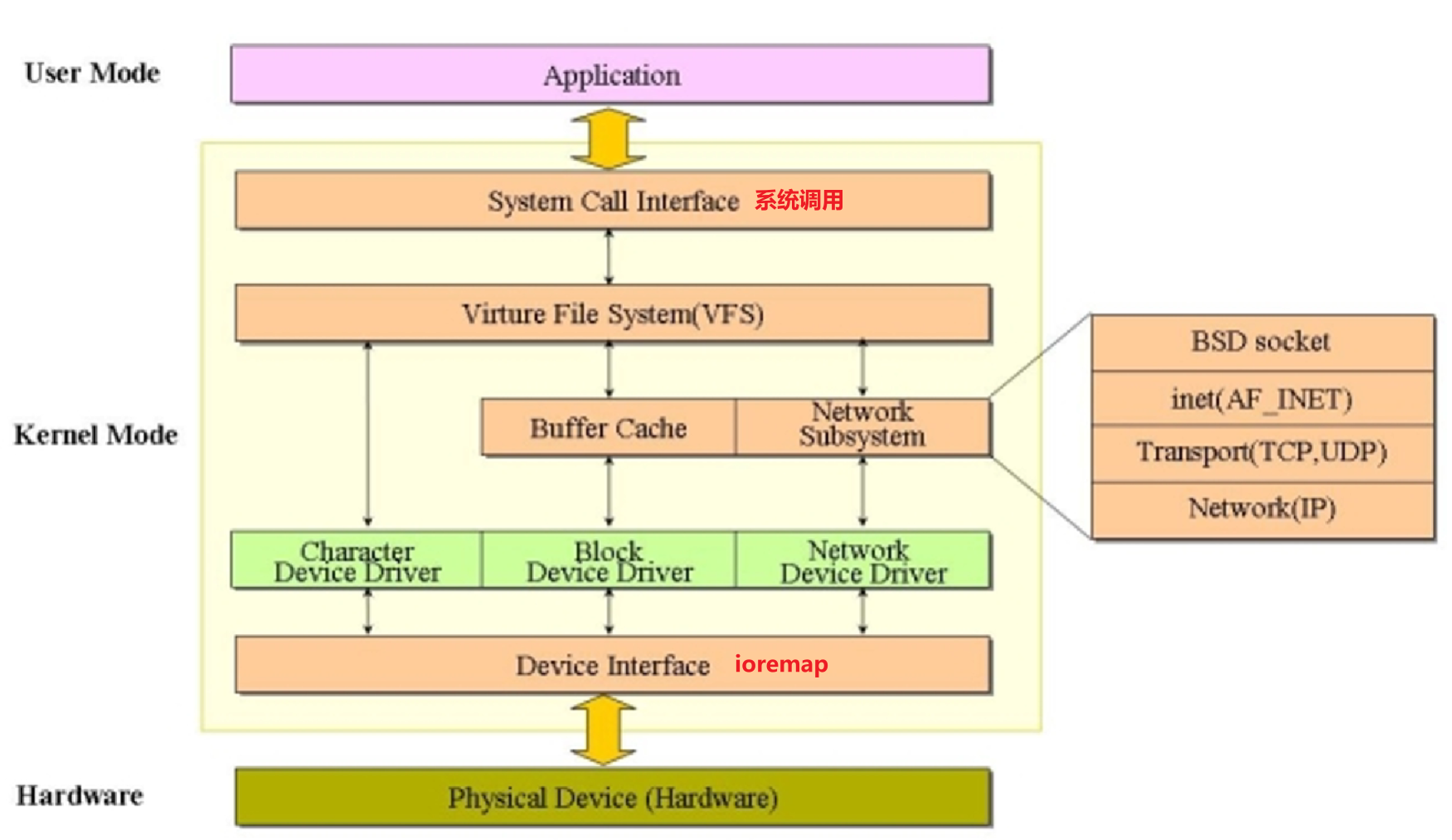
【嵌入式Linux内核驱动】02_字符设备驱动
字符设备驱动 〇、基本知识 设备驱动分类 (按共性分类方便管理) 1.字符设备驱动 字符设备指那些必须按字节流传输,以串行顺序依次进行访问的设备。它们是我们日常最常见的驱动了,像鼠标、键盘、打印机、触摸屏,还有…...

【零散整理】
1-1 git查看代码的项目总行数 git log --prettytformat: --numstat | awk ‘{ add $1; subs $2; loc $1 - $2 } END { printf “added lines: %s, removed lines: %s, total lines: %s\n”, add, subs, loc }’ - 1-2 cookie const cookies document.cookie.split(; )for…...
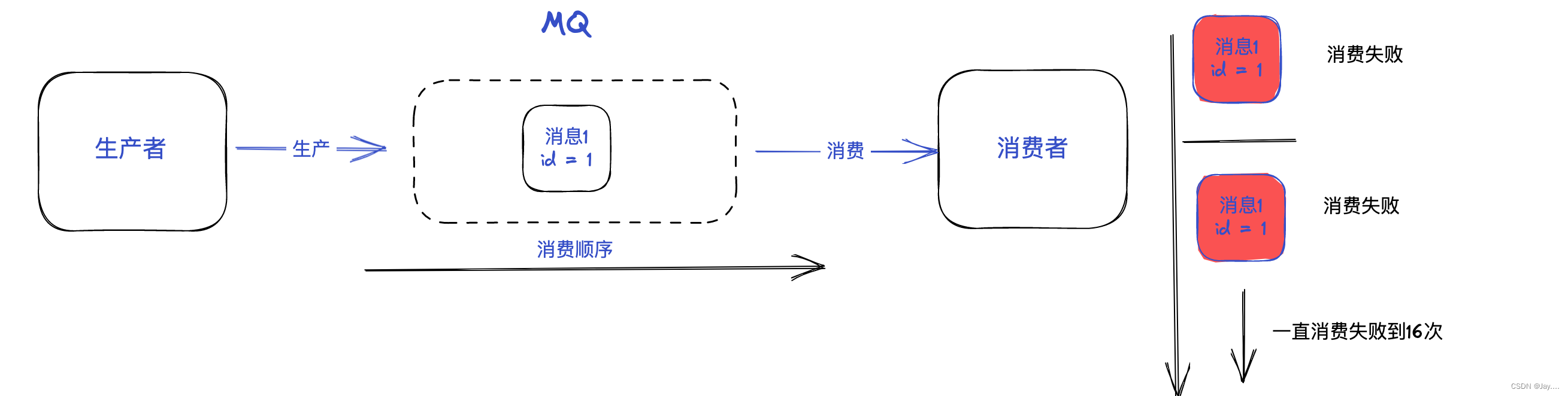
RocketMQ重复消费的症状以及解决方案
RocketMQ重复消费的症状以及解决方案 生产消息时重复 症状 当一条消息已被成功发送到 消费者 并完成持久化,此时出现了网络闪断或者客户端宕机,导致服务端对客户端应答失败。 如果此时 生产者 意识到消息发送失败并尝试再次发送消息,消费者…...
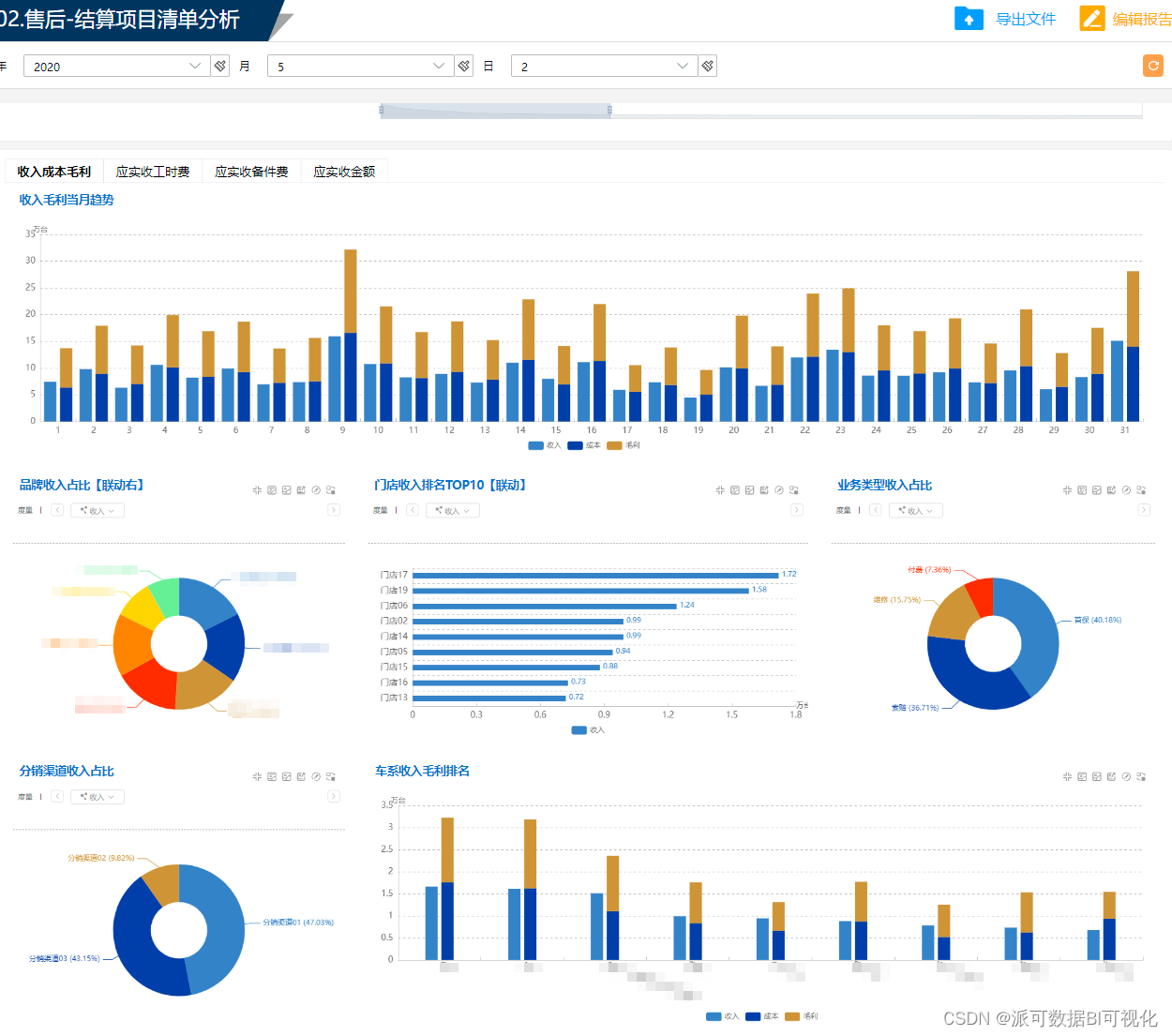
数字化时代,企业的商业模式建设
随着新一代信息化、数字化技术的应用,众多领域通过科技革命和产业革命实现了深度化的数字改造,进入到以数据为核心驱动力的,全新的数据处理时代,并通过业务系统、商业智能BI等数字化技术和应用实现了数据价值,从数字经…...
项目实战典型案例23——-注册上nacos上的部分服务总是出现频繁掉线的情况
注册上nacos上的部分服务总是出现频繁掉线的情况一:背景介绍二:思路&方案解决问题过程涉及到的知识nacos服务注册和服务发现一:背景介绍 spring cloud项目通过nacos作为服务中心和配置中心,出现的问题是其中几个服务总是出现…...
玩转金山文档 3分钟让你的文档智能化
在上个月底,我们给大家推荐了金山轻维表的几个使用场景,社群中不少用户反响很好,对其中一些场景的解决方案十分感兴趣。但也有一些人表示,有些场景不知道如何实现,希望我们能提供模版/教程。这次我们将做一期热门模板盘…...

安装了nodejs怎么安装nvm
第一步,从控制面板卸载已经安装的node 第二步,删除C盘program开头文件夹下的node文件 第三步,去C/user/用户名 文件夹下,删除.npmrc文件 第四步,打开隐藏文件,第三步文件夹下有一个Appdata文件ÿ…...

java安全编码规范考试
java安全编码规范考试 整理不易,收点币!! 安全编码规范考试.md 下面对zip文件的安全解压缩描述,错误的是 A.zip文件解压时,可以使用entry.getSize()对解压缩文件进行文件大小判断 B.zip文件解压时&…...

表格检测识别技术的发展历程
近年来,随着计算机技术的飞速发展,越来越多的研究者开始关注表格检测识别技术。表格检测识别技术是一种利用计算机自动处理表格的技术,它可以实现从文本中检测出表格,并进行识别和提取。这种技术有助于提高文本处理的效率…...
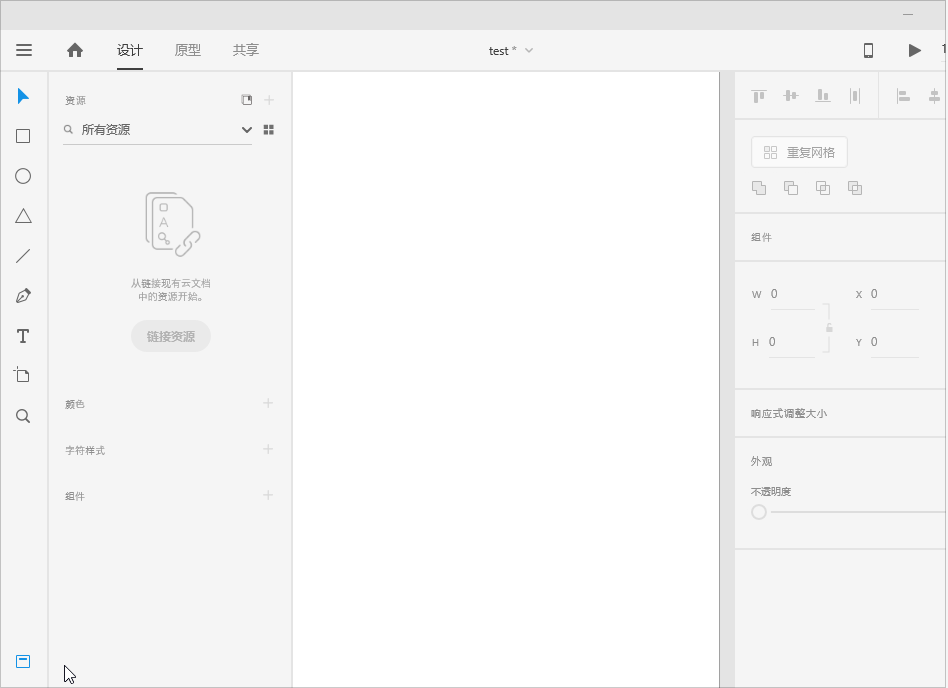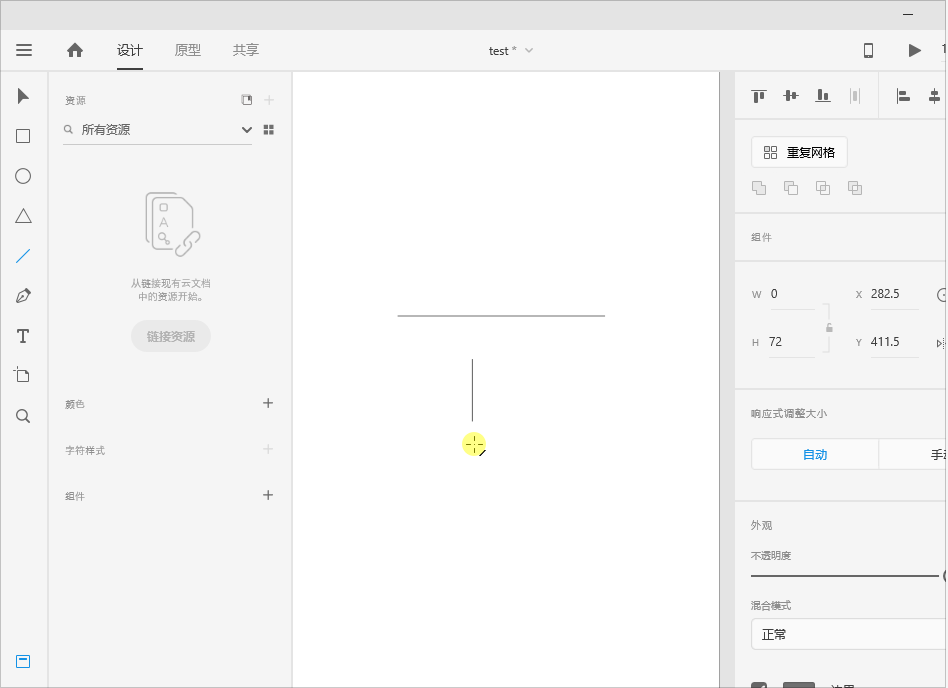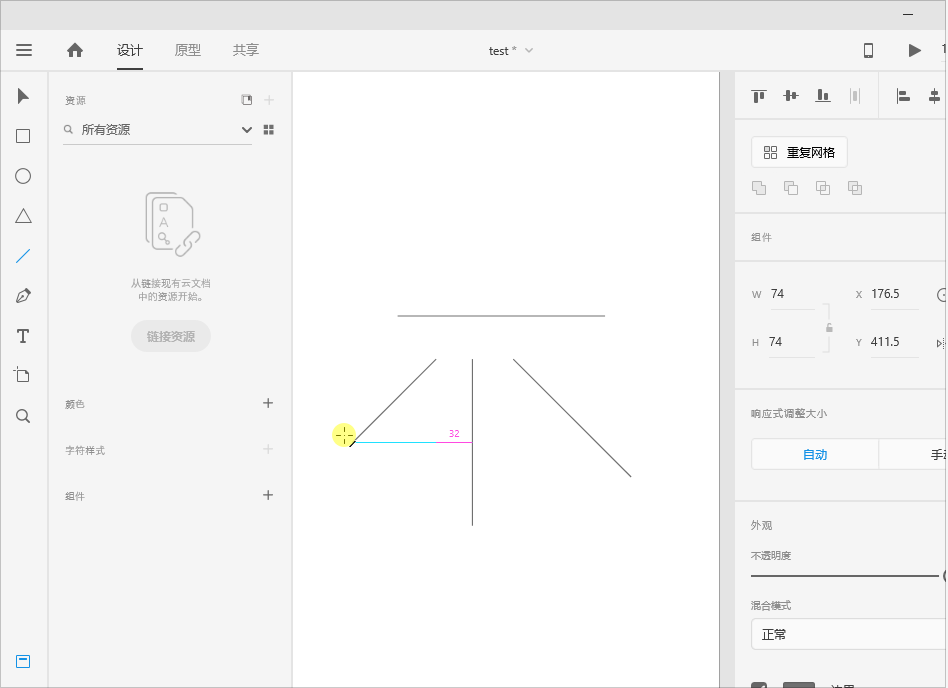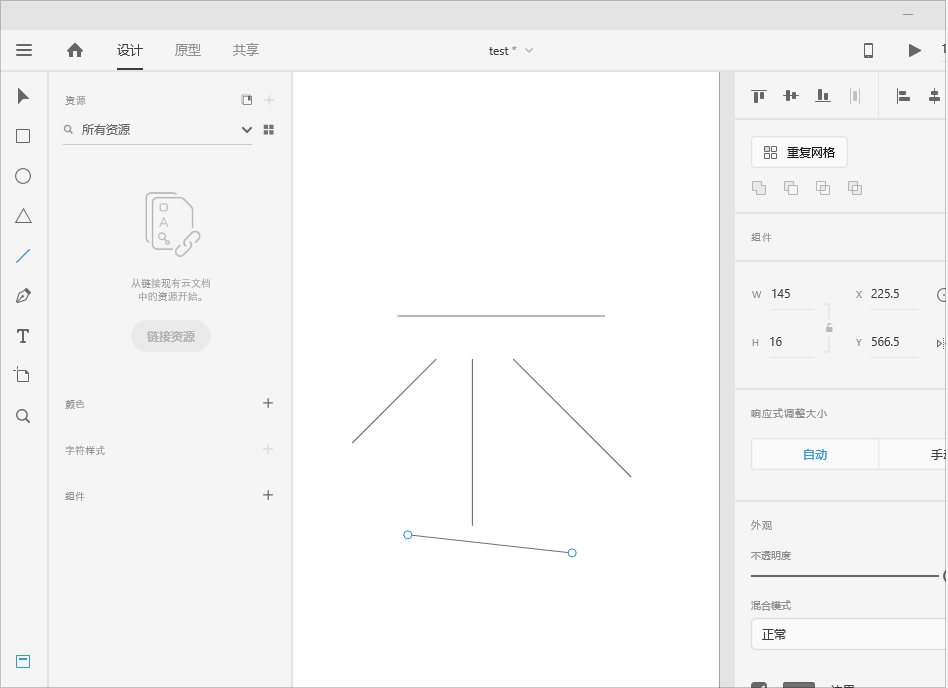
设计UI - Adobe xd对象介绍
矩形工具 新建矩形 操作步骤:选择矩形工具,快捷键R,鼠标在画板上拖出矩形即可。 拖动定界框周围圆形手柄,可快速调整矩形大小,也可以输入宽和高的参数对矩形大小进行改变。 移动矩形 操作步骤:选择选择工具…...

优思学院|精益生产中的“单件流”真的能够做到吗?
精益生产中提到的“一个流”(One Piece Flow)是一种生产方式,它的核心理念是通过合理配置作业场地、人员和设备,使产品从投入到成品产出的整个制造加工过程中始终处于不停滞、不堆积、不超越,按节拍一个一个地流动。 …...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...

Kafka主题运维全指南:从基础配置到故障处理
#作者:张桐瑞 文章目录 主题日常管理1. 修改主题分区。2. 修改主题级别参数。3. 变更副本数。4. 修改主题限速。5.主题分区迁移。6. 常见主题错误处理常见错误1:主题删除失败。常见错误2:__consumer_offsets占用太多的磁盘。 主题日常管理 …...

提升移动端网页调试效率:WebDebugX 与常见工具组合实践
在日常移动端开发中,网页调试始终是一个高频但又极具挑战的环节。尤其在面对 iOS 与 Android 的混合技术栈、各种设备差异化行为时,开发者迫切需要一套高效、可靠且跨平台的调试方案。过去,我们或多或少使用过 Chrome DevTools、Remote Debug…...

FFmpeg avformat_open_input函数分析
函数内部的总体流程如下: avformat_open_input 精简后的代码如下: int avformat_open_input(AVFormatContext **ps, const char *filename,ff_const59 AVInputFormat *fmt, AVDictionary **options) {AVFormatContext *s *ps;int i, ret 0;AVDictio…...
