四叉树和KD树
1. 简介
四叉树和KD树都是用于空间数据索引和检索的树状数据结构。它们通过将空间递归地划分为更小的区域,并存储每个区域内的点,来实现快速搜索和范围查询。
2. 四叉树
2.1 定义
四叉树是一种树状数据结构,它将二维空间递归地划分为四个相等的子区域,直到每个子区域只包含一个点或为空。每个节点代表一个矩形区域,并存储该区域内的所有点。
2.2 构建
构建四叉树的过程如下:
- 将整个空间划分为四个相等的子区域。
- 将每个点分配到相应的子区域。
- 递归地对每个子区域进行步骤 1 和 2,直到每个子区域只包含一个点或为空。
2.3 搜索
搜索四叉树的过程如下:
- 从根节点开始,检查当前节点的区域是否包含目标点。
- 如果包含,则递归地搜索该节点的四个子节点。
- 如果不包含,则搜索失败。
2.4 范围查询
范围查询是指查找所有位于给定矩形区域内的点。搜索过程与搜索单个点类似,但需要遍历所有与查询区域相交的节点。
2.5 Kotlin 代码演示
data class Point(val x: Double, val y: Double)data class Rectangle(val x: Double, val y: Double, val width: Double, val height: Double) {fun contains(point: Point): Boolean {return point.x >= x && point.x <= x + width && point.y >= y && point.y <= y + height}fun intersects(other: Rectangle): Boolean {return !(other.x + other.width < x ||other.x > x + width ||other.y + other.height < y ||other.y > y + height)}
}class QuadTree(val boundary: Rectangle, val capacity: Int = 1) {private var points: MutableList<Point> = mutableListOf()private var children: Array<QuadTree?> = arrayOfNulls(4)fun insert(point: Point): Boolean {if (!boundary.contains(point)) {return false}if (points.size < capacity) {points.add(point)return true}if (children[0] == null) {subdivide()}for (i in 0..3) {if (children[i]!!.insert(point)) {return true}}return false}private fun subdivide() {val xMid = boundary.x + boundary.width / 2val yMid = boundary.y + boundary.height / 2children[0] = QuadTree(Rectangle(boundary.x, boundary.y, xMid, yMid), capacity)children[1] = QuadTree(Rectangle(xMid, boundary.y, boundary.x + boundary.width, yMid), capacity)children[2] = QuadTree(Rectangle(boundary.x, yMid, xMid, boundary.y + boundary.height), capacity)children[3] = QuadTree(Rectangle(xMid, yMid, boundary.x + boundary.width, boundary.y + boundary.height), capacity)for (point in points) {for (i in 0..3) {if (children[i]!!.insert(point)) {break}}}points.clear()}fun query(range: Rectangle): List<Point> {val foundPoints = mutableListOf<Point>()if (!boundary.intersects(range)) {return foundPoints}for (point in points) {if (range.contains(point)) {foundPoints.add(point)}}if (children[0] != null) {for (child in children) {if (child != null) {foundPoints.addAll(child.query(range))}}}return foundPoints}
}fun main() {val boundary = Rectangle(0.0, 0.0, 10.0, 10.0)val quadTree = QuadTree(boundary, 4)val points = listOf(Point(1.0, 1.0),Point(2.0, 2.0),Point(3.0, 3.0),Point(4.0, 4.0),Point(5.0, 5.0),Point(6.0, 6.0),Point(7.0, 7.0),Point(8.0, 8.0),Point(9.0, 9.0))for (point in points) {quadTree.insert(point)}val queryRange = Rectangle(0.0, 0.0, 5.6, 4.4)val foundPoints = quadTree.query(queryRange)println("Points in range:")for (point in foundPoints) {println("(${point.x}, ${point.y})")}
}3. KD树
3.1 定义
KD树是一种树状数据结构,它将多维空间递归地划分为两个子空间,每个子空间由一个超平面分割。每个节点代表一个超矩形区域,并存储该区域内的所有点。
3.2 构建
构建KD树的过程如下:
- 选择一个维度作为分割维度,并找到该维度上的中位数。
- 使用中位数将空间划分为两个子空间。
- 递归地对每个子空间进行步骤 1 和 2,直到每个子空间只包含一个点或为空。
3.3 搜索
搜索KD树的过程如下:
- 从根节点开始,检查当前节点的区域是否包含目标点。
- 如果包含,则根据目标点的坐标选择相应的子节点进行递归搜索。
- 如果不包含,则搜索失败。
3.4 范围查询
范围查询是指查找所有位于给定超矩形区域内的点。搜索过程与搜索单个点类似,但需要遍历所有与查询区域相交的节点。
3.5 Kotlin 代码演示
// Define the Point class
internal class Point(var x: Double, var y: Double) {override fun toString(): String {return "($x, $y)"}
}// Define the k-d tree node class
internal class KDNode(var point: Point) {var left: KDNode? = nullvar right: KDNode? = null
}// Define the k-d tree class
internal class KDTree(points: List<Point>) {private val root: KDNode?init {this.root = buildTree(points, 0)}private fun buildTree(points: List<Point>, depth: Int): KDNode? {if (points.isEmpty()) {return null}val axis = depth % Kval sortedPoints = points.sortedWith(Comparator { a, b ->if (axis == 0) {a.x.compareTo(b.x)} else {a.y.compareTo(b.y)}})val medianIndex = sortedPoints.size / 2val node = KDNode(sortedPoints[medianIndex])node.left = buildTree(sortedPoints.subList(0, medianIndex), depth + 1)node.right = buildTree(sortedPoints.subList(medianIndex + 1, sortedPoints.size), depth + 1)return node}fun rangeSearch(lowerLeft: Point, upperRight: Point): List<Point> {val result: MutableList<Point> = ArrayList()rangeSearch(root, lowerLeft, upperRight, 0, result)return result}private fun rangeSearch(node: KDNode?,lowerLeft: Point,upperRight: Point,depth: Int,result: MutableList<Point>) {if (node == null) {return}val point = node.pointif (point.x >= lowerLeft.x && point.x <= upperRight.x && point.y >= lowerLeft.y && point.y <= upperRight.y) {result.add(point)}val axis = depth % Kif (axis == 0) {if (lowerLeft.x <= point.x) {rangeSearch(node.left, lowerLeft, upperRight, depth + 1, result)}if (upperRight.x >= point.x) {rangeSearch(node.right, lowerLeft, upperRight, depth + 1, result)}} else {if (lowerLeft.y <= point.y) {rangeSearch(node.left, lowerLeft, upperRight, depth + 1, result)}if (upperRight.y >= point.y) {rangeSearch(node.right, lowerLeft, upperRight, depth + 1, result)}}}companion object {private const val K = 2 // 2-dimensional space, e.g., x, y, z, t, etc}
}// Example usage
object KDTreeExample {@JvmStaticfun main(args: Array<String>) {val points: MutableList<Point> = ArrayList()points.add(Point(0.5, 0.5))points.add(Point(1.0, 1.0))points.add(Point(1.5, 1.5))points.add(Point(2.0, 2.0))points.add(Point(3.0, 3.0))val kdTree = KDTree(points)val lowerLeft = Point(0.0, 0.0)val upperRight = Point(1.5, 2.2)val result = kdTree.rangeSearch(lowerLeft, upperRight)for (point in result) {println(point)}}
}5. 注意事项
- 四叉树和KD树的构建和搜索时间复杂度取决于数据的分布和查询区域的大小。
- 四叉树和KD树都是用于空间数据索引和检索的有效数据结构。四叉树适用于二维空间,而KD树适用于多维空间。
- 在实际应用中,可以使用各种优化技术来提高性能,例如使用边界框、预分配内存等。
- 对于高维数据,KD树的性能可能会下降,可以使用其他数据结构,例如球树或随机投影树。
相关文章:

四叉树和KD树
1. 简介 四叉树和KD树都是用于空间数据索引和检索的树状数据结构。它们通过将空间递归地划分为更小的区域,并存储每个区域内的点,来实现快速搜索和范围查询。 2. 四叉树 2.1 定义 四叉树是一种树状数据结构,它将二维空间递归地划分为四个…...

C语言中结构体使用.与->访问成员变量的区别
文章目录 前言点运算符(.)箭头运算符(->)总结 前言 在C语言中,. 和 -> 都是用来访问结构体成员的运算符,但它们的使用场景和含义有所不同。 提示:以下是本篇文章正文内容,下面…...

计算机二级Access选择题考点
在Access中,若要使用一个字段保存多个图像、图表、文档等文件,应该设置的数据类型是附件。在“销售表"中有字段:单价、数量、折扣和金额。其中,金额单价x数量x折扣,在建表时应将字段"金额"的数据类型定义为计算。若…...

人工智能历史与现状
1 人工智能历史与现状 1.1 人工智能的概念和起源 1.1.1 人工智能的概念 人工智能 (Artificial Intelligence ,AI)是一门研究如何使计算机 能够模拟人类智能行为的科学和技术,目标在于开发能够感知、理解、 学习、推理、决策和解决问题的智能机器。人工智能的概念主要包含 以…...

【git使用一】windows下git下载、安装和卸载
目录 (1)下载安装包 (2)安装git (3)安装验证 (4)卸载git (1)下载安装包 官网下载地址:Git 国内镜像下载地址:CNPM Binaries Mir…...

JVM 类加载器的工作原理
JVM 类加载器的工作原理 类加载器(ClassLoader)是一个用于加载类文件的子系统,负责将字节码文件(.class 文件)加载到 JVM 中。Java 类加载器允许 Java 应用程序在运行时动态地加载、链接和初始化类。 2. 类加载器的工…...

ARM Cortex-M4 CPU指令大全:作用、原理与实例
引言 在计算机系统中,CPU(中央处理器)是执行各种指令的核心部件。ARM Cortex-M4是广泛应用于嵌入式系统中的一款处理器,其指令集架构(ISA)基于ARMv7-M。本文将介绍ARM Cortex-M4处理器中的常见指令&#x…...

Mysql学习(九)——存储引擎
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 七、存储引擎7.1 MySQL体系结构7.2 存储引擎简介7.3 存储引擎特点7.4 存储引擎选择7.5 总结 七、存储引擎 7.1 MySQL体系结构 连接层:最上层是一些客户…...
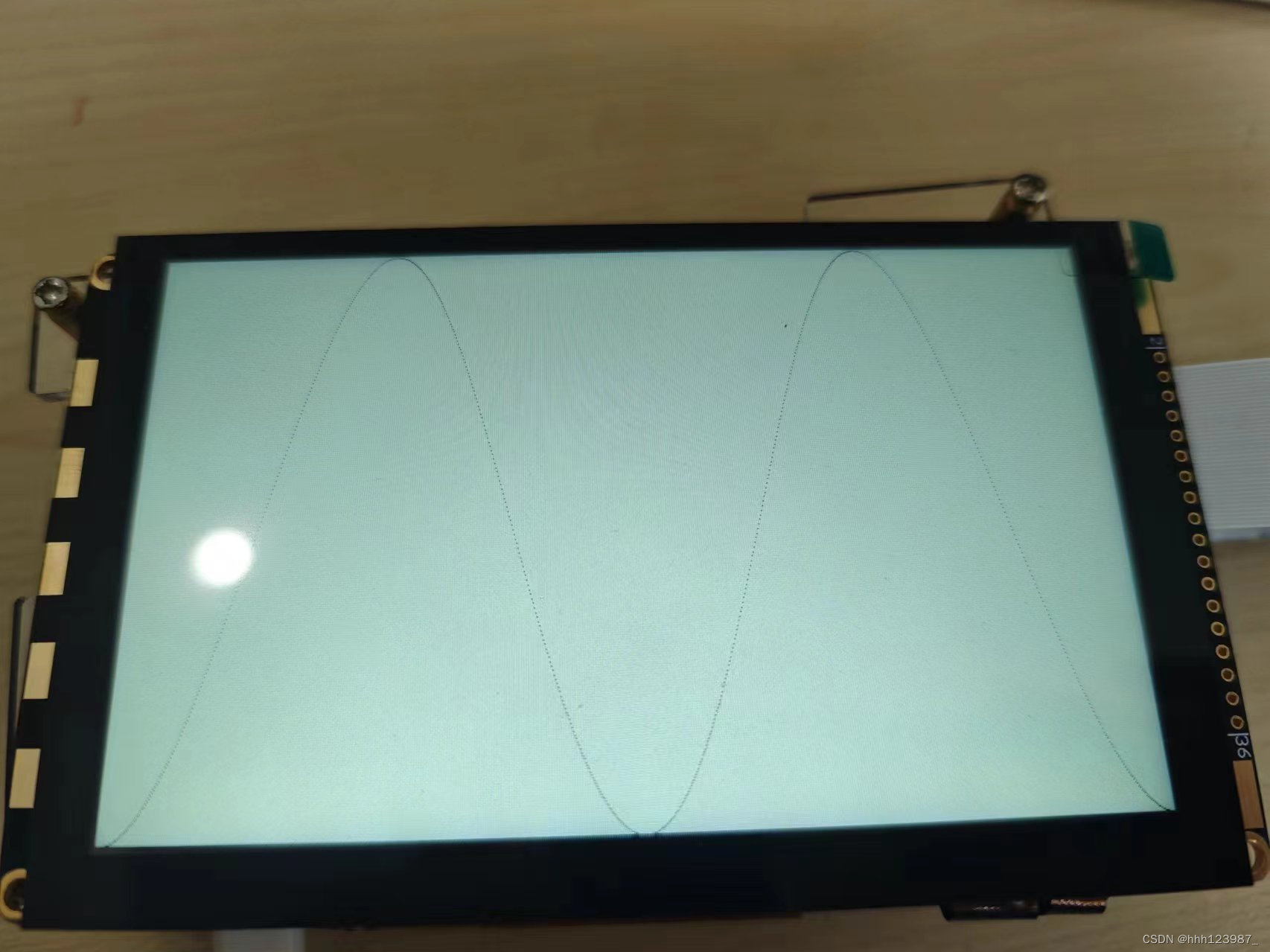
TFT屏幕波形显示
REVIEW 关于TFT显示屏,之前已经做过彩条显示: TFT显示屏驱动_tft驱动-CSDN博客 关于ROM IP核,以及coe文件生成: FPGA寄存器 Vivado IP核_fpga寄存器资源-CSDN博客 1. TFT屏幕ROM显示正弦波 ①生成coe文件 %% sin-cos wave dat…...
服务器无法远程桌面连接不上的问题排查与解决方案
一、问题概述 当尝试使用远程桌面协议(RDP)连接至服务器时,如果连接失败,这通常意味着存在一些配置问题、网络问题或服务器本身的问题。此类问题对于管理员而言,需要系统地进行排查和解决。 二、排查步骤 1. 检查网…...

JAVA面试题整理——内存溢出与内存泄露的区别与联系
内存溢出与内存泄露的区别与联系 在前面jvm学习整理的时候其实用过一个简单的例子了解过内存溢出,在jvm内存模型章节下,大家有兴趣的可以去看看:JVM初学 GC_knowwait的博客-CSDN博客 内存溢出 内存溢出(out of memory)…...

L50--- 104. 二叉树的最大深度(深搜)---Java版
1.题目描述 二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。 2.思路 这个二叉树的结构如下: 根节点 1 左子节点 2 右子节点 3 左子节点 4 计算过程 从根节点 1 开始计算: 计算左子树的最大深度: 根节点 2…...

Linux 中 “ 磁盘、进程和内存 ” 的管理
在linux虚拟机中也有磁盘、进程、内存的存在。第一步了解一下磁盘 一、磁盘管理 (1.1)磁盘了解 track( 磁道 ) :就是磁盘上的同心圆,从外向里,依次排序1号,2号磁盘........等等。…...

test_pipeline
test_pipeline 是一个测试管道(test pipeline)的定义。 在计算机视觉任务中,通常需要对输入图像进行一系列的预处理操作,以便将其适配到模型的输入要求或提高模型的性能。测试管道就是用于定义这些预处理操作的一系列步骤。 在给…...

使用甲骨文云arm服务器安装宝塔时nginx无法卸载
使用甲骨文云arm服务器安装宝塔 其他环境都能安装上 唯独nginx安装完不运行 卸载了几次以后还无法卸载了. 修复 重启都不行. 差点就重建主机了. 最后靠下面的命令 就卸载掉了 然后重装就把nginx安装好了 mv /www/server/nginx/sbin/nginx /tmp/nginx_back mv /etc/in…...

C++青少年简明教程:C++的指针入门
C青少年简明教程:C的指针入门 说到指针,就不可能脱离开内存。了解C的指针对于初学者来说可能有些复杂,我们可以试着以一种简单、形象且易于理解的方式来解释: 首先,我们可以将计算机内存想象成一个巨大的有许多格子的…...
)
Apache Doris 基础 -- 数据表设计(分层存储)
1、应用场景 未来一个重要的用例是类似于ES日志存储,其中日志场景中的数据是根据日期分割的。许多数据都是查询不频繁的冷数据,因此需要降低此类数据的存储成本。考虑到节约成本: 来自不同厂商的常规云磁盘的定价比对象存储更昂贵。Doris 集群实际在线…...

使用Spring Boot设计一套BI系统
商业智能(Business Intelligence,简称BI)系统是一种将数据转化为可操作信息,帮助企业进行决策支持的技术与工具的集合。随着大数据时代的到来,BI系统在企业中的应用变得越来越广泛。本文旨在探讨如何使用Spring Boot框…...

2024.6.12总结
今天是排毕业照的日子,拍照的时候并没有太过兴奋。后来受到主管说明天就能签offer了,这才喜极而泣。 自从得知自己面试通过后,我是非常高兴,开始幻想着今后的生活。可是,后面在等offer的过程中,我是无比的…...

1027 - 求任意三位数各个数位上数字的和
问题描述 对于一个任意的三位自然数 x ,编程计算其各个数位上的数字之和 S 。 输入 输入一行,只有一个整数 x(100≤x≤999) 。 输出 输出只有一行,包括 1 个整数。 样例 输入 123 输出 6 以下是C实现的代码: 代码1 #…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

【Linux】Linux 系统默认的目录及作用说明
博主介绍:✌全网粉丝23W,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...
详细解析)
Caliper 负载(Workload)详细解析
Caliper 负载(Workload)详细解析 负载(Workload)是 Caliper 性能测试的核心部分,它定义了测试期间要执行的具体合约调用行为和交易模式。下面我将全面深入地讲解负载的各个方面。 一、负载模块基本结构 一个典型的负载模块(如 workload.js)包含以下基本结构: use strict;/…...

通过MicroSip配置自己的freeswitch服务器进行调试记录
之前用docker安装的freeswitch的,启动是正常的, 但用下面的Microsip连接不上 主要原因有可能一下几个 1、通过下面命令可以看 [rootlocalhost default]# docker exec -it freeswitch fs_cli -x "sofia status profile internal"Name …...

pycharm 设置环境出错
pycharm 设置环境出错 pycharm 新建项目,设置虚拟环境,出错 pycharm 出错 Cannot open Local Failed to start [powershell.exe, -NoExit, -ExecutionPolicy, Bypass, -File, C:\Program Files\JetBrains\PyCharm 2024.1.3\plugins\terminal\shell-int…...
实现跳一跳小游戏)
鸿蒙(HarmonyOS5)实现跳一跳小游戏
下面我将介绍如何使用鸿蒙的ArkUI框架,实现一个简单的跳一跳小游戏。 1. 项目结构 src/main/ets/ ├── MainAbility │ ├── pages │ │ ├── Index.ets // 主页面 │ │ └── GamePage.ets // 游戏页面 │ └── model │ …...

恶补电源:1.电桥
一、元器件的选择 搜索并选择电桥,再multisim中选择FWB,就有各种型号的电桥: 电桥是用来干嘛的呢? 它是一个由四个二极管搭成的“桥梁”形状的电路,用来把交流电(AC)变成直流电(DC)。…...
