java算法:选择排序
文章标题
- 概述与基本实现
- 优缺点
- 尝试优化
概述与基本实现
选择排序(Selection Sort)是一种简单直观的排序算法。它的基本思想是每次从待排序的元素中选择最小(或最大)的元素,放置在已排序的部分的末尾,直到所有元素都排序完成。
实现步骤:
- 遍历数组,将当前位置作为最小值的索引(假设为minIndex)。
- 在未排序部分中遍历数组,从当前位置开始,找到最小值的索引。
- 将最小值与当前位置的元素交换位置。这样,最小值将会被放置在已排序部分的末尾。
- 重复步骤2和3,直到整个数组排序完成。
public class SelectionSort {public static void selectionSort(int[] arr) {int n = arr.length;// 遍历数组for (int i = 0; i < n - 1; i++) {int minIndex = i; // 当前位置作为最小值的索引// 在未排序部分找到最小值的索引for (int j = i + 1; j < n; j++) {if (arr[j] < arr[minIndex]) {minIndex = j;}}// 将最小值与当前位置的元素交换位置int temp = arr[minIndex];arr[minIndex] = arr[i];arr[i] = temp;}}public static void main(String[] args) {int[] arr = {64, 25, 12, 22, 11};System.out.println("原始数组: " + Arrays.toString(arr));selectionSort(arr);System.out.println("排序后数组: " + Arrays.toString(arr));}
}
通过选择排序算法,数组按升序进行了排序。在每次循环中,选择排序会找到未排序部分的最小值,并将其放置在已排序部分的末尾,直到整个数组排序完成。选择排序的时间复杂度为O(n^2),其中n是数组的大小。
优缺点
优点:
- 简单直观:选择排序算法的实现相对简单,容易理解和实现。
- 不占用额外空间:选择排序算法是在原地进行排序的,不需要额外的辅助空间。
- 稳定性:选择排序是一种稳定的排序算法,不会改变相等元素的相对顺序。
缺点:
- 时间复杂度:选择排序的时间复杂度为O(n^2),其中n是数组的大小。在最坏情况下,无论输入数据的顺序如何,都需要进行n*(n-1)/2次比较和n次交换操作。
- 不适用于大规模数据:由于选择排序的时间复杂度较高,它在处理大规模数据时效率较低,不如其他高效的排序算法(如快速排序、归并排序等)。
- 不稳定的选择性:尽管选择排序是一种稳定的排序算法,但在选择最小值的过程中,交换操作可能会打破相等元素的相对顺序,导致不稳定性。
选择排序算法在简单性和稳定性方面具有一些优点,但在时间复杂度和适用性上存在一些缺点。对于小规模的数据或者对稳定性要求较高的场景,选择排序可能是一个合适的选择。然而,对于大规模数据或对性能有较高要求的情况,其他更高效的排序算法通常更合适。
尝试优化
选择排序算法在简单性和稳定性方面具有一些优点,但在时间复杂度和适用性上存在一些缺点。对于小规模的数据或者对稳定性要求较高的场景,选择排序可能是一个合适的选择。然而,对于大规模数据或对性能有较高要求的情况,其他更高效的排序算法通常更合适。
优化选择排序的方法:
- 最小值和最大值同时查找:传统的选择排序算法会先找到最小值的索引,然后进行交换。但实际上,在同一次遍历中,可以同时找到最小值和最大值的索引,然后进行两个位置的交换。这样可以减少一半的比较次数。
- 减少交换次数:传统的选择排序算法在找到最小值或最大值后会立即进行交换。但可以优化为先记录最小值(或最大值)的索引,然后在一次遍历结束后再进行交换。这样可以减少交换的次数。
示例代码:
public class SelectionSort {public static void selectionSort(int[] arr) {int n = arr.length;for (int i = 0; i < n - 1; i++) {int minIndex = i;int maxIndex = i;for (int j = i + 1; j < n; j++) {if (arr[j] < arr[minIndex]) {minIndex = j;} else if (arr[j] > arr[maxIndex]) {maxIndex = j;}}// 将最小值交换到已排序部分的开头if (minIndex != i) {int temp = arr[minIndex];arr[minIndex] = arr[i];arr[i] = temp;}// 如果最大值的索引发生了交换,重新调整最大值的索引if (maxIndex == i) {maxIndex = minIndex;}// 将最大值交换到已排序部分的末尾if (maxIndex != n - 1) {int temp = arr[maxIndex];arr[maxIndex] = arr[n - 1];arr[n - 1] = temp;}n--; // 已排序部分增加一个元素,未排序部分减少一个元素}}public static void main(String[] args) {int[] arr = {64, 25, 12, 22, 11};System.out.println("原始数组: " + Arrays.toString(arr));selectionSort(arr);System.out.println("排序后数组: " + Arrays.toString(arr));}
}
通过同时查找最小值和最大值的索引,并在一次遍历结束后进行交换,可以减少比较和交换的次数。这样的优化可以稍微提高选择排序的性能。
需要注意的是,尽管选择排序经过优化,但其时间复杂度仍然是O(n^2),并不适用于大规模数据。对于更高效的排序算法,如快速排序、归并排序等,可以考虑使用它们来取代选择排序。
相关文章:

java算法:选择排序
文章标题 概述与基本实现优缺点尝试优化 概述与基本实现 选择排序(Selection Sort)是一种简单直观的排序算法。它的基本思想是每次从待排序的元素中选择最小(或最大)的元素,放置在已排序的部分的末尾,直到…...
helm升级部署时出现升级挂起状态处理
问题 在使用helm 升级命令时,升级命令如下: helm upgrade -i -f ./values-prod.yaml myapp ./ -n myns --create-namespace中途因为网络原因,再次运行上面升级命令时出现,如下错误: Error: UPGRADE FAILED: another …...

16、架构-可观测性-事件日志详细解析
事件日志 事件日志是记录系统运行期间发生的离散事件的关键工具。它们在系统的可观测性中起着至关重要的作用,帮助开发者和运维人员追踪、分析和解决系统问题。以下是对事件日志处理各个方面的详细解析,并结合具体的数据案例和技术支撑。 输出 日志输出…...
)
Java数据结构与算法(买卖股票的最佳时机二贪心算法)
前言 买卖股票最佳时机二,此时不限次数的买卖的要求获得的利益最大化。暴力算法依旧可行,可以参考之前的练习。 . - 力扣(LeetCode) 贪心算法原理参考:Java数据结构与算法(盛水的容器贪心算法)-CSDN博客 实现原理 1.定义最大…...

t265 坑
Streaming T265 video over USB 2.1 is unreliable, please use USB 3 or only stream poses 试着用windows 打开也是默认是USB2打开, 英伟达orin nx jetpack 也一样 不知道为啥。并且一旦打开飞控 microxrceagent , t265 的位置就飞。 配置ros2 的lau…...
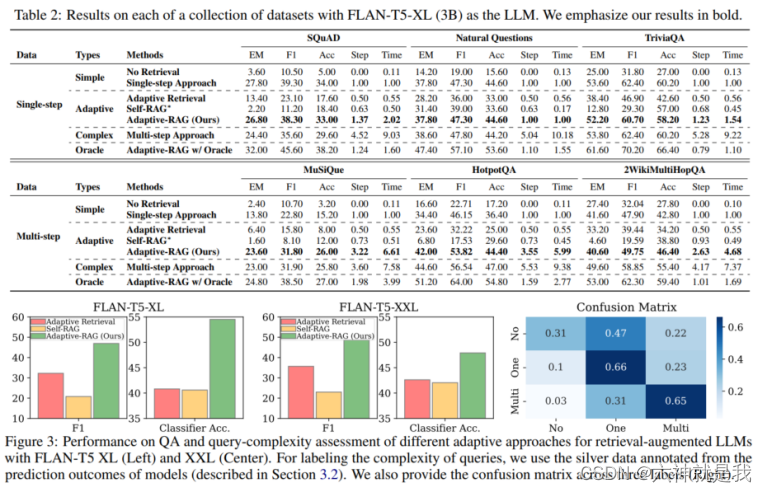
【LLM之RAG】Adaptive-RAG论文阅读笔记
研究背景 文章介绍了大型语言模型(LLMs)在处理各种复杂查询时的挑战,特别是在不同复杂性的查询处理上可能导致不必要的计算开销或处理不足的问题。为了解决这一问题,文章提出了一种自适应的查询处理框架,动态选择最合…...

介绍react
什么是React React是一个用于构建用户界面的JavaScript库。 传统构建页面的方式 <script>document.getElementById(app).addEventListener(click, () > {console.log()});const div docuemnt.createElement(div)// ... </script> 早期,用JavaSc…...

网络爬虫概述
自学python如何成为大佬(目录):https://blog.csdn.net/weixin_67859959/article/details/139049996?spm1001.2014.3001.5501 网络爬虫(又被称为网络蜘蛛、网络机器人,在某社区中经常被称为网页追逐者),可以按照指定的规则&#…...
取证工作: SysTools SQL Log Analyzer, 完整的 SQL Server 日志取证分析
天津鸿萌科贸发展有限公司是 Systools 系列软件的授权代理商。 SysTools SQL Log Analyzer 是 Systools 取证工具系列之一,用于调查 SQL Server 事务日志,以对数据库篡改进行取证分析。 什么是 SQL Server 事务日志? 在深入研究 SQL 事务日…...
蓝牙耳机怎么连接电脑?轻松实现无线连接
蓝牙耳机已经成为许多人生活中不可或缺的一部分,不仅可以方便地连接手机,还能轻松连接电脑,让我们在工作和娱乐时享受无线的自由。然而,对于一些用户来说,将蓝牙耳机与电脑连接可能会遇到一些问题。本文将介绍蓝牙耳机…...
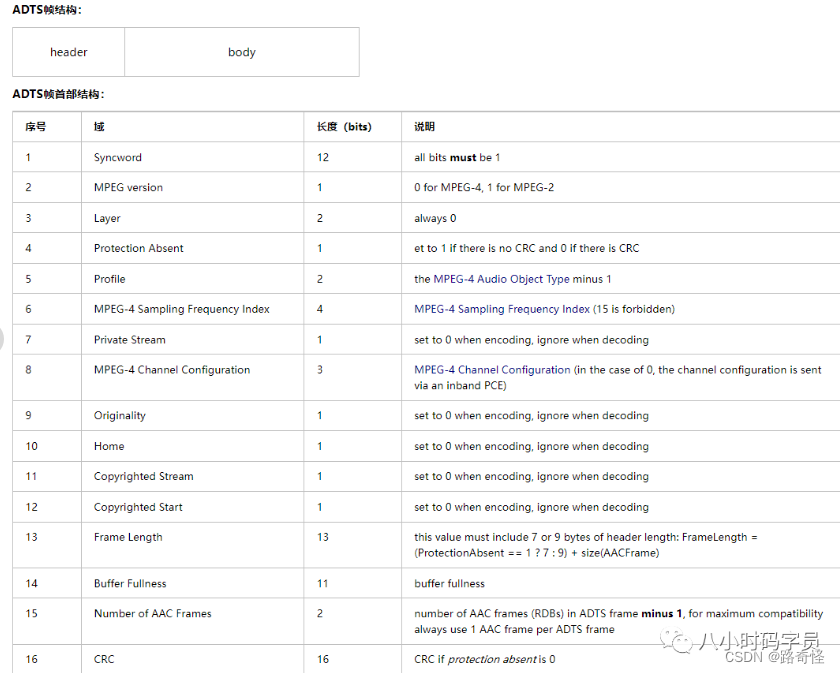
4.音视频 AAC SSAASS
目录 AAC 1.什么是ADIF和ADTS? 2.ADTS的数据结构是怎样的? SSA/ASS 1.SSA/ASS的基本结构 AAC AAC(Advanced Audio Coding,高级音频编码)是一种声音数据的文件压缩格式。AAC分为ADIF和ADTS两种文件格式。 1.什么是ADIF和ADTSÿ…...

每日5题Day24 - LeetCode 116 - 120
每一步向前都是向自己的梦想更近一步,坚持不懈,勇往直前! 第一题:116. 填充每个节点的下一个右侧节点指针 - 力扣(LeetCode) /* // Definition for a Node. class Node {public int val;public Node left;…...

在笔记本电脑上使用 LLMs 的 5 种方法
在网上使用 ChatGPT 很简单,只需有网络连接和好的浏览器即可。但这样做可能会泄露您的隐私和数据。OpenAI 存储了您的提示和其他元数据以重新训练模型。对于一些人来说可能不成问题,但注重隐私的人可能更愿意在本地使用这些模型,不受外部跟踪…...
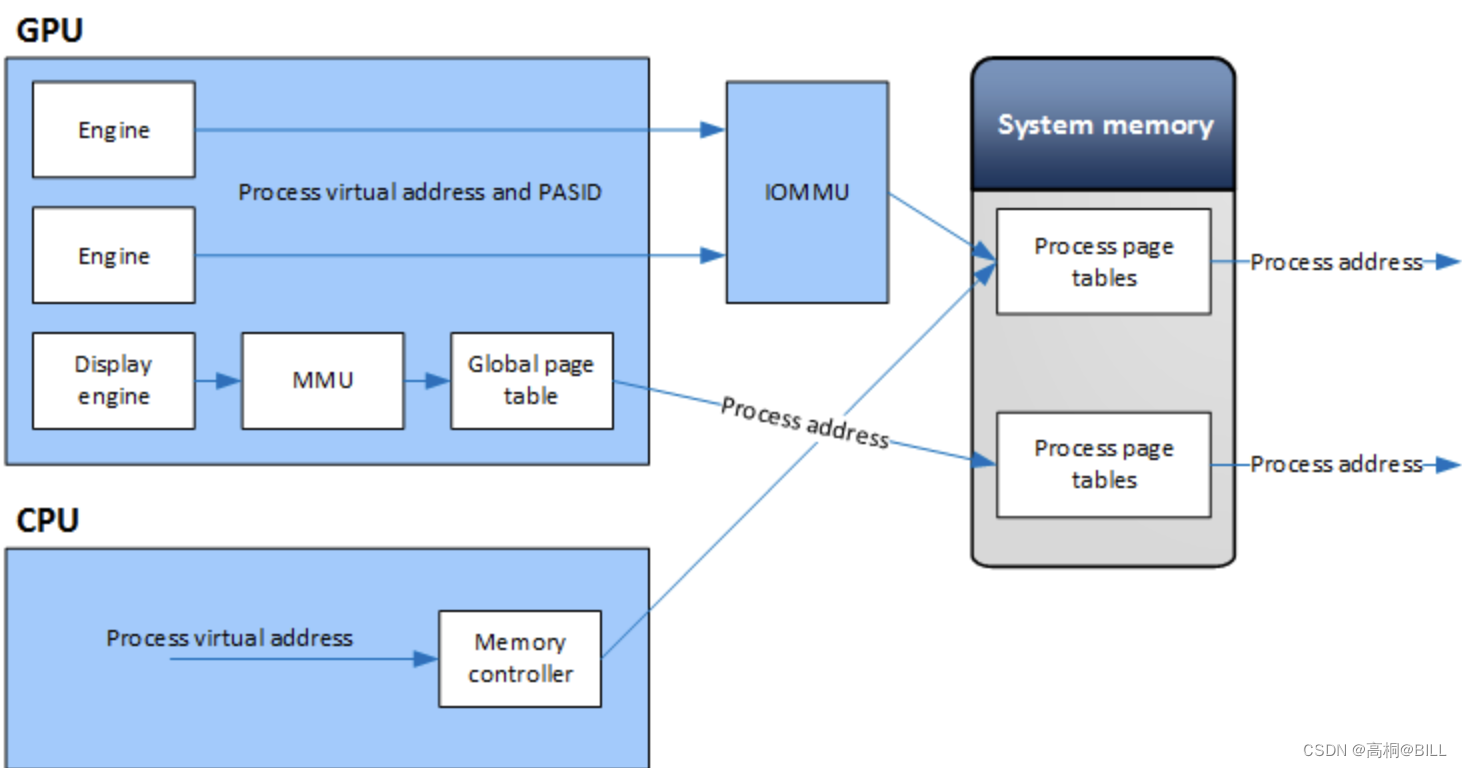
Linux内存从0到1学习笔记(8.15 MMU/IOMMU/SMMU概览)
一, 什么是MMU? MMU(Memory Management Unit 内存管理单元),即内存管理单元,是计算机硬件中的一个重要组件,主要负责处理中央处理器(CPU)的内存访问请求。 其工作原理如下: 当程序发出内存访问请求,包括读取或写入操作以及逻辑地址(虚拟地址)。然后,MMU根据页表…...

Intellij IDEA中怎么配置Maven?
在IntelliJ IDEA中配置Maven非常简单,以下是详细步骤: 步骤1:安装Maven 首先确保你的计算机上已经安装了Maven。如果没有安装,你可以从Apache Maven官网下载并安装:https://maven.apache.org/download.cgi 步骤2&am…...
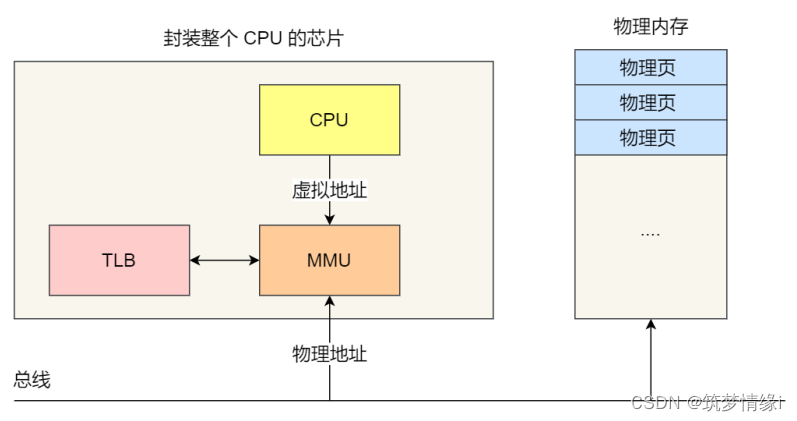
操作系统-内存管理
虚拟内存 操作系统会提供⼀种机制,将不同进程的虚拟地址和不同内存的物理地址映射起来。 两个概念: 程序所使⽤的内存地址叫做虚拟内存地址(Virtual Memory Address)实际存在硬件⾥⾯的空间地址叫物理内存地址(Physi…...

C++中的解释器模式
目录 解释器模式(Interpreter Pattern) 实际应用 算术表达式解释器 布尔表达式解释器 总结 解释器模式(Interpreter Pattern) 解释器模式是一种行为设计模式,它定义了一种语言的文法表示,并使用解释器…...

用 C 语言实现求补码的运算
缘起 前两天程序中需要求一堆参数的补码,一时犯懒,想从CSDN上搜一个勉强能用的代码借鉴一下,结果几乎没有搜到一个靠谱的!这种求补码的操作,用脚趾头想想也应该知道要用C或者C的位运算来实现呀。结果搜到的一些实现方…...

python下载文件
import urllib.request url "http://****/storage/x4MigEhU6BGAuTqjrRfIBky0S2aMmkyGl4UzTqUb.png"#下载地址 path "ddad.png"#保存路径,保存项目路径 urllib.request.urlretrieve(url, path)...
)
JMU 数科 数据库与数据仓库期末总结(1)
本章根据老师给出的知识点作进一步相对生动一点的解释。 不保证完全正确。 先给出总的知识点,再给出生动解释。 知识点 数据模型通常由三部分组成:数据结构、数据操作和完整性约束。关系模式中主码的取值必须唯一且非空,这是实体完整性的…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...
