Pytorch模型参数的保存和加载
目录
一、前言
二、参数保存
三、参数的加载
四、保存和加载整个模型
五、总结
一、前言
在模型训练完成后,我们需要保存模型参数值用于后续的测试过程。由于保存整个模型将耗费大量的存储,故推荐的做法是只保存参数,使用时只需在建好模型的基础上加载。
通常来说,保存的对象包括网络参数值、优化器参数值、epoch值等。本文将简单介绍保存和加载模型参数的方法,同时也给出保存整个模型的方法供大家参考。
二、参数保存
在这里我们使用 torch.save() 函数保存模型参数:
import torch
path = './model.pth'
torch.save(model.state_dict(), path)model——指定义的模型实例变量,如model=net( )
state_dict()——state_dict( )是一个可以轻松地保存、更新、修改和恢复的python字典对象, 对于model来说,表示模型的每一层的权重及偏置等参数信息;对于 optimizer 来说,其包含了优化器的状态以及被使用的超参数(如lr, momentum,weight_decay等)
path——path是保存参数的路径,一般设置为 path='./model.pth' , path='./model.pkl'等形式。
此外,如果想保存某一次训练采用的optimizer、epochs等信息,可将这些信息组合起来构成一个字典保存起来:
import torch
path = './model.pth'
state = {'model': model.state_dict(), 'optimizer': optimizer.state_dict(), 'epoch': epoch}
torch.save(state, path)三、参数的加载
使用 load_state_dict()函数加载参数到模型中, 当仅保存了模型参数,而没有optimizer、epochs等信息时:
model.load_state_dict(torch.load(path))model——事先定义好的跟原模型一致的模型
path——之前保存的模型参数文件
如若保存了optimizer、epochs等信息,我们这样载入信息:
# 使用torch.load()函数将文件中字典信息载入 state_dict 变量中
state_dict = torch.load(path)
# 分布加载参数到模型和优化器
model.load_state_dict(state_dict['model'])
optimizer.load_state_dict(state_dict['optimizer'])
epoch = state_dict(['epoch'])我们还可以在每n个epoch后保存一次参数,以观察不同迭代次数模型的表现。此时我们可设置不同的path,如 path='./model' + str(epoch) +'.pth',这样,不同epoch的参数就能保存在不同的文件中。
四、保存和加载整个模型
使用上文提到的方法即可:
torch.save(model, path)
model = torch.load(path)五、总结
pytorch中state_dict()和load_state_dict()函数配合使用可以实现状态的获取与重载,load()和save()函数配合使用可以实现参数的存储与读取。掌握对应的函数使用方法就可以游刃有余地进行运用。
相关文章:

Pytorch模型参数的保存和加载
目录 一、前言 二、参数保存 三、参数的加载 四、保存和加载整个模型 五、总结 一、前言 在模型训练完成后,我们需要保存模型参数值用于后续的测试过程。由于保存整个模型将耗费大量的存储,故推荐的做法是只保存参数,使用时只需在建好模…...
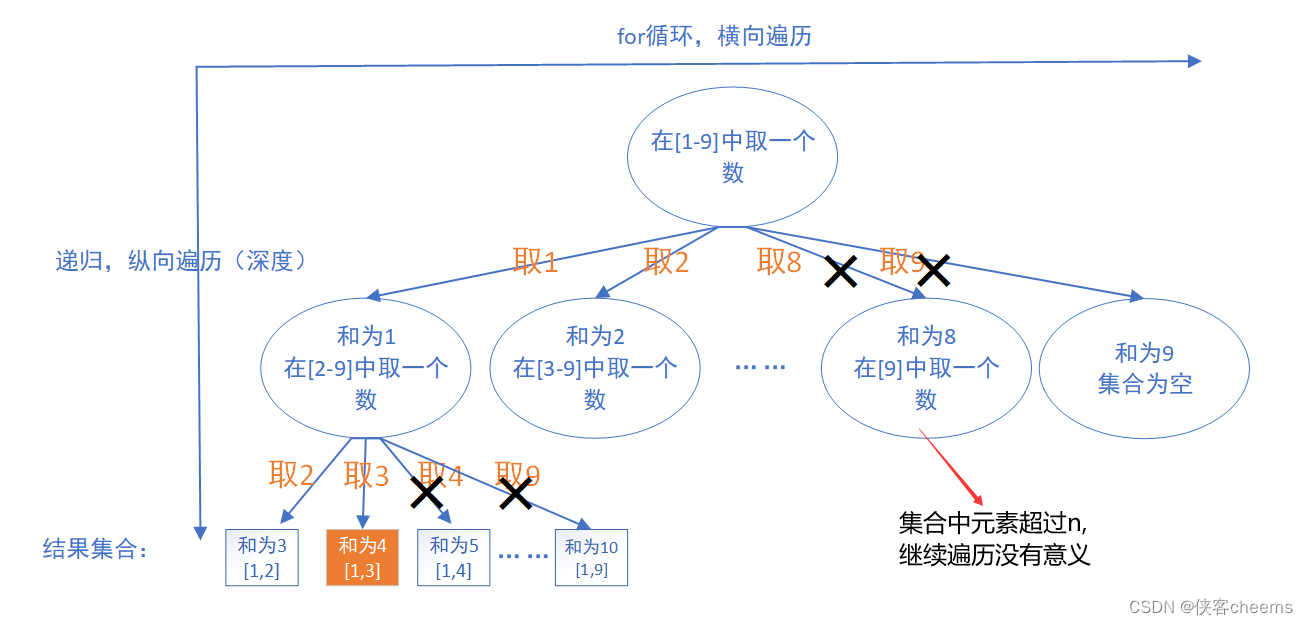
面试热点题:回溯算法之组合 组合与组合总和 III
什么是回溯算法? 回溯算法也可以叫回溯搜索算法,回溯是递归的"副产品",回溯的本质是穷举,然后选出我们需要的数据,回溯本身不是特别高效的算法,但我们可以通过"剪枝"来优化它。 理解回溯算法 回溯…...
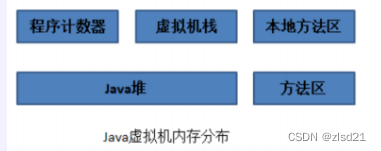
java面试-jvm
JVM JVM 是 java 虚拟机,简单来说就是能执行标准 java 字节码的虚拟计算机 JVM 是如何工作的 首先程序在执行之前先要把 Java 代码(.java)转换成字节码(.class),JVM 通过类加载器(ClassLoade…...
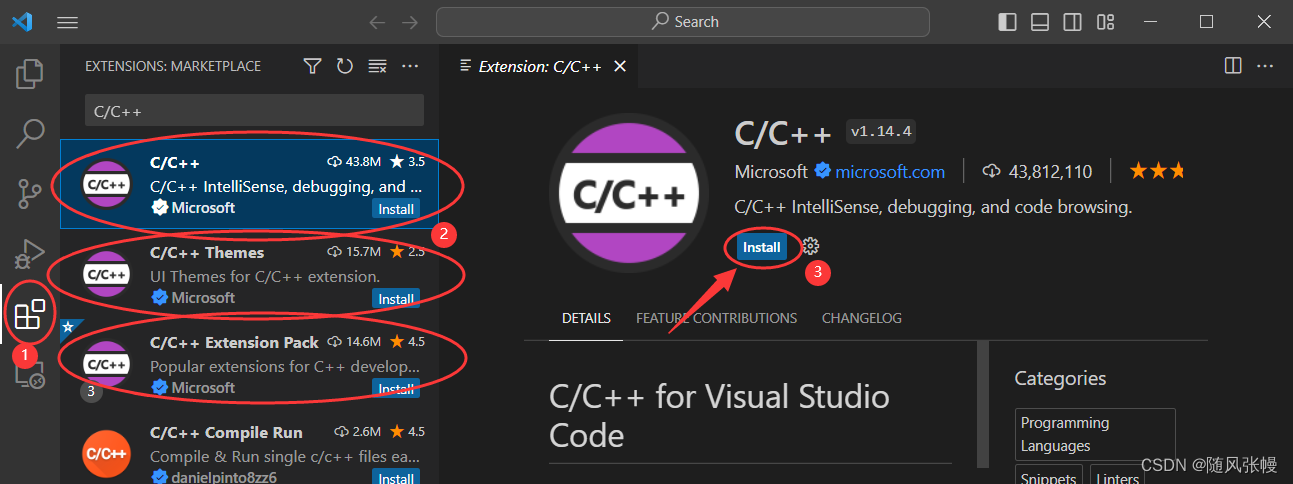
vscode下载与使用
1.vscode下载 官网下载地址:Download Visual Studio Code - Mac, Linux, Windows下载太慢,推荐文章:解决VsCode下载慢问题_vscode下载太慢_迷小圈的博客-CSDN博客下载太慢,推荐下载链接:https://vscode.cdn.azure.cn/s…...

人员摔倒识别预警算法 opencv
人员摔倒识别预警算法通过opencv网络模型技术,人员摔倒识别预警算法能够智能检测现场画面中人员有没有摔倒,无需人为干预可以立刻抓拍告警。OpenCV的全称是Open Source Computer Vision Library,是一个跨平台的计算机视觉处理开源软件库&…...
| 机考必刷)
华为OD机试题 - 火星文计算(JavaScript)| 机考必刷
更多题库,搜索引擎搜 梦想橡皮擦华为OD 👑👑👑 更多华为OD题库,搜 梦想橡皮擦 华为OD 👑👑👑 更多华为机考题库,搜 梦想橡皮擦华为OD 👑👑👑 华为OD机试题 最近更新的博客使用说明本篇题解:火星文计算题目输入输出示例一输入输出说明Code解题思路版权说明…...

AI人工智能 - 初探
1.应用场景 主要用于了解和系统学习AI,从而可以在工作生活中利用AI做一些事。 2.学习/操作 1.文档阅读 下面的内容来自于与chatGPT的对话 2.整理输出 介绍AI 人工智能(Artificial Intelligence,简称AI)是计算机科学中的一个分支&…...

Spring-AOP工作流程
Spring-AOP工作流程 3,AOP工作流程 3.1 AOP工作流程 由于AOP是基于Spring容器管理的bean做的增强,所以整个工作过程需要从Spring加载bean说起: 流程1:Spring容器启动 容器启动就需要去加载bean,哪些类需要被加载呢?需要被增强的类,如:B…...

C51---串口发送指令,控制LED灯亮灭
1.Code: #include "reg52.h" #include "intrins.h" sfr AUXR 0x8E; sbit D5 P3^7; void UartInit(void) //9600bps11.0592MHz { //PCON & 0x7F; //波特率不倍速 AUXR 0x01; SCON 0x50; //8位数据,可变波…...

【Wiki】XWiki数据备份
XWiki为主题使用java开发的开源wiki,官网地址如下: https://www.xwiki.org/xwiki/bin/view/Main/ 目录1、 XWiki升级数据备份1.1、 获取XWiki配置的数据库与持久化目录信息1.2 备份数据库信息1.3 备份持久化目录2、XWiki数据迁移如果一个知识库不能确保数…...

ctk框架开发Qt插件应用示例工程
目录 前言 约定 插件工程pluginApp: 主启动工程StartApp: 效果演示 结语...
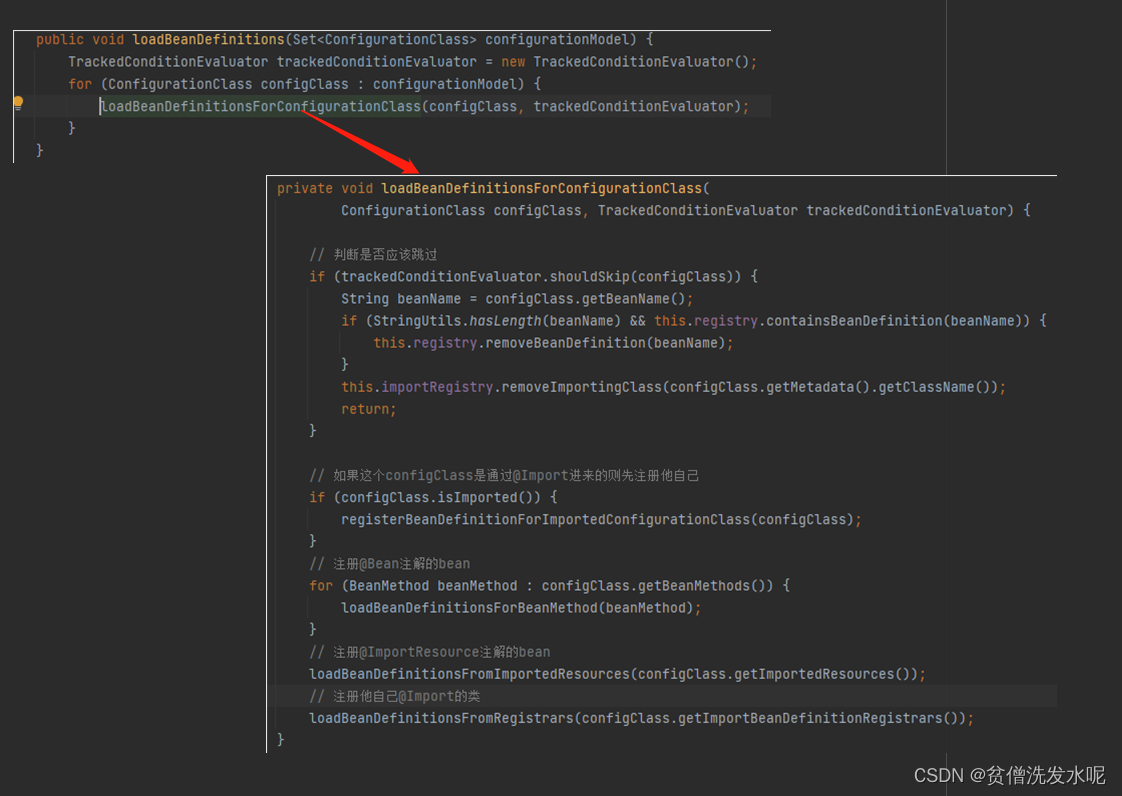
spring5源码篇(4)——beanFactoryPostProcessor执行/注解bean的装配
spring-framework 版本:v5.3.19 前面研究了beanDefinition的注册,但也仅仅是注册这一动作。那么在spring容器启动的过程中,是何时/如何装配的?以及装配的bean是如何注入的? (考虑到xml方式基本不用了以及篇…...

masstransit的message几个高级用法
1)问题,Class MessageA 基类,Class MessageB继承自MessageA; 用bus.Publish方法本想把有些消息只发给B队列,结果由于其继承关系A队列也获得了消息; 解决方法用send, Uri uri new Uri(RabbitM…...

漏洞分析丨cve-2012-0003
作者:黑蛋一、漏洞简介这次漏洞属于堆溢出漏洞,他是MIDI文件中存在的堆溢出漏洞。在IE6,IE7,IE8中都存在这个漏洞。而这个漏洞是Winmm.dll中产生的。二、漏洞环境虚拟机调试工具目标软件辅助工具XP-SP3、KaliOD、IDAIE6Windbg组件gflags.exe三…...

rm命令——删除文件或目录
rm命令是英文单词remove的缩写,主要功能是删除文件或目录。 因为删除文件是一个破坏性动作,因此,在使用时需要格外小心,在执行之前一定要再三确认删除的是哪个目录中的什么文件。 rm命令的语法格式如下: rm [选项] …...

【零基础入门学习Python---Python的基本语法使用】
一.Python基本语法使用 Python是一种易学且功能强大的编程语言,具有简洁的语法和广泛的应用领域。在本文中,我们将介绍Python的基本语法使用,以帮助初学者快速入门Python编程。 1.1 注释 Python 支持两种类型的注释:单行注释和多行注释。 单行注释:以 # 符号开头,从 # …...

数据仓库相关概念的解释
数据仓库相关概念的解释 文章目录数据仓库相关概念的解释1 ETL是什么?ETL体系结构2 数据流向何为数仓DW3 ODS 是什么?4 数据仓库层DWDWD 明细层DWD 轻度汇总层(MID或DWB,data warehouse basis)DWS 主题层(D…...
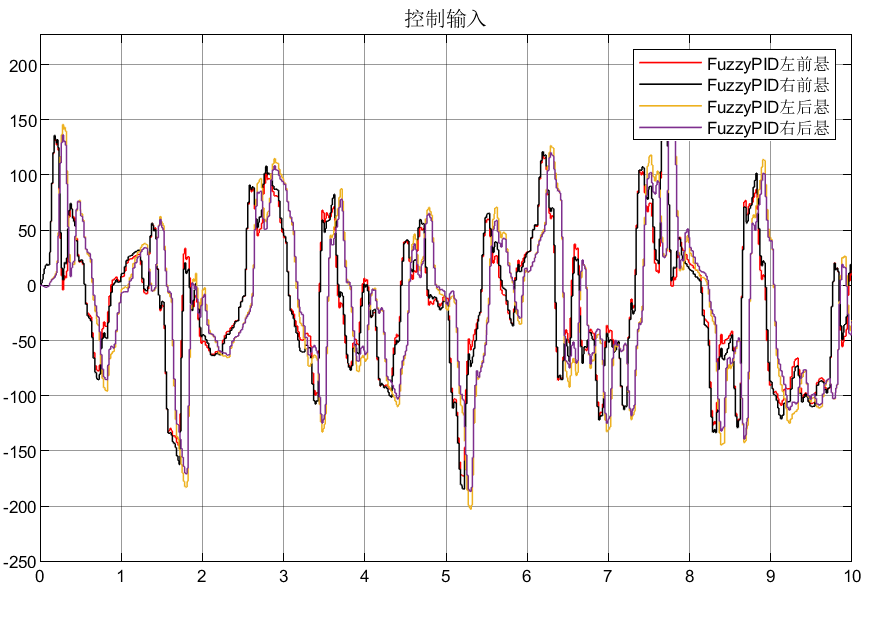
1/4车、1/2车、整车悬架模糊PID控制仿真合集
目录 前言 1. 1/4悬架系统 1.1数学模型 1.2仿真分析 2. 1/2悬架系统 2.1数学模型 2.2仿真模型 2.3仿真分析 3. 整车悬架系统 3.1数学模型 3.2仿真分析 4.总结 前言 前面几篇文章介绍了LQR、SkyHook、H2/H∞、PID控制,接下来会继续介绍滑模、反步法、M…...

Linux性能补丁升级,避免不必要的跨核Wake-Up
导读一个由英特尔发起的、旨在改进Linux内核公平调度程序代码的补丁系列,也看到了来自AMD工程师和其他利益相关者的测试/反馈,并继续进行改进。这个补丁系列的重点是避免在不必要的情况下发生过多的跨核唤醒(Cross-CPU Wake-up)。这样一来,这…...

Spring Cloud Alibaba全家桶(六)——微服务组件Sentinel介绍与使用
前言 本文小新为大家带来 微服务组件Sentinel介绍与使用 相关知识,具体内容包括分布式系统存在的问题,分布式系统问题的解决方案,Sentinel介绍,Sentinel快速开始(包括:API实现Sentinel资源保护,…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...

xmind转换为markdown
文章目录 解锁思维导图新姿势:将XMind转为结构化Markdown 一、认识Xmind结构二、核心转换流程详解1.解压XMind文件(ZIP处理)2.解析JSON数据结构3:递归转换树形结构4:Markdown层级生成逻辑 三、完整代码 解锁思维导图新…...

从实验室到产业:IndexTTS 在六大核心场景的落地实践
一、内容创作:重构数字内容生产范式 在短视频创作领域,IndexTTS 的语音克隆技术彻底改变了配音流程。B 站 UP 主通过 5 秒参考音频即可克隆出郭老师音色,生成的 “各位吴彦祖们大家好” 语音相似度达 97%,单条视频播放量突破百万…...

基于stm32F10x 系列微控制器的智能电子琴(附完整项目源码、详细接线及讲解视频)
注:文章末尾网盘链接中自取成品使用演示视频、项目源码、项目文档 所用硬件:STM32F103C8T6、无源蜂鸣器、44矩阵键盘、flash存储模块、OLED显示屏、RGB三色灯、面包板、杜邦线、usb转ttl串口 stm32f103c8t6 面包板 …...

Win系统权限提升篇UAC绕过DLL劫持未引号路径可控服务全检项目
应用场景: 1、常规某个机器被钓鱼后门攻击后,我们需要做更高权限操作或权限维持等。 2、内网域中某个机器被钓鱼后门攻击后,我们需要对后续内网域做安全测试。 #Win10&11-BypassUAC自动提权-MSF&UACME 为了远程执行目标的exe或者b…...
