当前位置： 首页 > news >正文

主题切换之根元素CSS自定义类

news 2026/2/9 4:47:55

要实现CSS样式的主题切换，可以通过在HTML中添加一个按钮来触发JavaScript事件，进而通过JavaScript动态修改HTML元素的class或直接切换CSS文件，以达到改变页面整体风格的目的。以下是实现这一功能的步骤、原理及代码示例。

原理：

  1. HTML结构：提供一个用户界面元素（如按钮）来触发切换操作。
  2. CSS样式：定义两套样式，一套为默认主题，另一套为备用主题（比如夜间模式）。备用主题的样式通常通过类名（如.night-mode)来控制。
  3. JavaScript：编写逻辑来响应用户的切换请求，通过修改HTML元素的class或更改<link>标签的href属性来应用新的主题样式。

示例代码：

HTML (index.html)
html<!DOCTYPE html>
<html lang="en">
<head><meta charset="UTF-8"><title>主题切换示例</title><!-- 引入默认CSS样式 --><link rel="stylesheet" href="styles.css" id="themeStyles">
</head>
<body><header><h1>主题切换演示</h1></header><main><p>这是一个示例文本，用于展示主题切换效果。</p><button id="toggleTheme">切换主题</button></main><!-- 引入JavaScript文件 --><script src="script.js"></script>
</body>
</html>
CSS (styles.css)
css/* 默认主题样式 */
body {background-color: white;color: black;
}/* 夜间主题样式，通过类名控制 */
body.night-mode {background-color: #333;color: white;
}
JavaScript (script.js)
javascript// 获取切换主题按钮
const toggleButton = document.getElementById('toggleTheme');// 定义切换主题的函数
function toggleTheme() {// 获取当前文档的根元素，即bodyconst bodyElement = document.body;// 判断是否已应用夜间模式类名if (bodyElement.classList.contains('night-mode')) {// 如果已应用，移除它，恢复到默认主题bodyElement.classList.remove('night-mode');} else {// 如果未应用，添加夜间模式类名bodyElement.classList.add('night-mode');}
}// 绑定按钮点击事件
toggleButton.addEventListener('click', toggleTheme);

过程说明：

  1. 用户访问页面时，看到的是由styles.css定义的默认主题样式。
  2. 当用户点击“切换主题”按钮时，会触发toggleTheme函数。
  3. toggleTheme函数通过检查body元素是否具有.night-mode类来判断当前主题，并据此添加或移除该类，从而在默认主题和夜间主题之间切换。
  4. 由于CSS中已经定义了.night-mode类对应的样式，所以页面的外观会立即响应这些变化，实现主题的即时切换。

相关文章：

主题切换之根元素CSS自定义类

要实现CSS样式的主题切换&#xff0c;可以通过在HTML中添加一个按钮来触发JavaScript事件&#xff0c;进而通过JavaScript动态修改HTML元素的class或直接切换CSS文件&#xff0c;以达到改变页面整体风格的目的。以下是实现这一功能的步骤、原理及代码示例。 原理&#xff1a; …...

编程日记 2024/6/15 9:41:09

如何在 ASP.NET Core Web Api 项目中应用 NLog 写日志？

前言 昨天分享了在 .NET Core Console 项目中应用 NLog 写日志的详细例子&#xff0c;有几位小伙伴私信说 ASP.NET Core Web Api 项目中无法使用&#xff0c;其实在 ASP.NET Core Web Api 项目中应用 NLog 写日志&#xff0c;跟 .NET Core Console 项目是有些不一样的&#xf…...

编程日记 2024/6/15 9:40:06

selenium execute_script常用方法汇总

driver.execute_script() 是 Selenium WebDriver 中非常强大且灵活的功能&#xff0c;可以用来执行任意的 JavaScript 代码在浏览器上下文中。以下是一些常用的 execute_script() 方法的例子和用法&#xff1a; 修改元素的属性和值 python# 修改输入框的值 driver.execute_sc…...

编程日记 2024/6/15 9:39:03

如何选择最佳的APP封装平台-小猪APP分发为您解忧

在开发移动应用程序的过程中&#xff0c;选择一个可靠的APP封装平台显得尤为重要。无论你是初创企业还是大型企业&#xff0c;找到一个合适的平台可以大大简化你的开发流程。如何选择最佳的APP封装平台呢&#xff1f;今天我们就来聊聊这个话题&#xff0c;并重点介绍一下小猪AP…...

编程日记 2024/6/15 9:38:02

Linux基础 （十八）：Libevent 库的安装与使用

目录 一、Libevent 概述 1.0 Libevent的安装 1.0.1 使用源码方式 1.0.2 终端命令行安装 1.1 主要特性 1.2 主要组件 1.3 Libevent 使用模型 1.4 原理 1.5 使用的基本步骤 1.5.1 初始化事件基础设施 1.5.2. 创建和绑定服务器套接字 1.5.3. 设置监听事件 1.5.4. 定义…...

编程日记 2024/6/15 9:33:57

冒泡排序的详细介绍 , 以及c , python , Java的实现方法

冒泡排序&#xff08;Bubble Sort&#xff09;是一种简单的排序算法&#xff0c;它重复地遍历要排序的数列&#xff0c;一次比较两个元素&#xff0c;如果他们的顺序错误就把他们交换过来。遍历数列的工作是重复地进行直到没有再需要交换&#xff0c;也就是说该数列已经排序完成…...

编程日记 2024/6/15 9:32:55

使用llama.cpp实现LLM大模型的格式转换、量化、推理、部署

使用llama.cpp实现LLM大模型的格式转换、量化、推理、部署 概述 llama.cpp的主要目标是能够在各种硬件上实现LLM推理&#xff0c;只需最少的设置&#xff0c;并提供最先进的性能。提供1.5位、2位、3位、4位、5位、6位和8位整数量化&#xff0c;以加快推理速度并减少内存使用。…...

编程日记 2024/6/15 9:31:54

给你一个扫码支付的二维码，如何写测试用例？

前言 面试的时候&#xff0c;经常会临场出题&#xff1a;给你一个xxx, 如何测试, 或者说如何写测试用例&#xff1f;xxx可以是圆珠笔&#xff0c;水杯&#xff0c;电梯等生活中常见的场景。 那么给你一个支付的二维码&#xff0c;如何写测试用例呢&#xff1f; 二维码扫码支…...

编程日记 2024/6/15 9:29:50

计算机专业在未来的发展与抉择

目录 前言 计算机专业的发展历史 计算机专业的前景 计算机专业的挑战 如何判断自己是否适合计算机专业 计算机行业的未来发展态势 作为过来人和从业者 前言 随着2024年高考落幕&#xff0c;数百万高三学生又将面临人生中的重要抉择&#xff1a;选择大学专业。在这个关键…...

编程日记 2024/6/15 9:27:48

【Linux】基础IO——文件描述符，重定向

话接上篇&#xff1a; 1.文件描述符fd 磁盘文件 VS 内存文件&#xff1f; 当文件存储在磁盘当中时&#xff0c;我们将其称之为磁盘文件&#xff0c;而当磁盘文件被加载到内存当中后&#xff0c;我们将加载到内存当中的文件称之为内存文件。磁盘文件和内存文件之间的关系就像程…...

编程日记 2024/6/15 9:25:46

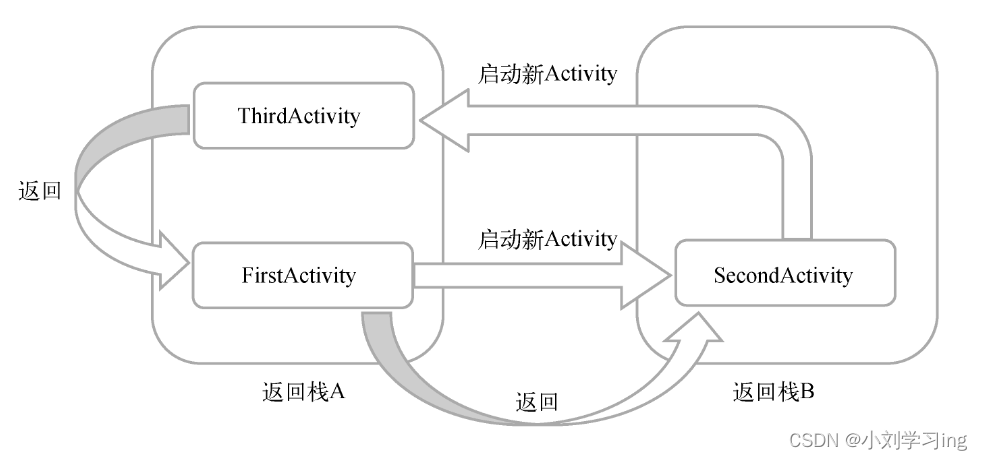
1.0 Android中Activity的基础知识

一&#xff1a;Activity的定义 Activity是一个应用组件&#xff0c;它提供了一个用户界面&#xff0c;允许用户执行一个单一的、明确的操作&#xff0c;用户看的见的操作都是在activity中执行的。Activity的实现需要在manifest中进行定义&#xff0c;不让会造成程序报错。 1.…...

编程日记 2024/6/15 9:24:45

线代知识点总结

目录 一.初等行/列变换 1.计算行列式时&#xff0c;行列变换都可 2.求矩阵的秩时&#xff0c;行列变换都可 3.解线性方程组时&#xff0c;仅能使用初等行变换 4.判定解的情况&#xff0c;单纯求r(A),r(A,b)的过程行列变换都可 5.求向量组极大无关组、线性表出关系&#x…...

编程日记 2024/6/15 9:23:43

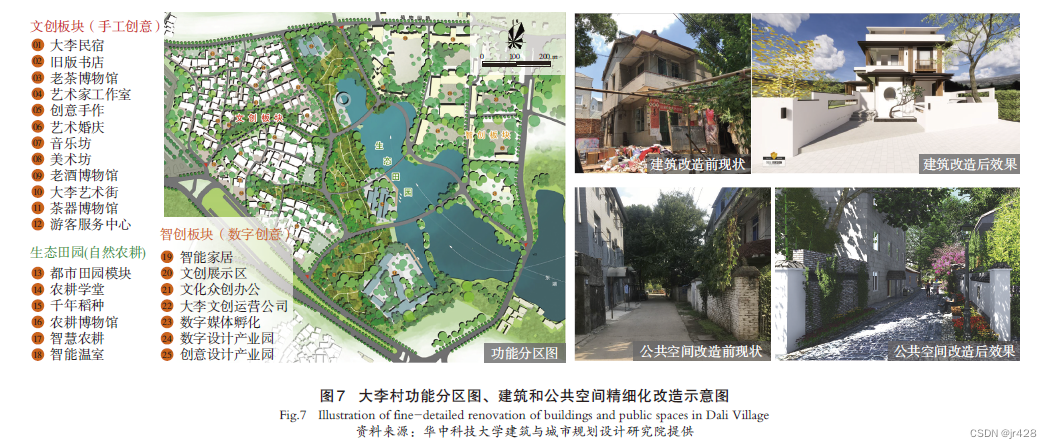
案例学习-存量更新规划实施探索（武汉）

案例学习-存量更新规划实施探索&#xff08;武汉&#xff09; 武汉市在早期旧城更新实践中发现零散化的更新往往导致资源配置分散、城市建设破碎化等弊病&#xff0c;特别是由于过于强调项目自身“经济平衡”&#xff0c;在实施过程中也逐步暴露出住宅占比过大、强度偏高、公服…...

编程日记 2024/6/15 9:22:41

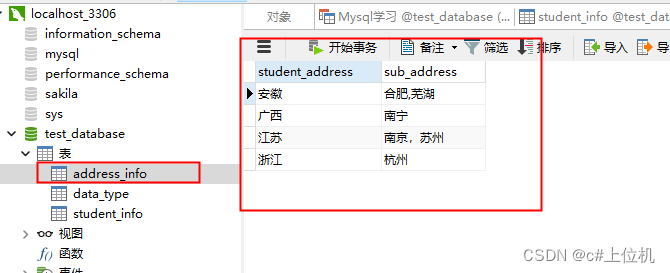
C#操作MySQL从入门到精通(17)——使用联结

前言： 我们在查询数据的过程中有时候查询的数据不是来自一个表而是来自多个表，本文使用的测试数据如下： 本文使用了两个表student_info、address_info student_info的数据如下： address_info的数据如下： 1、内联结 所谓内联结就是求交集，两个表都有的数据才是有效数…...

编程日记 2024/6/15 9:21:40

MyBatis 关于查询语句上配置的详细内容

1. MyBatis 关于查询语句上配置的详细内容 文章目录 1. MyBatis 关于查询语句上配置的详细内容2. 准备工作3. SQL查询结果&#xff0c;返回为POJO实体类型4. SQL查询结果&#xff0c;返回为List<POJO\> 集合类型5. SQL查询结果&#xff0c;返回为Map 集合6. SQL查询结果&…...

编程日记 2024/6/15 9:20:38

基于STM32和人工智能的智能家居监控系统

目录 引言环境准备智能家居监控系统基础代码实现&#xff1a;实现智能家居监控系统 4.1 数据采集模块4.2 数据处理与分析4.3 控制系统4.4 用户界面与数据可视化应用场景&#xff1a;智能家居管理与优化问题解决方案与优化收尾与总结 1. 引言 随着智能家居技术的快速发展&…...

编程日记 2024/6/15 9:19:37

这三款使用的视频、图片设计工具，提供工作效率

Videograp Videograp是一款专注于视频生成的工具&#xff0c;特别适合需要快速剪辑和编辑视频的用户。Videograp具备以下特点&#xff1a; 影音比例转换&#xff1a;Videograp支持调整视频的分辨率和比例&#xff0c;使其更适合不同的播放环境和设备。 AI快剪&#xff1a;该工…...

编程日记 2024/6/15 9:18:34

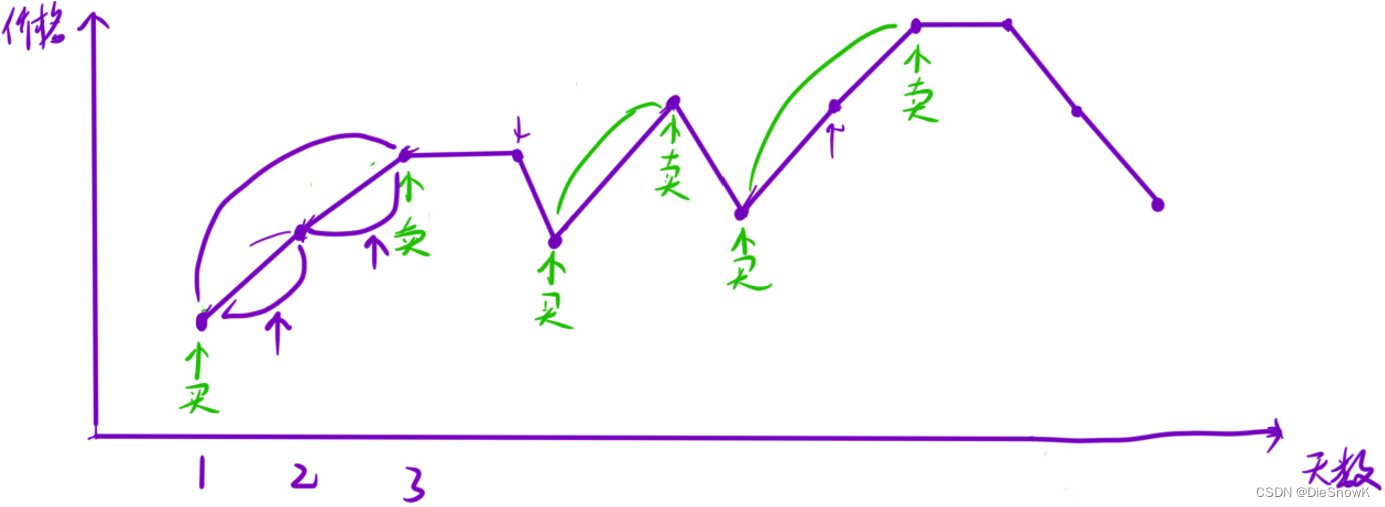
[Algorithm][贪心][最长递增子序列][递增的三元子序列][最长连续递增序列][买卖股票的最佳时机][买卖股票的最佳时机Ⅱ]详细讲解

目录 1.最长递增子序列1.题目链接2.算法原理详解3.代码实现 2.递增的三元子序列1.题目链接2.算法原理详解3.题目链接 3.最长连续递增序列1.题目链接2.算法原理详解3.代码实现 4.买卖股票的最佳时机1.题目链接2.算法原理详解3.代码实现 5.买卖股票的最佳时机 II1.题目链接2.算法…...

编程日记 2024/6/15 9:17:32

手把手教你入门vue+springboot开发（三）--登录功能后端

文章目录 前言一、redis安装二、后端代码1.修改application.yml文件2.增加utils文件3.增加Result类4.修改UserController类5.修改UserMapper类6.修改UserService和UserServiceImpl类7.增加LoginInterceptor类8.增加WebConfig类9.修改pom.xml文件 前言 前两篇我们用vuespringbo…...

编程日记 2024/6/15 9:16:31

三款有3D效果的js图表库

1、G2简洁的渐进式可视化语法。https://g2.antv.antgroup.com/manual/extra-topics/3d-charts 2、 https://www.highcharts.com/https://www.highcharts.com/ 3、https://www.fusioncharts.com/charts/pie-doughnut-charts/donut-chart-in-3d?frameworkjavascripthttps://www…...

编程日记 2024/6/15 9:14:28

Redis数据倾斜问题解决

Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中&#xff0c;部分节点存储的数据量或访问量远高于其他节点&#xff0c;导致这些节点负载过高&#xff0c;影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

编程新知 2026/1/27 19:28:11

JavaScript基础-API 和 Web API

在学习JavaScript的过程中&#xff0c;理解API&#xff08;应用程序接口&#xff09;和Web API的概念及其应用是非常重要的。这些工具极大地扩展了JavaScript的功能&#xff0c;使得开发者能够创建出功能丰富、交互性强的Web应用程序。本文将深入探讨JavaScript中的API与Web AP…...

编程新知 2025/8/21 23:03:46

在Mathematica中实现Newton-Raphson迭代的收敛时间算法（一般三次多项式）

考察一般的三次多项式&#xff0c;以r为参数&#xff1a; p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]&#xff1b; 此多项式的根为&#xff1a; 尽管看起来这个多项式是特殊的&#xff0c;其实一般的三次多项式都是可以通过线性变换化为这个形式…...

编程新知 2026/1/30 3:24:00

Razor编程中@Html的方法使用大全

文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...

编程新知 2026/1/28 4:50:33

django blank 与 null的区别

1.blank blank控制表单验证时是否允许字段为空 2.null null控制数据库层面是否为空 但是&#xff0c;要注意以下几点&#xff1a; Django的表单验证与null无关&#xff1a;null参数控制的是数据库层面字段是否可以为NULL&#xff0c;而blank参数控制的是Django表单验证时字…...

编程新知 2025/7/7 3:34:13

零知开源——STM32F103RBT6驱动 ICM20948 九轴传感器及 vofa + 上位机可视化教程

STM32F1 本教程使用零知标准板&#xff08;STM32F103RBT6&#xff09;通过I2C驱动ICM20948九轴传感器&#xff0c;实现姿态解算&#xff0c;并通过串口将数据实时发送至VOFA上位机进行3D可视化。代码基于开源库修改优化&#xff0c;适合嵌入式及物联网开发者。在基础驱动上新增…...

编程新知 2026/2/5 4:25:58

解析“道作为序位生成器”的核心原理

解析“道作为序位生成器”的核心原理 以下完整展开道函数的零点调控机制&#xff0c;重点解析"道作为序位生成器"的核心原理与实现框架&#xff1a; 一、道函数的零点调控机制 1. 道作为序位生成器 道在认知坐标系$(x_{\text{物}}, y_{\text{意}}, z_{\text{文}}…...

编程新知 2026/2/8 9:11:54

算法—栈系列

一&#xff1a;删除字符串中的所有相邻重复项 class Solution { public:string removeDuplicates(string s) {stack<char> st;for(int i 0; i < s.size(); i){char target s[i];if(!st.empty() && target st.top())st.pop();elsest.push(s[i]);}string ret…...

编程新知 2026/1/22 13:43:14

算法刷题-回溯

今天给大家分享的还是一道关于dfs回溯的问题&#xff0c;对于这类问题大家还是要多刷和总结&#xff0c;总体难度还是偏大。 对于回溯问题有几个关键点&#xff1a; 1.首先对于这类回溯可以节点可以随机选择的问题&#xff0c;要做mian函数中循环调用dfs&#xff08;i&#x…...

编程新知 2025/10/14 10:53:46

使用 uv 工具快速部署并管理 vLLM 推理环境

uv&#xff1a;现代 Python 项目管理的高效助手 uv&#xff1a;Rust 驱动的 Python 包管理新时代 在部署大语言模型&#xff08;LLM&#xff09;推理服务时&#xff0c;vLLM 是一个备受关注的方案&#xff0c;具备高吞吐、低延迟和对 OpenAI API 的良好兼容性。为了提高部署效…...

编程新知 2025/10/13 20:32:04