[Algorithm][贪心][最长递增子序列][递增的三元子序列][最长连续递增序列][买卖股票的最佳时机][买卖股票的最佳时机Ⅱ]详细讲解
目录
- 1.最长递增子序列
- 1.题目链接
- 2.算法原理详解
- 3.代码实现
- 2.递增的三元子序列
- 1.题目链接
- 2.算法原理详解
- 3.题目链接
- 3.最长连续递增序列
- 1.题目链接
- 2.算法原理详解
- 3.代码实现
- 4.买卖股票的最佳时机
- 1.题目链接
- 2.算法原理详解
- 3.代码实现
- 5.买卖股票的最佳时机 II
- 1.题目链接
- 2.算法原理详解
- 3.代码实现
1.最长递增子序列
1.题目链接
- 最长递增子序列
2.算法原理详解
-
基本思想:
- 动态规划
- 二分查找
-
动态规划思路:
- 状态表示:以
i位置的元素为结尾的所有的子序列中,最长递增子序列的长度 - 状态转移方程:
dp[i] = max(dp[j] + 1) (j < i && nums[j] < nums[i]) - 该思路中,并不关心该序列长什么样子,只在乎”最后一个元素”是谁
- 状态表示:以
-
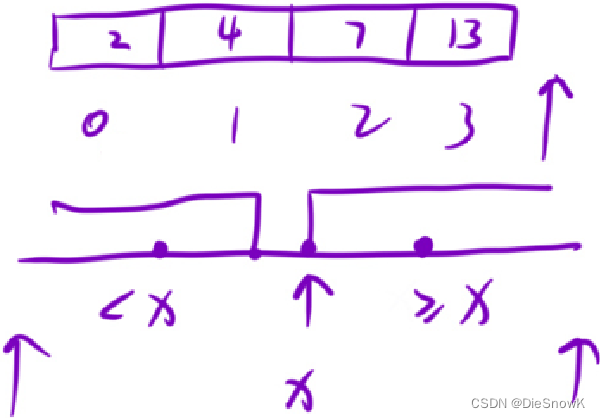
贪心优化:
- 存什么;所有长度为
x的递增子序列中,最后一个元素的最小值 - 存哪里:所有大于等于
nums[i]的最小值的位置

- 存什么;所有长度为
-
利用二分优化:时间复杂度: O ( N ) O(N) O(N) -> O ( l o g N ) O(log_N) O(logN)
3.代码实现
int lengthOfLIS(vector<int>& nums)
{int n = nums.size();vector<int> ret;ret.push_back(nums[0]);for(int i = 1; i < n; i++){if(nums[i] > ret.back()){ret.push_back(nums[i]);}else{// 二分插入位置int left = 0, right = ret.size() - 1;while(left < right){int mid = left + (right - left) / 2;if(ret[mid] < nums[i]){left = mid + 1;}else{right = mid;}}ret[left] = nums[i];}}return ret.size();
}
2.递增的三元子序列
1.题目链接
- 递增的三元子序列
2.算法原理详解
- 本题的贪心策略和最长递增子序列一样
- 但是本题只需两个变量即可完成贪心,无需数组

- 但是本题只需两个变量即可完成贪心,无需数组
3.题目链接
bool increasingTriplet(vector<int>& nums)
{int a = nums[0], b = INT_MAX;for(int i = 1; i < nums.size(); i++){if(nums[i] > b){return true;}else if(nums[i] > a){b = nums[i];}else{a = nums[i];}}return false;
}
3.最长连续递增序列
1.题目链接
- 最长连续递增序列
2.算法原理详解
- 思路;贪心 + 双指针
3.代码实现
int findLengthOfLCIS(vector<int>& nums)
{int n = nums.size(), ret = 0;for(int i = 0; i < n; ){int j = i + 1;while(j < n && nums[j - 1] < nums[j]){j++;}ret = max(ret, j - i);i = j; // 贪心}return ret;
}
4.买卖股票的最佳时机
1.题目链接
- 买卖股票的最佳时机
2.算法原理详解
- 思路:贪心 + 一个变量标记“前缀最小值”
3.代码实现
int maxProfit(vector<int>& prices)
{int ret = 0, prevMin = INT_MAX;for(int i = 0; i < prices.size(); i++){if(prices[i] > prevMin){ret = max(ret, prices[i] - prevMin);}prevMin = min(prices[i], prevMin); // 贪心}return ret;
}
5.买卖股票的最佳时机 II
1.题目链接
- 买卖股票的最佳时机 II
2.算法原理详解
-
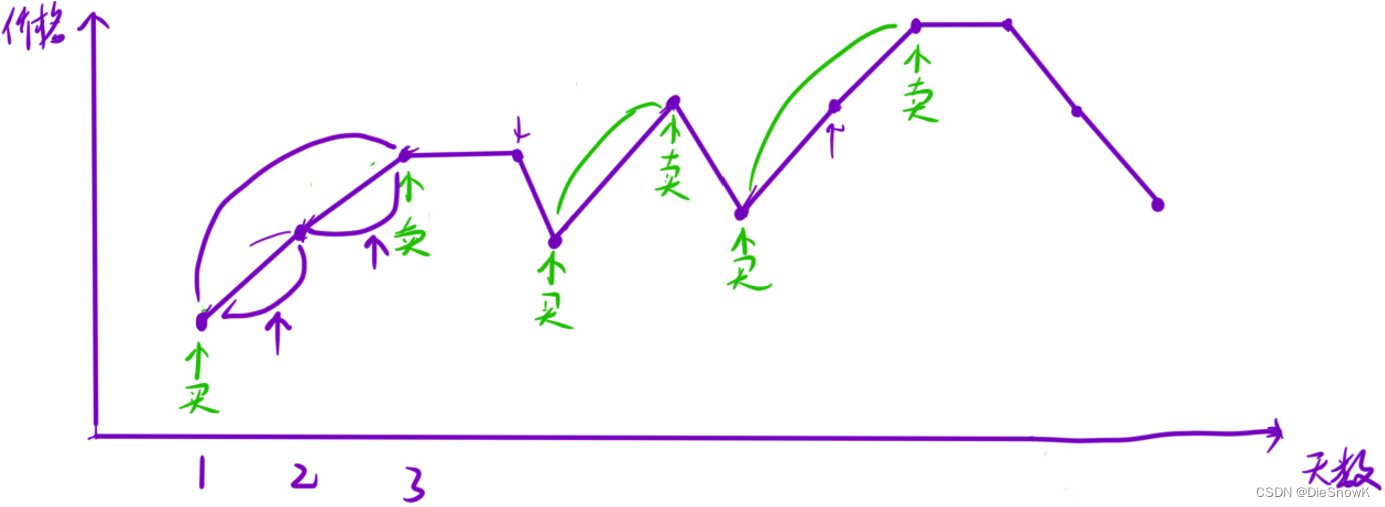
贪心:只要能获得正收益,就交易
-
实现一:双指针

-
实现二:拆分交易,把交易拆成一天一天
3.代码实现
// v1.0 双指针
int maxProfit(vector<int>& p)
{int ret = 0, n = p.size();for(int i = 0; i < n; i++){int j = i;while(j + 1 < n && p[j + 1] > p[j]){j++;}ret += p[j] - p[i];i = j;}return ret;
}
---------------------------------------------------------
// v2.0 拆分成一天一天
int maxProfit(vector<int>& p)
{int ret = 0;for(int i = 1; i < p.size(); i++){if(p[i - 1] < p[i]){ret += p[i] - p[i - 1];}}return ret;
}
相关文章:

[Algorithm][贪心][最长递增子序列][递增的三元子序列][最长连续递增序列][买卖股票的最佳时机][买卖股票的最佳时机Ⅱ]详细讲解
目录 1.最长递增子序列1.题目链接2.算法原理详解3.代码实现 2.递增的三元子序列1.题目链接2.算法原理详解3.题目链接 3.最长连续递增序列1.题目链接2.算法原理详解3.代码实现 4.买卖股票的最佳时机1.题目链接2.算法原理详解3.代码实现 5.买卖股票的最佳时机 II1.题目链接2.算法…...

手把手教你入门vue+springboot开发(三)--登录功能后端
文章目录 前言一、redis安装二、后端代码1.修改application.yml文件2.增加utils文件3.增加Result类4.修改UserController类5.修改UserMapper类6.修改UserService和UserServiceImpl类7.增加LoginInterceptor类8.增加WebConfig类9.修改pom.xml文件 前言 前两篇我们用vuespringbo…...
三款有3D效果的js图表库
1、G2简洁的渐进式可视化语法。https://g2.antv.antgroup.com/manual/extra-topics/3d-charts 2、 https://www.highcharts.com/https://www.highcharts.com/ 3、https://www.fusioncharts.com/charts/pie-doughnut-charts/donut-chart-in-3d?frameworkjavascripthttps://www…...

【SQLAlChemy】表之间的关系,外键如何使用?
表之间的关系 数据库表之间的关系分为三种: 一对一关系(One-to-One):在这种关系中,表A的每一行都与表B的一行关联,反之亦然。例如,每个人都有一个唯一的社保号,每个社保号也只属于…...

Linux 基础IO 二
1.文件描述符的分配规则 #include<stdio.h> #include<string.h> //#include<unistd.h> #include<sys/types.h> #include<sys/stat.h> #include<fcntl.h>int main() {close(1);//fd分配原则,从最小的开始,没有被占用…...

找工作小项目:day15-macOS支持、完善逻辑
macOS支持、完善逻辑 目前的代码可以在Linux上完美运行编译,在Windows上也可以通过WSL编译运行源代码,但是在MacBook上却无法运行编译,这主要是由于macOS上没有epoll,取而代之的很相似的kqueue。由于操作系统不同,我们…...
植物大战僵尸杂交版 v2.0.88 mac版 Plants vs. Zombies 杂交版下载
特别注意:该游戏最低系统要求为macOS Sonoma 14.X,低于此系统版本的请勿下载! 游戏介绍 植物大战僵尸杂交版是由B站UP主“潜艇伟伟迷”制作的一款结合了《植物大战僵尸》原有元素与创新玩法的游戏。这款游戏以其独特的“杂交”植物概念在B站…...

PHP中的while循环:用法、技巧与最佳实践
在PHP编程中,while循环是一种基本且常用的控制结构,用于重复执行代码块,直到指定条件为假。while循环在处理未知迭代次数的任务时特别有用,例如读取文件内容、处理用户输入或动态生成数据等。与for循环不同,while循环适…...

如何解决跨境传输常见的安全及效率问题?
在当今全球化的商业版图中,企业为了拓展国际市场和增强竞争力,跨境传输数据已成为一项不可或缺的业务活动。合格的数据跨境传输方案,应考虑以下要素: 法律合规性:确保方案符合所有相关国家的数据保护法律和国际法规&am…...

『大模型笔记』主成分分析(PCA)解释:简化机器学习中的复杂数据!
主成分分析(PCA)解释:简化机器学习中的复杂数据 文章目录 一. 主成分分析(PCA)解释:简化机器学习中的复杂数据!二. 参考文献一. 主成分分析(PCA)解释:简化机器学习中的复杂数据! 主成分分析(Principal Component Analysis,简称PCA)通过 将大型数据集中的维度减少…...

springboot与flowable(5):任务分配(表达式)
在做流程定义时我们需要给相关的用户节点指派对应的处理人。在flowable中提供了三种分配的方式。 一、固定分配 在分配用户时选择固定值选项确认即可。 二、表达式 1、值表达式 2、方法表达式 三、表达式流程图测试 1、导出并部署 导出流程图,复制到项目中 部署流…...
如何使用CCS9.3打开CCS3.0工程
如何使用CCS9.3打开CCS3.0工程 点菜单栏上的project,选择Import Legacy CCSv3.3 Porjects…,弹出对话框,通过Browse…按钮导入一个3.3版本的工程项目; 选择.pjt文件,选择Copy projects into worlkspace 右击选择P…...

Stable Diffusion 3 Medium 模型
开源SD3,中型版本,20亿参数,Stable Diffusion 3 Medium,系统内存要求32G,显卡6G。 a female character with long, flowing hair that appears to be made of ethereal, swirling patterns resembling the Northern Li…...
)
数据分析------统计学知识点(五)
回归算法 想象一下,你和朋友在讨论:大学生活中,每天学习的时间是否真的能影响期末成绩?这个问题看似简单,实则包含了一个潜在的关系:学习时间与成绩之间的联系。我们想要知道,增加学习时间是否会提高成绩,以及这种提…...

Superset二次开发之Git篇 git remote
背景:从GitHub clone Superset项目,基于3.0版本做二次开发,后续通过其他方式把3.0版本未做任何修改过的原始代码上传到企业GitLab库develop分支 任务:本地代码推送到GitLab库develop分支,但是两者似乎没有任何关联关系 操作步骤 克隆 Superset 3.0 版本的项目到本地: …...
记录一下PHP使用微信小程序支付
记录一下PHP使用微信小程序支付V3版本经历 官方文档:https://pay.weixin.qq.com/wiki/doc/apiv3/open/pay/chapter2_8_0.shtml 请详细查看文档中小程序支付接入前准备(https://pay.weixin.qq.com/wiki/doc/apiv3/open/pay/chapter2_8_1.shtmlÿ…...

【数据结构初阶】 --- 单链表
关于链表你应该先了解这些 下图描述了物理模型和逻辑模型,大多数常见的其实是逻辑模型,但这对初学者或者掌握不扎实的同学不太友好,所以这里我重点讲解物理模型,当了解了这些细节,以后做题或是什么就直接画逻辑模型就…...

并发、多线程、HTTP连接数有何关系?
在计算机领域,"并发"、"多线程"和"HTTP连接数"是三个重要的概念,它们之间存在着密切的关系。本文将探讨这三者之间的联系以及它们在现代计算机系统中的作用。 一、并发的概念 并发是指系统能够同时处理多个任务或事件的能…...

鸿蒙轻内核Kconfig使用笔记
鸿蒙轻内核使用Kconfig进行图形化配置,本文专门讲解下鸿蒙轻内核LiteOS-M和LiteOS-A的图形化配置方法。本文中所涉及的源码,均可以在开源站点 https://gitee.com/openharmony/kernel_liteos_a 、 https://gitee.com/openharmony/kernel_liteos_m 获取。本…...
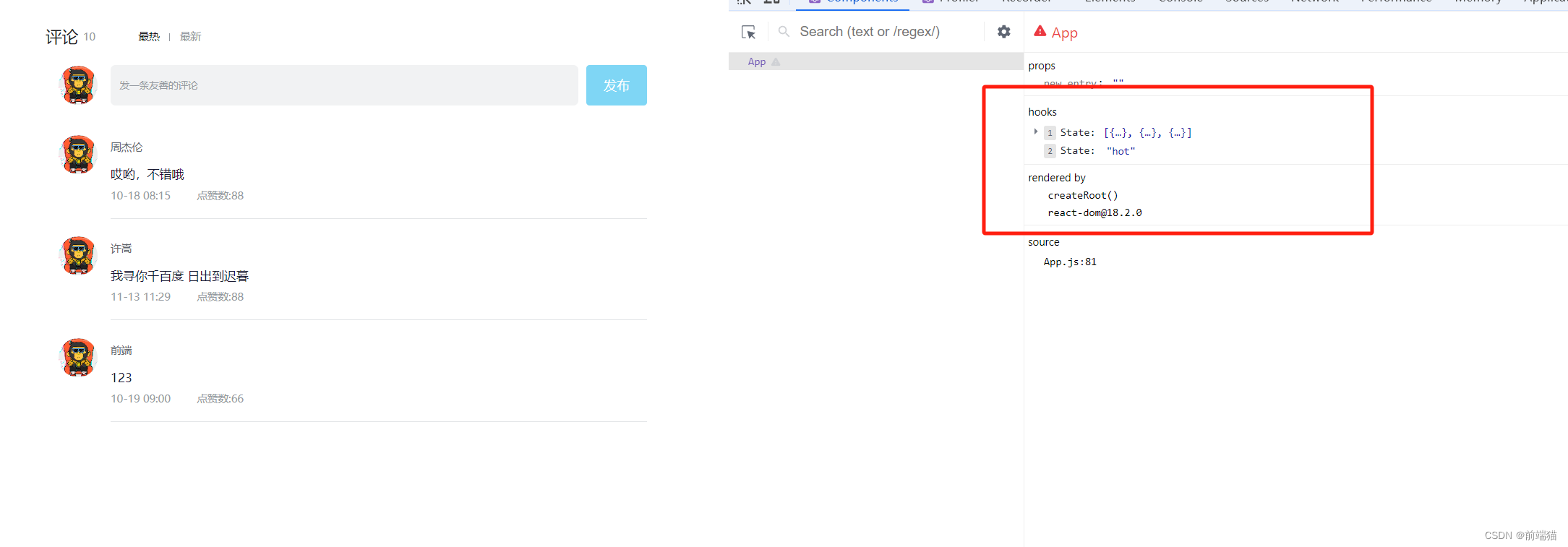
react 0至1 案例
/*** 导航 Tab 的渲染和操作** 1. 渲染导航 Tab 和高亮* 2. 评论列表排序* 最热 > 喜欢数量降序* 最新 > 创建时间降序* 1.点击记录当前type* 2.通过记录type和当前list中的type 匹配*/ import ./App.scss import avatar from ./images/bozai.png import {useState} …...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...

苹果AI眼镜:从“工具”到“社交姿态”的范式革命——重新定义AI交互入口的未来机会
在2025年的AI硬件浪潮中,苹果AI眼镜(Apple Glasses)正在引发一场关于“人机交互形态”的深度思考。它并非简单地替代AirPods或Apple Watch,而是开辟了一个全新的、日常可接受的AI入口。其核心价值不在于功能的堆叠,而在于如何通过形态设计打破社交壁垒,成为用户“全天佩戴…...

CVPR2025重磅突破:AnomalyAny框架实现单样本生成逼真异常数据,破解视觉检测瓶颈!
本文介绍了一种名为AnomalyAny的创新框架,该方法利用Stable Diffusion的强大生成能力,仅需单个正常样本和文本描述,即可生成逼真且多样化的异常样本,有效解决了视觉异常检测中异常样本稀缺的难题,为工业质检、医疗影像…...

Python 高效图像帧提取与视频编码:实战指南
Python 高效图像帧提取与视频编码:实战指南 在音视频处理领域,图像帧提取与视频编码是基础但极具挑战性的任务。Python 结合强大的第三方库(如 OpenCV、FFmpeg、PyAV),可以高效处理视频流,实现快速帧提取、压缩编码等关键功能。本文将深入介绍如何优化这些流程,提高处理…...

GeoServer发布PostgreSQL图层后WFS查询无主键字段
在使用 GeoServer(版本 2.22.2) 发布 PostgreSQL(PostGIS)中的表为地图服务时,常常会遇到一个小问题: WFS 查询中,主键字段(如 id)莫名其妙地消失了! 即使你在…...
