【逻辑回归】和【线性回归】的区别和联系-九五小庞
逻辑回归(Logistic Regression)和线性回归(Linear Regression)是两种常用的统计学习和机器学习技术,它们各自具有特定的应用场景和优势。以下是它们之间的主要区别和联系:
- 定义与目的
线性回归:是一种利用数理统计中回归分析的方法,用于确定两种或两种以上变量间相互依赖的定量关系。它的主要目的是预测连续型变量(如房价、股票价格等)。
逻辑回归:是一种广义的线性回归分析模型,主要用于解决分类问题。它通过sigmoid函数将线性回归的输出映射到0和1之间,表示某个事件发生的概率。逻辑回归常用于预测离散型变量(如疾病发生与否、贷款违约与否等)。 - 公式与计算
线性回归:其公式通常为 (y = w’x + b),其中 (w) 和 (b) 是待求参数,通过最小二乘法求解。
逻辑回归:其公式可以表示为 (p = \frac{1}{1 + e^{-(w’x + b)}}),其中 § 表示事件发生的概率,同样通过优化算法(如梯度下降)求解参数 (w) 和 (b)。 - 应用场景
线性回归:广泛应用于经济学、金融、市场营销、医学、社会科学、环境科学、工程、计算机科学、运输规划、教育研究等领域。
逻辑回归:常用于数据挖掘、疾病自动诊断、经济预测、金融风险评估、市场营销分析、社交媒体推荐、互联网广告等领域。 - 特点与要求
线性回归:
要求变量服从正态分布。
要求因变量是连续性数值变量。
要求自变量和因变量呈线性关系。
逻辑回归:
对变量分布没有要求。
要求因变量是分类型变量(通常是二分类)。
不要求自变量和因变量呈线性关系。 - 联系
逻辑回归可以看作是在线性回归的基础上,通过sigmoid函数将输出映射到概率值,从而解决了分类问题。从某种意义上说,逻辑回归是线性回归的一种扩展或变种。
总结
逻辑回归和线性回归各有其独特的应用场景和优势。线性回归适用于预测连续型变量,而逻辑回归则更擅长处理分类问题。在选择使用哪种方法时,需要根据实际问题的性质和数据的特点来决定。
相关文章:

【逻辑回归】和【线性回归】的区别和联系-九五小庞
逻辑回归(Logistic Regression)和线性回归(Linear Regression)是两种常用的统计学习和机器学习技术,它们各自具有特定的应用场景和优势。以下是它们之间的主要区别和联系: 定义与目的 线性回归:…...

富格林:正视欺诈阻挠交易被骗
富格林指出,在交易的过程中,投资者们就算做了十分的把握,也难免会出现亏损。因此建议新手投资者,在准备投资时一定要做好充分的准备工作,明辨欺诈陷阱,同时学习正规的做单盈利技巧,这才能帮助我…...

如何在WPS中加载EndNote X9插件
如何在WPS中加载EndNote X9插件 步骤1:关闭WPS 确保所有WPS文档和窗口都已关闭。 步骤2:修改文件后缀 打开文件资源管理器,导航到路径:C:\Program Files (x86)\EndNote X9\Product-Support\CWYW。找到文件 Cwyw_X86.dat&#…...
vb.net小demo(计算器、文件处理等/C#也可看)
Demo1:使用窗体控件实现一个简易版计算器 Public Class Form1Private Sub Button_1_Click(sender As Object, e As EventArgs) Handles Button_1.ClickCalSubBox.Text Button_1.TextEnd SubPrivate Sub Button_2_Click(sender As Object, e As EventArgs) Handles …...

【vue3|第8期】深入理解Vue 3 computed计算属性
日期:2024年6月10日 作者:Commas 签名:(ง •_•)ง 积跬步以致千里,积小流以成江海…… 注释:如果您觉得有所帮助,帮忙点个赞,也可以关注我,我们一起成长;如果有不对的地方…...
《精通ChatGPT:从入门到大师的Prompt指南》附录C:专业术语表
附录C:专业术语表 本附录旨在为读者提供一本全面的术语表,帮助理解《精通ChatGPT:从入门到大师的Prompt指南》中涉及的各种专业术语。无论是初学者还是高级用户,这些术语的定义和解释将为您在使用ChatGPT时提供重要参考。 A AI&…...
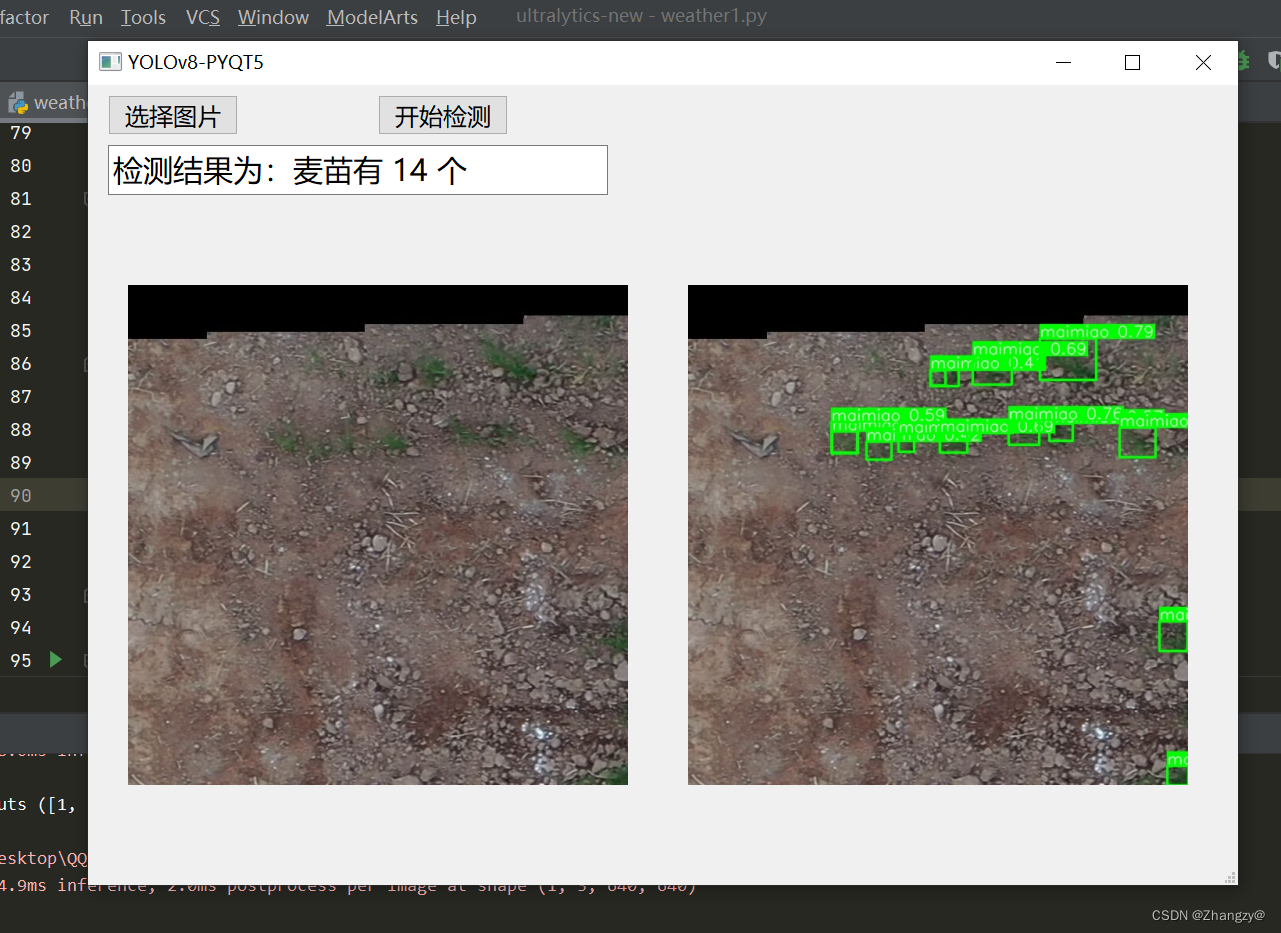
YOLOv8可视化界面PYQT5
yolov8,可视化界面pyqt。支持图片检测,视频检测,摄像头检测等,实时显示检测画面。支持自定义数据集,计数,fps展示……,即插即用,无需更改太多代码...

远程代码执行和远程命令执行是一个东西吗
远程代码执行(Remote Code Execution,简称RCE)和远程命令执行在概念上有所区别,但两者都涉及到攻击者通过远程方式在目标系统上执行代码或命令。以下是两者的详细比较: 定义: 远程代码执行(RCE…...

C++ 20新特性之线程与jthread
💡 如果想阅读最新的文章,或者有技术问题需要交流和沟通,可搜索并关注微信公众号“希望睿智”。 为什么要引入jthread 在C 11中,已经引入了std::thread。std::thread为C标准库带来了一流的线程支持,极大地促进了多线程…...
)
赶紧收藏!2024 年最常见 20道并发编程面试题(七)
上一篇地址:赶紧收藏!2024 年最常见 20道并发编程面试题(六)-CSDN博客 十三、什么是线程局部存储(Thread-Local Storage)? 线程局部存储(Thread-Local Storage,简称TLS…...
HAL库开发--第一盏灯
知不足而奋进 望远山而前行 目录 文章目录 前言 学习目标 学习内容 需求 开发流程 项目创建 芯片配置 功能配置 时钟配置 项目配置 编写代码 编译测试 烧录失败解决 编辑 总结 前言 在嵌入式系统开发中,掌握HAL库开发流程、STMCubeMX配置过程以及…...
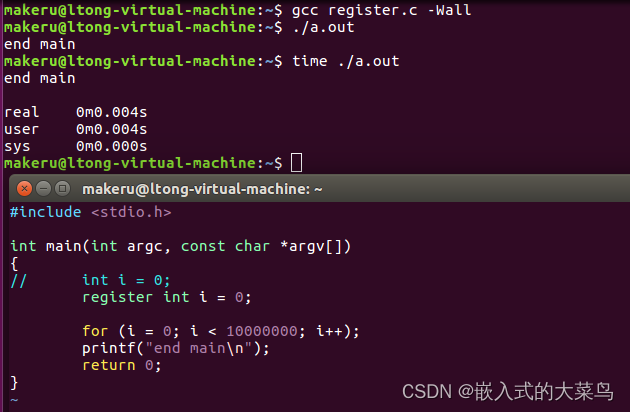
Linux C语言:变量的作用域和生命周期(auto、register、static和extern)
一、变量存储类型-auto 1、auto变量的说明 变量在程序中使用时,必须预先说明它们的存储类型和数据类型。 变量说明的一般形式是: <存储类型> <数据类型 > <变量名> ; <存储类型>是关键词auto、register、static和extern<…...

AI Stable diffusion 报错:稳定扩散模型加载失败,退出
可能是内存不够,看看你最近是加了新的大的模型,可以把你的stable-diffusion-webui\models\Stable-diffusion目录下的某个ckpt删除掉,可能ckpt太大,无法加载成功; Stable diffusion model failed to load, exiting 如图…...
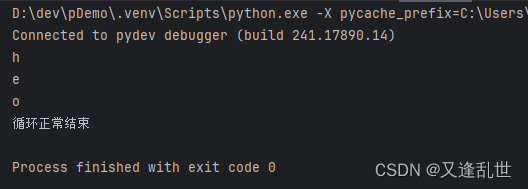
[Python学习篇] Python循环语句
while 循环 语法: while 条件: 条件成立后会重复执行的代码 ...... 示例1:死循环 # 这是一个死循环示例 while True:print("我正在重复执行")示例2:循环指定次数 i 1 while i < 5:print(f"执行次数 {i}")…...

MongoDB 正则表达式
MongoDB 正则表达式 MongoDB 是一个流行的 NoSQL 数据库,它提供了强大的查询功能,包括对正则表达式的支持。正则表达式是一种强大的文本搜索工具,它允许用户根据特定的模式匹配和搜索字符串。在 MongoDB 中,正则表达式可以用于查…...
Django配置连接池:使用django-db-connection-pool配置连接池
一、该三方库文档使用 github地址: https://github.com/altairbow/django-db-connection-pool/blob/1.2.5/README_CN.mdhttps://github.com/altairbow/django-db-connection-pool/blob/1.2.5/README_CN.md1、选择指定版本,查看指定版本的文档和配置&am…...
SpringBoot整合钉钉实现消息推送
前言 钉钉作为一款企业级通讯工具,具有广泛的应用场景,包括但不限于团队协作、任务提醒、工作汇报等。 通过Spring Boot应用程序整合钉钉实现消息推送,我们可以实现以下功能: 实时向指定用户或群组发送消息通知。自定义消息内容…...
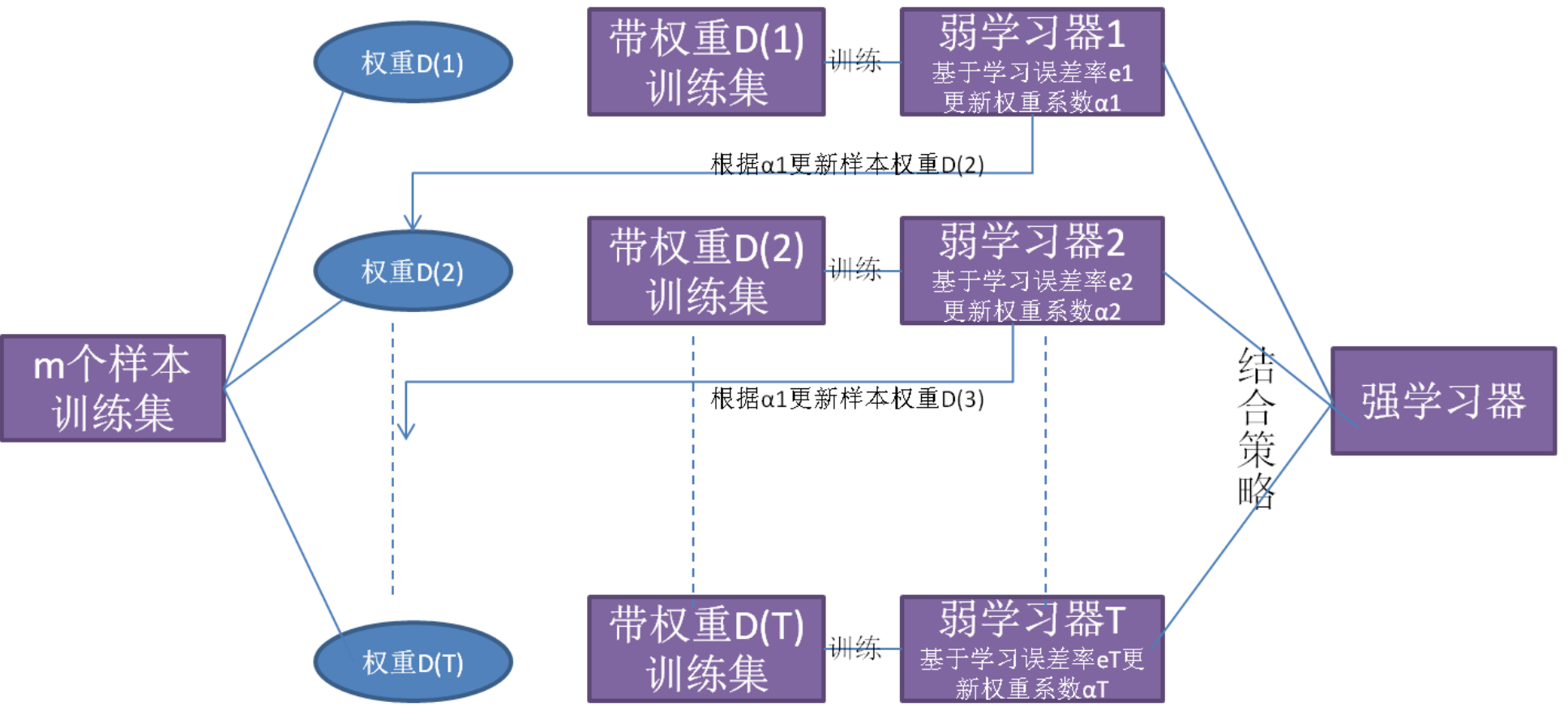
【机器学习】集成学习方法:Bagging与Boosting的应用与优势
🔥 个人主页:空白诗 文章目录 引言一、集成学习的定义二、Bagging方法1. 随机森林(Random Forest)2. 其他Bagging方法 二、Boosting方法1. 梯度提升树(Gradient Boosting Machine, GBM)解释GBM的基本原理和…...
工业 web4.0 的 UI 卓越非凡
工业 web4.0 的 UI 卓越非凡...
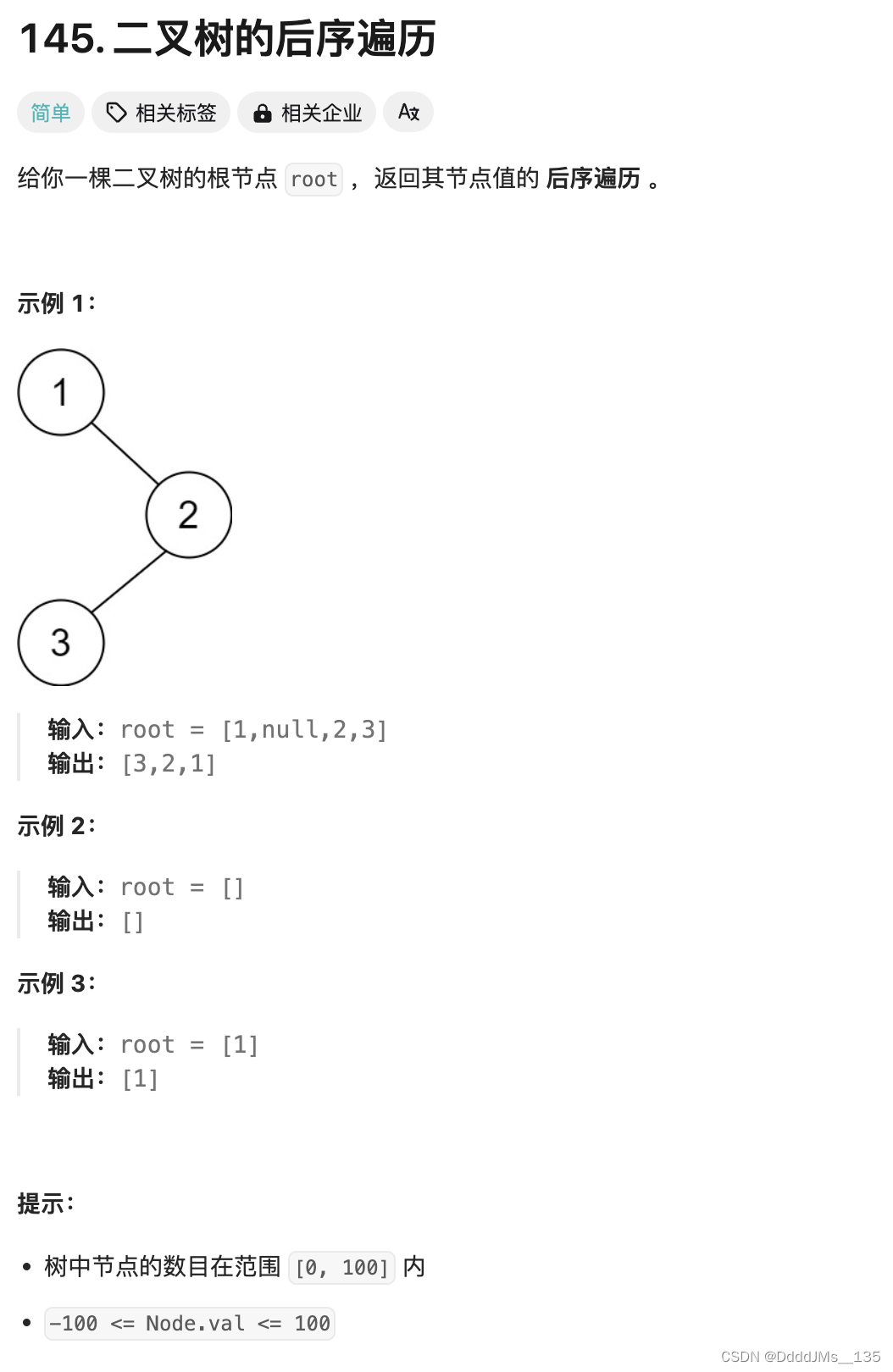
C语言 | Leetcode C语言题解之第145题二叉树的后序遍历
题目: 题解: void addPath(int *vec, int *vecSize, struct TreeNode *node) {int count 0;while (node ! NULL) {count;vec[(*vecSize)] node->val;node node->right;}for (int i (*vecSize) - count, j (*vecSize) - 1; i < j; i, --j)…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...

AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

stm32wle5 lpuart DMA数据不接收
配置波特率9600时,需要使用外部低速晶振...

Modbus RTU与Modbus TCP详解指南
目录 1. Modbus协议基础 1.1 什么是Modbus? 1.2 Modbus协议历史 1.3 Modbus协议族 1.4 Modbus通信模型 🎭 主从架构 🔄 请求响应模式 2. Modbus RTU详解 2.1 RTU是什么? 2.2 RTU物理层 🔌 连接方式 ⚡ 通信参数 2.3 RTU数据帧格式 📦 帧结构详解 🔍…...

软件工程 期末复习
瀑布模型:计划 螺旋模型:风险低 原型模型: 用户反馈 喷泉模型:代码复用 高内聚 低耦合:模块内部功能紧密 模块之间依赖程度小 高内聚:指的是一个模块内部的功能应该紧密相关。换句话说,一个模块应当只实现单一的功能…...
