【CS.AL】算法核心之分治算法:从入门到进阶
文章目录
- 1. 概述
- 2. 适用场景
- 3. 设计步骤
- 4. 优缺点
- 5. 典型应用
- 6. 题目和代码示例
- 6.1 简单题目:归并排序
- 6.2 中等题目:最近点对问题
- 6.3 困难题目:分数背包问题
- 7. 题目和思路表格
- 8. 总结
- References
1000.01.CS.AL.1.4-核心-DivedeToConquerAlgorithm-Created: 2024-06-15.Saturday09:35
1. 概述
分治算法(Divide and Conquer)是一种重要的算法设计思想,其核心思想是将一个复杂的问题分解为多个相对简单的小问题,通过解决这些小问题再合并其结果,从而得到原问题的解。分治算法的典型特征是递归,常用于求解具有重复子问题性质的问题。
2. 适用场景
分治算法适用于以下场景:
- 问题可以分解为若干个规模较小且相互独立的子问题。
- 这些子问题的解可以合并得到原问题的解。
- 具有最优子结构性质,即子问题的最优解可以合成原问题的最优解。
3. 设计步骤
- 分解(Divide):将原问题分解为若干个子问题,这些子问题的结构与原问题相同但规模较小。
- 解决(Conquer):递归地解决这些子问题。当子问题的规模足够小时,直接解决。
- 合并(Combine):将子问题的解合并,得到原问题的解。
4. 优缺点
- 优点:分治算法的递归思想使其在解决许多复杂问题时表现出色。具有良好的可扩展性和并行计算的潜力。
- 缺点:对于某些问题,分治算法可能会引入额外的开销,如递归调用栈和合并步骤的时间复杂度。
5. 典型应用
- 归并排序(Merge Sort):一种高效的排序算法,利用分治思想将数组分为两半,递归地排序并合并。
- 快速排序(Quick Sort):另一种高效的排序算法,选择一个基准元素,将数组分为两部分,递归排序。
- 最近点对问题(Closest Pair Problem):在平面上找到距离最近的两点,分治法可以将时间复杂度降至 O(nlogn)O(n \log n)O(nlogn)。
- 矩阵乘法(Strassen’s Algorithm):一种用于矩阵乘法的分治算法,降低了时间复杂度。
6. 题目和代码示例
6.1 简单题目:归并排序
题目描述:实现归并排序算法,对给定的数组进行排序。
代码示例:
#include <iostream>
#include <vector>// 函数声明
void mergeSort(std::vector<int>& arr, int left, int right);
void merge(std::vector<int>& arr, int left, int mid, int right);int main() {std::vector<int> arr = {38, 27, 43, 3, 9, 82, 10};mergeSort(arr, 0, arr.size() - 1);for (int num : arr) {std::cout << num << " ";}std::cout << std::endl;return 0;
}// 归并排序:递归地将数组分成两半进行排序
void mergeSort(std::vector<int>& arr, int left, int right) {if (left < right) {int mid = left + (right - left) / 2;mergeSort(arr, left, mid);mergeSort(arr, mid + 1, right);merge(arr, left, mid, right);}
}// 合并两个已排序的子数组
void merge(std::vector<int>& arr, int left, int mid, int right) {int n1 = mid - left + 1;int n2 = right - mid;std::vector<int> L(n1), R(n2);for (int i = 0; i < n1; ++i) {L[i] = arr[left + i];}for (int j = 0; j < n2; ++j) {R[j] = arr[mid + 1 + j];}int i = 0, j = 0, k = left;while (i < n1 && j < n2) {if (L[i] <= R[j]) {arr[k] = L[i++];} else {arr[k] = R[j++];}++k;}while (i < n1) {arr[k++] = L[i++];}while (j < n2) {arr[k++] = R[j++];}
}Others.
def merge_sort(arr):if len(arr) > 1:mid = len(arr) // 2left_half = arr[:mid]right_half = arr[mid:]merge_sort(left_half)merge_sort(right_half)i = j = k = 0while i < len(left_half) and j < len(right_half):if left_half[i] < right_half[j]:arr[k] = left_half[i]i += 1else:arr[k] = right_half[j]j += 1k += 1while i < len(left_half):arr[k] = left_half[i]i += 1k += 1while j < len(right_half):arr[k] = right_half[j]j += 1k += 1# 示例
arr = [38, 27, 43, 3, 9, 82, 10]
merge_sort(arr)
print(arr) # 输出: [3, 9, 10, 27, 38, 43, 82]
6.2 中等题目:最近点对问题
题目描述:在平面上找到距离最近的两点,时间复杂度为 O(nlogn)。
代码示例:
#include <iostream>
#include <vector>
#include <cmath>
#include <algorithm>struct Point {int x, y;
};double dist(const Point& p1, const Point& p2) {return std::sqrt((p1.x - p2.x) * (p1.x - p2.x) + (p1.y - p2.y) * (p1.y - p2.y));
}double closestPair(std::vector<Point>& points, int left, int right) {if (right - left <= 3) {double minDist = std::numeric_limits<double>::infinity();for (int i = left; i < right; ++i) {for (int j = i + 1; j <= right; ++j) {minDist = std::min(minDist, dist(points[i], points[j]));}}return minDist;}int mid = left + (right - left) / 2;double d1 = closestPair(points, left, mid);double d2 = closestPair(points, mid + 1, right);double d = std::min(d1, d2);std::vector<Point> strip;for (int i = left; i <= right; ++i) {if (std::abs(points[i].x - points[mid].x) < d) {strip.push_back(points[i]);}}std::sort(strip.begin(), strip.end(), [](const Point& p1, const Point& p2) {return p1.y < p2.y;});double minDist = d;for (size_t i = 0; i < strip.size(); ++i) {for (size_t j = i + 1; j < strip.size() && (strip[j].y - strip[i].y) < minDist; ++j) {minDist = std::min(minDist, dist(strip[i], strip[j]));}}return minDist;
}int main() {std::vector<Point> points = {{2, 3}, {12, 30}, {40, 50}, {5, 1}, {12, 10}, {3, 4}};std::sort(points.begin(), points.end(), [](const Point& p1, const Point& p2) {return p1.x < p2.x;});std::cout << "最近点对距离: " << closestPair(points, 0, points.size() - 1) << std::endl;return 0;
}
Others.
import mathdef dist(p1, p2):return math.sqrt((p1[0] - p2[0]) ** 2 + (p1[1] - p2[1]) ** 2)def closest_pair(points):def closest_pair_recursive(points):if len(points) <= 3:return min((dist(p1, p2), (p1, p2)) for i, p1 in enumerate(points) for p2 in points[i+1:])[1]mid = len(points) // 2left_half = points[:mid]right_half = points[mid:](d1, pair1) = closest_pair_recursive(left_half)(d2, pair2) = closest_pair_recursive(right_half)d = min(d1, d2)pair = pair1 if d1 < d2 else pair2strip = [p for p in points if abs(p[0] - points[mid][0]) < d]strip.sort(key=lambda p: p[1])for i in range(len(strip)):for j in range(i+1, len(strip)):if strip[j][1] - strip[i][1] >= d:breakd_new = dist(strip[i], strip[j])if d_new < d:d = d_newpair = (strip[i], strip[j])return d, pairpoints.sort(key=lambda p: p[0])return closest_pair_recursive(points)[1]# 示例
points = [(2, 3), (12, 30), (40, 50), (5, 1), (12, 10), (3, 4)]
print(closest_pair(points)) # 输出: ((2, 3), (3, 4))
6.3 困难题目:分数背包问题
题目描述:给定物品的重量和价值,求在背包容量限制下的最大价值,物品可以分割。
代码示例:
#include <iostream>
#include <vector>
#include <algorithm>struct Item {double value;double weight;
};double fractionalKnapsack(std::vector<Item>& items, double capacity) {std::sort(items.begin(), items.end(), [](const Item& a, const Item& b) {return (a.value / a.weight) > (b.value / b.weight);});double totalValue = 0;for (const auto& item : items) {if (capacity >= item.weight) {capacity -= item.weight;totalValue += item.value;} else {totalValue += item.value * (capacity / item.weight);break;}}return totalValue;
}int main() {std::vector<Item> items = {{60, 10}, {100, 20}, {120, 30}};double capacity = 50;std::cout << "背包的最大价值: " << fractionalKnapsack(items, capacity) << std::endl;return 0;
}
Others.
def fractional_knapsack(values, weights, capacity):items = list(zip(values, weights))items.sort(key=lambda x: x[0] / x[1], reverse=True)total_value = 0for value, weight in items:if capacity >= weight:capacity -= weighttotal_value += valueelse:total_value += value * (capacity / weight)breakreturn total_value# 示例
values = [60, 100, 120]
weights = [10, 20, 30]
capacity = 50
print(fractional_knapsack(values, weights, capacity)) # 输出: 240.0
7. 题目和思路表格
| 序号 | 题目 | 题目描述 | 分治策略 | 代码实现 |
|---|---|---|---|---|
| 1 | 归并排序 | 对给定的数组进行排序 | 递归地将数组分成两半进行排序 | 代码 |
| 2 | 最近点对问题 | 找到距离最近的两点 | 将点集合递归地分成两半 | 代码 |
| 3 | 分数背包问题 | 求在背包容量限制下的最大价值 | 每次选择单位重量价值最高的物品 | 代码 |
| 4 | 快速排序 | 高效排序算法 | 选择一个基准元素,将数组分为两部分,递归排序 | 代码 |
| 5 | 矩阵乘法 | 用于矩阵乘法 | 将矩阵分成更小的子矩阵,递归计算 | - |
| 6 | 求逆序对数量 | 统计数组中的逆序对个数 | 使用分治法将数组分成两半,递归统计逆序对 | - |
| 7 | 最大子序和 | 找出最大和的连续子序列 | 将序列递归地分成两半,合并子序列的结果 | - |
| 8 | 大整数乘法 | 实现高效的大整数乘法 | 使用Karatsuba算法,将大整数分成两部分进行递归计算 | - |
| 9 | 二维平面上的最近点对 | 在平面上找到距离最近的两点 | 将点集合递归地分成两半,合并结果 | - |
| 10 | 棋盘覆盖问题 | 用L型骨牌覆盖2^n * 2^n的棋盘 | 将棋盘递归地分成四部分,覆盖部分棋盘 | - |
8. 总结
分治算法是一种强大的算法设计思想,能够高效地解决许多复杂的问题。通过将问题分解为更小的子问题,分治算法不仅能够降低时间复杂度,还具有良好的可扩展性。在实际应用中,理解和掌握分治算法的思想和典型应用,对于解决各种问题具有重要意义。通过本文的例子和思路,相信读者能够深入理解分治算法的关键概念,并灵活应用于实际问题中。
References
相关文章:

【CS.AL】算法核心之分治算法:从入门到进阶
文章目录 1. 概述2. 适用场景3. 设计步骤4. 优缺点5. 典型应用6. 题目和代码示例6.1 简单题目:归并排序6.2 中等题目:最近点对问题6.3 困难题目:分数背包问题 7. 题目和思路表格8. 总结References 1000.01.CS.AL.1.4-核心-DivedeToConquerAlg…...

leetcode刷题记录:hot100强化训练2:二叉树+图论
二叉树 36. 二叉树的中序遍历 递归就不写了,写一下迭代法 class Solution(object):def inorderTraversal(self, root):""":type root: TreeNode:rtype: List[int]"""if not root:return res []cur rootstack []while cur or st…...
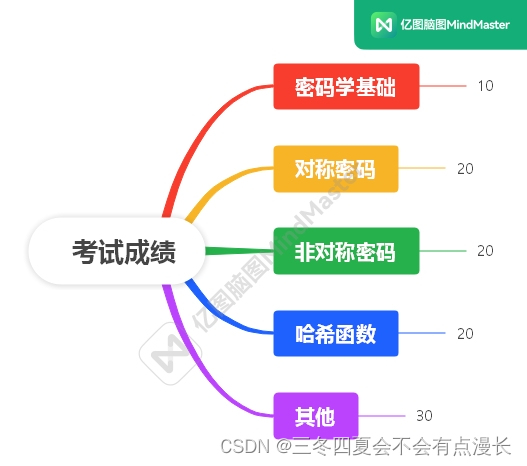
湘潭大学信息与网络安全复习笔记2(总览)
前面的实验和作业反正已经结束了,现在就是集中火力把剩下的内容复习一遍,这一篇博客的内容主要是参考教学大纲和教学日历 文章目录 教学日历教学大纲 教学日历 总共 12 次课,第一次课是概述,第二次和第三次课是密码学基础&#x…...

C语言:头歌使用函数找出数组中的最大值
任务描述 本关任务:本题要求实现一个找出整型数组中最大值的函数。 函数接口定义: int FindArrayMax( int a[], int n ); 其中a是用户传入的数组,n是数组a中元素的个数。函数返回数组a中的最大值。 主程序样例: #include <stdio.h>#…...

【技巧】Leetcode 191. 位1的个数【简单】
位1的个数 编写一个函数,输入是一个无符号整数(以二进制串的形式),返回其二进制表达式中 设置位 的个数(也被称为汉明重量)。 示例 1: 输入:n 11 输出:3 解释&#x…...

【Pandas驯化-02】pd.read_csv读取中文出现error解决方法
【Pandas】驯化-02pd.read_csv读取中文出现error解决方法 本次修炼方法请往下查看 🌈 欢迎莅临我的个人主页 👈这里是我工作、学习、实践 IT领域、真诚分享 踩坑集合,智慧小天地! 🎇 相关内容文档获取 微信公众号 &…...
)
linux下C语言如何操作文件(三)
我们继续介绍file_util.c中的函数: bool create_dir(const char* path):创建目录,根据给定的path创建目录,成功返回true,否则返回false。如果有父目录不存在,该函数不会创建。 /*** 创建目录* @param path 目录路径* @return true 创建成功,false 创建失败*/ bool cre…...
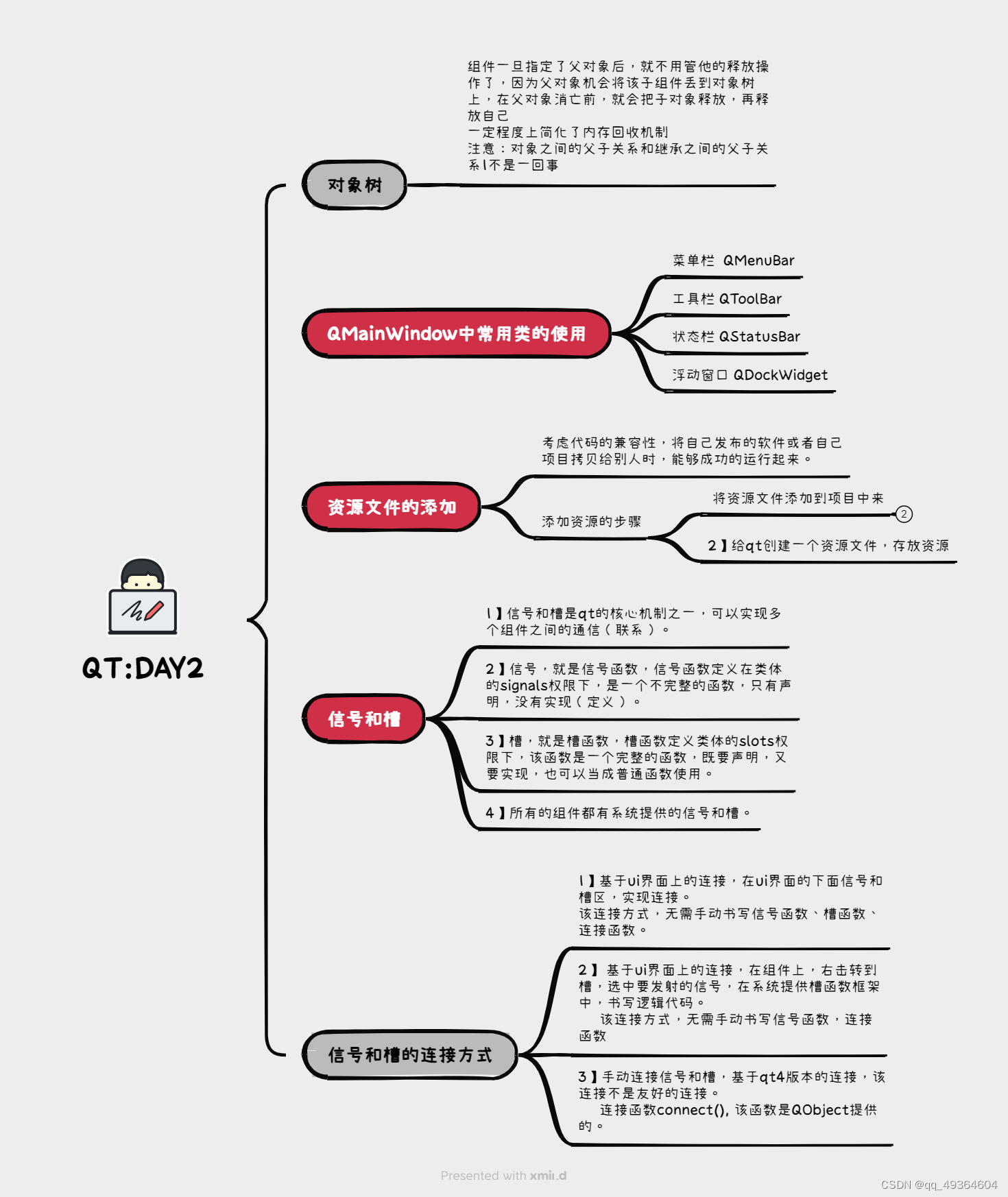
6.14作业
使用手动连接,将登录框中的取消按钮使用第二中连接方式,右击转到槽,在该槽函数中,调用关闭函数 将登录按钮使用qt4版本的连接到自定义的槽函数中,在槽函数中判断ui界面上输入的账号是否为"admin"࿰…...
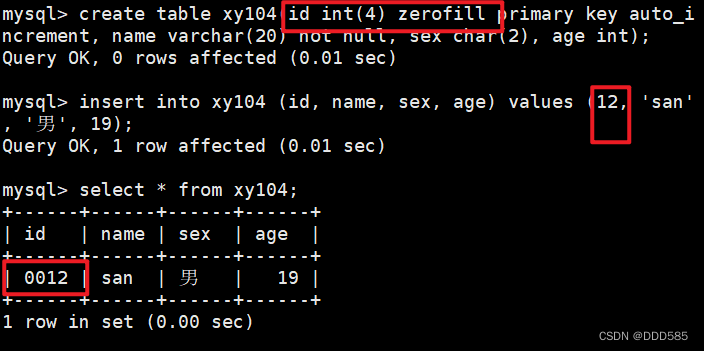
MySQL数据库管理(一)
目录 1.MySQL数据库管理 1.1 常用的数据类型编辑 1.2 char和varchar区别 2. 增删改查命令操作 2.1 查看数据库结构 2.2 SQL语言 2.3 创建及删除数据库和表 2.4 管理表中的数据记录 2.5 修改表名和表结构 3.MySQL的6大约束属性 1.MySQL数据库管理 1.1 常用的数据类…...

Kafka使用教程和案例详解
Kafka 使用教程和案例详解 Kafka 使用教程和案例详解1. Kafka 基本概念1.1 Kafka 是什么?1.2 核心组件2. Kafka 安装与配置2.1 安装 Kafka使用包管理器(如 yum)安装使用 Docker 安装2.2 配置 Kafka2.3 启动 Kafka3. Kafka 使用教程3.1 创建主题3.2 生产消息3.3 消费消息3.4 …...

TGI模型- 同期群-评论文本
用户偏好分析 TGI 1.1 用户偏好分析介绍 要分析的目标,在目标群体中的均值 和 全部群体里的均值进行比较, 差的越多说明 目标群体偏好越明显 TGI(Target Group Index,目标群体指数)用于反映目标群体在特定研究范围内…...
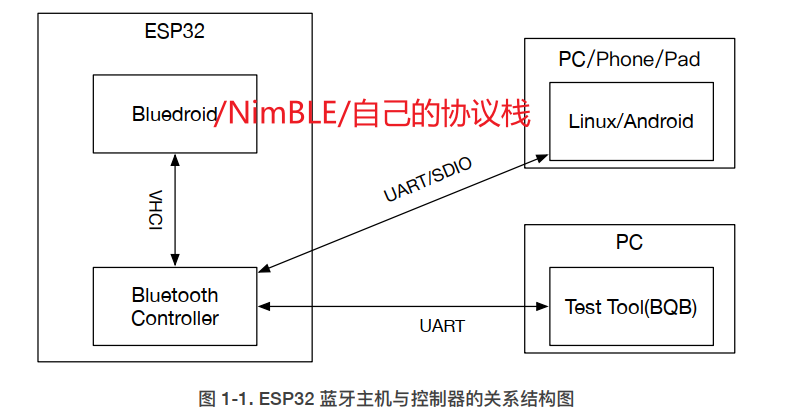
ESP32 BLE学习(0) — 基础架构
前言 (1)学习本文之前,需要先了解一下蓝牙的基本概念:BLE学习笔记(0.0) —— 基础概念(0) (2) 学习一款芯片的蓝牙肯定需要先简单了解一下该芯片的体系结构&a…...

【JAVA】Java中Spring Boot如何设置全局的BusinessException
文章目录 前言一、函数解释二、代码实现三、总结 前言 在Java应用开发中,我们常常需要读取配置文件。Spring Boot提供了一种方便的方式来读取配置。在本文中,我们将探讨如何在Spring Boot中使用Value和ConfigurationProperties注解来读取配置。 一、函数…...
)
pdf.js实现web h5预览pdf文件(兼容低版本浏览器)
注意 使用的是pdf.js 版本为 v2.16.105。因为新版本 兼容性不太好,部分手机预览不了,所以采用v2版本。 相关依赖 "canvas": "^2.11.2", "pdfjs-dist": "^2.16.105", "core-js-pure": "^3.37.…...

SSID简介
一、 SSID 概念定义 SSID(Service Set Identifier)即服务集标识符。它是无线网络中的一个重要标识,用于区分不同的无线网络。 相当于无线网络的名称,用于区分不同的无线网络。用户在众多可用网络中识别和选择特定网络的依据。通…...
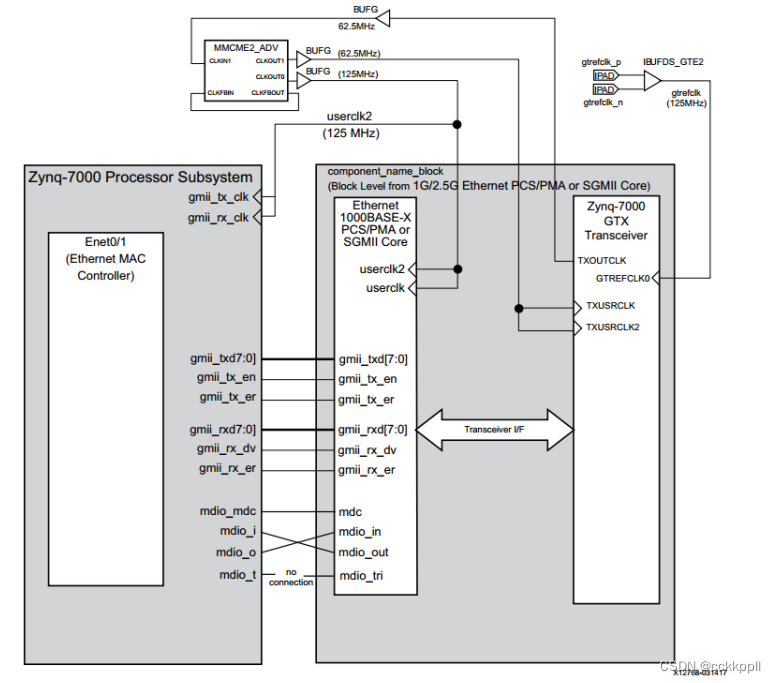
PS通过GTX实现SFP网络通信1
将 PS ENET1 的 GMII 接口和 MDIO 接口 通过 EMIO 方 式引出。在 PL 端将引出的 GMII 接口和 MDIO 接口与 IP 核 1G/2.5G Ethernet PCS/PMA or SGMII 连接, 1G/2.5G Ethernet PCS/PMA or SGMII 通过高速串行收发器 GTX 与 MIZ7035/7100 开发…...
前端面试项目细节重难点(已工作|做分享)(九)
面试官:请你讲讲你在工作中如何开发一个新需求,你的整个开发过程是什么样的? 答:仔细想想,我开发新需求的过程如下: (1)第一步:理解需求文档: 首先&#x…...
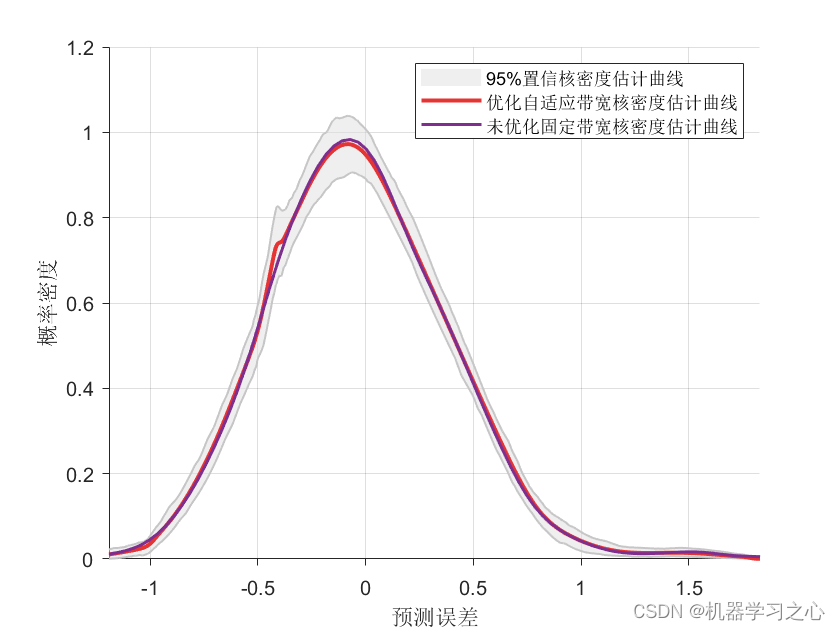
区间预测 | Matlab实现BP-ABKDE的BP神经网络自适应带宽核密度估计多变量回归区间预测
区间预测 | Matlab实现BP-ABKDE的BP神经网络自适应带宽核密度估计多变量回归区间预测 目录 区间预测 | Matlab实现BP-ABKDE的BP神经网络自适应带宽核密度估计多变量回归区间预测效果一览基本介绍程序设计参考资料 效果一览 基本介绍 1.Matlab实现BP-ABKDE的BP神经网络自适应带…...

抢占人工智能行业红利,前阿里巴巴产品专家带你15天入门AI产品经理
前言 当互联网行业巨头纷纷布局人工智能,国家将人工智能上升为国家战略,藤校核心课程涉足人工智能…人工智能领域蕴含着巨大潜力,早已成为业内共识。 面对极大的行业空缺,不少人都希望能抢占行业红利期,进入AI领域。…...
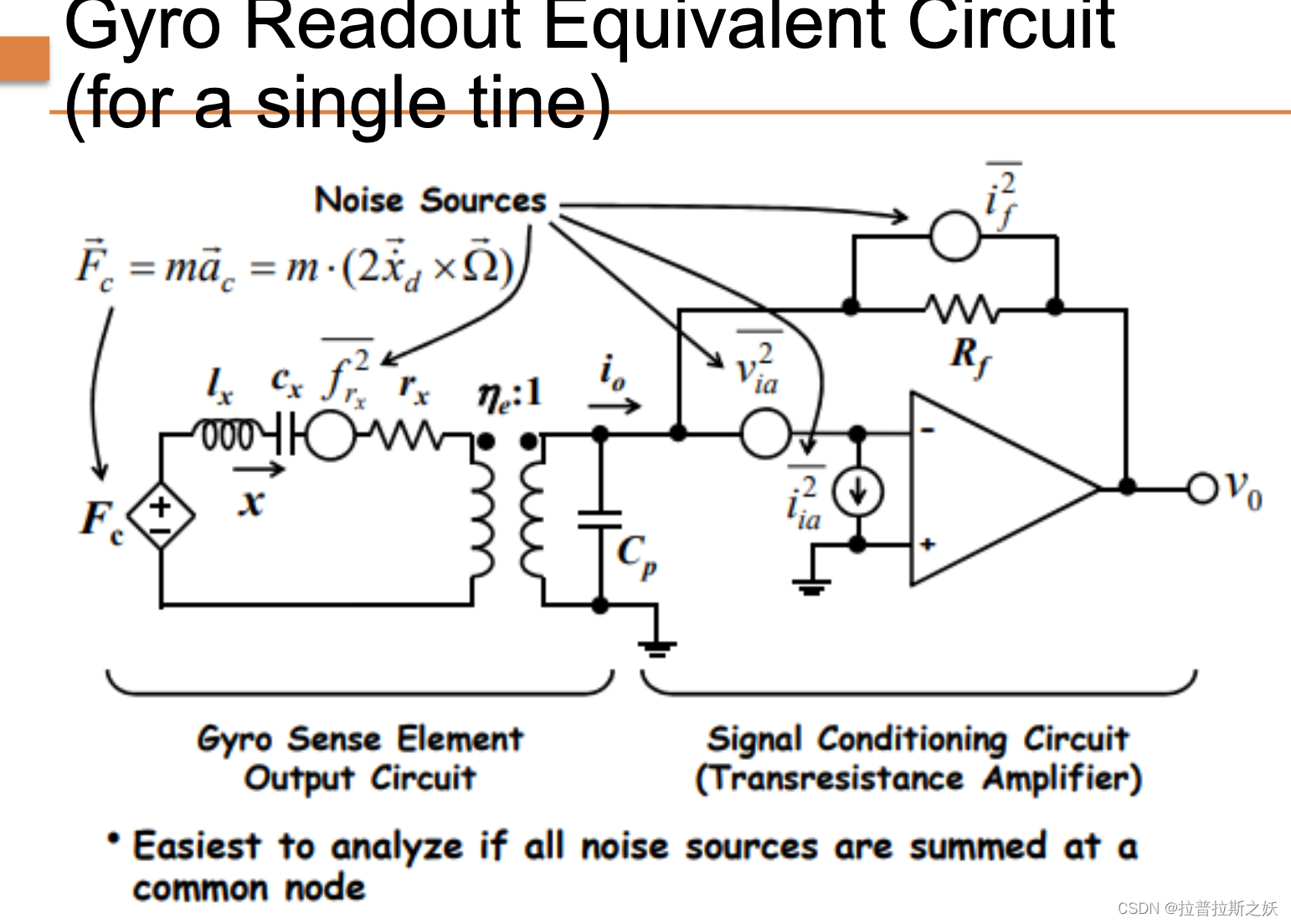
MEMS:Lecture 16 Gyros
陀螺仪原理 A classic spinning gyroscope measures the rotation rate by utilizing the conservation of angular momentum. 经典旋转陀螺仪通过利用角动量守恒来测量旋转速率。 Coriolis Effect and Coriolis Force 科里奥利效应是一种出现在旋转参考系中的现象。它描述了…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

C#中的CLR属性、依赖属性与附加属性
CLR属性的主要特征 封装性: 隐藏字段的实现细节 提供对字段的受控访问 访问控制: 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性: 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑: 可以…...
