5、斐波那契数列、跳台阶
题目: 斐波那契数列
描述:
大家都知道斐波那契数列,现在要求输入一个整数n,请你输出斐波那契数列的第n项。
n<=39
<?phpfunction Fibonacci($n)
{if($n<=0){$f1 = 0;}else if($n==1||$n==2){$f1 = 1;}else{$f1 = 1; $f2 = 1;while ($n-- > 2) {$f1 += $f2;$f2 = $f1-$f2;}}return $f1;
}
题目: 跳台阶
描述:
一只青蛙一次可以跳上1级台阶,也可以跳上2级。求该青蛙跳上一个n级的台阶总共有多少种跳法。
<?php
/*
解析:
在本体中只有两种跳法即,一阶或者两两阶
a.那么假定第一次跳的是一阶,那么剩下的是n-1个台阶,跳法是f(n-1);
b.假定第一次跳的是2阶,那么剩下的是n-2个台阶,跳法是f(n-2)
c.由a和b假设可以得出总跳法为: f(n) = f(n-1) + f(n-2)
d.然后通过实际的情况可以得出:只有一阶的时候 f(1) = 1 ,只有两阶的时候可以有 f(2) = 2
e.可以发现最终得出的是一个斐波那契数列:| 1, (n=1)
f(n) = | 2, (n=2)| f(n-1)+f(n-2) ,(n>2,n为整数)
采用迭代比递归效率高
*/
function jumpFloor($number)
{$value=0;if($number==1){$value = 1;}else if($number==2){$value = 2;}else{$f1 = 1; $f2 = 2;for($i=3;$i<=$number;$i++){$value = $f1+$f2;$f1 = $f2;$f2 = $value;}}return $value;
}
相关文章:

5、斐波那契数列、跳台阶
题目: 斐波那契数列 描述: 大家都知道斐波那契数列,现在要求输入一个整数n,请你输出斐波那契数列的第n项。 n<39 <?phpfunction Fibonacci($n) {if($n<0){$f1 0;}else if($n1||$n2){$f1 1;}else{$f1 1; $f2 1;whi…...
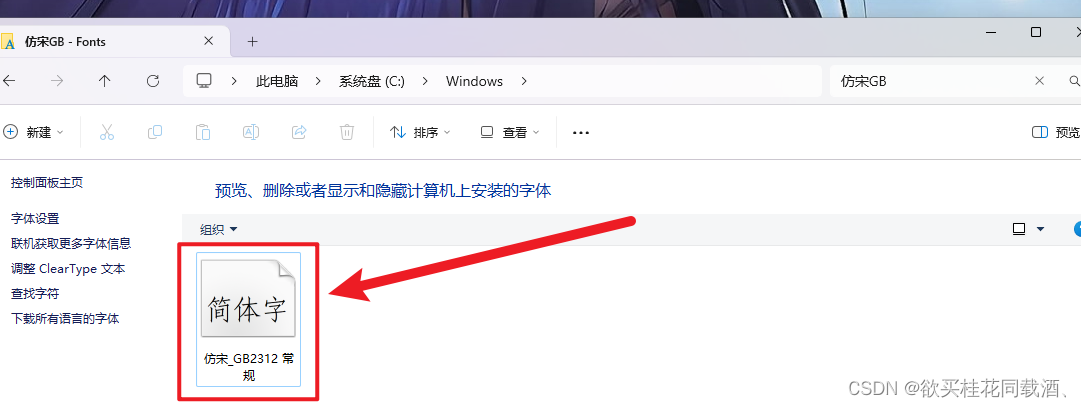
WPS相同字体但是部分文字样式不一样解决办法
如下图,在使用wps编辑文档的时候发现有些电脑的文字字体很奇怪,但是把鼠标移到这个文字的位置,发现它和其他正常文字的字体是一样的,都是仿宋_GB2312 正常电脑的文字如下图所示 打开C:\Windows找到Fonts这个文件夹 把仿宋_GB2312这…...

Scala运算符及流程控制
Scala运算符及流程控制 文章目录 Scala运算符及流程控制写在前面运算符算数运算符关系运算符赋值运算符逻辑运算符位运算符运算符本质 流程控制分支控制单分支双分支多分支 循环控制for循环while循环循环中断嵌套循环 写在前面 操作系统:Windows10JDK版本ÿ…...

Github 2024-06-10开源项目周报 Top15
根据Github Trendings的统计,本周(2024-06-10统计)共有15个项目上榜。根据开发语言中项目的数量,汇总情况如下: 开发语言项目数量Python项目8Jupyter Notebook项目2Go项目2C++项目1Shell项目1Lua项目1JavaScript项目1MDX项目1C项目1HTML项目1Python - 100天从新手到大师 创建…...
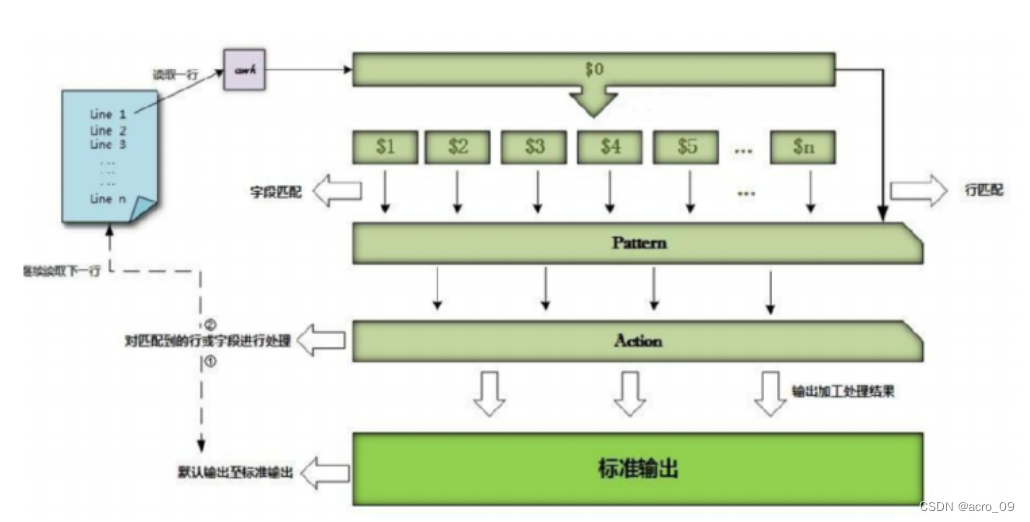
9. 文本三剑客之awk
文章目录 9.1 什么是awk9.2 awk命令格式9.3 awk执行流程9.4 行与列9.4.1 取行9.4.2 取列 9.1 什么是awk 虽然sed编辑器是非常方便自动修改文本文件的工具,但其也有自身的限制。通常你需要一个用来处理文件中的数据的更高级工具,它能提供一个类编程环境来…...

在vscode中调试,命令行出现错误信息ModuleNotFoundError: No module named ‘imp‘
在vscode中调试,命令行出现错误信息ModuleNotFoundError: No module named ‘imp’ 报错原因 VSCode的python扩展会使用debugpy库实现调试功能。在涉及qt组件加载时,debugpy的qt_loaders.py会尝试加载imp库。而在python3.12及以后的版本中,…...
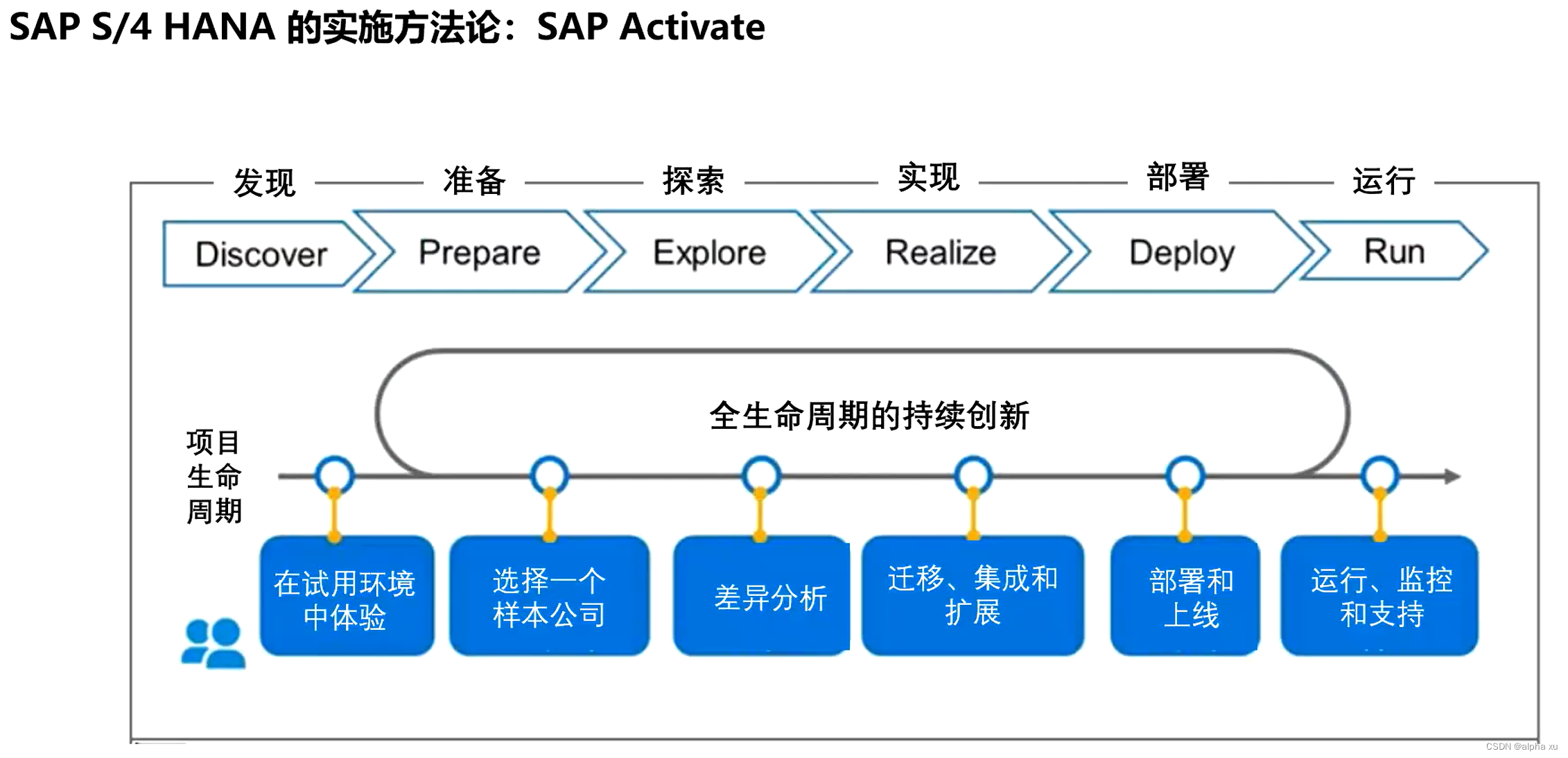
SAP实施方法论的变化
SAP 的实施方法论 ASAP,在SAP进入 S/4 HANA时,不知不觉改了意思。 原来叫Accelerate SAP,现在叫Activate SAP ,毕竟存量SAP太多,大部分用户并非象十多年前一样新实施SAP,而是在老的Sap R/3 ,MyS…...

phpstudy的安装dvwa
phpstudy安装dvwa 1. 下载phpstudy Windows版phpstudy下载 - 小皮面板(phpstudy) (xp.cn) 2. 搭建dvwa靶场 下载地址:https://github.com/ethicalhack3r/DVWA/archive/master.zip 将其放入www文件夹中 3. 修改配置文件 将\DVWA-master\config中config.inc.php…...

费曼的博士学位论文及下载
原始链接 PDF影印版下载 以前看《费曼物理学讲义》觉得最小作用原理部分讲得非常多、而且比较炫。现在知道原因了。 The principle of least action in quantum mechanics Richard Phillips Feynman(Princeton U. )May, 1942 74 pages Supervisor: John Archibald Wheeler…...

k8s学习--kubernetes服务自动伸缩之垂直伸缩(资源伸缩)VPA详细解释与安装
文章目录 前言VPA简介简单理解详细解释VPA的优缺点优点1.自动化资源管理2.资源优化3.性能和稳定性提升5.成本节约6.集成性和灵活性 缺点1.Pod 重启影响可用性2.与 HPA 冲突3.资源监控和推荐滞后:4.实现复杂度: 核心概念Resource Requests 和 Limits自动调…...

【OS】相关知识点收集
1 页面置换 页面置换算法是在计算机内存管理中用于决定哪些页面应该被替换出内存,以便为新的页面腾出空间的策略。以下是关于页面置换算法的详细回答,参考了多篇相关文章的信息。 1. 页面置换算法概述 页面置换算法主要应用于在存储体系当中ÿ…...
)
如何开发高效服务(C++ )
在 C 开发高效服务器时,常用的开发模式和设计模式能够帮助你构建高效、可扩展和可维护的服务器。以下是一些常见的模式和设计模式: 1. 并发和并行编程模型 1.1 Reactor 模式 Reactor 模式是一种事件驱动设计模式,广泛用于高性能服务器编程…...

STM32实现多级菜单界面显示
1、main函数中,while循环之前 MenuStruct menu[30] //定义多级菜单结构体数组{{0,0,0,1,show0}, //第一个元素表示索引号,第二个元素表示该按键按下后要返回的界面,第三个元素表示该按键按下后要切换的菜单条目界面,第四个元素…...

Qt事件处理和传递流程
事件系统的概述 事件的类型 Qt 支持多种事件类型,每种类型代表不同的用户交互或系统事件。常见的事件类型包括: 输入事件:如鼠标事件(QMouseEvent)、键盘事件(QKeyEvent)。窗口事件ÿ…...
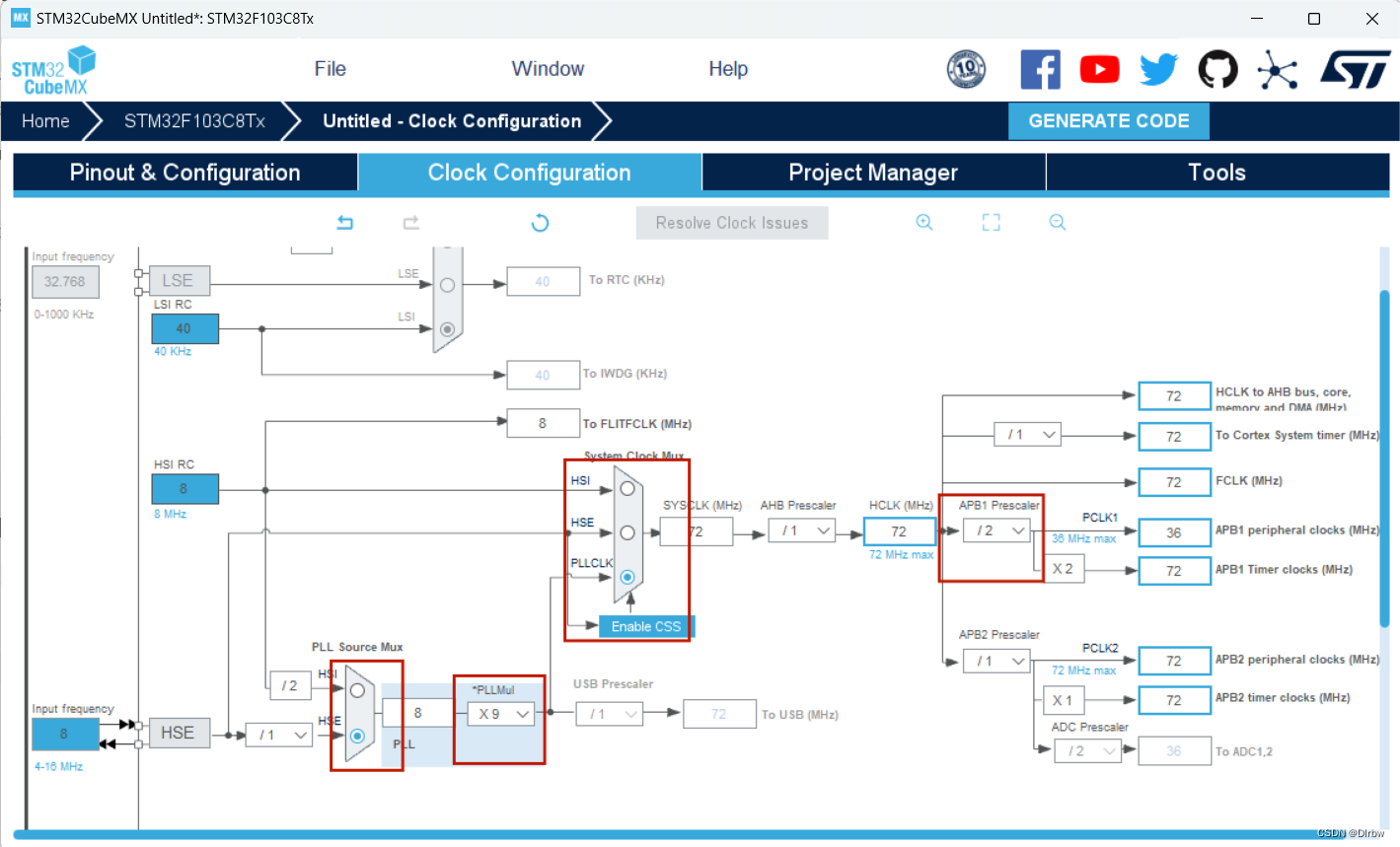
基于STM32移植U8g2图形库——OLED显示(HAL库)
文章目录 一、U8g2简介1、特点2、U8g2的使用步骤 二、I2C相关介绍1、I2C的基本原理2、I2C的时序协议 三、OLED屏的工作原理四、汉字点阵显示原理五、建立STM32CubeMX工程六、U8g2移植1、U8g2源码2、移植过程 七、代码编写1、参考博主实现的U82G的demo例程(1…...

C语言概述与历史
引言 C语言是一门历史悠久且影响深远的编程语言。它不仅为后继的许多编程语言奠定了基础,同时因其高效性和灵活性在系统编程和嵌入式开发领域得到了广泛应用。本篇文章将全面介绍C语言的起源与发展、设计目标与理念,以及C语言的标准演化历程,…...

钉钉Stream模式推送程序环境部署
python3.10版本需要openssl1.1.1及以上版本 参考链接:https://blog.csdn.net/weixin_42806458/article/details/110678710 wget https://www.openssl.org/source/openssl-1.1.1q.tar.gz unzip openssl-1.1.1q.tar.gz cd openssl-1.1.1q ./config --prefix/usr/loc…...
c# 二维图形绘制实践
1.等边三角形 1.1 概述 1.2 代码 using System; using System.Drawing; using System.Windows.Forms;public partial class TriangleForm : Form {public TriangleForm(){//InitializeComponent();// 确保窗体大小足够大,以容纳三角形 this.ClientSize new Siz…...

Nvidia TensorRT系列01-TensorRT的功能1
Nvidia TensorRT系列01-TensorRT的功能1 B站:肆十二-的个人空间-肆十二-个人主页-哔哩哔哩视频 (bilibili.com) 博客:肆十二-CSDN博客 问答:(10 封私信 / 72 条消息) 肆十二 - 知乎 (zhihu.com) C和Python API TensorRT的API同时支持C和Pyth…...

Vatee万腾平台:创新科技,助力企业腾飞
在全球化竞争日益激烈的今天,企业如何借助科技力量实现转型升级,已成为摆在众多企业家面前的重大课题。Vatee万腾平台凭借其卓越的创新科技和专业的服务能力,成为众多企业实现腾飞的得力助手。 一、创新科技,引领企业前行 Vatee万…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...

适应性Java用于现代 API:REST、GraphQL 和事件驱动
在快速发展的软件开发领域,REST、GraphQL 和事件驱动架构等新的 API 标准对于构建可扩展、高效的系统至关重要。Java 在现代 API 方面以其在企业应用中的稳定性而闻名,不断适应这些现代范式的需求。随着不断发展的生态系统,Java 在现代 API 方…...

关于easyexcel动态下拉选问题处理
前些日子突然碰到一个问题,说是客户的导入文件模版想支持部分导入内容的下拉选,于是我就找了easyexcel官网寻找解决方案,并没有找到合适的方案,没办法只能自己动手并分享出来,针对Java生成Excel下拉菜单时因选项过多导…...

SQL Server 触发器调用存储过程实现发送 HTTP 请求
文章目录 需求分析解决第 1 步:前置条件,启用 OLE 自动化方式 1:使用 SQL 实现启用 OLE 自动化方式 2:Sql Server 2005启动OLE自动化方式 3:Sql Server 2008启动OLE自动化第 2 步:创建存储过程第 3 步:创建触发器扩展 - 如何调试?第 1 步:登录 SQL Server 2008第 2 步…...

mac:大模型系列测试
0 MAC 前几天经过学生优惠以及国补17K入手了mac studio,然后这两天亲自测试其模型行运用能力如何,是否支持微调、推理速度等能力。下面进入正文。 1 mac 与 unsloth 按照下面的进行安装以及测试,是可以跑通文章里面的代码。训练速度也是很快的。 注意…...
